PID: Perbedaan antara revisi
Luckas-bot (bicara | kontrib) k bot Menambah: vi:Bộ điều khiển PID |
k v2.04b - Fixed using Wikipedia:ProyekWiki Cek Wikipedia (Subbagian dengan huruf tebal) |
||
| (31 revisi perantara oleh 19 pengguna tidak ditampilkan) | |||
| Baris 1: | Baris 1: | ||
[[Berkas:Pid-feedback-nct-int-correct.png| |
[[Berkas:Pid-feedback-nct-int-correct.png|jmpl|Blok diagram dari kontroler PID]] |
||
'''PID''' (dari singkatan bahasa [[Inggris]]: ''Proportional–Integral–Derivative controller'') merupakan kontroler |
'''Kontroler PID''' (dari singkatan bahasa [[Inggris]]: ''Proportional–Integral–Derivative controller'') merupakan kontroler [[mekanisme umpan balik]] yang biasanya dipakai pada [[sistem kontrol industri]]. Sebuah kontroler PID secara kontinu menghitung ''nilai kesalahan'' sebagai beda antara [[Setpoint (sistem kontrol)|setpoint]] yang diinginkan dan [[variabel proses]] terukur. Kontroler mencoba untuk meminimalkan nilai kesalahan setiap waktu dengan penyetelan ''variabel kontrol'', seperti posisi [[keran kontrol]], [[damper (aliran)|damper]], atau daya pada elemen pemanas, ke nilai baru yang ditentukan oleh jumlahan: |
||
:<math>u(t) = K_p e(t) + K_i \int_{0}^{t}e(\tau)d\tau + K_d \frac{de(t)}{dt}</math> |
|||
Komponen kontrol PID ini terdiri dari tiga jenis yaitu '''Proportional, Integratif''' dan '''Derivatif'''. Ketiganya dapat dipakai bersamaan maupun sendiri-sendiri tergantung dari respon yang kita inginkan terhadap suatu plant. |
|||
dengan <math>K_p</math>, <math>K_i</math>, and <math>K_d</math>, semuanya positif, menandakan koefisien untuk term [[kontrol proporsional|proporsional]], [[integral]], dan [[derivatif]], secara berurutan (atau ''P,'' ''I,'' dan ''D''). Pada model ini, |
|||
1.'''Kontrol Proporsional''' |
|||
* ''P'' bertanggung jawab untuk nilai kesalahan saat ini. Contohnya, jika nilai kesalahan besar dan positif, maka keluaran kontrol juga besar dan positif. |
|||
* ''I'' bertanggung jawab untuk nilai kesalahan sebelumnya. Contoh, jika keluaran saat ini kurang besar, maka kesalahan akan terakumulasi terus menerus, dan kontroler akan merespon dengan keluaran lebih tinggi. |
|||
* ''D'' bertanggung jawab untuk kemungkinan nilai kesalahan mendatang, berdasarkan pada rate perubahan tiap waktu.<ref>{{cite web | url = http://www.eolss.net/ebooks/Sample%20Chapters/C18/E6-43-03-03.pdf | title = PID Control | last = Araki | first = M. | ref = harv }}</ref> |
|||
Karena kontroler PID hanya mengandalkan variabel proses terukur, bukan pengetahuan mengenai prosesnya, maka dapat secara luas digunakan.<ref name="ben93p48" /> Dengan penyesuaian (''tuning'') ketiga parameter model, kontroler PID dapat memenuhi kebutuhan proses. Respon kontroler dapat dijelaskan dengan bagaimana responnya terhadap kesalahan, besarnya [[overshoot (sinyal)|overshoot]] dari setpoint, dan derajat osilasi sistem. penggunaan algoritme PID tidak menjamin [[kontrol optimum]] sistem atau bahkan [[kriteria stabilitas Nyquist|kestabilannya]]. |
|||
Kontrol P jika G(s) = kp, dengan k adalah konstanta. Jika u = G(s) • e maka |
|||
u = Kp • e |
|||
dengan Kp adalah Konstanta Proporsional. Kp berlaku sebagai Gain (penguat) saja tanpa memberikan efek dinamik kepada kinerja kontroler. |
|||
Penggunaan kontrol P memiliki berbagai keterbatasan karena sifat kontrol yang tidak dinamik ini. Walaupun demikian dalam aplikasi-aplikasi dasar yang sederhana kontrol P ini cukup mampu untuk memperbaiki respon transien khususnya rise time dan settling time. |
|||
Beberapa aplikasi mungkin hanya menggunakan satu atau dua term untuk memberikan kontrol sistem yang sesuai. Hal ini dapat dicapai dengan mengontrol parameter yang lain menjadi nol. Kontroler PID dapat menjadi kontroler PI, PD, P atau I tergantung aksi apa yang digunakan. Kontroler PI biasanya adalah kontroler paling umum. |
|||
2.'''Kontrol Integratif''' |
|||
Untuk sistem [[waktu diskrit]], sering digunakan PSD atau '''proportional-summation-difference'''.<ref>{{Cite web |url=https://www.kirp.chtf.stuba.sk/pc11/data/papers/077.pdf |title=Veselý, V., Rosinová, D.: Robust PSD Controller Design, Editors: Fikar, M., Kvasnica, M., In Proceedings of the 18th International Conference on Process Control, Tatranská Lomnica, Slowakia, 565–570, 2011 |access-date=2016-04-26 |archive-date=2016-03-04 |archive-url=https://web.archive.org/web/20160304230225/https://www.kirp.chtf.stuba.sk/pc11/data/papers/077.pdf |dead-url=yes }}</ref> |
|||
Jika G(s) adalah kontrol I maka u dapat dinyatakan sebagai |
|||
<math>u(t)=[integral e(t)dT]Ki</math> |
|||
dengan Ki adalah konstanta Integral, dan dari persamaan diatas, G(s) dapat dinyatakan sebagai |
|||
<math>u=Kd.[delta e/delta t]</math> |
|||
Jika e(T) mendekati konstan (bukan nol) maka u(t) akan menjadi sangat besar sehingga diharapkan dapat memperbaiki error. Jika e(T) mendekati nol maka efek kontrol I ini semakin kecil. Kontrol I dapat memperbaiki sekaligus menghilangkan respon steady-state, namun pemilihan Ki yang tidak tepat dapat menyebabkan respon transien yang tinggi sehingga dapat menyebabkan ketidakstabilan sistem. Pemilihan Ki yang sangat tinggi justru dapat menyebabkan output berosilasi karena menambah orde sistem |
|||
== Teori kontroler PID == |
|||
3.'''Kontrol Derivatif''' |
|||
Skema kontrol PID dinamai dari ketiga term pengendalinya, yang kemudian dijumlahkan menjadi variabel manipulasi. Term proporsional, integral, dan derivatif dijumlahkan untuk menghitung keluaran kontroler PID. Dengan mendefinisikan <math>u(t)</math> sebagai keluaran kontroler, bentuk akhir dari algoritme PID adalah: |
|||
:<math>\mathrm{u}(t)=\mathrm{P}(t)=K_p{e(t)} + K_{i}\int_{0}^{t}{e(\tau)}\,{d\tau} + K_{d}\frac{de(t)}{dt}</math> |
|||
Sinyal kontrol u yang dihasilkan oleh kontrol D dapat dinyatakan sebagai |
|||
<math>G(s)=s.Kd</math> |
|||
Dari persamaan di atas, nampak bahwa sifat dari kontrol D ini dalam konteks "kecepatan" atau rate dari error. Dengan sifat ini ia dapat digunakan untuk memperbaiki respon transien dengan memprediksi error yang akan terjadi. Kontrol Derivative hanya berubah saat ada perubahan error sehingga saat error statis kontrol ini tidak akan bereaksi, hal ini pula yang menyebabkan kontroler Derivative tidak dapat dipakai sendiri |
|||
dengan |
|||
{{elektronika-stub}} |
|||
: <math>K_p</math>: ''Gain'' proporsional, parameter tuning |
|||
: <math>K_i</math>: ''Gain'' Integral, parameter tuning |
|||
: <math>K_d</math>: ''Gain'' Derivatif, parameter tuning |
|||
: <math>e</math>: Error <math> = Y_{sp}-Y_m </math> |
|||
: <math>Y_{sp}</math>: Setpoint |
|||
: <math>Y_m</math>: Variabel proses |
|||
: <math>t</math>: Waktu |
|||
: <math>\tau</math>: Variabel integrasi; nilainya diambil dari waktu nol sampai <math>t</math>. |
|||
Transfer fungsi dalam bentuk [[Transformasi Laplace|Domain Laplace]] kontroler PID adalah |
|||
:<math>L(s)=K_p + K_{i}/s + K_{d}s</math> |
|||
dengan |
|||
: <math>s</math>: frekuensi bilangan kompleks |
|||
=== Term Proporsional === |
|||
[[Berkas:PID varyingP.jpg|ka|jmpl|320px|Plot Y vs waktu, untuk 3 nilai K<sub>p</sub> (K<sub>i</sub> dan K<sub>d</sub> dijaga konstan)]] |
|||
Term proporsional akan menghasilkan nilai keluaran yang berbanding lurus dengan nilai kesalahan. Responnya dapat diatur dengan mengalikan kesalahan (error) dengan konstanta ''K<sub>p</sub>'', disebut konstanta ''gain'' proporsional atau ''gain'' kontroler. |
|||
Term proporsional dirumuskan: |
|||
:<math>P_{\mathrm{out}}=K_p\,{e(t)}</math> |
|||
:<math>P_{\mathrm{out}}=K_p\,(Y_{sp}-Y_m)</math> |
|||
Gain yang besar menghasilkan perubahan yang besar pada keluaran untuk suatu nilai kesalahan tertentu. Namun, jika gain terlalu besar, sistem akan membutuhkan waktu yang cukup lama untuk mencapai kondisi ''steady-state'' (lihat bagian [[#Loop tuning|loop tuning]]). Sebaliknya, gain yang bernilai kecil maka respon keluaran juga kecil, sehingga kontroler menjadi kurang responsif/sensitif, hal ini akan mengakibatkan respon kontroler akan lebih lambat jika mendapatkan gangguan.. |
|||
=== Term integral === |
|||
[[Berkas:Change with Ki.png|ka|jmpl|320px|Plot Y vs waktu, untuk 3 nilai K<sub>i</sub> (K<sub>p</sub> dan K<sub>d</sub> dijaga konstan)]] |
|||
Peranan dari term integral berbanding lurus dengan besar dan lamanya error. [[Integral]] dalam kontroler PID adalah jumlahan error setiap waktu dan mengakumulasi offset yang sebelumnya telah dikoreksi. Error terakumulasi dikalikan dengan ''gain'' integral (<math>K_i</math>) dan menjadi keluaran kontroler. |
|||
Term integral dirumuskan dengan: |
|||
: <math>I_{\mathrm{out}}=K_{i}\int_{0}^{t}{e(\tau)}\,{d\tau}</math> |
|||
Term integral mempercepat perpindahan proses menuju setpoint dan menghilangkan ''steady-state error'' yang muncul pada kontroler proporsional. Namun, karena integral merespon terhadap error terakumulasi dari sebelumnya, maka dapat menyebabkan [[Overshoot (sinyal)|overshoot]]. |
|||
=== Term derivatif === |
|||
[[Berkas:Change with Kd.png|ka|jmpl|320px|Plot Y vs waktu, untuk 3 nilai K<sub>d</sub> (K<sub>p</sub> dan K<sub>i</sub> dijaga konstan)]] |
|||
[[Turunan]] error pada proses dihitung dengan menentukan kemiringan error setiap waktu dan mengalikan perubahan tiap waktu dengan ''gain'' derivatif ''K<sub>d</sub>''. |
|||
Term derivatif dirumuskan dengan: |
|||
:<math>D_{\mathrm{out}}=K_d\frac{de(t)}{dt}</math> |
|||
Aksi derivatif memprediksi perilaku sistem dan kemudian memperbaiki waktu tinggal dan stabilitas sistem.<ref>{{cite web |url=http://ctms.engin.umich.edu/CTMS/index.php?example=Introduction§ion=ControlPID |title=Introduction: PID Controller Design |publisher=University of Michigan}}</ref><ref>{{cite journal |title=PID without a PhD |url=http://igor.chudov.com/manuals/Servo-Tuning/PID-without-a-PhD.pdf |publisher=EE Times-India |date=October 2000 |author=Tim Wescott}}</ref> Aksi derivatif jarang digunakan pada industri - diperkirakan hanya 25% kontroler<ref name="IEEE_PID_05" /> - karena akibatnya pada stabilitas sistem pada aplikasi dunia nyata.<ref name="IEEE_PID_05" /> |
|||
=== Tunning nilai Kp, Ki dan Kd === |
|||
Ada beberapa cara untuk menentukan nilai Kp, Ki, Kd. Salah satunya adalah dengan cara tunning nilainya satu persatu. dimulai dengan nilai Kp (''Gain'' proporsional) terlebih dahulu, hal ini dikarenakan kita perlu mencari respon sistem yang paling cepat dengan cara meminimalkan nilai ''rise time'', jangan memberikan nilai Kp terlalu besar atau terlalu kecil. Setelah respon dirasa cukup tepat hal selanjutnya yang dapat dilakukan adalah dengan memberikan nilai pada Kd (''Gain'' Derivatif), hal ini bertujuan untuk mengecilkan nilai amplitudo sehingga [[osilasi]] dapat diredam atau bahkan dihilangkan. Kemudian proses terakhir pada ''tunning'' nilai ''Gain'' adalah dengan mencari nilai Ki (''Gain'' Integral), ''tunning'' Ki diperlukan jika kondisi sistem memiliki ''steady state error,'' yakni terjadi selisih antara nilai ''set point'' dengan nilai sistem saat mencapai kondisi ''steady state.'' |
|||
Video tutorial tunning PID.<ref>{{Citation|last=Northwestern Robotics|title=Empirical PID gain tuning (Kevin Lynch)|date=2015-12-07|url=https://www.youtube.com/watch?v=uXnDwojRb1g|accessdate=2018-08-30}}</ref> |
|||
=== Referensi === |
|||
{{reflist}} |
|||
== Pranala luar == |
|||
* [http://reference.wolfram.com/mathematica/ref/PIDTune.html PID tuning using Mathematica] |
|||
* [http://www.eurotherm.com/temperature-control/principles-of-pid-control-and-tuning Principles of PID Control and Tuning] |
|||
* [http://www.eurotherm.com/temperature-control/pid-control-made-easy Introduction to the key terms associated with PID Temperature Control] |
|||
=== Tutorial PID === |
|||
* [http://www.pidlab.com/ PID tutorial, free PID tuning tools, advanced PID control schemes, on-line PID simulators] |
|||
* [http://electronicdesign.com/analog/whats-all-p-i-d-stuff-anyhow What's All This P-I-D Stuff, Anyhow?] Article in Electronic Design |
|||
* [http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.154.240&rep=rep1&type=pdf Shows how to build a PID controller with basic electronic components] (pg. 22) |
|||
* [http://www.che.utexas.edu/course/che360/Process_Tuner.html Online PID Tuning applet from University of Texas Control Group] |
|||
* [http://www.mathworks.com/discovery/pid-control.html PID Control with MATLAB and Simulink] |
|||
* [http://www.postreh.com/vmichal/papers/PID-Radio.pdf PID with single Operational Amplifier] |
|||
* [http://www.controlguru.com/pages/table.html Proven Methods and Best Practices for PID Control] |
|||
* [http://www.eurotherm.com/temperature-control/principles-of-pid-control-and-tuning Principles of PID Control and Tuning] |
|||
* {{citation |url=http://www.embedded.com/story/OEG20020726S0044 |archiveurl=https://web.archive.org/web/20100209125831/http://embedded.com/story/OEG20020726S0044 |archivedate=2010-02-09 |author=Michael Barr |title=Introduction to Closed-Loop Control |publisher=Embedded Systems Programming |date=2002-07-30}} |
|||
* {{cite web |url=http://saba.kntu.ac.ir/eecd/pcl/download/PIDtutorial.pdf |title=PID Controller Tuning: A Short Tutorial |author=Jinghua Zhong, Mechanical Engineering, Purdue University |date=Spring 2006 |accessdate=2013-12-04 |archive-date=2015-04-21 |archive-url=https://web.archive.org/web/20150421081758/http://saba.kntu.ac.ir/eecd/pcl/download/PIDtutorial.pdf |dead-url=yes }} |
|||
* [http://vivekbose.com/introduction-to-pid-controller-with-detailed-ppipd-pd-control Introduction to P,PI,PD & PID Controller with MATLAB] |
|||
[[Kategori:Instrumentasi]] |
[[Kategori:Instrumentasi]] |
||
[[Kategori:Teknologi]] |
[[Kategori:Teknologi]] |
||
[[ar:عنصر تحكم تناسبي تكاملي تفاضلي]] |
|||
{{elektronika-stub}} |
|||
[[bg:PID контролер]] |
|||
[[ca:Controlador PID]] |
|||
[[cs:PID regulátor]] |
|||
[[de:Regler#PID-Regler]] |
|||
[[en:PID controller]] |
|||
[[es:Proporcional integral derivativo]] |
|||
[[fi:PID-säädin]] |
|||
[[fr:Régulateur PID]] |
|||
[[hu:PID szabályozó]] |
|||
[[it:Controllori PID]] |
|||
[[ja:PID制御]] |
|||
[[ko:PID 제어기]] |
|||
[[lt:PID reguliatorius]] |
|||
[[nl:PID-regelaar]] |
|||
[[no:PID-regulator]] |
|||
[[pl:Regulator PID]] |
|||
[[ru:ПИД-регулятор]] |
|||
[[sk:PID regulátor]] |
|||
[[sv:PID-regulator]] |
|||
[[th:ระบบควบคุมพีไอดี]] |
|||
[[vi:Bộ điều khiển PID]] |
|||
[[zh:PID控制器]] |
|||
Revisi terkini sejak 28 Juni 2021 03.04

Kontroler PID (dari singkatan bahasa Inggris: Proportional–Integral–Derivative controller) merupakan kontroler mekanisme umpan balik yang biasanya dipakai pada sistem kontrol industri. Sebuah kontroler PID secara kontinu menghitung nilai kesalahan sebagai beda antara setpoint yang diinginkan dan variabel proses terukur. Kontroler mencoba untuk meminimalkan nilai kesalahan setiap waktu dengan penyetelan variabel kontrol, seperti posisi keran kontrol, damper, atau daya pada elemen pemanas, ke nilai baru yang ditentukan oleh jumlahan:
dengan , , and , semuanya positif, menandakan koefisien untuk term proporsional, integral, dan derivatif, secara berurutan (atau P, I, dan D). Pada model ini,
- P bertanggung jawab untuk nilai kesalahan saat ini. Contohnya, jika nilai kesalahan besar dan positif, maka keluaran kontrol juga besar dan positif.
- I bertanggung jawab untuk nilai kesalahan sebelumnya. Contoh, jika keluaran saat ini kurang besar, maka kesalahan akan terakumulasi terus menerus, dan kontroler akan merespon dengan keluaran lebih tinggi.
- D bertanggung jawab untuk kemungkinan nilai kesalahan mendatang, berdasarkan pada rate perubahan tiap waktu.[1]
Karena kontroler PID hanya mengandalkan variabel proses terukur, bukan pengetahuan mengenai prosesnya, maka dapat secara luas digunakan.[2] Dengan penyesuaian (tuning) ketiga parameter model, kontroler PID dapat memenuhi kebutuhan proses. Respon kontroler dapat dijelaskan dengan bagaimana responnya terhadap kesalahan, besarnya overshoot dari setpoint, dan derajat osilasi sistem. penggunaan algoritme PID tidak menjamin kontrol optimum sistem atau bahkan kestabilannya.
Beberapa aplikasi mungkin hanya menggunakan satu atau dua term untuk memberikan kontrol sistem yang sesuai. Hal ini dapat dicapai dengan mengontrol parameter yang lain menjadi nol. Kontroler PID dapat menjadi kontroler PI, PD, P atau I tergantung aksi apa yang digunakan. Kontroler PI biasanya adalah kontroler paling umum.
Untuk sistem waktu diskrit, sering digunakan PSD atau proportional-summation-difference.[3]
Teori kontroler PID
[sunting | sunting sumber]Skema kontrol PID dinamai dari ketiga term pengendalinya, yang kemudian dijumlahkan menjadi variabel manipulasi. Term proporsional, integral, dan derivatif dijumlahkan untuk menghitung keluaran kontroler PID. Dengan mendefinisikan sebagai keluaran kontroler, bentuk akhir dari algoritme PID adalah:
dengan
- : Gain proporsional, parameter tuning
- : Gain Integral, parameter tuning
- : Gain Derivatif, parameter tuning
- : Error
- : Setpoint
- : Variabel proses
- : Waktu
- : Variabel integrasi; nilainya diambil dari waktu nol sampai .
Transfer fungsi dalam bentuk Domain Laplace kontroler PID adalah
dengan
- : frekuensi bilangan kompleks
Term Proporsional
[sunting | sunting sumber]
Term proporsional akan menghasilkan nilai keluaran yang berbanding lurus dengan nilai kesalahan. Responnya dapat diatur dengan mengalikan kesalahan (error) dengan konstanta Kp, disebut konstanta gain proporsional atau gain kontroler.
Term proporsional dirumuskan:
Gain yang besar menghasilkan perubahan yang besar pada keluaran untuk suatu nilai kesalahan tertentu. Namun, jika gain terlalu besar, sistem akan membutuhkan waktu yang cukup lama untuk mencapai kondisi steady-state (lihat bagian loop tuning). Sebaliknya, gain yang bernilai kecil maka respon keluaran juga kecil, sehingga kontroler menjadi kurang responsif/sensitif, hal ini akan mengakibatkan respon kontroler akan lebih lambat jika mendapatkan gangguan..
Term integral
[sunting | sunting sumber]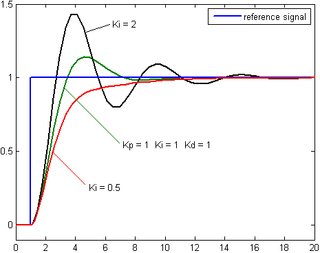
Peranan dari term integral berbanding lurus dengan besar dan lamanya error. Integral dalam kontroler PID adalah jumlahan error setiap waktu dan mengakumulasi offset yang sebelumnya telah dikoreksi. Error terakumulasi dikalikan dengan gain integral () dan menjadi keluaran kontroler.
Term integral dirumuskan dengan:
Term integral mempercepat perpindahan proses menuju setpoint dan menghilangkan steady-state error yang muncul pada kontroler proporsional. Namun, karena integral merespon terhadap error terakumulasi dari sebelumnya, maka dapat menyebabkan overshoot.
Term derivatif
[sunting | sunting sumber]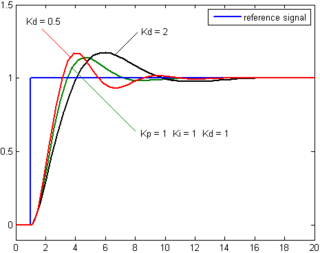
Turunan error pada proses dihitung dengan menentukan kemiringan error setiap waktu dan mengalikan perubahan tiap waktu dengan gain derivatif Kd.
Term derivatif dirumuskan dengan:
Aksi derivatif memprediksi perilaku sistem dan kemudian memperbaiki waktu tinggal dan stabilitas sistem.[4][5] Aksi derivatif jarang digunakan pada industri - diperkirakan hanya 25% kontroler[6] - karena akibatnya pada stabilitas sistem pada aplikasi dunia nyata.[6]
Tunning nilai Kp, Ki dan Kd
[sunting | sunting sumber]Ada beberapa cara untuk menentukan nilai Kp, Ki, Kd. Salah satunya adalah dengan cara tunning nilainya satu persatu. dimulai dengan nilai Kp (Gain proporsional) terlebih dahulu, hal ini dikarenakan kita perlu mencari respon sistem yang paling cepat dengan cara meminimalkan nilai rise time, jangan memberikan nilai Kp terlalu besar atau terlalu kecil. Setelah respon dirasa cukup tepat hal selanjutnya yang dapat dilakukan adalah dengan memberikan nilai pada Kd (Gain Derivatif), hal ini bertujuan untuk mengecilkan nilai amplitudo sehingga osilasi dapat diredam atau bahkan dihilangkan. Kemudian proses terakhir pada tunning nilai Gain adalah dengan mencari nilai Ki (Gain Integral), tunning Ki diperlukan jika kondisi sistem memiliki steady state error, yakni terjadi selisih antara nilai set point dengan nilai sistem saat mencapai kondisi steady state.
Video tutorial tunning PID.[7]
Referensi
[sunting | sunting sumber]- ^ Araki, M. "PID Control" (PDF).
- ^ Kesalahan pengutipan: Tag
<ref>tidak sah; tidak ditemukan teks untuk ref bernamaben93p48 - ^ "Veselý, V., Rosinová, D.: Robust PSD Controller Design, Editors: Fikar, M., Kvasnica, M., In Proceedings of the 18th International Conference on Process Control, Tatranská Lomnica, Slowakia, 565–570, 2011" (PDF). Diarsipkan dari versi asli (PDF) tanggal 2016-03-04. Diakses tanggal 2016-04-26.
- ^ "Introduction: PID Controller Design". University of Michigan.
- ^ Tim Wescott (October 2000). "PID without a PhD" (PDF). EE Times-India.
- ^ a b Kesalahan pengutipan: Tag
<ref>tidak sah; tidak ditemukan teks untuk ref bernamaIEEE_PID_05 - ^ Northwestern Robotics (2015-12-07), Empirical PID gain tuning (Kevin Lynch), diakses tanggal 2018-08-30
Pranala luar
[sunting | sunting sumber]- PID tuning using Mathematica
- Principles of PID Control and Tuning
- Introduction to the key terms associated with PID Temperature Control
Tutorial PID
[sunting | sunting sumber]- PID tutorial, free PID tuning tools, advanced PID control schemes, on-line PID simulators
- What's All This P-I-D Stuff, Anyhow? Article in Electronic Design
- Shows how to build a PID controller with basic electronic components (pg. 22)
- Online PID Tuning applet from University of Texas Control Group
- PID Control with MATLAB and Simulink
- PID with single Operational Amplifier
- Proven Methods and Best Practices for PID Control
- Principles of PID Control and Tuning
- Michael Barr (2002-07-30), Introduction to Closed-Loop Control, Embedded Systems Programming, diarsipkan dari versi asli tanggal 2010-02-09
- Jinghua Zhong, Mechanical Engineering, Purdue University (Spring 2006). "PID Controller Tuning: A Short Tutorial" (PDF). Diarsipkan dari versi asli (PDF) tanggal 2015-04-21. Diakses tanggal 2013-12-04.
- Introduction to P,PI,PD & PID Controller with MATLAB


















