Teorema Bayes: Perbedaan antara revisi
k Bot: Perubahan kosmetika |
→Pengenalan: Penambahan penjelasan mengapa peluang tidak mungkin nilainya mencapai 1 Tag: Suntingan perangkat seluler Suntingan peramban seluler |
||
| (9 revisi perantara oleh 6 pengguna tidak ditampilkan) | |||
| Baris 1: | Baris 1: | ||
[[Berkas:Bayes'_Theorem_MMB_01.jpg|jmpl|ka|200px|Perumusan singkat Teorema Bayes]] |
[[Berkas:Bayes'_Theorem_MMB_01.jpg|jmpl|ka|200px|Perumusan singkat Teorema Bayes]] |
||
Dalam [[teori probabilitas]] dan [[statistika]], |
|||
'''teorema Bayes''' adalah sebuah [[teorema]] dengan dua penafsiran berbeda. Dalam ''penafsiran Bayes'', teorema ini menyatakan seberapa jauh derajat kepercayaan subjektif seseorang harus berubah secara rasional ketika ada petunjuk atau informasi baru. Sebagai contoh di malam hari sebelum tidur, kita percaya secara subjektif bahwa besok akan cerah dan peluang hujan hanya 10%. Besok paginya kita bangun tidur dan mendengar berita ramalan cuaca bahwa sedang terjadi hujan lebat di berbagai kota maka kepercayaan subjektif kita berubah dan menaksir bahwa peluang hari ini akan hujan adalah 50%. Dalam ''penafsiran frekuentis'' teorema ini menjelaskan representasi invers probabilitas dua kejadian. Teorema ini merupakan dasar dari [[statistika Bayes]] dan memiliki penerapan dalam [[sains]], [[rekayasa]], [[ilmu ekonomi]] (terutama ilmu ekonomi mikro), [[teori permainan]], [[kedokteran]] dan [[hukum]]. Penerapan teorema Bayes untuk memperbarui kepercayaan dinamakan inferens Bayes. |
|||
== Pengenalan == |
== Pengenalan == |
||
Contoh singkat dari teorema bayes: |
|||
| ⚫ | Misalkan kawan Anda bercerita dia bercakap-cakap akrab dengan seseorang lain di atas kereta api. Tanpa informasi tambahan, [[peluang (matematika)|peluang]] dia bercakap-cakap dengan perempuan adalah 50%. Sekarang misalkan kawan Anda menyebut bahwa orang lain di atas kereta api itu berambut panjang. Dari keterangan baru ini tampaknya lebih |
||
| ⚫ | Misalkan kawan Anda bercerita dia bercakap-cakap akrab dengan seseorang lain di atas kereta api. Tanpa informasi tambahan, [[peluang (matematika)|peluang]] dia bercakap-cakap dengan perempuan adalah 50%. Sekarang misalkan kawan Anda menyebut bahwa orang lain di atas kereta api itu berambut panjang. Dari keterangan baru ini tampaknya lebih boleh jadi kawan Anda bercakap-cakap dengan perempuan, karena orang berambut panjang biasanya wanita. Teorema Bayes dapat digunakan untuk menghitung besarnya peluang bahwa kawan Anda berbicara dengan seorang wanita, bila diketahui berapa peluang seorang wanita berambut panjang. |
||
Misalkan: |
Misalkan: |
||
| Baris 13: | Baris 16: | ||
:<math>P(W) = 0,5</math> |
:<math>P(W) = 0,5</math> |
||
Misalkan juga |
Misalkan juga diketahui 75 persen wanita berambut panjang. Ini berarti bila kita mengetahui bahwa seseorang adalah wanita, peluangnya berambut panjang adalah 0,75. Kita melambangkannya sebagai: |
||
:<math>P(L|W) = 0,75</math> |
:<math>P(L|W) = 0,75</math> |
||
| Baris 23: | Baris 26: | ||
Tujuan kita adalah menghitung peluang seseorang itu adalah wanita bila diketahui dia berambut panjang, atau dalam notasi yang kita gunakan, ''P''(''W''|''L''). Menggunakan teorema Bayes, kita mendapatkan: |
Tujuan kita adalah menghitung peluang seseorang itu adalah wanita bila diketahui dia berambut panjang, atau dalam notasi yang kita gunakan, ''P''(''W''|''L''). Menggunakan teorema Bayes, kita mendapatkan: |
||
:<math> P(W|L) = \frac{P(L|W)P(W)}{P(L)}</math> |
|||
:<math>P(W|L) = \frac{P(L|W) P(W)}{P(L|W)P(W) + P(L|M)P(M)}</math> |
:<math>P(W|L) = \frac{P(L|W) P(W)}{P(L|W)P(W) + P(L|M)P(M)}</math> |
||
Di sini kita menggunakan [[aturan peluang total]]. Dengan memasukkan nilai-nilai peluang yang diketahui ke dalam rumus di atas, kita mendapatkan peluang seseorang itu wanita bila diketahui dia berambut panjang adalah 0,714. Angka ini sesuai dengan intuisi awal kita, bahwa peluang kawan kita itu bercakap-cakap dengan wanita meningkat. |
Di sini kita menggunakan [[aturan peluang total]]. Dengan memasukkan nilai-nilai peluang yang diketahui ke dalam rumus di atas, kita mendapatkan peluang seseorang itu wanita bila diketahui dia berambut panjang adalah 0,714. Angka ini sesuai dengan intuisi awal kita, bahwa peluang kawan kita itu bercakap-cakap dengan wanita meningkat. Walaupun demikian, peluangnya tidak mencapai 1 karena tidak semua perempuan berambut panjang dan masih ada peluang orang yang berambut panjang adalah pria. |
||
Dari contoh di atas kita bisa merumuskan teorema Bayes secara umum. |
Dari contoh di atas kita bisa merumuskan teorema Bayes secara umum. |
||
| Baris 40: | Baris 44: | ||
== Pranala luar == |
== Pranala luar == |
||
* [http://www.idomaths.com/id/peluang5.php Teorema Bayes di situs I Do Maths] |
* [http://www.idomaths.com/id/peluang5.php Teorema Bayes di situs I Do Maths] |
||
* [http://repository.usu.ac.id/handle/123456789/17756 Peranan Teorema Bayes dalam mengambil keputusan] Repositori Universitas Sumatera Utara |
* [http://repository.usu.ac.id/handle/123456789/17756 Peranan Teorema Bayes dalam mengambil keputusan] {{Webarchive|url=https://web.archive.org/web/20100613014906/http://repository.usu.ac.id/handle/123456789/17756 |date=2010-06-13 }} Repositori Universitas Sumatera Utara |
||
* {{en}} [http://jeff560.tripod.com/b.html Earliest Known Uses of Some of the Words of Mathematics (B)]. Berisi asal istilah "Bayesian", "Bayes' Theorem", "Bayes Estimate/Risk/Solution", "Empirical Bayes", dan "Bayes Factor". |
* {{en}} [http://jeff560.tripod.com/b.html Earliest Known Uses of Some of the Words of Mathematics (B)]. Berisi asal istilah "Bayesian", "Bayes' Theorem", "Bayes Estimate/Risk/Solution", "Empirical Bayes", dan "Bayes Factor". |
||
* {{en}}[http://www.scholarpedia.org/article/Bayesian_statistics Statistika Bayes] ringkasan dari Scholarpedia. |
* {{en}}[http://www.scholarpedia.org/article/Bayesian_statistics Statistika Bayes] ringkasan dari Scholarpedia. |
||
Revisi terkini sejak 9 April 2023 06.45
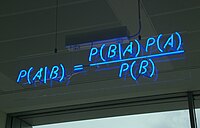
Dalam teori probabilitas dan statistika, teorema Bayes adalah sebuah teorema dengan dua penafsiran berbeda. Dalam penafsiran Bayes, teorema ini menyatakan seberapa jauh derajat kepercayaan subjektif seseorang harus berubah secara rasional ketika ada petunjuk atau informasi baru. Sebagai contoh di malam hari sebelum tidur, kita percaya secara subjektif bahwa besok akan cerah dan peluang hujan hanya 10%. Besok paginya kita bangun tidur dan mendengar berita ramalan cuaca bahwa sedang terjadi hujan lebat di berbagai kota maka kepercayaan subjektif kita berubah dan menaksir bahwa peluang hari ini akan hujan adalah 50%. Dalam penafsiran frekuentis teorema ini menjelaskan representasi invers probabilitas dua kejadian. Teorema ini merupakan dasar dari statistika Bayes dan memiliki penerapan dalam sains, rekayasa, ilmu ekonomi (terutama ilmu ekonomi mikro), teori permainan, kedokteran dan hukum. Penerapan teorema Bayes untuk memperbarui kepercayaan dinamakan inferens Bayes.
Pengenalan
[sunting | sunting sumber]Contoh singkat dari teorema bayes:
Misalkan kawan Anda bercerita dia bercakap-cakap akrab dengan seseorang lain di atas kereta api. Tanpa informasi tambahan, peluang dia bercakap-cakap dengan perempuan adalah 50%. Sekarang misalkan kawan Anda menyebut bahwa orang lain di atas kereta api itu berambut panjang. Dari keterangan baru ini tampaknya lebih boleh jadi kawan Anda bercakap-cakap dengan perempuan, karena orang berambut panjang biasanya wanita. Teorema Bayes dapat digunakan untuk menghitung besarnya peluang bahwa kawan Anda berbicara dengan seorang wanita, bila diketahui berapa peluang seorang wanita berambut panjang.
Misalkan:
- W adalah kejadian percakapan dilakukan dengan seorang wanita.
- L adalah kejadian percakapan dilakukan dengan seorang berambut panjang
- M adalah kejadian percakapan dilakukan dengan seorang pria
Kita dapat berasumsi bahwa wanita adalah setengah dari populasi. Artinya peluang kawan Anda berbicara dengan wanita,
Misalkan juga diketahui 75 persen wanita berambut panjang. Ini berarti bila kita mengetahui bahwa seseorang adalah wanita, peluangnya berambut panjang adalah 0,75. Kita melambangkannya sebagai:
Sebagai keterangan tambahan kita juga mengetahui bahwa peluang seorang pria berambut panjang adalah 0,3. Dengan kata lain:
Di sini kita mengasumsikan bahwa seseorang itu adalah pria atau wanita, atau P(M) = 1 - P(W) = 0,5. Dengan kata lain M adalah kejadian komplemen dari W.
Tujuan kita adalah menghitung peluang seseorang itu adalah wanita bila diketahui dia berambut panjang, atau dalam notasi yang kita gunakan, P(W|L). Menggunakan teorema Bayes, kita mendapatkan:
Di sini kita menggunakan aturan peluang total. Dengan memasukkan nilai-nilai peluang yang diketahui ke dalam rumus di atas, kita mendapatkan peluang seseorang itu wanita bila diketahui dia berambut panjang adalah 0,714. Angka ini sesuai dengan intuisi awal kita, bahwa peluang kawan kita itu bercakap-cakap dengan wanita meningkat. Walaupun demikian, peluangnya tidak mencapai 1 karena tidak semua perempuan berambut panjang dan masih ada peluang orang yang berambut panjang adalah pria.
Dari contoh di atas kita bisa merumuskan teorema Bayes secara umum.
Pernyataan
[sunting | sunting sumber]Bagian ini memerlukan pengembangan. Anda dapat membantu dengan mengembangkannya. |
Secara umum, teorema Bayes dinyatakan sebagai:
Dalam notasi ini P(A|B) berarti peluang kejadian A bila B terjadi dan P(B|A) peluang kejadian B bila A terjadi.
Pranala luar
[sunting | sunting sumber]- Teorema Bayes di situs I Do Maths
- Peranan Teorema Bayes dalam mengambil keputusan Diarsipkan 2010-06-13 di Wayback Machine. Repositori Universitas Sumatera Utara
- (Inggris) Earliest Known Uses of Some of the Words of Mathematics (B). Berisi asal istilah "Bayesian", "Bayes' Theorem", "Bayes Estimate/Risk/Solution", "Empirical Bayes", dan "Bayes Factor".
- (Inggris)Statistika Bayes ringkasan dari Scholarpedia.
- (Inggris)(Inggris) Weisstein, Eric W. "Bayes' Theorem". MathWorld.
- (Inggris)Bayes' theorem di PlanetMath.
- (Inggris)Tutorial tentang probabilitas dan teorema Bayes dirancang untuk mahasiswa psikologi Universitas Oxford
- (Inggris)Penjelasan grafis teorema Bayes.
- (Inggris) Aturan Bayes: tutorial oleh JV Stone.






