Gelombang sinus: Perbedaan antara revisi
Rescuing 1 sources and tagging 0 as dead.) #IABot (v2.0.8 |
Rescuing 2 sources and tagging 0 as dead.) #IABot (v2.0.9.5 |
||
| (5 revisi perantara oleh 4 pengguna tidak ditampilkan) | |||
| Baris 1: | Baris 1: | ||
| ⚫ | |||
{{short description|Kurva matematika yang menggambarkan osilasi berulang yang mulus; gelombang terus menerus}} |
{{short description|Kurva matematika yang menggambarkan osilasi berulang yang mulus; gelombang terus menerus}} |
||
{{refimprove}} |
|||
:''Untuk kegunaan lain, lihat [[Sinus (disambiguasi)]].'' |
:''Untuk kegunaan lain, lihat [[Sinus (disambiguasi)]].'' |
||
{{redirect|Sinusoid|pembuluh darah|Sinusoid (pembuluh darah)}} |
{{redirect|Sinusoid|pembuluh darah|Sinusoid (pembuluh darah)}} |
||
| ⚫ | |||
[[Berkas:Sine and Cosine.svg|thumb|400px|right|Grafik dari fungsi sinus (merah solid) dan [[Fungsi trigonometrik#Kosinus|kosinus]] (titik-titik biru) adalah sinusoid dengan fase yang berbeda]] |
[[Berkas:Sine and Cosine.svg|thumb|400px|right|Grafik dari fungsi sinus (merah solid) dan [[Fungsi trigonometrik#Kosinus|kosinus]] (titik-titik biru) adalah sinusoid dengan fase yang berbeda]] |
||
| Baris 36: | Baris 37: | ||
Persamaan ini menggambarkan gelombang sinus dalam satu dimensi, yaitu persamaan di atas menggambarkan amplitudo gelombang pada posisi ''x'' ketika waktu ''t'' dalam satu garis saja. |
Persamaan ini menggambarkan gelombang sinus dalam satu dimensi, yaitu persamaan di atas menggambarkan amplitudo gelombang pada posisi ''x'' ketika waktu ''t'' dalam satu garis saja. |
||
Contohnya gelombang pada seutas tali yang digoyang-goyangkan<ref>{{Cite web |url=http://www.regentsprep.org/Regents/math/algtrig/ATT7/sinusoidal.htm |title=Salinan arsip |access-date=2011-07-29 |archive-date=2011-07-19 |archive-url=https://web.archive.org/web/20110719092551/http://www.regentsprep.org/Regents/math/algtrig/ATT7/sinusoidal.htm |dead-url=yes }}</ref> |
Contohnya gelombang pada seutas tali yang digoyang-goyangkan.<ref>{{Cite web |url=http://www.regentsprep.org/Regents/math/algtrig/ATT7/sinusoidal.htm |title=Salinan arsip |access-date=2011-07-29 |archive-date=2011-07-19 |archive-url=https://web.archive.org/web/20110719092551/http://www.regentsprep.org/Regents/math/algtrig/ATT7/sinusoidal.htm |dead-url=yes }}</ref> |
||
Untuk gelombang yang lebih rumit, seperti gelombang air yang terbentuk dari batu yang dilempar kedalam kolam, maka diperlukan rumus yang lebih rumit pula<ref>http://hyperphysics.phy-astr.gsu.edu/hbase/sound/wavplt.html</ref> |
Untuk gelombang yang lebih rumit, seperti gelombang air yang terbentuk dari batu yang dilempar kedalam kolam, maka diperlukan rumus yang lebih rumit pula.<ref>{{Cite web |url=http://hyperphysics.phy-astr.gsu.edu/hbase/sound/wavplt.html |title=Salinan arsip |access-date=2011-07-29 |archive-date=2023-06-01 |archive-url=https://web.archive.org/web/20230601190627/http://hyperphysics.phy-astr.gsu.edu/hbase/Sound/wavplt.html |dead-url=no }}</ref> |
||
== Contoh kejadian == |
== Contoh kejadian == |
||
| Baris 45: | Baris 46: | ||
Gelombang ini sering muncul sehari-hari, misalnya [[gelombang laut]], gelombang [[suara]], dan gelombang [[cahaya]]. |
Gelombang ini sering muncul sehari-hari, misalnya [[gelombang laut]], gelombang [[suara]], dan gelombang [[cahaya]]. |
||
Gelombang [[kosinus]] merupakan gelombang "sinusoid" karena <math>\cos(x) = \sin(x + \pi/2),</math> sehingga gelombang kosinus sama seperti gelombang sinus dengan pergeseran fase sebesar n/2. Oleh karena gelombang ini fasenya lebih maju, sering pula dikatakan fungsi kosinus ''mendahului'' gelombang sinus, atau gelombang sinus ''terlambat'' dari kosinus<ref>{{Cite web |url=http://www.examstutor.com/physics/resources/studyroom/waves_and_oscillations/oscillations_and_harmonic_oscillations/ |title=Salinan arsip |access-date=2011-07-29 |archive-date=2011-10-02 |archive-url=https://web.archive.org/web/20111002130243/http://www.examstutor.com/physics/resources/studyroom/waves_and_oscillations/oscillations_and_harmonic_oscillations/ |dead-url=yes }}</ref> |
Gelombang [[kosinus]] merupakan gelombang "sinusoid" karena <math>\cos(x) = \sin(x + \pi/2),</math> sehingga gelombang kosinus sama seperti gelombang sinus dengan pergeseran fase sebesar n/2. Oleh karena gelombang ini fasenya lebih maju, sering pula dikatakan fungsi kosinus ''mendahului'' gelombang sinus, atau gelombang sinus ''terlambat'' dari kosinus.<ref>{{Cite web |url=http://www.examstutor.com/physics/resources/studyroom/waves_and_oscillations/oscillations_and_harmonic_oscillations/ |title=Salinan arsip |access-date=2011-07-29 |archive-date=2011-10-02 |archive-url=https://web.archive.org/web/20111002130243/http://www.examstutor.com/physics/resources/studyroom/waves_and_oscillations/oscillations_and_harmonic_oscillations/ |dead-url=yes }}</ref> |
||
[[Telinga]] manusia dapat menangkap gelombang sinus dari udara sebagai suara yang jernih karena hanya memiliki [[frekuensi]] tunggal tanpa [[harmonik]]; beberapa suara yang mendekati gelombang sinus sempurna adalah [[siulan]], gelas kristal yang dibunyikan dengan menggesekkan ujung jari pada bibir gelas, dan suara yang dihasilkan [[garpu tala]]<ref>http://www.triggertone.com/term/Sine_Wave</ref> |
[[Telinga]] manusia dapat menangkap gelombang sinus dari udara sebagai suara yang jernih karena hanya memiliki [[frekuensi]] tunggal tanpa [[harmonik]]; beberapa suara yang mendekati gelombang sinus sempurna adalah [[siulan]], gelas kristal yang dibunyikan dengan menggesekkan ujung jari pada bibir gelas, dan suara yang dihasilkan [[garpu tala]].<ref>{{Cite web |url=http://www.triggertone.com/term/Sine_Wave |title=Salinan arsip |access-date=2016-01-08 |archive-date=2016-03-19 |archive-url=https://web.archive.org/web/20160319162723/http://www.triggertone.com/term/Sine_Wave |dead-url=yes }}</ref> |
||
Gelombang suara yang terdiri dari beberapa sinyal sinus akan tertangkap telinga sebagai bunyi "berisik" atau memiliki [[harmonik]] tertentu; dikatakan suara tersebut memiliki "warna" ([[timbre]]). |
Gelombang suara yang terdiri dari beberapa sinyal sinus akan tertangkap telinga sebagai bunyi "berisik" atau memiliki [[harmonik]] tertentu; dikatakan suara tersebut memiliki "warna" ([[timbre]]). |
||
| Baris 61: | Baris 62: | ||
[[Kategori:Trigonometri]] |
[[Kategori:Trigonometri]] |
||
[[Kategori: |
[[Kategori:Mekanika gelombang]] |
||
[[Kategori:Gelombang]] |
[[Kategori:Gelombang|Sinus]] |
||
Revisi terkini sejak 30 Juli 2023 01.18
Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. (Oktober 2020) |
- Untuk kegunaan lain, lihat Sinus (disambiguasi).

Gelombang sinus atau sinusoidal adalah fungsi matematika yang berbentuk osilasi halus berulang. Fungsi ini sering muncul dalam ilmu matematika, fisika, pengolahan sinyal, dan teknik listrik, dan berbagai bidang lain. Bentuk paling sederhana dari fungsi ini terhadap waktu )t) adalah:
di mana:
- A, amplitudo, adalah puncak simpangan fungsi dari posisi tengahnya,
- ω, frekuensi sudut, menunjukkan berapa banyak gerak bolak-balik yang terjadi dalam satu satuan waktu, dalam radian per detik,
- φ, fase, menunjukkan di mana posisi awal gerakan ketika t=0,
- Jika fase tidak bernilai nol, seluruh gelombang akan tampak bergeser menurut sumbu X (sumbu waktu) sebesar φ/ω detik. Nilai negatif pada fase menunjukkan jeda, sedang nilai positif menunjukkan gelombang "berangkat lebih awal".
Gelombang sinus sangat penting dalam bidang fisika karena gelombang ini mempertahankan bentuknya ketika ditambahkan kepada gelombang sinus berfrekuensi sama yang lain walaupun fasenya berbeda. Gelombang ini merupakan satu-satunya fungsi periodik yang memiliki sifat ini. Sifat ini menjadikan gelombang ini bagian penting dalam Analisis Fourier.
Bentuk Umum
[sunting | sunting sumber]Secara umum, fungsi ini dapat memiliki:
- dimensi ruang, x (posisi), dengan frekuensi k (juga disebut nomor gelombang)
- titik tengah amplitudo tidak bernilai nol, D (disebut bias DC)
dengan rumus:
Nomor gelombang bergantung pada frekuensi sudut dengan rumus:
di mana λ adalah panjang gelombang, f adalah frekuensi, dan c adalah kecepatan fase
Persamaan ini menggambarkan gelombang sinus dalam satu dimensi, yaitu persamaan di atas menggambarkan amplitudo gelombang pada posisi x ketika waktu t dalam satu garis saja. Contohnya gelombang pada seutas tali yang digoyang-goyangkan.[1]
Untuk gelombang yang lebih rumit, seperti gelombang air yang terbentuk dari batu yang dilempar kedalam kolam, maka diperlukan rumus yang lebih rumit pula.[2]
Contoh kejadian
[sunting | sunting sumber]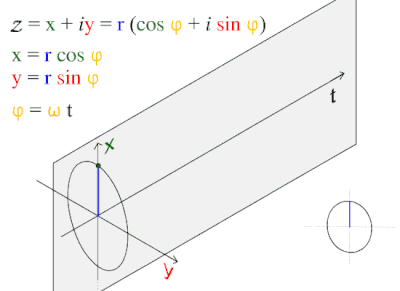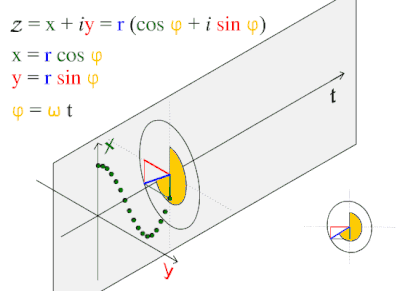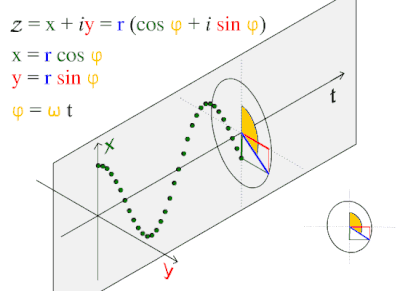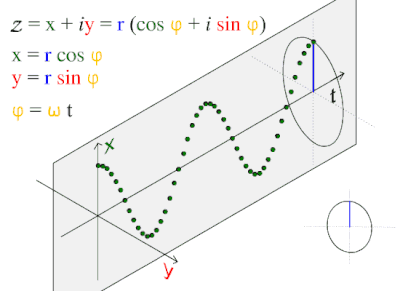
Gelombang ini sering muncul sehari-hari, misalnya gelombang laut, gelombang suara, dan gelombang cahaya.
Gelombang kosinus merupakan gelombang "sinusoid" karena sehingga gelombang kosinus sama seperti gelombang sinus dengan pergeseran fase sebesar n/2. Oleh karena gelombang ini fasenya lebih maju, sering pula dikatakan fungsi kosinus mendahului gelombang sinus, atau gelombang sinus terlambat dari kosinus.[3]
Telinga manusia dapat menangkap gelombang sinus dari udara sebagai suara yang jernih karena hanya memiliki frekuensi tunggal tanpa harmonik; beberapa suara yang mendekati gelombang sinus sempurna adalah siulan, gelas kristal yang dibunyikan dengan menggesekkan ujung jari pada bibir gelas, dan suara yang dihasilkan garpu tala.[4]
Gelombang suara yang terdiri dari beberapa sinyal sinus akan tertangkap telinga sebagai bunyi "berisik" atau memiliki harmonik tertentu; dikatakan suara tersebut memiliki "warna" (timbre).
Seri Fourier
[sunting | sunting sumber]
Pada tahun 1822, Joseph Fourier, seorang ahli matematika Prancis, menemukan bahwa gelombang sinusoid dapat digunakan untuk membentuk (paling tidak mendekati) semua gelombang periodik, termasuk gelombang persegi. Fourier menggunakan penemuan ini sebagai alat untuk menganalisis gelombang dan aliran panas. Analisis ini sering digunakan dalam pengolahan sinyal dan analisis statistik seri waktu.
Referensi
[sunting | sunting sumber]- ^ "Salinan arsip". Diarsipkan dari versi asli tanggal 2011-07-19. Diakses tanggal 2011-07-29.
- ^ "Salinan arsip". Diarsipkan dari versi asli tanggal 2023-06-01. Diakses tanggal 2011-07-29.
- ^ "Salinan arsip". Diarsipkan dari versi asli tanggal 2011-10-02. Diakses tanggal 2011-07-29.
- ^ "Salinan arsip". Diarsipkan dari versi asli tanggal 2016-03-19. Diakses tanggal 2016-01-08.




