Fungsi trigonometri: Perbedaan antara revisi
Tag: Suntingan perangkat seluler Suntingan peramban seluler Suntingan seluler lanjutan |
Fitur saranan suntingan: 3 pranala ditambahkan. Tag: VisualEditor Suntingan perangkat seluler Suntingan peramban seluler Tugas pengguna baru Disarankan: tambahkan pranala |
||
| (41 revisi perantara oleh 9 pengguna tidak ditampilkan) | |||
| Baris 1: | Baris 1: | ||
{{Trigonometri}} |
|||
{{anchor|cos|tan|cot|sec|csc}} |
|||
[[Berkas:Academ Base of trigonometry.svg|jmpl|300x300px|Dasar trigonometri mengatakan bahwa jika dua [[segitiga siku-siku]] mempunyai [[sudut lancip]] yang sama, maka segitiga dikatakan [[Kesebangunan|sebangun]] sehingga panjang sisinya [[Kesebandingan (matematika)|sebanding]].]] |
|||
{{Dalam perbaikan}} |
|||
Dalam [[matematika]], '''fungsi trigonometri''' merupakan [[fungsi real]] yang mengaitkan sudut dari [[Segitiga siku|segitiga bersiku]] dengan perbandingan antara dua sisi segitiga. Fungsi ini memiliki penerapan yang sangat luas dalam bidang sains terkait dengan [[geometri]] (misalnya navigasi, [[geodesi]], [[mekanika benda langit]], [[mekanika zat padat]], dan cabang lainnya). Fungsi ini merupakan contoh [[fungsi periodik]] paling sederhana, dan juga memiliki penerapan yang sangat luas dalam mempelajari fenomena periodik melalui [[analisis Fourier]]. |
|||
[[Berkas:Academ Base of trigonometry.svg|thumb|300px|upright=2|Basis of trigonometry: if two [[right triangle]]s have equal [[Types of angles|acute angles]], they are [[Similarity (geometry)|similar]], so their side lengths [[Proportionality (mathematics)|are proportional]]. Proportionality [[constant (mathematics)|constant]]s are written within the image: {{math|sin ''θ''}}, {{math|cos ''θ''}}, {{math|tan ''θ''}}, where {{mvar|θ}} is the common measure of five acute angles.]] |
|||
'''Fungsi trigonometrik''' adalah fungsi dari sebuah sudut yang digunakan untuk menghubungkan antara sudut-sudut dalam suatu segitiga dengan sisi-sisi segitiga tersebut. |
|||
Fungsi trigonometri seperti '''[[Sinus (trigonometri)|sinus]]''', '''[[kosinus]]''', dan '''tangen''' merupakan fungsi yang paling sering dipakai dalam [[matematika modern]]; sedangkan fungsi [[Perkalian invers|inversnya]] seperti '''kosekan''', '''sekan''', dan '''kotangen''' jarang dipakai. Masing-masing keenam fungsi tersebut mempunyai [[fungsi invers]] yang sama dan sejalan di antara [[fungsi hiperbolik]]. |
|||
[[Berkas:Rtriangle.svg|200px|ka]] |
|||
Definisi fungsi trigonometri terlama, yang berkaitan dengan segitiga bersudutkan siku-siku, hanya mendefinisikannya untuk [[sudut lancip]]. Secara geometris, fungsi sinus dan kosinus seringkali dapat diperluas menjadi fungsi yang mempunyai [[Domain fungsi|domain]] yang mengandung seluruh [[garis bilangan real]], maka domain fungsi lainnya adalah garis bilangan real dengan setiap titik terpencilnya hilang. Definisi modern yang mengekspresikan fungsi trigonometri sebagai [[deret takhingga]] atau sebagai penyelesai dari [[persamaan diferensial]], memungkinkan perluasan domain dari fungsi sinus dan kosinus menjadi domain yang mengandung seluruh [[bidang kompleks]], dan domain dari fungsi trigonometri lain menjadi domain mengandung bidang kompleks dengan setiap titik terpencilnya hilang. |
|||
Fungsi trigonometrik diringkas di tabel di bawah ini. Sudut <math>\theta</math> adalah sudut yang diapit oleh sisi miring dan sisi samping—sudut A pada gambar di samping, a adalah sisi depan, b adalah sisi samping, dan c adalah sisi miring: |
|||
<!--{| class=wikitable style="margin-left:1em" |
|||
! style="text-align:left" | '''Fungsi''' |
|||
! style="text-align:left" | '''Singkatan''' |
|||
! style="text-align:left" | '''Deskripsi''' |
|||
! style="text-align:left" | '''Identitas (memggunakan [[radian]])''' |
|||
|- style="background-color:#FFFFFF" |
|||
| '''[[Sinus]]''' |
|||
| sin |
|||
| <math>\frac {\textrm{a}} {\textrm{c}} </math> |
|||
| <math>\sin \theta \equiv \cos \left(\frac{\pi}{2} - \theta \right) \equiv \frac{1}{\csc \theta}\,</math> |
|||
|- style="background-color:#FFFFFF" |
|||
| '''[[Kosinus]]''' |
|||
| cos |
|||
| <math>\frac {\textrm{b}} {\textrm{c}} </math> |
|||
| <math>\cos \theta \equiv \sin \left(\frac{\pi}{2} - \theta \right) \equiv \frac{1}{\sec \theta}\,</math> |
|||
|- style="background-color:#FFFFFF" |
|||
| '''[[Tangen]]''' |
|||
| tan (atau tg) |
|||
|align=center| <math>\frac {\textrm{a}} {\textrm{b}} </math> |
|||
| <math>\tan \theta \equiv \frac{\sin \theta}{\cos \theta} \equiv \cot \left(\frac{\pi}{2} - \theta \right) \equiv \frac{1}{\cot \theta} \,</math> |
|||
|- style="background-color:#FFFFFF" |
|||
| '''[[Kotangen]]''' |
|||
| cot (atau ctg atau ctn) |
|||
|align=center| <math>\frac {\textrm{b}} {\textrm{a}} </math> |
|||
| <math>\cot \theta \equiv \frac{\cos \theta}{\sin \theta} \equiv \tan \left(\frac{\pi}{2} - \theta \right) \equiv \frac{1}{\tan \theta} \,</math> |
|||
|- style="background-color:#FFFFFF" |
|||
| '''[[Sekan]]''' |
|||
| sec |
|||
| <math>\frac {\textrm{c}} {\textrm{b}} </math> |
|||
| <math>\sec \theta \equiv \csc \left(\frac{\pi}{2} - \theta \right) \equiv\frac{1}{\cos \theta} \,</math> |
|||
|- style="background-color:#FFFFFF" |
|||
| '''[[Kosekan]]''' |
|||
| csc (atau cosec) |
|||
| <math>\frac {\textrm{c}} {\textrm{a}} </math> |
|||
| <math>\csc \theta \equiv \sec \left(\frac{\pi}{2} - \theta \right) \equiv\frac{1}{\sin \theta} \,</math> |
|||
|}--> |
|||
== Notasi == |
|||
== Definisi segitiga siku-siku == |
|||
Fungsi trigonometri biasanya menyingkatkan namanya menggunakan tiga huruf, contohnya: [[Sinus (trigonometri)|sinus]] disingkat "sin", [[kosinus]] "cos", [[tangen]] disingkat "tan", [[sekan]] disingkat "sec", [[kosekan]] disingkat "csc",{{Efn|Kosekan terkadang juga disingkat dengan lima huruf, yaitu "cosec".}} dan [[kotangen]] disingkat "cot". Terlebih lagi, fungsi trigonometri juga menggunakan [[Fungsi (matematika)#Notasi fungsional|notasi fungsional]], misalnya {{math|sin(''x'')}}. Tanda kurung wajib digunakan karena dapat menimbulkan kebingungan. Sebagai contohnya seperti fungsi <math>\sin x+y</math> dapat dipandang sebagai <math>\sin (x)+y</math> atau juga dapat dipandang sebagai <math>\sin (x+y)</math>. |
|||
[[Berkas:Trigonometry triangle.svg|right|200px|thumb|Segitiga siku-siku selalu mencakup pada 90° ({{sfrac|{{pi}}|2}} radian) sudut, hal ini berlabel ''C''. Sudut ''A'' dan ''B'' dapat bervariasi. Fungsi trigonometri menentukan hubungan antara panjang sisi dan sudut dalam segitiga siku-siku.]] |
|||
[[Berkas:TrigFunctionDiagram.svg|thumb|Plot dari enam fungsi trigonometri, lingkaran satuan, dan garis untuk sudut {{math|1=θ = 0.7}} radian. Poinnya diberikan pada label {{color|#A00|1}}, {{color|#00A|Sec(θ)}}, {{color|#0A0|Csc(θ)}} mewakili panjang ruas garis dari titik asal ke titik tersebut. {{color|#A00|Sin(θ)}}, {{color|#00A|Tan(θ)}}, dan {{color|#0A0|1}} adalah ketinggian ke garis mulai dari {{mvar|x}}-sumbu, sementara {{color|#A00|Cos(θ)}}, {{color|#00A|1}}, dan {{color|#0A0|Cot(θ)}} adalah panjang di sepanjang {{mvar|x}}-sumbu dimulai dari asalnya.]] |
|||
Tidak seperti notasi fungsi lainnya, [[bilangan bulat positif]] yang muncul sebagai superskrip setelah simbol fungsi, bukan dinyatakan sebagai perpangkatan terhadap [[komposisi fungsi]], melainkan dinyatakan sebagai perkalian teriterasi. Sebagai contoh, <math>\sin^2 x</math> dan <math>\sin^2 (x)</math> berarti <math>\sin(x) \sin(x)</math>, bukan <math>\sin(\sin x)</math>. |
|||
''Pada bagian tersebut, huruf yang besar dengan bentuk sama menunjukkan titik puncak segitiga dan ukuran sudut yang sesuai; huruf kecil yang sama menunjukkan tepi segitiga dan panjangnya.'' |
|||
Eksponen <math>{-1}</math> biasanya dipakai untuk menyatakan [[fungsi invers]], bukan [[invers perkalian]]. Sebagai contoh, <math>\sin^{-1}x</math> dan <math>\sin^{-1}(x)</math> menyatakan [[fungsi invers trigonometri]], dan notasi tersebut dapat ditulis pula sebagai <math>\arcsin x</math>. Persamaan <math>\theta = \sin^{-1}x</math> menyiratkan <math>\sin \theta = x</math>, bukan <math>\theta \cdot \sin x = 1</math>. Pada kasus tersebut, superskrip ''dapat'' dipandang untuk menyatakan [[fungsi teriterasi|fungsi yang berulang]], tetapi superskrip yang bernilai negatif selain <math>{-1}</math> jarang dipakai. |
|||
Diberikan [[sudut akut]] pada nilai {{mvar|A}} = {{mvar|θ}} dari sebuah [[segitiga siku-siku]] dan [[sisi miring]] pada nilai {{mvar|h}} adalah sisi yang menghubungkan dua sudut lancip. Sisi {{mvar|b}} berdekatan dengan {{mvar|θ}} adalah sisi segitiga yang menghubungkan nilai {{mvar|θ}} ke sudut kanan. Sisi ketiga {{mvar|a}} dikatakan ''nilai berlawanan'' dengan nilai {{mvar|θ}}. |
|||
== Definisi segitiga bersiku == |
|||
Jika sudut pada nilai {{mvar|θ}} akan diberikan nilai maka semua sisi segitiga siku-siku ditentukan dengan baik hingga faktor skala. Hal tersebut berarti bahwa perbandingan dua panjang sisi mana pun hanya bergantung pada {{mvar|θ}}. Jadi, enam rasio tersebut mendefinisikan enam fungsi pada nilai {{mvar|θ}}, merupakan salah satu fungsi trigonometri. Lebih tepatnya, enam fungsi trigonometri adalah:<ref>{{harvtxt|Protter|Morrey|1970|pp=APP-2, APP-3}}</ref> |
|||
[[Berkas:TrigonometryTriangle.svg|jmpl|Dalam segitiga siku-siku {{Math|''BAC''}}, ketiga fungsi trigonometri dari sudut {{Math|''A''}} dinyatakan sebagai: {{math|1=sin ''A'' = {{sfrac|''a''|''c''}}}}, {{math|1=cos ''A'' = {{sfrac|''b''|''c''}}}}, dan {{math|1=tan ''A'' = {{sfrac|''a''|''b''}}}}.]] |
|||
[[Berkas:TrigFunctionDiagram.svg|jmpl|Plot dari enam fungsi trigonometri, lingkaran satuan, dan sebuah garis yang membentuk sudut dengan sumbu-{{mvar|x}} sebesar {{math|1=''θ'' = 0,7 rad}}.Pada plot tersebut, terdapat titik-titik yang dilabeli {{color|#D00|1}}, {{color|#02D|Sec(''θ'')}}, {{color|#0D1|Csc(''θ'')}} mewakili panjang ruas garis yang ditarik dari titik asal ke titik tersebut. Titik-titik seperti {{color|#D00|Sin(''θ'')}}, {{color|#02D|Tan(''θ'')}}, dan {{color|#0D1|1}} merupakan panjang garis yang ditarik dari sumbu-{{mvar|x}}, sedangkan titik seperti {{color|#D00|Cos(''θ'')}}, {{color|#02D|1}}, dan {{color|#0D1|Cot(''θ'')}} merupakan panjang di sekitar sumbu-{{mvar|x}} yang ditarik dari titik asal.]] |
|||
;sinus: <math>\sin \theta= \frac a h = \frac \mathrm{opposite}\mathrm{hypotenuse}</math> |
|||
Jika sudut lancip dinyatakan sebagai {{mvar|θ}}, maka setiap sudut siku-siku yang mempunyai sudut {{mvar|θ}} dikatakan [[Kesebangunan (geometri)|sebangun]] terhadap satu sama lain; dalam artian, perbandingan dari setiap dua panjang sisinya hanya bergantung pada {{mvar|θ}}. Jadi, keenam perbandingan tersebut mendefinisikan enam fungsi trigonometri dari {{mvar|θ}}. Definisi berikut mengatakan bahwa [[hipotenusa]] (sisi miring) merupakan panjang dari sisi yang berhadapan dengan sudut siku-siku, sisi depan merupakan panjang sisi yang berhadap dari sudut {{mvar|θ}}, dan sisi samping merupakan panjang sisi yang berhadapan dengan sudut {{mvar|θ}} dan sudut siku-siku.<ref>{{harvtxt|Protter|Morrey|1970|pp=APP-2, APP-3}}</ref><ref>{{Cite web|title=Sine, Cosine, Tangent|url=https://www.mathsisfun.com/sine-cosine-tangent.html|website=www.mathsisfun.com|access-date=29 August 2020|archive-date=2023-06-30|archive-url=https://web.archive.org/web/20230630135422/https://www.mathsisfun.com/sine-cosine-tangent.html|dead-url=no}}</ref> |
|||
;kosinus: <math>\cos \theta= \frac b h = \frac \mathrm{adjacent}\mathrm{hypotenuse}</math> |
|||
{| |
|||
;tangen: <math>\tan \theta= \frac a b = \frac \mathrm{opposite}\mathrm{adjacent}</math> |
|||
| style="padding-left: 2em; padding-right: 2em; " | |
|||
;koseken: <math>\csc \theta= \frac h a = \frac \mathrm{hypotenuse}\mathrm{opposite}</math> |
|||
; sinus |
|||
;seken: <math>\sec \theta= \frac h b = \frac \mathrm{hypotenuse}\mathrm{adjacent}</math> |
|||
: <math>\sin \theta = \frac \mathrm{depan}\mathrm{miring}</math> |
|||
| style="padding-left: 2em; padding-right: 2em; " | |
|||
; kosekan |
|||
Dalam segitiga siku-siku, hasil penjumlahan dari dua sudut lancip adalah sudut siku-siku, yaitu 90° atau <math display="inline">\frac \pi 2</math> pada [[radian]]. |
|||
: <math>\csc \theta = \frac \mathrm{miring}\mathrm{depan}</math> |
|||
{| class="wikitable sortable" |
|||
|+ Ringkasan hubungan antara fungsi trigonometrik<ref>{{harvtxt|Protter|Morrey|1970|p=APP-7}}</ref> |
|||
|- |
|- |
||
| style="padding-left: 2em; padding-right: 2em; " | |
|||
! rowspan=2 | Fungsi |
|||
; kosinus |
|||
! rowspan=2 | Singkatan |
|||
: <math>\cos \theta = \frac \mathrm{samping}\mathrm{miring}</math> |
|||
! rowspan=2 | Deskripsi |
|||
| style="padding-left: 2em; padding-right: 2em; " | |
|||
! colspan=2 | [[Daftar identitas trigonometrik|Hubungan antara trigonometrik]] |
|||
; sekan |
|||
: <math>\sec \theta = \frac \mathrm{miring}\mathrm{samping}</math> |
|||
|- |
|||
| style="padding-left: 2em; padding-right: 2em; " | |
|||
; tangen |
|||
: <math>\tan \theta = \frac \mathrm{depan}\mathrm{samping}</math> |
|||
| style="padding-left: 2em; padding-right: 2em; " | |
|||
; kotangen |
|||
: <math>\cot \theta = \frac \mathrm{samping}\mathrm{depan}</math> |
|||
|} |
|||
Dalam segitiga siku-siku, jumlah dari dua sudut lancip sama dengan sudut siku-siku, yaitu {{math|90°}} atau {{math|{{sfrac|''π''|2}}}} [[radian]]. Karena itu, <math>\sin(\theta)</math> dan <math>\cos(90^\circ - \theta)</math> mewakili perbandingan yang sama sehingga menjadi sama. Identitas dan kaitan antara fungsi trigonometri lainnya yang sejalan diringkas dalam tabel berikut. |
|||
[[Berkas:Periodic sine.svg|jmpl|'''Gambar atas:''' Fungsi trigonometri {{math|sin ''θ''}} untuk sudut {{math|''θ''}}, {{math|{{pi}} − ''θ''}}, {{math|{{pi}} + ''θ''}}, dan {{math|2{{pi}} − ''θ''}} dalam empat kuadran.<br><br>'''Gambar bawah:''' Perbandingan grafik fungsi dengan sudut sinus. Sudut-sudut dari panel di atas diidentifikasi]] |
|||
{| class="wikitable sortable" |
|||
|+Ringkasan mengenai kaitan antara fungsi trigonometri<ref>{{harvtxt|Protter|Morrey|1970|p=APP-7}}</ref> |
|||
! rowspan="2" |Fungsi |
|||
! rowspan="2" |Penjelasan |
|||
! colspan="2" |[[Daftar identitas trigonometri|Kaitan]] |
|||
|- |
|- |
||
! |
!dalam bentuk [[radian]] |
||
! |
!dalam bentuk [[Derajat (satuan sudut)|derajat]] |
||
|- |
|- |
||
! |
!sinus |
||
| align="center" |{{math|{{sfrac|depan|miring}}}} |
|||
| sin |
|||
|<math>\sin \theta = \cos\left(\frac{\pi}{2} - \theta \right) = \frac{1}{\csc \theta}</math> |
|||
|align=center|{{sfrac|opposite|hypotenuse}} |
|||
| |
|<math>\sin x = \cos\left(90^\circ - x \right) = \frac{1}{\csc x}</math> |
||
| <math>\sin x = \cos\left(90^\circ - x \right) = \frac{1}{\csc x}</math> |
|||
|- |
|- |
||
! |
!kosinus |
||
| align="center" |{{math|{{sfrac|samping|miring}}}} |
|||
| cos |
|||
|<math>\cos \theta = \sin\left(\frac{\pi}{2} - \theta \right) = \frac{1}{\sec \theta}\,</math> |
|||
|align=center|{{sfrac|adjacent|hypotenuse}} |
|||
| |
|<math>\cos x = \sin\left(90^\circ - x \right) = \frac{1}{\sec x}\,</math> |
||
| <math>\cos x = \sin\left(90^\circ - x \right) = \frac{1}{\sec x}\,</math> |
|||
|- |
|- |
||
! |
!tangen |
||
| align="center" |{{math|{{sfrac|depan|samping}}}} |
|||
| tan (or tg) |
|||
|<math>\tan \theta = \frac{\sin \theta}{\cos \theta} = \cot\left(\frac{\pi}{2} - \theta \right) = \frac{1}{\cot \theta} </math> |
|||
|align=center|{{sfrac|opposite|adjacent}} |
|||
| |
|<math>\tan x = \frac{\sin x}{\cos x} = \cot\left(90^\circ - x \right) = \frac{1}{\cot x} </math> |
||
| <math>\tan x = \frac{\sin x}{\cos x} = \cot\left(90^\circ - x \right) = \frac{1}{\cot x} </math> |
|||
|- |
|- |
||
! |
!kotangen |
||
| align="center" |{{math|{{sfrac|samping|miring}}}} |
|||
| cot (or cotan or cotg or ctg or ctn) |
|||
|<math>\cot \theta = \frac{\cos \theta}{\sin \theta} = \tan\left(\frac{\pi}{2} - \theta \right) = \frac{1}{\tan \theta} </math> |
|||
|align=center|{{sfrac|adjacent|opposite}} |
|||
| |
|<math>\cot x = \frac{\cos x}{\sin x} = \tan\left(90^\circ - x \right) = \frac{1}{\tan x} </math> |
||
| <math>\cot x = \frac{\cos x}{\sin x} = \tan\left(90^\circ - x \right) = \frac{1}{\tan x} </math> |
|||
|- |
|- |
||
! |
!sekan |
||
| align="center" |{{math|{{sfrac|miring|samping}}}} |
|||
| sec |
|||
|<math>\sec \theta = \csc\left(\frac{\pi}{2} - \theta \right) = \frac{1}{\cos \theta} </math> |
|||
|align=center|{{sfrac|hypotenuse|adjacent}} |
|||
| |
|<math>\sec x = \csc\left(90^\circ - x \right) = \frac{1}{\cos x} </math> |
||
| <math>\sec x = \csc\left(90^\circ - x \right) = \frac{1}{\cos x} </math> |
|||
|- |
|- |
||
! |
!kosekan |
||
| align="center" |{{math|{{sfrac|miring|depan}}}} |
|||
| csc (or cosec) |
|||
|<math>\csc \theta = \sec\left(\frac{\pi}{2} - \theta \right) = \frac{1}{\sin \theta} </math> |
|||
|align=center|{{sfrac|hypotenuse|opposite}} |
|||
| |
|<math>\csc x = \sec\left(90^\circ - x \right) = \frac{1}{\sin x} </math> |
||
| <math>\csc x = \sec\left(90^\circ - x \right) = \frac{1}{\sin x} </math> |
|||
|} |
|} |
||
[[Berkas:Periodic sine.PNG|thumb|'''Daftar:''' Fungsi trigonometrik <!--{{math|sin θ}} for selected angles {{math|θ}}, {{math|{{pi}} − θ}}, {{math|{{pi}} + θ}}, and {{math|2{{pi}} − θ}} in the four quadrants.<br>'''Bottom:''' Graph of sine function versus angle. Angles from the top panel are identified.-->]] |
|||
== |
== Perbandingan radian dengan derajat == |
||
Dalam penerapan geometri, argumen fungsi trigonometri umumnya merupakan ukuran [[sudut]]. Setiap [[sudut]] biasanya diukur dan satuan konvensional berupa [[Derajat (satuan sudut)|derajat]]. Sebagai contoh, sudut siku-siku ditulis 90° dan putaran penuh ditulis 360°.{{Efn|Satuan konvensional ini khususnya dipakai dalam [[matematika elementer]].}} |
|||
{{Unreferenced|section|date=August 2020}} |
|||
Dalam aplikasi geometris, argumen fungsi trigonometri umumnya adalah ukuran pada [[sudut]]. Untuk tujuan setiap [[satuan sudut]] adalah sudut yang paling sering diukur |
|||
Namun dalam [[kalkulus]] dan [[analisis matematika]], fungsi trigonometri umumnya dipandang lebih abstrak sebagai fungsi [[Bilangan real|real]] ataupun [[Bilangan kompleks|kompleks]], bukan sudut. Bahkan fungsi sepeti '''sin''' dan '''cos''' dapat didefinisikan untuk semua bilangan kompleks dalam bentuk [[fungsi eksponensial]] melalui deret pangkat,<ref name=":0">{{Cite book|last=Rudin, Walter, 1921–2010|url=https://www.worldcat.org/oclc/1502474|title=Principles of mathematical analysis|location=New York|isbn=0-07-054235-X|edition=Third|oclc=1502474|access-date=2022-08-18|archive-date=2020-01-23|archive-url=https://web.archive.org/web/20200123033536/https://www.worldcat.org/title/principles-of-mathematical-analysis/oclc/1502474|dead-url=no}}</ref> atau dapat didefinisikan sebagai penyelesaian nilai awal khusus terhadap [[persamaan diferensial]] (lihat [[Pengguna:Dedhert.Jr/Uji halaman 15#Definisi trigonometri melalui persamaan diferensial|dibawah]]).<ref>{{Cite journal|last=Diamond|first=Harvey|date=2014|title=Defining Exponential and Trigonometric Functions Using Differential Equations|url=https://www.tandfonline.com/doi/full/10.4169/math.mag.87.1.37|journal=Mathematics Magazine|language=en|volume=87|issue=1|pages=37–42|doi=10.4169/math.mag.87.1.37|issn=0025-570X|s2cid=126217060}}</ref> Definisi tersebut tidak mengacu pada gagasan dalam geometri. Adapun empat fungsi lainnya seperti '''tan''', '''cot''', '''sec''', dan '''csc''' dapat didefinisikan sebagia hasil-bagi dan timbal balik dari '''sin''' dan '''cos''', kecuali ketika nol muncul di penyebut. Untuk argumen real, hal ini dapat dibuktikan bahwa definisi tersebut sesuai dengan definisi geometri elementer ''jika argumennya dipandang sebagai sudut yang dinyatakan dalam bentuk radian''.<ref name=":0" /> Lebih lanjut, definisi tersebut memberikan hasil dalam bentuk yang sederhana untuk [[turunan]] dan [[integral taktentu]] dari fungsi trigonometri.<ref name=":1">{{Cite book|last=Spivak|first=Michael|year=1967|title=Calculus|publisher=Addison-Wesley|pages=256–257|chapter=15|lccn=67-20770}}</ref> Jadi dalam cabang selain geometri elementer, radian dipandang sebagai satuan alami dalam matematika untuk menjelaskan ukuran setiap sudut. |
|||
Saat menggunakan fungsi trigonometri dalam [[kalkulus]], argumennya umumnya bukan sudut, melainkan [[bilangan real]]. Dalam hal ini, lebih cocok untuk mengungkapkan argumen trigonometri pada unit<!--: a radian is the angle that delimits an arc of length {{val|1}} on the unit circle. A complete [[turn (angle)|turn]] is thus an angle of {{math|2''{{pi}}''}} radians. |
|||
Ketika satuan yang dipakai adalah [[radian]], maka sudut dinyatakan sebagai panjang [[Busur (geometri)|busur]] dari [[lingkaran satuan]] yang berhadapan dengannya. Sebagai contoh, sudut yang berhadapan dengan busur dengan panjang 1 di lingkaran satuan adalah 1 rad (≈ 57,3°), dan [[Putaran (sudut)|putaran]] penuh (360°) sama dengan 2{{pi}} (≈ 6,28) rad. Untuk bilangan real {{Math|''x''}}, notasi {{Math|sin ''x''}}, {{Math|cos ''x''}}, dst. mengacu pada nilai dari fungsi trigonometri yang dihitung pada sudut ''{{Math|''x''}}'' rad. Jika satuan yang dimaksud adalah derajat, maka tanda derajat harus diperlihatkan secara eksplisit (sebagai contoh, {{Math|sin ''x''°}}, {{Math|cos ''x''°}}, dsb.). Dengan menggunakan notasi yang standar, argumen dari {{Math|''x''}} untuk fungsi trigonometri memenuhi kaitan dari rumus |
|||
A great advantage of radians is that many formulas are much simpler when using them, typically all formulas relative to [[derivative]]s and [[integral]]s. |
|||
: <math>x = \left(\frac{180x}{\pi}\right)^\circ,</math> |
|||
This is thus a general convention that, when the angular unit is not explicitly specified, ''the arguments of trigonometric functions are always expressed in radians.''--> |
|||
sehingga, sebagai contoh, {{Math|1=sin ''{{pi}}'' = sin 180°}} ketika {{math|1=''x'' = {{pi}}}}. Dalam cara ini, simbol derajat dapat dipandang sebagai sebuah konstanta matematika, sehingga {{math|1= 1° = {{sfrac|1={{pi}}|2=180}} ≈ 0,0175}}. |
|||
== Definisi lingkaran unit == |
|||
[[Berkas:Unit Circle Definitions of Six Trigonometric Functions.png|thumb|300x300px|Dalam ilustrasi ini, enam fungsi trigonometri dari sudut sembarang {{math|''θ''}} direpresentasikan sebagai [[koordinat kartesius]] dari titik-titik yang terkait dengan [[lingkaran unit]]. Koordinat dari {{math|A}}, {{math|B}} dan {{math|D}} adalah {{math|sin ''θ''}}, {{math|tan ''θ''}} dan {{math|csc ''θ''}}, masing-masing, sedangkan absis dari {{math|A}}, {{math|C}} dan {{math|E}} adalah {{math|cos ''θ''}}, {{math|cot ''θ''}} dan {{math|sec ''θ''}}, masing-masing.]] |
|||
[[Berkas:trigonometric function quadrant sign.svg|thumb|<!--Tanda fungsi trigonometri di setiap kuadran. Mnemonik tersebut "'''t''' '''s'''ins '''t'''eachers (are) '''c'''razy" lists the functions which are positive from quadrants I to IV.<ref name="Heng"/> This is a variation on the mnemonic "[[All Students Take Calculus]]".-->]] |
|||
== Definisi fungsi trigonometri melalui lingkaran satuan == |
|||
Enam fungsi trigonometri dapat didefinisikan sebagai [[Sistem koordinat kartesius|nilai koordinat kartesius]] titik pada [[bidang Euklides]] yang terkait dengan [[lingkaran satuan]] yang merupakan [[lingkaran]] pada jari-jari salah satu yang berpusat di titik asal {{math|O}} dari sistem koordinat tersebut. Sedangkan [[# definisi segitiga siku-siku|definisi segitiga siku-siku]] mengizinkan definisi fungsi trigonometri untuk sudut antara nilai {{math|0}} dan <math display="inline">\frac{\pi}{2}</math> [[radian]] {{math|(90°),}} definisi lingkaran satuan memungkinkan untuk memperluas [[Domain suatu fungsi|domain]] dari fungsi trigonometri ke semua bilangan real positif dan negatif. |
|||
[[Berkas:Unit Circle Definitions of Six Trigonometric Functions.svg|jmpl|300x300px|Pada gambar, ada enam fungsi trigonometri bersudutkan sembarang {{math|''θ''}} yang diwakili sebagai [[Sistem koordinat Kartesius|koordinat Cartesius]] dari titik yang dikaitkan dengan [[lingkaran satuan]]. Masing-masing ordinat {{math|A}}, {{math|B}} dan {{math|D}} merupakan nilai dari {{math|sin ''θ''}}, {{math|tan ''θ''}} dan {{math|csc ''θ''}}, sedangkan masing-masing absis dari {{math|A}}, {{math|C}} dan {{math|E}} merupakan nilai {{math|cos ''θ''}}, {{math|cot ''θ''}} dan {{math|sec ''θ''}}.]] |
|||
Enam fungsi trigonometri dapat didefinisikan sebagai [[Sistem koordinat Kartesius|nilai dari titik koordinat]] di [[bidang Euklides]] yang berkaitan dengan sebuah lingkaran berjari-jari satu yang berpusat di titik asal {{math|O}} dari koordinat sistem, yaitu [[lingkaran satuan]]. Sedangkan [[Pengguna:Dedhert.Jr/Uji halaman 15#Definisi segitiga bersiku|definisi segitiga bersiku]] yang memungkinkan definisi fungsi trigonometri untuk sudut di antara {{math|0}} dan <math display="inline">\frac{\pi}{2}</math> [[radian]] {{math|(90°),}} maka definisi lingkaran satuan memungkinkan bahwa domain dari fungsi trigonometri diperluas untuk semua bilangan real positif dan negatif. |
|||
Misalkan <math>\mathcal L</math> adalah [[Sinar (geometri)|sinar]] yang didapatkan dengan memutarnya setengah sudut positif {{mvar|θ}} dari sumbu-{{math|''x''}} (putarannya berlawanan [[arah jarum jam]] untuk <math>\theta > 0,</math> dan searah jarum jam untuk <math>\theta < 0</math>). Sinar ini memotong lingkaran satuan di titik <math>\mathrm{A} = (x_\mathrm{A},y_\mathrm{A}).</math> Sinar <math>\mathcal L,</math> jika perlu diperpanjang [[Garis (geometri)|garisnya]], memotong garis persamaan <math>x=1</math> di titik <math>\mathrm{B} = (1,y_\mathrm{B}),</math> dan garis persamaan <math>y=1</math> di titik <math>\mathrm{C} = (x_\mathrm{C},1).</math> [[Garis singgung|Garis yang menyinggung]] lingkaran satuan di titik {{math|A}} dikatakan [[Tegak lurus|tegaklurus]] terhadap <math>\mathcal L,</math> serta memotong sumbu-{{math|''y''}} di titik <math>\mathrm{D} = (0,y_\mathrm{D})</math> dan sumbu-{{math|''x''}} di titik <math>\mathrm{E} = (x_\mathrm{E},0).</math> [[Sistem koordinat Kartesius|Koordinat]] dari titik tersebut yang memberikan nilai dari semua fungsi trigonometri untuk setiap nilai real sebarang {{mvar|θ}}, dapat dicari sebagai berikut. |
|||
Fungsi trigonometri {{math|cos}} didefinisikan sebagai nilai koordinat-{{Math|''x''}} dari titik {{math|A}}, sedangkan fungsi trigonometri {{math|sin}} didefinisikan sebagai nilai koordinat-{{Math|''y''}} dari titik {{math|A}}. |
|||
<!--The trigonometric functions {{math|cos}} and {{math|sin}} are defined, respectively, as the ''x''- and ''y''-coordinate values of point {{math|A}}, i.e., |
|||
:<math>\cos \theta = x_\mathrm{A} \quad</math> and <math>\quad \sin \theta = y_\mathrm{A}.</math><ref>{{Cite web|url=https://www.encyclopediaofmath.org/index.php/Trigonometric_functions|title=Trigonometric Functions|last=Bityutskov|first=V.I.|date=2011-02-07|website=Encyclopedia of Mathematics|language=en|archive-url=https://web.archive.org/web/20171229231821/https://www.encyclopediaofmath.org/index.php/Trigonometric_functions|archive-date=2017-12-29|url-status=live|access-date=2017-12-29}}</ref> |
|||
: <math>\cos \theta = x_\mathrm{A} \quad</math> and <math>\quad \sin \theta = y_\mathrm{A}.</math><ref>{{Cite web|last=Bityutskov|first=V.I.|date=7 February 2011|title=Trigonometric Functions|url=https://www.encyclopediaofmath.org/index.php/Trigonometric_functions|website=Encyclopedia of Mathematics|language=en|archive-url=https://web.archive.org/web/20171229231821/https://www.encyclopediaofmath.org/index.php/Trigonometric_functions|archive-date=29 December 2017|access-date=29 December 2017|url-status=live}}</ref> |
|||
In the range <math>0 \le \theta \le \pi/2</math> this definition coincides with the right-angled triangle definition by taking the right-angled triangle to have the unit radius {{math|OA}} as [[hypotenuse]], and since for all points <math>\mathrm{P} = (x,y)</math> on the unit circle the equation <math>x^2+y^2=1</math> holds, this definition of cosine and sine also satisfies the '''Pythagorean identity''' |
|||
:<math>\cos^2\theta+\sin^2\theta=1.</math> |
|||
Dengan kisaran ({{Lang-en|range}}) <math>0 \le \theta \le \pi/2</math>, maka definisi ini bertepatan dengan definisi segitiga sudut siku-siku dengan mengambil segitiga siku-siku agar mempunyai jari-jari lingkaran satuan {{math|OA}} sebagai [[hipotenusa]]. Karena persamaan <math>x^2+y^2=1</math> berlaku untuk semua titik <math>\mathrm{P} = (x,y)</math> pada lingkran satuan, maka definisi kosinus dan sinus ini juga memenuhi [[identitas Pythagoras]]. |
|||
The other trigonometric functions can be found along the unit circle as |
|||
:<math>\tan \theta = y_\mathrm{B} \quad</math> and <math> \quad\cot \theta = x_\mathrm{C},</math> |
|||
:<math>\ |
: <math>\cos^2\theta+\sin^2\theta=1.</math> |
||
Selain kedua fungsi trigonometri di atas, fungsi lainnya dapat ditemukan di sepanjang lingkaran satuan |
|||
: <math>\tan \theta = y_\mathrm{B} \quad</math> dan <math> \quad\cot \theta = x_\mathrm{C},</math> |
|||
: <math>\csc \theta\ = y_\mathrm{D} \quad</math> dan <math> \quad\sec \theta = x_\mathrm{E}.</math> |
|||
Dengan menerapkan identitas Pythagoras dan metode bukti geometri, maka dapat diperlihatkan bahwa definisi ini bertepatan dengan definisi fungsi tangen, kotangen, sekan dan kosekan dalam bentuk fungsi sinus dan kosinus. Dengan kata lain, |
|||
By applying the Pythagorean identity and geometric proof methods, these definitions can readily be shown to coincide with the definitions of tangent, cotangent, secant and cosecant in terms of sine and cosine, that is |
|||
: <math>\tan \theta =\frac{\sin \theta}{\cos\theta},\quad \cot\theta=\frac{\cos\theta}{\sin\theta},\quad \sec\theta=\frac{1}{\cos\theta},\quad \csc\theta=\frac{1}{\sin\theta}.</math> |
: <math>\tan \theta =\frac{\sin \theta}{\cos\theta},\quad \cot\theta=\frac{\cos\theta}{\sin\theta},\quad \sec\theta=\frac{1}{\cos\theta},\quad \csc\theta=\frac{1}{\sin\theta}.</math> |
||
[[ |
[[Berkas:Trigonometric_functions.svg|link={{filepath:trigonometric_functions_derivation_animation.svg}}|ka|jmpl|300x300px|Pada gambar, terdapat fungsi: |
||
{{color|#00A|Sine}}, |
{{color|#00A|Sine}}, |
||
{{color|#0A0|Cosine}}, |
{{color|#0A0|Cosine}}, |
||
{{color|#A00|Tangent}}, |
{{color|#A00|Tangent}}, |
||
{{color|#00A|Cosecant ( |
{{color|#00A|Cosecant (bergaris titik)}}, |
||
{{color|#0A0|Secant ( |
{{color|#0A0|Secant (bergaris titik)}}, |
||
{{color|#A00|Cotangent ( |
{{color|#A00|Cotangent (bergaris titik)}} |
||
– Untuk animasinya, dapat dilihat di [{{filepath:trigonometric_functions_derivation_animation.svg}} sini] ]] |
|||
Karena putaran sudut dari <math>\pm2\pi</math> tidak mengubah posisi atau ukuran bentuk, titik-titik {{math|A}}, {{math|B}}, {{math|C}}, {{math|D}}, dan {{math|E}} adalah sama untuk dua sudut yang mempunyai selisihnya yang berupakan kelipatan bilangan bulat dari <math>2\pi</math>. Jadi, fungsi trigonometri merupakan [[fungsi berkala]] dengan periode <math>2\pi</math>. Artinya, persamaan |
|||
: <math> \sin\theta = \sin\left(\theta + 2 k \pi \right)\quad</math> dan <math>\quad \cos\theta = \cos\left(\theta + 2 k \pi \right)</math> |
|||
As a rotation of an angle of <math>\pm2\pi</math> does not change the position or size of a shape, the points {{math|A}}, {{math|B}}, {{math|C}}, {{math|D}}, and {{math|E}} are the same for two angles whose difference is an integer multiple of <math>2\pi</math>. Thus trigonometric functions are [[periodic function]]s with period <math>2\pi</math>. That is, the equalities |
|||
: <math> \sin\theta = \sin\left(\theta + 2 k \pi \right)\quad</math> and <math>\quad \cos\theta = \cos\left(\theta + 2 k \pi \right)</math> |
|||
hold for any angle {{mvar|θ}} and any [[integer]] {{mvar|k}}. The same is true for the four other trigonometric functions. Observing the sign and the monotonicity of the functions sine, cosine, cosecant, and secant in the four quadrants, shows that {{math|2{{pi}}}} is the smallest value for which they are periodic, i.e., {{math|2{{pi}}}} is the [[periodic function|fundamental period]] of these functions. However, already after a rotation by an angle <math>\pi</math> the points {{mvar|B}} and {{mvar|C}} return to their original position, so that the tangent function and the cotangent function have a fundamental period of {{pi}}. That is, the equalities |
|||
: <math> \tan\theta = \tan(\theta + k\pi) \quad</math> and <math>\quad \cot\theta = \cot(\theta + k\pi)</math> |
|||
hold for any angle {{mvar|θ}} and any integer {{mvar|k}}.--> |
|||
berlaku untuk setiap sudut {{mvar|θ}} dan setiap [[bilangan bulat]] {{mvar|k}}. Hal ini berlaku benar untuk keempat fungsi trigonometri lainnya. Dengan mengamati tanda dan kemonotonan dari fungsi sinus, kosekan, kotangen, dan sekan dalam yang ada di dalam keempat kuadran, maka untuk fungsi-fungsi yang dikatakan periodik dapat diperlihatkan bahwa <math>2\pi</math> merupakan nilai yang paling terkecil (dengan kata lain, <math>2\pi</math> merupakan [[Fungsi berkala|periode dasar]] dari fungsi tersebut). Namun, saat putaran sudut <math>\pi</math>, titik {{mvar|B}} dan {{mvar|C}} telah kembali ke posisi awal sehingga fungsi tangen dan fungsi kotangen mempunyai periode dasar dari <math>\pi</math>. Dengan kata lain, persamaan |
|||
== Nilai aljabar == |
|||
[[Berkas:Unit circle angles color.svg|right|thumb|300px|<!--The [[unit circle]], with some points labeled with their cosine and sine (in this order), and the corresponding angles in radians and degrees.-->]] |
|||
[[Ekspresi aljabar]] untuk sudut terpenting adalah sebagai berikut: |
|||
:<math>\ |
: <math> \tan\theta = \tan(\theta + k\pi) \quad</math> dan <math>\quad \cot\theta = \cot(\theta + k\pi)</math> |
||
:<math>\sin \frac\pi6 = \sin 30^\circ = \frac{\sqrt1}2 = \frac{1}{2}</math> |
|||
:<math>\sin \frac\pi4 = \sin 45^\circ = \frac{\sqrt{2}}{2}</math> |
|||
:<math>\sin \frac\pi3 = \sin 60^\circ = \frac{\sqrt{3}}{2}</math> |
|||
:<math>\sin \frac\pi2 = \sin 90^\circ = \frac{\sqrt4}2 = 1</math> ([[sudut miring]]) |
|||
berlaku untuk setiap sudut {{mvar|θ}} dan setiap bilangan bulat {{mvar|k}}. |
|||
Menulis pembilang sebagai akar kuadrat dari bilangan bulat non-negatif berurutan, dengan penyebut 2, memberikan cara mudah untuk mengingat nilai.<ref name="Larson_2013"/> |
|||
== Nilai aljabar == |
|||
Ekspresi sederhana seperti itu umumnya tidak ada untuk sudut lain yang merupakan kelipatan rasional dari sudut lurus. |
|||
[[Berkas:Unit circle angles color.svg|ka|jmpl|300x300px|Gambar menunjukkan titik-titik dilabeli dengan nilai dari fungsi sinus dan kosinus (sesuai urutannya) di sepanjang [[lingkaran satuan]], dan sudut yang sama dalam radian dan derajat.]] |
|||
Untuk sudut yang diukur dalam derajat, merupakan kelipatan tiga, sinus dan cosinus dapat dinyatakan dalam [[akar kuadrat]] (lihat [[Konstanta trigonometri dinyatakan dalam radikal nyata]]). Dengan demikian, nilai-nilai sinus dan kosinus dapat dibangun oleh [[Konstruksi kompas dan garis lurus|penggaris dan kompas]]. |
|||
[[Bentuk aljabar]] yang berupakan sudut yang sangat penting dinyatakan sebagai berikut: |
|||
: <math>\sin 0 = \sin 0^\circ \quad= \frac{\sqrt0}2 = 0</math> ([[Sudut#Jenis sudut|sudut nol]]) |
|||
Untuk sudut bilangan bulat derajat [[sinus]] dan [[kosinus]] dapat dinyatakan dalam [[akar kuadrat]] dan [[akar pangkat tiga]] dari [[bilangan kompleks]] yang tidak nyata. [[Teori Galois]] memungkinkan untuk membuktikan bahwa jika sudut tersebut bukan kelipatan 3° dari akar pangkat tiga yang tidak nyata tidak dapat dihindari. |
|||
: <math>\sin \frac\pi6 = \sin 30^\circ = \frac{\sqrt1}2 = \frac{1}{2}</math> |
|||
: <math>\sin \frac\pi4 = \sin 45^\circ = \frac{\sqrt{2}}{2} = \frac{1}{\sqrt{2}}</math> |
|||
: <math>\sin \frac\pi3 = \sin 60^\circ = \frac{\sqrt{3}}{2}</math> |
|||
: <math>\sin \frac\pi2 = \sin 90^\circ = \frac{\sqrt4}2 = 1</math> ([[sudut siku-siku]]) |
|||
Dengan menulis pembilang sebagai [[akar kuadrat]] dari bilangan bulat taknegatif berurutan serta penyebutnya adalah 2, maka cara ini dengan mudah mengingat nilai-nilai fungsi trigonometri.<ref name="Larson_2013" /> |
|||
Untuk sudut yang diukur dalam derajat, adalah [[bilangan rasional]], sinus dan kosinus adalah [[bilangan aljabar]], yang dapat diekspresikan dalam istilah [[fungsi akar|{{mvar|n}} fungsi akar]]. Hal tersebut dihasilkan dari [[gugus Galois]] dari [[polinomial siklotom]] adalah gugus [[gugus siklik|siklik]]. |
|||
Namun, bentuk aljabar yang sederhana biasanya tidak ada untuk sudut lainnya yang merupakan kelipatan rasional sudut siku-siku. |
|||
Untuk sudut yang diukur dalam derajat bukan dari bilangan rasional maka sudut dari sinus dan kosinus keduanya adalah [[bilangan transendental]]. Hal tersebut adalah hasil wajar dari [[Teorema Baker]], hal ini dibuktikan pada tahun 1966. |
|||
* Untuk sudut yang diukur dalam satuan derajat merupakan kelipatan dari tiga, [[Nilai trignometri eksak|nilai trigonometri eksak]] dari fungsi sinus dan kosinus dapat dinyatakan dalam bentuk akar kuadrat. Jadi, nilai tersebut dapat dikonstruksi dengan menggunakan [[Konstruksi jangka dan penggaris|penggaris dan jangka]]. |
|||
* Untuk sudut berupa bilangan bulat dalam satuan derajat, nilai dari fungsi sinus dan kosinus dapat dinyatakan dalam bentuk akar kuadrat dan [[akar kubik]] dari [[bilangan kompleks]] takreal. [[Teori Galois]] membuktikan bahwa jika sudut bukan kelipatan dari 3°, maka akar kubik dari bilangan takreal tidak dapat dihindari. |
|||
* Untuk sudut yang dinyatakan dalam satuan derajat adalah [[bilangan rasional]], nilai fungsi sinus dan kosinus merupakan [[bilangan aljabar]] yang dapat dinyatakan dalam bentuk [[Akar ke-|akar ke-{{mvar|n}}]]. Hasil ini berasal dari suatu pernyataan yang mengatakan bahwa [[grup Galois]] dari [[polinomial siklotomik]] dikatakan [[Grup siklik|siklik]]. |
|||
* Untuk sudut yang dinyatakan dalam satuan derajat bukanlah bilangan rasional, maka nilai sudut dari fungsi sinus maupun kosinus merupakan [[bilangan transendental]]. Pernyataan ini merupakan korolari dari [[teorema Baker]] yang dibuktikan pada tahun 1966. |
|||
=== Nilai aljabar sederhana === |
=== Nilai aljabar sederhana === |
||
{{main|Nilai trigonometri eksak#Sudut yang umum}} |
|||
Tabel berikut merangkum nilai aljabar paling sederhana dari fungsi trigonometri.<ref name="Abramowitz and Stegun">Abramowitz, Milton and Irene A. Stegun, p. 74</ref> simbol pada {{math|∞}} mewakili [[titik tak terhingga]] pada [[garis nyata yang diperluas secara proyektif]]; hal ini tidak ditandatangani karena ketika muncul di tabel pada fungsi trigonometri yang sesuai kecenderungan pada nilai {{math|+∞}} di satu sama lain pada nilai {{math|–∞}} di sisi lain, ketika argumen nilai kecenderungan pada tabel. |
|||
Berikut ada sebuah tabel yang memuat kumpulan-kumpulan nilai fungsi sinus, kosinus, dan tangen yang merupakan kelipatan dari 15 derajat, dimulai dari 0 derajat sampai dengan 90 derajat. |
|||
:<math> |
|||
<center> |
|||
\begin{array}{|c|ccccccccc|} |
|||
{| class="wikitable" |
|||
\hline |
|||
!''θ'' dalam satuan radian |
|||
\begin{matrix}\text{Radian}\\ \text{Sudut}\end{matrix} & |
|||
!''θ'' dalam satuan derajat |
|||
\begin{matrix}0\\ 0^\circ\end{matrix} & |
|||
!<math>\sin(\theta)</math> |
|||
\begin{matrix}\frac{\pi}{12}\\ 15^\circ\end{matrix} & |
|||
!<math>\cos(\theta)</math> |
|||
\begin{matrix}\frac{\pi}{8}\\ 22.5^\circ\end{matrix} & |
|||
!<math>\tan(\theta)</math> |
|||
\begin{matrix}\frac{\pi}{6}\\ 30^\circ\end{matrix} & |
|||
|- |
|||
\begin{matrix}\frac{\pi}{4}\\ 45^\circ\end{matrix} & |
|||
|<math>0</math> |
|||
\begin{matrix}\frac{\pi}{3}\\ 60^\circ\end{matrix} & |
|||
|<math>0^\circ</math> |
|||
\begin{matrix}\frac{3\pi}{8}\\ 67.5^\circ\end{matrix} & |
|||
|<math>0</math> |
|||
\begin{matrix}\frac{5\pi}{12}\\ 75^\circ\end{matrix} & |
|||
|<math>1</math> |
|||
\begin{matrix}\frac{\pi}{2}\\ 90^\circ\end{matrix} \\ |
|||
|<math>0</math> |
|||
\hline |
|||
|- |
|||
\sin & |
|||
|<math>\frac{\pi}{12}</math> |
|||
0 & |
|||
|<math>15^\circ</math> |
|||
\frac{ \sqrt{6} - \sqrt{2} } {4} & |
|||
\frac{ |
|<math>\frac{\sqrt{6}-\sqrt{2}}{4}</math> |
||
\frac{ |
|<math>\frac{\sqrt{6}+\sqrt{2}}{4}</math> |
||
|<math>2-\sqrt{3}</math> |
|||
|- |
|||
\frac{\sqrt{3}}{2} & |
|||
\frac{ |
|<math>\frac{\pi}{6}</math> |
||
|<math>30^\circ</math> |
|||
\frac{ \sqrt{6} + \sqrt{2} } {4} & |
|||
|<math>\frac{1}{2}</math> |
|||
1 \\ |
|||
|<math>\frac{\sqrt{3}}{2}</math> |
|||
\cos & |
|||
|<math>\frac{\sqrt{3}}{3}</math> |
|||
1 & |
|||
|- |
|||
\frac{\sqrt{6}+\sqrt{2}}{4} & |
|||
\frac{ |
|<math>\frac{\pi}{4}</math> |
||
|<math>45^\circ</math> |
|||
\frac{\sqrt{3}}{2} & |
|||
\frac{\sqrt{2}}{2} |
|<math>\frac{\sqrt{2}}{2}</math> |
||
\frac{ |
|<math>\frac{\sqrt{2}}{2}</math> |
||
|<math>1</math> |
|||
\frac{ \sqrt{2 - \sqrt{2}} } {2} & |
|||
|- |
|||
\frac{ \sqrt{6} - \sqrt{2}} {4} & |
|||
|<math>\frac{\pi}{3}</math> |
|||
0 \\ |
|||
|<math>60^\circ</math> |
|||
\tan & |
|||
|<math>\frac{\sqrt{3}}{2}</math> |
|||
0 & |
|||
|<math>\frac{1}{2}</math> |
|||
2-\sqrt{3} & |
|||
\sqrt{ |
|<math>\sqrt{3}</math> |
||
|- |
|||
\frac{\sqrt{3}}{3} & |
|||
|<math>\frac{5\pi}{12}</math> |
|||
1 & |
|||
|<math>75^\circ</math> |
|||
\sqrt{3} & |
|||
|<math>\frac{\sqrt{6}+\sqrt{2}}{4}</math> |
|||
\sqrt{2} + 1 & |
|||
|<math>\frac{\sqrt{6}-\sqrt{2}}{4}</math> |
|||
2+\sqrt{3} & |
|||
|<math>2 + \sqrt{3}</math> |
|||
\infty \\ |
|||
|- |
|||
\cot & |
|||
|<math>\frac{\pi}{2}</math> |
|||
\infty & |
|||
|<math>90^\circ</math> |
|||
2+\sqrt{3} & |
|||
|<math>1</math> |
|||
\sqrt{2} + 1 & |
|||
|<math>0</math> |
|||
\sqrt{3} & |
|||
|takterdefinisikan |
|||
1 & |
|||
|} |
|||
\frac{\sqrt{3}}{3} & |
|||
</center> |
|||
\sqrt{2} - 1 & |
|||
2-\sqrt{3} & |
|||
0 \\ |
|||
\sec & |
|||
1 & |
|||
\sqrt{6} - \sqrt{2} & |
|||
\sqrt{2} \sqrt{ 2 - \sqrt{2} } & |
|||
\frac{2\sqrt{3}}{3} & |
|||
\sqrt{2} & |
|||
2 & |
|||
\sqrt{2} \sqrt{ 2 + \sqrt{2} } & |
|||
\sqrt{6}+\sqrt{2} & |
|||
\infty \\ |
|||
\csc & |
|||
\infty & |
|||
\sqrt{6}+\sqrt{2} & |
|||
\sqrt{2} \sqrt{ 2 + \sqrt{2} } & |
|||
2 & |
|||
\sqrt{2} & |
|||
\frac{2\sqrt{3}}{3} & |
|||
\sqrt{2} \sqrt{ 2 - \sqrt{2} } & |
|||
\sqrt{6} - \sqrt{2} & |
|||
1 \\\hline |
|||
\end{array} |
|||
</math> |
|||
== Dalam kalkulus == |
== Dalam kalkulus == |
||
[[Berkas:Trigonometrija-graf.svg|ka|jmpl|[[Grafik fungsi|Grafik]] fungsi sinus, kosinus, dan tangen.]] |
|||
[[Berkas:Taylorsine.svg|thumb|right|Fungsi sinus (biru) sangat dekat dengan fungsi [[Teorema Taylor|polinomial Taylor]] derajat 7 (merah muda) untuk siklus penuh yang berpusat pada asal.]] |
|||
[[Berkas:Taylorsine.svg|ka|jmpl|Grafik fungsi sinus (yang berwarna biru) sangat dihampiri oleh grafik [[Teorema Taylor|polinomial Taylor]] berderajat 7 (yang berwarna merah muda) untuk putaran siklus penuh pada titik asal.]] |
|||
[[Berkas:Taylor cos.gif|thumb|Animasi untuk pendekatan kosinus melalui polinomial Taylor.]] |
|||
[[Berkas:Taylor cos.gif|jmpl|Animasi terkait hampiran kosinus melalui polinomial Taylor.]] |
|||
[[Berkas:Taylorreihenentwicklung des Kosinus.svg|thumb|<math>\cos(x)</math> bersama dengan polinomial Taylor pertama <math>p_n(x)=\sum_{k=0}^n (-1)^k \frac{x^{2k}}{(2k)!}</math>]] |
|||
[[Berkas:Taylorreihenentwicklung des Kosinus.svg|jmpl|Grafik dari <math>\cos(x)</math> dengan polinomial Taylor <math>p_n(x)=\sum_{k=0}^n (-1)^k \frac{x^{2k}}{(2k)!}</math>]] |
|||
Fungsi trigonometri dikatakan [[Fungsi terdiferensialkan|terdiferensialkan]] dan [[Fungsi analitik|analitik]] di setiap titik yang didefinisikannya. Artinya, titik-titik tersebut ada dimana-mana untuk fungsi trigonometri seperti sinus, kosinus. Titik-titik tersebut ada dimana-mana di fungsi tangen, kecuali di {{math|{{pi}}/2 + ''k''{{pi}}}} untuk setiap bilangan bulat {{mvar|k}}. |
|||
Fungsi trigonometri adalah [[fungsi terdiferensiasi|terdiferensiasi]]. Hal ini tidak langsung terbukti dari definisi geometris di atas. Apalagi tren modern dalam matematika. Oleh karena itu, kecuali pada tingkat yang sangat dasar, fungsi trigonometri didefinisikan dengan menggunakan metode kalkulus. |
|||
Fungsi trignometri merupakan [[fungsi berkala]], dan [[Fungsi berkala#Definisi|periode primitif]]<nowiki/>nya bernilai {{math|2{{pi}}}} untuk fungsi sinus dan kosinus, dan {{pi}} untuk fungsi tangen, yang [[Fungsi menaik|naik]] di masing-masing [[selang terbuka]] {{math|({{pi}}/2 + ''k''{{pi}}, {{pi}}/2 + (''k'' + 1){{pi}})}}. Pada masing-masing titik akhir selang tersebut, fungsi tangen mempunyai [[asimtot]] yang mengarah vertikal. |
|||
Untuk menentukan fungsi trigonometri di dalam kalkulus, ada dua kemungkinan yang setara, baik menggunakan [[deret pangkat]] atau [[persamaan diferensial]]. Definisi tersebut setara, karena mulai dari salah satunya, mudah untuk mengambil yang lain sebagai properti. Namun definisi melalui persamaan diferensial entah bagaimana lebih alami, karena, misalnya, pilihan koefisien deret pangkat mungkin tampak cukup sewenang-wenang, dan [[identitas Pythagoras]] jauh lebih mudah untuk disimpulkan dari persamaan diferensial. |
|||
Dalam kalkulus, fungsi trigonometri dapat didefinisikan dengan menggunakan [[deret kuasa]] ataupun [[persamaan diferensial]]. Namun, menggunakan persamaan diferensial terasa lebih alami saat mendefinisikan fungsi trigonometri, karena, sebagai contoh, pemilihan koefisien dari deret kuasa dapat muncul sebagai bilangan yang cukup sebarang, dan persamaan diferensial juga cukup mudah menyimpulkan identitas Pythagoras. |
|||
===Definisi dengan persamaan diferensial=== |
|||
=== Definisi dengan menggunakan persamaan diferensial === |
|||
Sinus dan kosinus adalah [[fungsi terdiferensiasi]] yang unik sedemikian rupa, yaitu |
|||
Fungsi sinus dan kosinus dapat didefinisikan sebagai penyelesaian tunggal untuk [[masalah nilai awal]]: |
|||
:<math> |
|||
\begin{align} |
|||
\frac{d}{dx}\sin x&= \cos x,\\ |
|||
\frac{d}{dx}\cos x&= -\sin x,\\ |
|||
\sin 0&=0,\\ |
|||
\cos 0&=1. |
|||
\end{align} |
|||
</math> |
|||
: <math>\frac{d}{dx}\sin x= \cos x,\ \frac{d}{dx}\cos x= -\sin x,\ \sin(0)=0,\ \cos(0)=1. </math> |
|||
Diferensialkan persamaan tersebut agar orang mengetahui bahwa sinus dan kosinus adalah solusi dari [[persamaan diferensial]] |
|||
:<math>y''+y=0.</math> |
|||
Dengan menurunkannya lagi, maka diperoleh <math display="inline">\frac{d^2}{dx^2}\sin x = \frac{d}{dx}\cos x = -\sin x</math> dan <math display="inline">\frac{d^2}{dx^2}\cos x = -\frac{d}{dx}\sin x = -\cos x</math>. Jadi, fungsi sinus dan kosinus merupakan penyelesaian untuk [[persamaan diferensial biasa]] |
|||
Menerapkan [[aturan hasil bagi]] ke definisi garis singgung sebagai hasil bagi dari sinus oleh kosinus, kita dapat mengetahui bahwa fungsi tangen memverifikasi |
|||
:<math>\frac{d}{dx}\tan x = 1+\tan^2 x.</math> |
|||
: <math>y''+y=0.</math> |
|||
===Ekspansi deret pangkat=== |
|||
Menerapkan persamaan diferensial ke [[deret pangkat]] dengan koefisien tak tentu, seseorang dapat menyimpulkan [[relasi pengulangan]] s untuk koefisien [[deret Taylor]] dari sinus dan kosinus fungsi. Relasi pengulangan tersebut mudah terpecahkan dan memberikan perluasan rangkaian<ref>Lihat Ahlfors, pp. 43–44.</ref> |
|||
Fungsi tangen <math>\tan x = \sin x / \cos x</math> dapat diturunkan dengan menerapkan [[Aturan hasil-bagi|aturan hasil bagi]] dari, maka |
|||
:<math> |
|||
: <math>\frac{d}{dx}\tan x = \frac{\cos^2 x + \sin^2 x}{\cos^2 x} = 1+\tan^2 x.</math> |
|||
=== Perluasan deret pangkat === |
|||
Dengan menerapkan persamaan diferensial untuk [[deret pangkat]] dengan koefisien yang belum ditentukan, maka fungsi sinus dan kosinus dapat disimpulkan sebagai [[relasi rekurensi]] mengenai koefisien [[deret Taylor]] dari kedua fungsi tersebut. Relasi rekurensinya dapat diselesaikan dengan mudah serta memberikan perluasan deret<ref>See Ahlfors, pp. 43–44.</ref> |
|||
: <math> |
|||
\begin{align} |
\begin{align} |
||
\sin x & = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \\[ |
\sin x & = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \\[6mu] |
||
& = \sum_{n=0}^\infty \frac{(-1)^n |
& = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}x^{2n+1} \\[8pt] |
||
\cos x & = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots \\[ |
\cos x & = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots \\[6mu] |
||
& = \sum_{n=0}^\infty \frac{(-1)^n |
& = \sum_{n=0}^\infty \frac{(-1)^n}{(2n)!}x^{2n}. |
||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
[[ |
[[Ruji kekonvergenan]] dari deret tersebut adalah takhingga. Jadi, fungsi sinus dan kosinus dapat diperluas menjadi [[fungsi menyeluruh]], atau fungsi ini disebut "sinus" dan "kosinus"), karena (berdasarkan definisi) fungsi tersebut merupakan [[fungsi bernilai kompleks]] yang terdefinisi dan [[holomorfik]] di seluruh [[bidang kompleks]]. |
||
Ketika kedua fungsi tersebut didefinisikan sebagai pecahan dari fungsi menyeluruh, fungsi trigonometri lainnya dapat diperluas menjadi [[fungsi meromorfik]]. Hal ini mengartikan bahwa fungsi adalah holomorfik di seluruh bidang kompleks, kecuali ada setiap titik terpencil yang disebut [[Nol dan kutub|kutub]]. Disini, kutubnya merupakan bilangan-bilangan dari bentuk <math display="inline">(2k+1)\frac \pi 2</math> untuk fungsi tangen dan fungsi sekan, atau <math>k\pi</math> untuk fungsi kotangen dan fungsi kosekan, dengan {{mvar|k}} adalah bilangan bulat sebarang. |
|||
Relasi |
Relasi rekurensi juga dapat dihitung untuk koefisien [[deret Taylor]] dari fungsi trigonometri lain. Deret-deret ini mempunyai [[ruji kekonvergenan]] terhingga. Koefisiennya mempunyai pandangan [[Kombinatorik|kombinatorial]], yang mengatakan bahwa koefisiennya menghitung [[permutasi selang-seling]] dari himpunan hingga.<ref>Stanley, Enumerative Combinatorics, Vol I., p. 149</ref> Lebih tepatnya, dengan mendefinisikan {{mvar|U<sub>n</sub>}} adalah [[Permutasi selang-seling|bilangan atas/bawah]] ke-{{mvar|n}}, {{mvar|B<sub>n</sub>}} adalah [[bilangan Bernoulli]] ke-{{mvar|n}}, dan {{mvar|E<sub>n</sub>}} adalah [[bilangan Euler]] ke-{{mvar|n}}, maka ada empat perluasan deret berikut didapatkan.<ref>Abramowitz; Weisstein.</ref> |
||
Lebih tepatnya anda dapat mendefinisikan, yaitu |
|||
: {{mvar|U<sub>n</sub>}}, {{mvar|n}} adalah [[angka atas/bawah]], |
|||
: {{mvar|B<sub>n</sub>}}, {{mvar|n}} [[nomor Bernoulli]], dan |
|||
: {{mvar|E<sub>n</sub>}}, adalah {{mvar|n}} [[nomor Euler]], |
|||
satu memiliki ekspansi seri berikut:<ref>Abramowitz; Weisstein.</ref> |
|||
: <math> |
: <math> |
||
\begin{align} |
\begin{align} |
||
\tan x & {} = \sum_{n=0}^\infty \frac{U_{2n+1} |
\tan x & {} = \sum_{n=0}^\infty \frac{U_{2n+1}}{(2n+1)!}x^{2n+1} \\[8mu] |
||
& {} = \sum_{n=1}^\infty \frac{(-1)^{n-1} 2^{2n} \left(2^{2n}-1\right) B_{2n} |
& {} = \sum_{n=1}^\infty \frac{(-1)^{n-1} 2^{2n} \left(2^{2n}-1\right) B_{2n}}{(2n)!}x^{2n-1} \\[5mu] |
||
& {} = x + \frac{1}{3}x^3 + \frac{2}{15}x^5 + \frac{17}{315}x^7 + \cdots, \qquad \text{ |
& {} = x + \frac{1}{3}x^3 + \frac{2}{15}x^5 + \frac{17}{315}x^7 + \cdots, \qquad \text{untuk } |x| < \frac{\pi}{2}. |
||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| Baris 318: | Baris 261: | ||
: <math> |
: <math> |
||
\begin{align} |
\begin{align} |
||
\csc x & |
\csc x &= \sum_{n=0}^\infty \frac{(-1)^{n+1} 2 \left(2^{2n-1}-1\right) B_{2n}}{(2n)!}x^{2n-1} \\[5mu] |
||
& |
&= x^{-1} + \frac{1}{6}x + \frac{7}{360}x^3 + \frac{31}{15120}x^5 + \cdots, \qquad \text{untuk } 0 < |x| < \pi. |
||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| Baris 325: | Baris 268: | ||
: <math> |
: <math> |
||
\begin{align} |
\begin{align} |
||
\sec x & |
\sec x &= \sum_{n=0}^\infty \frac{U_{2n}}{(2n)!}x^{2n} |
||
= \sum_{n=0}^\infty \frac{(-1)^n E_ |
= \sum_{n=0}^\infty \frac{(-1)^n E_{2n}}{(2n)!}x^{2n} \\[5mu] |
||
& |
&= 1 + \frac{1}{2}x^2 + \frac{5}{24}x^4 + \frac{61}{720}x^6 + \cdots, \qquad \text{untuk } |x| < \frac{\pi}{2}. |
||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| Baris 333: | Baris 276: | ||
: <math> |
: <math> |
||
\begin{align} |
\begin{align} |
||
\cot x & |
\cot x &= \sum_{n=0}^\infty \frac{(-1)^n 2^{2n} B_{2n}}{(2n)!}x^{2n-1} \\[5mu] |
||
& |
&= x^{-1} - \frac{1}{3}x - \frac{1}{45}x^3 - \frac{2}{945}x^5 - \cdots, \qquad \text{untuk } 0 < |x| < \pi. |
||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
=== Perluasan pecahan berlanjut === |
|||
Terdapat representasi deret sebagai [[ekspansi pecahan parsial]] yang baru saja diterjemahkan dari [[Pembalikan perkalian|fungsi timbal balik]] dijumlahkan, sehingga [[Pole (analisis kompleks)|pole]] dari fungsi kotangen dan fungsi timbal balik cocok:<ref name="Aigner_2000"/> |
|||
Perluasan pecahan berlanjut berikut valid di seluruh bidang kompleks: |
|||
: <math> \sin x = |
|||
\cfrac{x}{1 + \cfrac{x^2}{2\cdot3-x^2 + |
|||
\cfrac{2\cdot3 x^2}{4\cdot5-x^2 + |
|||
\cfrac{4\cdot5 x^2}{6\cdot7-x^2 + \ddots}}}}</math> |
|||
: <math> \cos x = \cfrac{1}{1 + \cfrac{x^2}{1 \cdot 2 - x^2 + \cfrac{1 \cdot 2x^2}{3 \cdot 4 - x^2 + \cfrac{3 \cdot 4x^2}{5 \cdot 6 - x^2 + \ddots}}}}</math> |
|||
: <math>\tan x = \cfrac{x}{1 - \cfrac{x^2}{3 - \cfrac{x^2}{5 - \cfrac{x^2}{7 - \ddots}}}}=\cfrac{1}{\cfrac{1}{x} - \cfrac{1}{\cfrac{3}{x} - \cfrac{1}{\cfrac{5}{x} - \cfrac{1}{\cfrac{7}{x} - \ddots}}}}</math> |
|||
Pecahan yang terakhir dipakai pertama kali menurut sejarah dalam [[bukti bahwa π irasional]].<ref>{{citation|editor1-last=Berggren|editor1-first=Lennart|editor2-last=Borwein|editor2-first=Jonathan M.|editor2-link=Jonathan M. Borwein|editor3-last=Borwein|editor3-first=Peter B.|editor3-link=Peter B. Borwein|last=Lambert|first=Johann Heinrich|orig-year=1768|chapter=Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques|title=Pi, a source book|place=New York|publisher=[[Springer Science+Business Media|Springer-Verlag]]|year=2004|edition=3rd|pages=129–140|isbn=0-387-20571-3}}</ref> |
|||
<!--=== Perluasan pecahan parsial === |
|||
There is a series representation as [[partial fraction expansion]] where just translated [[Multiplicative inverse|reciprocal functions]] are summed up, such that the [[Pole (complex analysis)|poles]] of the cotangent function and the reciprocal functions match:<ref name="Aigner_2000" /> |
|||
: <math> |
: <math> |
||
\pi \cot \pi x = \lim_{N\to\infty}\sum_{n=-N}^N \frac{1}{x+n}. |
\pi \cot \pi x = \lim_{N\to\infty}\sum_{n=-N}^N \frac{1}{x+n}. |
||
</math> |
</math> |
||
This identity can be proven with the [[Gustav Herglotz|Herglotz]] trick.<ref name="Remmert_1991"/> |
|||
This identity can be proven with the [[Gustav Herglotz|Herglotz]] trick.<ref name="Remmert_1991" /> Combining the {{math|(–''n'')}}th with the {{math|''n''}}th term lead to [[Absolute convergence|absolutely convergent]] series: |
|||
Menggabungkan nilai {{math|(–''n'')}} ke nilai {{math|''n''}}istilah tersebut mengarah pada rangkaian [[konvergensi absolut|konvergen]], yaitu: |
|||
:<math> |
|||
: <math> |
|||
\pi \cot \pi x = \frac{1}{x} + 2x\sum_{n=1}^\infty \frac{1}{x^2-n^2}\ , \quad \frac{\pi}{\sin \pi x} = \frac{1}{x} + 2x\sum_{n=1}^\infty \frac{(-1)^n}{x^2-n^2}. |
|||
\pi \cot \pi x = \frac{1}{x} + 2x\sum_{n=1}^\infty \frac{1}{x^2-n^2}. |
|||
</math> |
</math> |
||
Similarly, one can find a partial fraction expansion for the secant, cosecant and tangent functions: |
|||
===Ekspansi produk tanpa batas=== |
|||
Produk tak terbatas berikut untuk sinus sangat penting dalam analisis kompleks, yaitu: |
|||
:<math>\sin z=z\displaystyle\prod_{n=1}^\infty \left(1-\frac{z^2}{n^2 \pi^2}\right), \quad z\in\mathbb C.</math> |
|||
Untuk bukti pemuaian (lihat [[Sinus#Pecahan parsial dan ekspansi hasil kali sinus kompleks|Sinus]]). Dari sini, dapat disimpulkan bahwa |
|||
:<math>\cos z=\displaystyle\prod_{n=1}^\infty \left(1-\frac{z^2}{\left(n-\frac12\right)^2 \pi^2}\right), \quad z\in\mathbb C.</math> |
|||
: <math> |
|||
===Hubungan dengan fungsi eksponensial (Rumus Euler)=== |
|||
\pi\csc\pi x = \sum_{n=-\infty}^\infty \frac{(-1)^n}{x+n}=\frac{1}{x} + 2x\sum_{n=1}^\infty \frac{(-1)^n}{x^2-n^2}, |
|||
[[Berkas:Sinus und Kosinus am Einheitskreis 3.svg|thumb|<math>\cos(\theta)</math> dan <math>\sin(\theta)</math> adalah bagian nyata dan imajiner pada nilai <math>e^{i\theta}</math>.]] |
|||
</math> |
|||
: <math>\pi^2\csc^2\pi x=\sum_{n=-\infty}^\infty \frac{1}{(x+n)^2},</math> |
|||
: <math> |
|||
\pi\sec\pi x = \sum_{n=0}^\infty (-1)^n \frac{(2n+1)}{(n+\tfrac12)^2 - x^2}, |
|||
</math> |
|||
: <math> |
|||
\pi \tan \pi x = 2x\sum_{n=0}^\infty \frac{1}{(n+\tfrac12)^2 - x^2}. |
|||
</math>--> |
|||
=== Perluasan darab takhingga === |
|||
[[Rumus Euler]] menghubungkan sinus dan kosinus dengan [[fungsi eksponensial]]: |
|||
Darab takhingga untuk fungsi sinus sangat penting dalam [[analisis kompleks]], yang dinyatakan sebagai: |
|||
:<math> e^{ix} = \cos x + i\sin x. </math> |
|||
Rumus ini biasanya dianggap untuk nilai nyata dari {{mvar|x}}, tetapi tetap benar untuk semua nilai kompleks. |
|||
: <math>\sin z = z \prod_{n=1}^\infty \left(1-\frac{z^2}{n^2 \pi^2}\right), \quad z\in\mathbb C.</math> |
|||
''Bukti'': Jika nilai <math>f_1(x)=\cos x + i\sin x,</math> dan <math>f_2(x)=e^{ix}.</math> dan memiliki nilai <math display="inline">\frac{d}{dx}f_j(x)= if_j(x)</math> dari {{math|1=''j'' = 1, 2}}. [[Aturan hasil bagi]] menyiratkan demikian <math display="inline">\frac{d}{dx}\left(\frac{f_1(x)}{f_2(x)}\right)=0</math>. Karena itu, <math display="inline">\frac{f_1(x)}{f_2(x)}</math> adalah fungsi konstan yang sama pada nilai {{val|1}}, sebagai nilai <math>f_1(0)=f_2(0)=1.</math> Hal ini membuktikan rumusnya. |
|||
Bukti perluasan darab ini dapat dilihat di[[Sinus dan kosinus#Pecahan parsial dan perluasan darab sinus kompleks|sin]]<nowiki/>i. Melalui rumus ini, dapat disimpulkan bahwa |
|||
Hal ini memiliki rumus: |
|||
:<math>\begin{align} |
|||
: <math>\cos z = \prod_{n=1}^\infty \left(1-\frac{z^2}{(n-1/2)^2 \pi^2}\right), \quad z\in\mathbb C.</math> |
|||
e^{ix} &= \cos x + i\sin x\\[5pt] |
|||
e^{-ix} &= \cos x - i\sin x. |
|||
=== Kaitan dengan rumus Euler === |
|||
\end{align}</math> |
|||
[[Berkas:Sinus und Kosinus am Einheitskreis 3.svg|jmpl|<math>\cos(\theta)</math> and <math>\sin(\theta)</math> are the real and imaginary part of <math>e^{i\theta}</math> respectively.]] |
|||
[[Rumus Euler]] mengaitkan fungsi sinus dan kosinus dengan [[fungsi eksponensial]]: |
|||
: <math> e^{ix} = \cos x + i\sin x.</math> |
|||
Rumus ini biasanya dipandang untuk bilangan real {{mvar|x}}, tetapi tetap benar untuk semua bilangan kompleks. Rumus ini dapat dibuktikan sebagai berikut: Misalkan <math>f_1(x)=\cos x + i\sin x</math> dan <math>f_2(x)=e^{ix}</math>. Karena <math>df_j(x)/dx= if_j(x)</math> untuk {{math|1=''j'' = 1, 2}}, maka menurut kaidah [[Kaidah hasil-bagi|hasil bagi]], <math>d/dx\, (f_1(x)/f_2(x))=0</math>. Jadi, <math>f_1(x)/f_2(x)</math> adalah fungsi konstan, yang sama dengan {{val|1}}, ketika <math>f_1(0)=f_2(0)=1.</math> Hal ini membuktikan rumus tersebut. |
|||
Selanjutnya, didapatkan persamaan <math>e^{ix} = \cos x + i\sin x</math> dan <math>e^{-ix} = \cos x - i\sin x</math>. Dengan menyelesaikan [[sistem linear]] pada fungsi sinus dan kosinus, maka dapat dinyatakan dalam bentuk fungsi eksponensial: |
|||
Memecahkan [[sistem linier]] tersebut dalam sinus dan kosinus, seseorang dapat mengekspresikannya dalam fungsi eksponensial: |
|||
: <math>\begin{align}\sin x &= \frac{e^{i x} - e^{-i x}}{2i}\\[5pt] |
: <math>\begin{align}\sin x &= \frac{e^{i x} - e^{-i x}}{2i}\\[5pt] |
||
\cos x &= \frac{e^{i x} + e^{-i x}}{2}. |
\cos x &= \frac{e^{i x} + e^{-i x}}{2}. |
||
\end{align}</math> |
\end{align}</math> |
||
Ketika {{mvar|x}} adalah bilangan real, kedua fungsi tersebut dapat ditulis ulang sebagai |
|||
: <math>\cos x = \operatorname{Re}\left(e^{i x}\right), \qquad \sin x = \operatorname{Im}\left(e^{i x}\right).</math> |
: <math>\cos x = \operatorname{Re}\left(e^{i x}\right), \qquad \sin x = \operatorname{Im}\left(e^{i x}\right).</math> |
||
Hampir [[Daftar identitas trigonometri|identitas trigonometri]] dapat dibuktikan dengan memnyatakan fungsi trigonometri dalam bentuk fungsi eksponensial kompleks melalui rumus di atas, dan kemudian menggunakan identitas <math>e^{a+b}=e^ae^b</math> untuk menyederhanakan hasilnya. |
|||
===Definisi menggunakan persamaan fungsional=== |
=== Definisi yang menggunakan persamaan fungsional === |
||
Fungsi trigonometri dapat didefinisikan dengan menggunakan berbagai [[persamaan fungsional]]. |
Fungsi trigonometri juga dapat didefinisikan dengan menggunakan berbagai [[persamaan fungsional]]. Sebagai contoh,<ref name="Kannappan_2009" /> fungsi sinus dan kosinus membentuk pasangan tunggal dari [[fungsi kontinu]] yang memenuhi rumus selisih. |
||
Sebagai contoh,<ref name="Kannappan_2009"/> sinus dan kosinus membentuk pasangan unik [[fungsi kontinu]] s yang memenuhi rumus selisih |
|||
: <math>\cos(x- y) = \cos x\cos y + \sin x\sin y\,</math> |
: <math>\cos(x- y) = \cos x\cos y + \sin x\sin y\,</math> |
||
and the added condition |
|||
: <math>0 < x\cos x < \sin x < x\quad\text{ dari }\quad 0 < x < 1.</math> |
|||
dan ditambah dengan syarat |
|||
===Di bidang kompleks=== |
|||
Sinus dan kosinus dari sebuah [[bilangan kompleks]] <math>z=x+iy</math> dapat diekspresikan dalam bentuk sinus, kosinus, dan [[fungsi hiperbolik]] nyata sebagai berikut: |
|||
: <math>0 < x\cos x < \sin x < x\quad\text{ untuk }\quad 0 < x < 1.</math> |
|||
=== Dalam bidang kompleks === |
|||
Fungsi sinus dan kosinus dari [[bilangan kompleks]] <math>z=x+iy</math> dapat dinyatakan dalam bentuk fungsi sinus, kosinus, dan [[Fungsi hiperbolik|hiperbolik]] sebagai berikut: |
|||
: <math>\begin{align}\sin z &= \sin x \cosh y + i \cos x \sinh y\\[5pt] |
: <math>\begin{align}\sin z &= \sin x \cosh y + i \cos x \sinh y\\[5pt] |
||
\cos z &= \cos x \cosh y - i \sin x \sinh y\end{align}</math> |
\cos z &= \cos x \cosh y - i \sin x \sinh y\end{align}</math> |
||
Grafik fungsi trigonometri sebagai fungsi bernilai kompleks dapat digambarkan dengan memanfaatkan [[pewarnaan domain]]. Berbagai tampilan fungsi yang unik hingga fungsi kompleks dapat dilhat dari grafik; contohnya dapat dilihat bahwa fungsi sinus dan kosinus menjadi tidak terbatas ketika bagian imajiner <math>z</math> semakin besar (dengan warna putih menyatakan takhingga), dan fungsi yang memuat [[Pole (matematika)|pole]] sederhana rupanya merupakan warna yang berputar di sekitar nol atau kutub sekali. Grafik-grafik di bawah yang dibandingkan dengan fungsi hiperbolik yang berpadanan memperlihatkan kaitan antara kedua fungsi tersebut. |
|||
{| style="text-align:center" |
{| style="text-align:center" |
||
|+ |
|+'''Fungsi trigonometri dalam bidang kompleks''' |
||
|[[Berkas: |
|[[Berkas:Trig-sin.png|thumb]] |
||
<math> |
|||
|[[Berkas:Complex cos.jpg|1000x136px|none]] |
|||
|[[Berkas:Complex tan.jpg|1000x136px|none]] |
|||
|[[Berkas:Complex Cot.jpg|1000x136px|none]] |
|||
|[[Berkas:Complex Sec.jpg|1000x136px|none]] |
|||
|[[Berkas:Complex Csc.jpg|1000x136px|none]] |
|||
|- |
|||
|<math> |
|||
\sin z\, |
\sin z\, |
||
</math> |
</math> |
||
[[Berkas:Trig-cos.png|thumb]] |
|||
|<math> |
|||
<math> |
|||
\cos z\, |
\cos z\, |
||
</math> |
</math> |
||
|[[Berkas:Trig-tan.png|thumb]] |
|||
|<math> |
|||
<math> |
|||
\tan z\, |
\tan z\, |
||
</math> |
</math> |
||
[[Berkas:Trig-cot.png|thumb]] |
|||
|<math> |
|||
<math> |
|||
\cot z\, |
\cot z\, |
||
</math> |
</math> |
||
|[[Berkas:Trig-sec.png|thumb]] |
|||
|<math> |
|||
<math> |
|||
\sec z\, |
\sec z\, |
||
</math> |
</math> |
||
[[Berkas:Trig-csc.png|thumb]] |
|||
|<math> |
|||
<math> |
|||
\csc z\, |
\csc z\, |
||
</math> |
</math> |
||
|} |
|} |
||
== Identitas dasar == |
|||
[[Identitas (matematika)|Identitas]] yang berhubungan dengan fungsi trigonometri merupakan bagian dari dasar untuk lebih banyak identitas (lihat [[Daftar identitas trigonometri]]). Identitas tersebut dapat dibuktikan secara geometris dari definisi lingkaran satuan atau definisi segitiga siku-siku (meskipun untuk definisi yang terakhir hati-hati anda harus diberikan untuk sudut yang tidak dalam interval {{math|[0, {{pi}}/2]}}, lihat [[Bukti identitas trigonometri]]). Untuk pembuktian non-geometris yang hanya menggunakan perkakas [[kalkulus]], seseorang dapat menggunakan persamaan diferensial secara langsung, dengan cara yang mirip dengan [[#Hubungan dengan fungsi eksponensial (Rumus Euler)|bukti]] identitas Euler. Anda juga dapat menggunakan identitas Euler untuk mengekspresikan semua fungsi trigonometri dalam istilah eksponensial kompleks dan menggunakan properti fungsi eksponensial. |
|||
== |
==Identitas dasar== |
||
Ada banyak [[Identitas (matematika)|identitas]] yang saling berhubungan dengan fungsi trigonometri. Bagian ini memuat identitas yang paling dasar; identitas yang lebih banyak dapat lihat di [[Daftar identitas trigonometri]]. Identitas berikut dapat dibuktikan secara geometri mellaui definisi lingkaran satuan atau definisi bersudut siku-siku (walauapun definisi terakhir harus mengambil sudut yang bukan berada di dalam interval {{math|[0, {{pi}}/2]}}, lihat [[Bukti identitas trigonometri]]). Bukti tanpa geometri, yakni hanya dengan menggunakan alat [[kalkulus]], dapat dipakai menggunakan persamaan diferensial langsung, melalui cara yang mirip dengan [[#Kaitan dengan rumus Euler|bukti sebelumnya]]. Selain itu, buktinya dapat menggunakan identitas Euler pula untuk menyatakan semua fungsi trigonometri dalam benetuk eksponensial kompleks beserta menggunakan sifat-sifat fungsi eksponensial. |
|||
Kosinus dan garis potongan adalah [[fungsi genap]]; fungsi trigonometri lainnya adalah [[fungsi ganjil]]. Rumus nya adalah: |
|||
:<math>\begin{align} |
|||
===Paritas=== |
|||
\sin(-x) &=-\sin x\\ |
|||
Fungsi kosinus dan sekan merupakan [[fungsi genap]], sedangkan fungsi trigonometri lain merupakan [[fungsi ganjil]]. Paritas dari fungsi-fungsi ini ditulis sebagai berikut: |
|||
\cos(-x) &=\cos x\\ |
|||
{{div col|colwidth=30em}} |
|||
\tan(-x) &=-\tan x\\ |
|||
\ |
:<math> \sin(-x) =-\sin x </math> |
||
\ |
:<math> \cos(-x) =\cos x </math> |
||
\ |
:<math> \tan(-x) =-\tan x </math> |
||
\ |
:<math> \cot(-x) =-\cot x </math> |
||
:<math> \csc(-x) =-\csc x </math> |
|||
:<math>\sec(-x) =\sec x </math> |
|||
{{div col end}} |
|||
===Periode=== |
===Periode=== |
||
Semua fungsi trigonometri |
Semua fungsi trigonometri merupakan [[fungsi periode]]. Fungsi-fungsi tersebut mempunyai periode yang paling terkecil {{math|2{{pi}}}}, kecuali untuk fungsi tangen dan kotangen yang mempunyai {{pi}} sebagai periode yang paling terkecil. Hal ini mengartikan bahwa untuk setiap bilangan bulat {{mvar|k}}, maka diperoleh: |
||
{{div col|colwidth=30em}} |
|||
:<math>\begin{align} |
|||
\sin (x+2k\pi) |
:<math>\sin (x+2k\pi) =\sin x</math> |
||
\cos (x+2k\pi) |
:<math>\cos (x+2k\pi) =\cos x</math> |
||
\tan (x+k\pi) |
:<math>\tan (x+k\pi) =\tan x</math> |
||
\cot (x+k\pi) |
:<math>\cot (x+k\pi) =\cot x</math> |
||
\csc (x+2k\pi) |
:<math>\csc (x+2k\pi) =\csc x</math> |
||
\sec (x+2k\pi) |
:<math>\sec (x+2k\pi) =\sec x</math> |
||
{{div col end}} |
|||
\end{align}</math> |
|||
===Identitas Pythagoras=== |
===Identitas Pythagoras=== |
||
Identitas Pythagoras merupakan ekspresi [[teorema Pythagoras]] yang berupa fungsi trigonometri. Identitasnya adalah |
|||
[[Identitas Pythagoras]], adalah ekspresi dari [[Teorema Pythagoras]] dalam hal fungsi trigonometri. ini |
|||
:<math>\sin^2 x + \cos^2 x = 1 . </math> |
:<math>\sin^2 x + \cos^2 x = 1 . </math> |
||
===Rumus |
===Rumus jumlah dan selisih=== |
||
Rumus |
Rumus jumlah dan selisih dapat memperluas fungsi sinus, kosinus, dan tangen dari jumlah atau selisih dari dua sudut yang dipandang sebagai fungsi sinus dan kosinus dan tangen dari sudut tersendiri. Rumus-rumus ini dapat diturunkan melalui geometri, berdasarkan argumen [[Ptolemaus]]. Selain itu, rumus ini juga dapat diturunkan secara aljabar menggunakan [[rumus Euler]]. |
||
; Penjumlahan |
|||
; Jumlah |
|||
:<math>\begin{align} |
:<math>\begin{align} |
||
\sin\left(x+y\right)&=\sin x \cos y + \cos x \sin y,\\ |
\sin\left(x+y\right)&=\sin x \cos y + \cos x \sin y,\\[5mu] |
||
\cos\left(x+y\right)&=\cos x \cos y - \sin x \sin y,\\ |
\cos\left(x+y\right)&=\cos x \cos y - \sin x \sin y,\\[5mu] |
||
\tan(x + y) &= \frac{\tan x + \tan y}{1 - \tan x\tan y}. |
\tan(x + y) &= \frac{\tan x + \tan y}{1 - \tan x\tan y}. |
||
\end{align}</math> |
\end{align}</math> |
||
; Selisih |
|||
; Perbedaan |
|||
:<math>\begin{align} |
:<math>\begin{align} |
||
\sin\left(x-y\right)&=\sin x \cos y - \cos x \sin y, |
\sin\left(x-y\right)&=\sin x \cos y - \cos x \sin y,\\[5mu] |
||
\cos\left(x-y\right)&=\cos x \cos y + \sin x \sin y,\\ |
\cos\left(x-y\right)&=\cos x \cos y + \sin x \sin y,\\[5mu] |
||
\tan(x - y) &= \frac{\tan x - \tan y}{1 + \tan x\tan y}. |
\tan(x - y) &= \frac{\tan x - \tan y}{1 + \tan x\tan y}. |
||
\end{align}</math> |
\end{align}</math> |
||
Ketika dua sudut sama, rumus penjumlahan |
Ketika dua sudut adalah sama, maka rumus penjumlahan mereduksi ke persamaan yang lebih sederhana, yang dikenal sebagai [[rumus rangkap dua]]. |
||
:<math>\begin{align} |
:<math>\begin{align} |
||
\sin 2x &= 2 \sin x \cos x = \frac{2\tan x}{1+\tan^2 x}, \\ |
\sin 2x &= 2 \sin x \cos x = \frac{2\tan x}{1+\tan^2 x}, \\[5mu] |
||
\cos 2x &= \cos^2 x - \sin^2 x = 2 \cos^2 x - 1 = 1 - 2 \sin^2 x = \frac{1-\tan^2 x}{1+\tan^2 x},\\ |
\cos 2x &= \cos^2 x - \sin^2 x = 2 \cos^2 x - 1 = 1 - 2 \sin^2 x = \frac{1-\tan^2 x}{1+\tan^2 x},\\[5mu] |
||
\tan 2x &= \frac{2\tan x}{1-\tan^2 x}. |
\tan 2x &= \frac{2\tan x}{1-\tan^2 x}. |
||
\end{align}</math> |
\end{align}</math> |
||
Identitas |
Identitas tersebut dapat dipakai untuk menurunkan [[identitas darab-ke-jumlah]]. |
||
Dengan memisalkan <math>t=\tan \tfrac12 \theta</math>, maka semua fungsi trigonometri dari <math>\theta</math> dapat dinyatakan sebagai [[pecahan rasional]] dari <math>t</math>: |
|||
:<math>\sin \theta = \frac{2t}{1+t^2}, \cos \theta = \frac{1-t^2}{1+t^2}, \tan \theta = \frac{2t}{1-t^2}, d\theta = \frac{2}{1+t^2} \, dt.</math> |
|||
:<math>\begin{align} |
|||
Fungsi yang terakhir merupakan [[substitusi setengah sudut tangen]], yang dipakai untuk membantu perhitungan [[integral]] dari fungsi trigonometri lain menjadi [[fungsi rasional]] tersebut. |
|||
\sin \theta &= \frac{2t}{1+t^2}, \\ |
|||
\cos \theta &= \frac{1-t^2}{1+t^2},\\ |
|||
\tan \theta &= \frac{2t}{1-t^2}. |
|||
\end{align}</math> |
|||
Together with |
|||
:<math>d\theta = \frac{2}{1+t^2} \, dt,</math> |
|||
Rumus tersebut adalah [[substitusi setengah sudut tangen]], yang memungkinkan pengurangan komputasi [[integral]] s dan [[antiturunan]] fungsi trigonometri menjadi pecahan rasional. |
|||
===Turunan dan |
===Turunan dan integral dari fungsi trigonometri=== |
||
{| class="wikitable" style = "float:right; margin-left:1em; text-align:center; font-size:90%" |
|||
[[Turunan]] fungsi trigonometri dihasilkan dari fungsi sinus dan kosinus dengan menerapkan [[aturan hasil bagi]]. Nilai yang diberikan untuk [[antiderivatif]] dalam tabel berikut dapat diverifikasi dengan membedakannya. Angka pada {{mvar|C}} adalah [[konstanta integrasi]]. |
|||
!<math>f(x)</math> !! <math>f'(x)</math> !! <math display="inline">\int f(x) \, dx</math> |
|||
|- |
|||
|<math>\sin x</math>||<math>\cos x</math>||<math>-\cos x + C</math> |
|||
|- |
|||
|<math>\cos x</math>||<math>-\sin x</math>||<math>\sin x + C</math> |
|||
|- |
|||
|<math>\tan x</math>||<math>\sec^2 x = 1 + \tan^2 x</math>||<math>-\ln \left| \cos x \right| + C</math> |
|||
|- |
|||
|<math>\csc x</math>||<math>-\csc x \cot x</math>||<math>-\ln \left| \csc x + \cot x \right| + C</math> |
|||
|- |
|||
|<math>\sec x</math>||<math>\sec x \tan x</math>||<math>\ln \left| \sec x + \tan x \right| + C</math> |
|||
|- |
|||
|<math>\cot x</math>||<math>-\csc^2 x = - 1 - \cot^2 x</math>||<math>\ln \left| \sin x \right| + C</math> |
|||
|} |
|||
[[Turunan]] dari fungsi trigonometri dihasilkan dari fungsi sinus dan kosinus dengan menerapkan [[kaidah hasil-bagi]]. Pada tabel berikut, terdapat [[antiturunan]] dari fungsi trigonometri yang dapat dibenarkan dengan mendiferensialkannya. Catatan bahwa {{mvar|C}} merupakan [[konstanta integrasi]]. |
|||
Di sisi lain, turunan dari 'ko-fungsi' dapat diperoleh dengan menggunakan identitas trigonometri serta aturan rantai: |
|||
:<math> |
|||
\begin{array}{|c|c|c|}\hline |
|||
f(x) & |
|||
f'(x) & |
|||
\int f(x)\,dx \\ |
|||
\hline |
|||
\sin x & |
|||
\cos x & |
|||
-\cos x + C \\ |
|||
\cos x & |
|||
-\sin x & |
|||
\sin x + C \\ |
|||
\tan x & |
|||
\sec^2 x = 1+\tan^2 x & |
|||
-\ln \left( |\cos x|\right ) + C \\ |
|||
\cot x & |
|||
-\csc^2 x = -(1+\cot^2 x) & |
|||
\ln \left (|\sin x|\right ) + C \\ |
|||
\sec x & |
|||
\sec x\tan x & |
|||
\ln \left (|\sec x + \tan x|\right ) + C \\ |
|||
\csc x & |
|||
-\csc x \cot x & |
|||
-\ln \left (|\csc x + \cot x|\right ) + C \\ |
|||
\hline |
|||
\end{array} |
|||
</math> |
|||
== Fungsi terbalik == |
|||
==Inverse functions== |
|||
{{Main|Fungsi trigonometri terbalik}} |
|||
<!--Fungsi trigonometri bersifat periodik, dan karenanya bukan [[fungsi injeksi|injeksi]], jadi tegaskan pada nilai yang tidak memiliki [[fungsi terbalik]]. Namun, pada setiap interval di mana fungsi trigonometri [[monotonik]], seseorang dapat mendefinisikan fungsi invers, dan ini mendefinisikan fungsi trigonometri terbalik sebagai [[fungsi multinilai]]. To define a true inverse function, one must restrict the domain to an interval where the function is monotonic, and is thus [[bijection|bijective]] from this interval to its image by the function. The common choice for this interval, called the set of [[principal value]]s, is given in the following table. As usual, the inverse trigonometric functions are denoted with the prefix "arc" before the name or its abbreviation of the function.--> |
|||
:<math> |
:<math> |
||
\begin{ |
\begin{align} |
||
\frac{d\cos x}{dx} &= \frac{d}{dx}\sin\left(\frac{\pi}{2}-x\right)=-\cos\left(\frac{\pi}{2}-x\right)=-\sin x \, , \\ |
|||
\hline |
|||
\frac{d\csc x}{dx} &= \frac{d}{dx}\sec\left(\frac{\pi}{2} - x\right) = -\sec\left(\frac{\pi}{2} - x\right)\tan\left(\frac{\pi}{2} - x\right) = -\csc x \cot x \, , \\ |
|||
\text{Fungsi} & \text{Definisi} & \text{Domain} &\text{Kumpulan nilai pokok} |
|||
\frac{d\cot x}{dx} &= \frac{d}{dx}\tan\left(\frac{\pi}{2} - x\right) = -\sec^2\left(\frac{\pi}{2} - x\right) = -\csc^2 x \, . |
|||
\\ |
|||
\end{align} |
|||
\hline |
|||
y = \arcsin x & \sin y = x & -1 \le x \le 1 & -\frac{\pi}{2} \le y \le \frac{\pi}{2} \\ |
|||
y = \arccos x & \cos y = x & -1 \le x \le 1 & 0 \le y \le \pi \\ |
|||
y = \arctan x & \tan y = x & -\infty \le x \le \infty & -\frac{\pi}{2} < y < \frac{\pi}{2} \\ |
|||
y = \arccot x & \cot y = x & -\infty \le x \le \infty & 0 < y < \pi \\ |
|||
y = \arcsec x & \sec y = x & x<-1 \text{ or } x>1 & 0 \le y \le \pi,\; y \ne \frac{\pi}{2} \\ |
|||
y = \arccsc x & \csc y = x & x<-1 \text{ or } x>1 & -\frac{\pi}{2} \le y \le \frac{\pi}{2},\; y \ne 0 |
|||
\\\hline |
|||
\end{array} |
|||
</math> |
</math> |
||
==Fungsi invers== |
|||
<!--The notations sin<sup>−1,</sup> cos<sup>−1,</sup> etc. are often used for arcsin and arccos, etc. When this notation is used, inverse functions could be confused with multiplicative inverses. The notation with the "arc" prefix avoids such a confusion, though "arcsec" for arcsecant can be confused with "[[arcsecond]]". |
|||
{{Main|Fungsi trigonometri invers}} |
|||
{| class="wikitable" style = "float:right; margin-left:1em; text-align:center; font-size:90%" |
|||
! Fungsi !! Definisi<br>fungsi !! Domain<br>fungsi !! Himpunan dari nilai prinsip |
|||
|- |
|||
| <math>y = \arcsin x</math> || <math>\sin y = x</math> || <math>-1 \le x \le 1</math> || <math display="inline">-\frac{\pi}{2} \le y \le \frac{\pi}{2}</math> |
|||
|- |
|||
| <math>y = \arccos x</math> || <math>\cos y = x</math> || <math>-1 \le x \le 1</math> || <math display="inline">0 \le y \le \pi</math> |
|||
|- |
|||
| <math>y = \arctan x</math> || <math>\tan y = x</math> || <math>-\infty < x < \infty</math> || <math display="inline">-\frac{\pi}{2} < y < \frac{\pi}{2}</math> |
|||
|- |
|||
| <math>y = \arccot x</math> || <math>\cot y = x</math> || <math>-\infty < x < \infty</math> || <math display="inline">0 < y < \pi</math> |
|||
|- |
|||
| <math>y = \arcsec x</math> || <math>\sec y = x</math> || <math>x<-1 \text{ atau } x>1</math> || <math display="inline">0 \le y \le \pi,\; y \ne \frac{\pi}{2}</math> |
|||
|- |
|||
| <math>y = \arccsc x</math> || <math>\csc y = x</math> || <math>x<-1 \text{ atau } x>1</math> || <math display="inline">-\frac{\pi}{2} \le y \le \frac{\pi}{2},\; y \ne 0</math> |
|||
|}Fungsi trigonometri merupakan fungsi periodik, karena itu fungsi trigonometri bukanlah [[fungsi injektif|injektif]]. Lebih tepatnya, fungdi trigonometri tidak mempunyai [[Fungsi invers|kebalikannya]]. Akan tetapi, karena adanya [[fungsi monotonik|kemonotonan]] pada masing-masing interval dari fungsi trigonometri, maka dapat didefinisikan sebagai fungsi invers, dan ini mendefinisikan fungsi invers trigonometri sebagai [[fungsi bernilai banyak]]. Fungsi ini dapat didefinisikan dengan membatasi domain ulang ke interval saat fungsi adalah monotonik, dan [[fungsi bijeksi|bijektif]] dari interval tersebut ke citra fungsi. Interval umum yang dipilih di tabel disebut himpunan dari [[nilai prinsip]]. |
|||
Notasi dari fungsi invers trigonometri seringkali dilambangkan sebagai perpangkatan dari −1, sebagai contoh: {{math|sin<sup>−1</sup>}}, {{math|cos<sup>−1</sup>}}, dst. Namun perpangkatan tersebut dapat mengartikan invers perkalian. Jadi, untuk mencegah terjadinya keambiguan, notasi tersebut digantikan dengan prefiks "arc-", sebagai contoh: {{math|arcsin}},{{math|arccos}}, dst. |
|||
Just like the sine and cosine, the inverse trigonometric functions can also be expressed in terms of infinite series. They can also be expressed in terms of [[complex logarithm]]s. See [[Inverse trigonometric functions]] for details.--> |
|||
Mirip dengan fungsi sinus dan kosinus, fungsi invers trigonometri juga dapat dinyatakan dalam bentuk deret takhingga dan [[logaritma kompleks]]. |
|||
== Aplikasi == |
|||
== Sejarah == |
|||
== Etimologi == |
|||
== Lihat juga == |
|||
== Catatan == |
|||
== Referensi == |
|||
{{Reflist}} |
|||
== |
==Penerapan== |
||
{{Main|Penerapan dalam trigonometri}} |
|||
Tabel tabel dalam fungsi trigonometrik |
|||
===Sudut dan sisi segitiga=== |
|||
{{Trigonometri}} |
|||
Penerapan trigonometri ini dapat dipakai dalam hukum-hukum berikut. |
|||
{{math-stub}} |
|||
* [[Hukum sinus]], hukum yang menjelaskan perbandingan sisi dan sudut-sudut yang berhadapan dengan sisi pada segitiga sembarang. Hukum sinus dapat dibuktikan dengan membagi segitiga menjadi dua segitiga siku-siku dan menggunakan definisi dari fungsi sinus. Hukum sinus berguna dalam menghitung panjang dari sisi segitiga yang tidak diketahui jika ada dua sudut dan sisi yang diketahui. Hal ini muncul dalam sebuah teknik bernama ''[[triangulasi]]'', teknik yang menentukan jarak yang tidak diketahui dengan mengukur dua sudut dan jarak yang diperoleh. |
|||
* [[Hukum kosinus]], hukum yang mengaitkan panjang sisi-sisi segitiga dengan kosinus sudut pada segitiga sembarang. Hukum ini dapat dibuktikan dengan membagi segitiga menjadi dua segitiga siku-siku dan menggunakan [[teorema Pythagoras]]. Hukum ini dipakai untuk mencari panjang sisi ketiga dari segitiga jika hanya diketahui panjang dua sisi dan besar sudut yang diapit dua sisi tersebut, dan juga untuk menentukan besar sudut pada segitiga jika semua panjang sisinya diketahui. |
|||
* [[Hukum tangen]], hukum yang mengaitkan fungsi tangen dari dua sudut segitiga dan panjang dari sudut yang berhadapan. Mirip dengan hukum sinus, hukum ini dapat dipakai pada setiap kasus untuk dua sisi dan sudut yag diketahui, atau dua sudut dan satu sisi yang diketahui. |
|||
* [[Hukum kotangen]], hukum yang mempunyai kaitan antara panjang sisi segitiga dengan kotangen dari setengah sudut. Hukum ini dipakai untuk membuktikan rumus-rumus lain, seperti [[rumus Heron]], [[rumus pertama Mollweide]], dan [[rumus kedua Mollweide]]. |
|||
===Fungsi periodik=== |
|||
[[File:Synthesis square.gif|thumb|340px|right|Sebuah animasi yang memperlihatkan besarnya jumlah harmonik pada [[sintetis aditif]] dari [[gelombang persegi]].]] |
|||
Fungsi-fungsi trigonometri juga penting dalam ilmu fisika. Sebagai contoh, fungsi sinus dan kosinus digunakan untuk menjelaskan [[gerak harmonis sederhana]] seperti gerakan suatu benda bermassa yang terikat pada sebuah pegas, dan gerak pendulum sederhana pada sudut yang kecil dan dengan benda bermassa yang terikat pada sebuah tali, yang keduanya merupakan pemodelan dari banyak fenomena alam. Fungsi sinus dan kosinus adalah proyeksi satu dimensi dari [[Gerak melingkar seragam|gerak melingkar yang seragam]]. Fungsi-fungsi trigonometri juga terbukti berguna dalam kajian [[fungsi periodik]] umum. Pola-pola bergelombang karakteristik dari fungsi periodik berguna dalam menggambarkan fenomena yang berulang seperti [[gelombang]] suara atau cahaya.<ref name="Farlow_1993"/> |
|||
{{clear}} |
|||
[[File:Sawtooth Fourier Animation.gif|thumb|280px|Fungsi basis sinusoidal pada animasi di bawah dapat membentuk gelombang geriji seperti animasi di atas saat menambahkan beberapa suku.]] |
|||
Fungsi periodik {{math|1=''f'' (''x'')}} umumnya dapat dinyatakan sebagai jumlah [[gelombang sinus]] atau gelombang kosinus dalam [[deret Fourier]].<ref name="Folland_1992"/> Dengan Melambangkan [[fungsi basis]] sinus atau kosinus sebagai {{mvar|φ<sub>k</sub>}}, maka ekspansi dari fungsi periodik {{math|1=''f'' (''t'')}} membentuk: |
|||
: <math> f(t) = \sum _{k=1}^\infty c_k \varphi_k(t). </math> |
|||
Sebagai contoh, fungsi dari [[gelombang persegi]] dapat ditulis sebagai [[deret Fourier]] |
|||
: <math> f_\text{persegi}(t) = \frac{4}{\pi} \sum_{k=1}^\infty {\sin \big( (2k-1)t \big) \over 2k-1}.</math> |
|||
Dalam animasi gelombang persegi, dapat diperlihatkan bahwa hanya beberapa suku sudah menghasilkan aproksimasi yang hampir baik. Pada gambar bawah memperlihatkan superposisi dari beberapa suku dalam ekspansi [[gelombang geriji]]. |
|||
{{clear}} |
|||
== Catatan dan referensi == |
|||
{{div col|colwidth=30em}} |
|||
=== Catatan kaki === |
|||
{{Notelist}} |
|||
===Catatan=== |
|||
{{reflist|refs= |
|||
<ref name="Larson_2013">{{cite book |title=Trigonometry |edition=9th |first1=Ron |last1=Larson |publisher=Cengage Learning |date=2013 |isbn=978-1-285-60718-4 |page=153 |url=https://books.google.com/books?id=zbgWAAAAQBAJ |url-status=live |archive-url=https://web.archive.org/web/20180215144848/https://books.google.com/books?id=zbgWAAAAQBAJ |archive-date=15 February 2018 }} [https://books.google.com/books?id=zbgWAAAAQBAJ&pg=PA153 Extract of page 153] {{webarchive|url=https://web.archive.org/web/20180215144848/https://books.google.com/books?id=zbgWAAAAQBAJ&pg=PA153 |date=15 February 2018 }}</ref> |
|||
<!--<ref name="Aigner_2000">{{cite book |author-last1=Aigner |author-first1=Martin |author1-link=Martin Aigner |author-last2=Ziegler |author-first2=Günter M. |author-link2=Günter Ziegler |title=Proofs from THE BOOK |publisher=[[Springer-Verlag]] |edition=Second |date=2000 |isbn=978-3-642-00855-9 |page=149 |url=https://www.springer.com/mathematics/book/978-3-642-00855-9 |url-status=live |archive-url=https://web.archive.org/web/20140308034453/http://www.springer.com/mathematics/book/978-3-642-00855-9 |archive-date=8 March 2014 }}</ref> |
|||
<ref name="Remmert_1991">{{cite book |title=Theory of complex functions |author-first1=Reinhold |author-last1=Remmert |publisher=Springer |date=1991 |isbn=978-0-387-97195-7 |page=327 |url=https://books.google.com/books?id=CC0dQxtYb6kC |url-status=live |archive-url=https://web.archive.org/web/20150320010718/http://books.google.com/books?id=CC0dQxtYb6kC |archive-date=20 March 2015 }} [https://books.google.com/books?id=CC0dQxtYb6kC&pg=PA327 Extract of page 327] {{webarchive|url=https://web.archive.org/web/20150320010448/http://books.google.com/books?id=CC0dQxtYb6kC&pg=PA327 |date=20 March 2015 }}</ref>--> |
|||
<ref name="Kannappan_2009">{{cite book |author-last=Kannappan |author-first=Palaniappan |title=Functional Equations and Inequalities with Applications |date=2009 |publisher=Springer |isbn=978-0387894911}}</ref> |
|||
<ref name="Farlow_1993">{{cite book |title=Partial differential equations for scientists and engineers |url=https://books.google.com/books?id=DLUYeSb49eAC&pg=PA82 |author-first=Stanley J. |author-last=Farlow|author-link= Stanley Farlow |page=82 |isbn=978-0-486-67620-3 |publisher=Courier Dover Publications |edition=Reprint of Wiley 1982 |date=1993 |url-status=live |archive-url=https://web.archive.org/web/20150320011420/http://books.google.com/books?id=DLUYeSb49eAC&pg=PA82 |archive-date=20 March 2015 }}</ref> |
|||
<ref name="Folland_1992">See for example, {{cite book |author-first=Gerald B. |author-last=Folland |title=Fourier Analysis and its Applications |publisher=American Mathematical Society |edition=Reprint of Wadsworth & Brooks/Cole 1992 |chapter-url=https://books.google.com/books?id=idAomhpwI8MC&pg=PA77 |pages=77ff |chapter=Convergence and completeness |date=2009 |isbn=978-0-8218-4790-9 |url-status=live |archive-url=https://web.archive.org/web/20150319230954/http://books.google.com/books?id=idAomhpwI8MC&pg=PA77 |archive-date=19 March 2015 }}</ref> |
|||
<!--<ref name="Boyer_1991">Boyer, Carl B. (1991). A History of Mathematics (Second ed.). John Wiley & Sons, Inc. {{isbn|0-471-54397-7}}, hlm. 210.</ref> |
|||
<ref name="Gingerich_1986">{{cite magazine |title=Islamic Astronomy |author-first=Owen |author-last=Gingerich |magazine=[[Scientific American]] |date=1986 |volume=254 |page=74 |url=http://faculty.kfupm.edu.sa/PHYS/alshukri/PHYS215/Islamic_astronomy.htm |access-date=13 July 2010 |archive-url=https://web.archive.org/web/20131019140821/http://faculty.kfupm.edu.sa/PHYS/alshukri/PHYS215/Islamic_astronomy.htm |archive-date=19 October 2013}}</ref> |
|||
<ref name="mact-biog">{{cite web |publisher=School of Mathematics and Statistics University of St Andrews, Scotland |title=Madhava of Sangamagrama |author-first1=J. J. |author-last1=O'Connor |author-first2=E. F. |author-last2=Robertson |url=http://www-gap.dcs.st-and.ac.uk/~history/Biographies/Madhava.html |archive-url=https://web.archive.org/web/20060514012903/http://www-gap.dcs.st-and.ac.uk/~history/Biographies/Madhava.html |url-status=dead |archive-date=14 May 2006 |access-date=8 September 2007 }}</ref> |
|||
<ref name="Fincke">{{cite web |url=http://www-history.mcs.st-andrews.ac.uk/Biographies/Fincke.html |title=Fincke biography |access-date=15 March 2017 |url-status=live |archive-url=https://web.archive.org/web/20170107035144/http://www-history.mcs.st-andrews.ac.uk/Biographies/Fincke.html |archive-date=7 January 2017 }}</ref> |
|||
<ref name="Bourbaki_1994">{{cite book |title=Elements of the History of Mathematics |url=https://archive.org/details/elementsofhistor0000bour |url-access=registration |author-first=Nicolás |author-last=Bourbaki |publisher=Springer |date=1994}}</ref> |
|||
<ref name="Gunter_1620">{{cite book |author-first=Edmund |author-last=Gunter |author-link=Edmund Gunter |title=Canon triangulorum |date=1620}}</ref> |
|||
<ref name="Roegel_2010">{{cite web |title=A reconstruction of Gunter's Canon triangulorum (1620) |editor-first=Denis |editor-last=Roegel |type=Research report |publisher=HAL |date=6 December 2010 |id=inria-00543938 |url=https://hal.inria.fr/inria-00543938/document |access-date=28 July 2017 |url-status=live |archive-url=https://web.archive.org/web/20170728192238/https://hal.inria.fr/inria-00543938/document |archive-date=28 July 2017}}</ref> |
|||
<ref name="Plofker_2009">See Plofker, ''[[Mathematics in India (book)|Mathematics in India]]'', Princeton University Press, 2009, hlm. 257<br>See {{cite web |url=http://www.clarku.edu/~djoyce/trig/ |title=Clark University |url-status=live |archive-url=https://web.archive.org/web/20080615133310/http://www.clarku.edu/~djoyce/trig/ |archive-date=15 June 2008 }}<br>See Maor (1998), chapter 3, regarding the etymology.</ref>--> |
|||
}} |
|||
===Referensi=== |
|||
{{refbegin}} |
|||
* {{AS ref}} |
|||
* [[Lars Ahlfors]], ''Complex Analysis: an introduction to the theory of analytic functions of one complex variable'', second edition, [[McGraw-Hill Book Company]], New York, 1966. |
|||
* [[Carl Benjamin Boyer|Boyer, Carl B.]], ''A History of Mathematics'', John Wiley & Sons, Inc., 2nd edition. (1991). {{isbn|0-471-54397-7}}. |
|||
* Gal, Shmuel and Bachelis, Boris. An accurate elementary mathematical library for the IEEE floating point standard, ACM Transactions on Mathematical Software (1991). |
|||
* Joseph, George G., ''The Crest of the Peacock: Non-European Roots of Mathematics'', 2nd ed. [[Penguin Books]], London. (2000). {{isbn|0-691-00659-8}}. |
|||
* Kantabutra, Vitit, "On hardware for computing exponential and trigonometric functions," ''IEEE Trans. Computers'' '''45''' (3), 328–339 (1996). |
|||
* Maor, Eli, ''[https://web.archive.org/web/20040404234808/http://www.pupress.princeton.edu/books/maor/ Trigonometric Delights]'', Princeton Univ. Press. (1998). Reprint edition (2002): {{isbn|0-691-09541-8}}. |
|||
* Needham, Tristan, [https://web.archive.org/web/20040602145226/http://www.usfca.edu/vca/PDF/vca-preface.pdf "Preface"]" to ''[http://www.usfca.edu/vca/ Visual Complex Analysis]''. Oxford University Press, (1999). {{isbn|0-19-853446-9}}. |
|||
* {{citation |last1=Nielsen |first1=Kaj L. |title=Logarithmic and Trigonometric Tables to Five Places |edition=2nd |location=New York|publisher=[[Barnes & Noble]] |date=1966 |lccn=61-9103}} |
|||
* O'Connor, J. J., and E. F. Robertson, [https://web.archive.org/web/20130120084848/http://www-gap.dcs.st-and.ac.uk/~history/HistTopics/Trigonometric_functions.html "Trigonometric functions"], ''[[MacTutor History of Mathematics archive]]''. (1996). |
|||
* O'Connor, J. J., and E. F. Robertson, [http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Madhava.html "Madhava of Sangamagramma"] {{Webarchive|url=https://web.archive.org/web/20060226001644/http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Madhava.html |date=2006-02-26 }}, ''[[MacTutor History of Mathematics archive]]''. (2000). |
|||
* Pearce, Ian G., [http://www-history.mcs.st-andrews.ac.uk/history/Projects/Pearce/Chapters/Ch9_3.html "Madhava of Sangamagramma"] {{Webarchive|url=https://web.archive.org/web/20060505201342/http://www-history.mcs.st-andrews.ac.uk/history/Projects/Pearce/Chapters/Ch9_3.html |date=2006-05-05 }}, ''[[MacTutor History of Mathematics archive]]''. (2002). |
|||
* {{ citation | last1 = Protter | first1 = Murray H. | last2 = Morrey | first2 = Charles B., Jr. | year = 1970 | lccn = 76087042 | title = College Calculus with Analytic Geometry | edition = 2nd | publisher = [[Addison-Wesley]] | location = Reading }} |
|||
* Weisstein, Eric W., [http://mathworld.wolfram.com/Tangent.html "Tangent"] {{Webarchive|url=https://web.archive.org/web/20060719202529/http://mathworld.wolfram.com/Tangent.html |date=2006-07-19 }} from ''[[MathWorld]]'', diakses pada tanggal 21 Januari 2006. |
|||
{{refend}} |
|||
{{div col end}} |
|||
[[Kategori:Trigonometri]] |
[[Kategori:Trigonometri]] |
||
[[Kategori:Sudut]] |
|||
[[Kategori:Fungsi trigonometri]] |
|||
[[Kategori:Fungsi analitik]] |
|||
Revisi terkini sejak 21 Maret 2024 00.42
| Trigonometri |
|---|
 |
| Rujukan |
| Aturan dan teorema |
| Kalkulus |

Dalam matematika, fungsi trigonometri merupakan fungsi real yang mengaitkan sudut dari segitiga bersiku dengan perbandingan antara dua sisi segitiga. Fungsi ini memiliki penerapan yang sangat luas dalam bidang sains terkait dengan geometri (misalnya navigasi, geodesi, mekanika benda langit, mekanika zat padat, dan cabang lainnya). Fungsi ini merupakan contoh fungsi periodik paling sederhana, dan juga memiliki penerapan yang sangat luas dalam mempelajari fenomena periodik melalui analisis Fourier.
Fungsi trigonometri seperti sinus, kosinus, dan tangen merupakan fungsi yang paling sering dipakai dalam matematika modern; sedangkan fungsi inversnya seperti kosekan, sekan, dan kotangen jarang dipakai. Masing-masing keenam fungsi tersebut mempunyai fungsi invers yang sama dan sejalan di antara fungsi hiperbolik.
Definisi fungsi trigonometri terlama, yang berkaitan dengan segitiga bersudutkan siku-siku, hanya mendefinisikannya untuk sudut lancip. Secara geometris, fungsi sinus dan kosinus seringkali dapat diperluas menjadi fungsi yang mempunyai domain yang mengandung seluruh garis bilangan real, maka domain fungsi lainnya adalah garis bilangan real dengan setiap titik terpencilnya hilang. Definisi modern yang mengekspresikan fungsi trigonometri sebagai deret takhingga atau sebagai penyelesai dari persamaan diferensial, memungkinkan perluasan domain dari fungsi sinus dan kosinus menjadi domain yang mengandung seluruh bidang kompleks, dan domain dari fungsi trigonometri lain menjadi domain mengandung bidang kompleks dengan setiap titik terpencilnya hilang.
Notasi
[sunting | sunting sumber]Fungsi trigonometri biasanya menyingkatkan namanya menggunakan tiga huruf, contohnya: sinus disingkat "sin", kosinus "cos", tangen disingkat "tan", sekan disingkat "sec", kosekan disingkat "csc",[a] dan kotangen disingkat "cot". Terlebih lagi, fungsi trigonometri juga menggunakan notasi fungsional, misalnya sin(x). Tanda kurung wajib digunakan karena dapat menimbulkan kebingungan. Sebagai contohnya seperti fungsi dapat dipandang sebagai atau juga dapat dipandang sebagai .
Tidak seperti notasi fungsi lainnya, bilangan bulat positif yang muncul sebagai superskrip setelah simbol fungsi, bukan dinyatakan sebagai perpangkatan terhadap komposisi fungsi, melainkan dinyatakan sebagai perkalian teriterasi. Sebagai contoh, dan berarti , bukan .
Eksponen biasanya dipakai untuk menyatakan fungsi invers, bukan invers perkalian. Sebagai contoh, dan menyatakan fungsi invers trigonometri, dan notasi tersebut dapat ditulis pula sebagai . Persamaan menyiratkan , bukan . Pada kasus tersebut, superskrip dapat dipandang untuk menyatakan fungsi yang berulang, tetapi superskrip yang bernilai negatif selain jarang dipakai.
Definisi segitiga bersiku
[sunting | sunting sumber]

Jika sudut lancip dinyatakan sebagai θ, maka setiap sudut siku-siku yang mempunyai sudut θ dikatakan sebangun terhadap satu sama lain; dalam artian, perbandingan dari setiap dua panjang sisinya hanya bergantung pada θ. Jadi, keenam perbandingan tersebut mendefinisikan enam fungsi trigonometri dari θ. Definisi berikut mengatakan bahwa hipotenusa (sisi miring) merupakan panjang dari sisi yang berhadapan dengan sudut siku-siku, sisi depan merupakan panjang sisi yang berhadap dari sudut θ, dan sisi samping merupakan panjang sisi yang berhadapan dengan sudut θ dan sudut siku-siku.[1][2]
|
|
|
|
|
|
Dalam segitiga siku-siku, jumlah dari dua sudut lancip sama dengan sudut siku-siku, yaitu 90° atau π2 radian. Karena itu, dan mewakili perbandingan yang sama sehingga menjadi sama. Identitas dan kaitan antara fungsi trigonometri lainnya yang sejalan diringkas dalam tabel berikut.
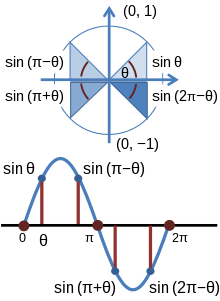
Gambar bawah: Perbandingan grafik fungsi dengan sudut sinus. Sudut-sudut dari panel di atas diidentifikasi
| Fungsi | Penjelasan | Kaitan | |
|---|---|---|---|
| dalam bentuk radian | dalam bentuk derajat | ||
| sinus | depanmiring | ||
| kosinus | sampingmiring | ||
| tangen | depansamping | ||
| kotangen | sampingmiring | ||
| sekan | miringsamping | ||
| kosekan | miringdepan | ||
Perbandingan radian dengan derajat
[sunting | sunting sumber]Dalam penerapan geometri, argumen fungsi trigonometri umumnya merupakan ukuran sudut. Setiap sudut biasanya diukur dan satuan konvensional berupa derajat. Sebagai contoh, sudut siku-siku ditulis 90° dan putaran penuh ditulis 360°.[b]
Namun dalam kalkulus dan analisis matematika, fungsi trigonometri umumnya dipandang lebih abstrak sebagai fungsi real ataupun kompleks, bukan sudut. Bahkan fungsi sepeti sin dan cos dapat didefinisikan untuk semua bilangan kompleks dalam bentuk fungsi eksponensial melalui deret pangkat,[4] atau dapat didefinisikan sebagai penyelesaian nilai awal khusus terhadap persamaan diferensial (lihat dibawah).[5] Definisi tersebut tidak mengacu pada gagasan dalam geometri. Adapun empat fungsi lainnya seperti tan, cot, sec, dan csc dapat didefinisikan sebagia hasil-bagi dan timbal balik dari sin dan cos, kecuali ketika nol muncul di penyebut. Untuk argumen real, hal ini dapat dibuktikan bahwa definisi tersebut sesuai dengan definisi geometri elementer jika argumennya dipandang sebagai sudut yang dinyatakan dalam bentuk radian.[4] Lebih lanjut, definisi tersebut memberikan hasil dalam bentuk yang sederhana untuk turunan dan integral taktentu dari fungsi trigonometri.[6] Jadi dalam cabang selain geometri elementer, radian dipandang sebagai satuan alami dalam matematika untuk menjelaskan ukuran setiap sudut.
Ketika satuan yang dipakai adalah radian, maka sudut dinyatakan sebagai panjang busur dari lingkaran satuan yang berhadapan dengannya. Sebagai contoh, sudut yang berhadapan dengan busur dengan panjang 1 di lingkaran satuan adalah 1 rad (≈ 57,3°), dan putaran penuh (360°) sama dengan 2π (≈ 6,28) rad. Untuk bilangan real x, notasi sin x, cos x, dst. mengacu pada nilai dari fungsi trigonometri yang dihitung pada sudut x rad. Jika satuan yang dimaksud adalah derajat, maka tanda derajat harus diperlihatkan secara eksplisit (sebagai contoh, sin x°, cos x°, dsb.). Dengan menggunakan notasi yang standar, argumen dari x untuk fungsi trigonometri memenuhi kaitan dari rumus
sehingga, sebagai contoh, sin π = sin 180° ketika x = π. Dalam cara ini, simbol derajat dapat dipandang sebagai sebuah konstanta matematika, sehingga 1° = π180 ≈ 0,0175.
Definisi fungsi trigonometri melalui lingkaran satuan
[sunting | sunting sumber]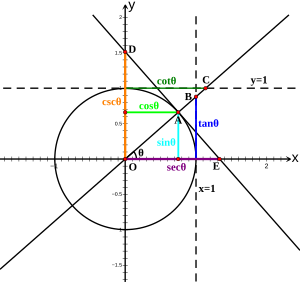
Enam fungsi trigonometri dapat didefinisikan sebagai nilai dari titik koordinat di bidang Euklides yang berkaitan dengan sebuah lingkaran berjari-jari satu yang berpusat di titik asal O dari koordinat sistem, yaitu lingkaran satuan. Sedangkan definisi segitiga bersiku yang memungkinkan definisi fungsi trigonometri untuk sudut di antara 0 dan radian (90°), maka definisi lingkaran satuan memungkinkan bahwa domain dari fungsi trigonometri diperluas untuk semua bilangan real positif dan negatif.
Misalkan adalah sinar yang didapatkan dengan memutarnya setengah sudut positif θ dari sumbu-x (putarannya berlawanan arah jarum jam untuk dan searah jarum jam untuk ). Sinar ini memotong lingkaran satuan di titik Sinar jika perlu diperpanjang garisnya, memotong garis persamaan di titik dan garis persamaan di titik Garis yang menyinggung lingkaran satuan di titik A dikatakan tegaklurus terhadap serta memotong sumbu-y di titik dan sumbu-x di titik Koordinat dari titik tersebut yang memberikan nilai dari semua fungsi trigonometri untuk setiap nilai real sebarang θ, dapat dicari sebagai berikut.
Fungsi trigonometri cos didefinisikan sebagai nilai koordinat-x dari titik A, sedangkan fungsi trigonometri sin didefinisikan sebagai nilai koordinat-y dari titik A.
- and [7]
Dengan kisaran (bahasa Inggris: range) , maka definisi ini bertepatan dengan definisi segitiga sudut siku-siku dengan mengambil segitiga siku-siku agar mempunyai jari-jari lingkaran satuan OA sebagai hipotenusa. Karena persamaan berlaku untuk semua titik pada lingkran satuan, maka definisi kosinus dan sinus ini juga memenuhi identitas Pythagoras.
Selain kedua fungsi trigonometri di atas, fungsi lainnya dapat ditemukan di sepanjang lingkaran satuan
- dan
- dan
Dengan menerapkan identitas Pythagoras dan metode bukti geometri, maka dapat diperlihatkan bahwa definisi ini bertepatan dengan definisi fungsi tangen, kotangen, sekan dan kosekan dalam bentuk fungsi sinus dan kosinus. Dengan kata lain,

Karena putaran sudut dari tidak mengubah posisi atau ukuran bentuk, titik-titik A, B, C, D, dan E adalah sama untuk dua sudut yang mempunyai selisihnya yang berupakan kelipatan bilangan bulat dari . Jadi, fungsi trigonometri merupakan fungsi berkala dengan periode . Artinya, persamaan
- dan
berlaku untuk setiap sudut θ dan setiap bilangan bulat k. Hal ini berlaku benar untuk keempat fungsi trigonometri lainnya. Dengan mengamati tanda dan kemonotonan dari fungsi sinus, kosekan, kotangen, dan sekan dalam yang ada di dalam keempat kuadran, maka untuk fungsi-fungsi yang dikatakan periodik dapat diperlihatkan bahwa merupakan nilai yang paling terkecil (dengan kata lain, merupakan periode dasar dari fungsi tersebut). Namun, saat putaran sudut , titik B dan C telah kembali ke posisi awal sehingga fungsi tangen dan fungsi kotangen mempunyai periode dasar dari . Dengan kata lain, persamaan
- dan
berlaku untuk setiap sudut θ dan setiap bilangan bulat k.
Nilai aljabar
[sunting | sunting sumber]
Bentuk aljabar yang berupakan sudut yang sangat penting dinyatakan sebagai berikut:
Dengan menulis pembilang sebagai akar kuadrat dari bilangan bulat taknegatif berurutan serta penyebutnya adalah 2, maka cara ini dengan mudah mengingat nilai-nilai fungsi trigonometri.[8]
Namun, bentuk aljabar yang sederhana biasanya tidak ada untuk sudut lainnya yang merupakan kelipatan rasional sudut siku-siku.
- Untuk sudut yang diukur dalam satuan derajat merupakan kelipatan dari tiga, nilai trigonometri eksak dari fungsi sinus dan kosinus dapat dinyatakan dalam bentuk akar kuadrat. Jadi, nilai tersebut dapat dikonstruksi dengan menggunakan penggaris dan jangka.
- Untuk sudut berupa bilangan bulat dalam satuan derajat, nilai dari fungsi sinus dan kosinus dapat dinyatakan dalam bentuk akar kuadrat dan akar kubik dari bilangan kompleks takreal. Teori Galois membuktikan bahwa jika sudut bukan kelipatan dari 3°, maka akar kubik dari bilangan takreal tidak dapat dihindari.
- Untuk sudut yang dinyatakan dalam satuan derajat adalah bilangan rasional, nilai fungsi sinus dan kosinus merupakan bilangan aljabar yang dapat dinyatakan dalam bentuk akar ke-n. Hasil ini berasal dari suatu pernyataan yang mengatakan bahwa grup Galois dari polinomial siklotomik dikatakan siklik.
- Untuk sudut yang dinyatakan dalam satuan derajat bukanlah bilangan rasional, maka nilai sudut dari fungsi sinus maupun kosinus merupakan bilangan transendental. Pernyataan ini merupakan korolari dari teorema Baker yang dibuktikan pada tahun 1966.
Nilai aljabar sederhana
[sunting | sunting sumber]Berikut ada sebuah tabel yang memuat kumpulan-kumpulan nilai fungsi sinus, kosinus, dan tangen yang merupakan kelipatan dari 15 derajat, dimulai dari 0 derajat sampai dengan 90 derajat.
| θ dalam satuan radian | θ dalam satuan derajat | |||
|---|---|---|---|---|
| takterdefinisikan |
Dalam kalkulus
[sunting | sunting sumber]



Fungsi trigonometri dikatakan terdiferensialkan dan analitik di setiap titik yang didefinisikannya. Artinya, titik-titik tersebut ada dimana-mana untuk fungsi trigonometri seperti sinus, kosinus. Titik-titik tersebut ada dimana-mana di fungsi tangen, kecuali di π/2 + kπ untuk setiap bilangan bulat k.
Fungsi trignometri merupakan fungsi berkala, dan periode primitifnya bernilai 2π untuk fungsi sinus dan kosinus, dan π untuk fungsi tangen, yang naik di masing-masing selang terbuka (π/2 + kπ, π/2 + (k + 1)π). Pada masing-masing titik akhir selang tersebut, fungsi tangen mempunyai asimtot yang mengarah vertikal.
Dalam kalkulus, fungsi trigonometri dapat didefinisikan dengan menggunakan deret kuasa ataupun persamaan diferensial. Namun, menggunakan persamaan diferensial terasa lebih alami saat mendefinisikan fungsi trigonometri, karena, sebagai contoh, pemilihan koefisien dari deret kuasa dapat muncul sebagai bilangan yang cukup sebarang, dan persamaan diferensial juga cukup mudah menyimpulkan identitas Pythagoras.
Definisi dengan menggunakan persamaan diferensial
[sunting | sunting sumber]Fungsi sinus dan kosinus dapat didefinisikan sebagai penyelesaian tunggal untuk masalah nilai awal:
Dengan menurunkannya lagi, maka diperoleh dan . Jadi, fungsi sinus dan kosinus merupakan penyelesaian untuk persamaan diferensial biasa
Fungsi tangen dapat diturunkan dengan menerapkan aturan hasil bagi dari, maka
Perluasan deret pangkat
[sunting | sunting sumber]Dengan menerapkan persamaan diferensial untuk deret pangkat dengan koefisien yang belum ditentukan, maka fungsi sinus dan kosinus dapat disimpulkan sebagai relasi rekurensi mengenai koefisien deret Taylor dari kedua fungsi tersebut. Relasi rekurensinya dapat diselesaikan dengan mudah serta memberikan perluasan deret[9]
Ruji kekonvergenan dari deret tersebut adalah takhingga. Jadi, fungsi sinus dan kosinus dapat diperluas menjadi fungsi menyeluruh, atau fungsi ini disebut "sinus" dan "kosinus"), karena (berdasarkan definisi) fungsi tersebut merupakan fungsi bernilai kompleks yang terdefinisi dan holomorfik di seluruh bidang kompleks.
Ketika kedua fungsi tersebut didefinisikan sebagai pecahan dari fungsi menyeluruh, fungsi trigonometri lainnya dapat diperluas menjadi fungsi meromorfik. Hal ini mengartikan bahwa fungsi adalah holomorfik di seluruh bidang kompleks, kecuali ada setiap titik terpencil yang disebut kutub. Disini, kutubnya merupakan bilangan-bilangan dari bentuk untuk fungsi tangen dan fungsi sekan, atau untuk fungsi kotangen dan fungsi kosekan, dengan k adalah bilangan bulat sebarang.
Relasi rekurensi juga dapat dihitung untuk koefisien deret Taylor dari fungsi trigonometri lain. Deret-deret ini mempunyai ruji kekonvergenan terhingga. Koefisiennya mempunyai pandangan kombinatorial, yang mengatakan bahwa koefisiennya menghitung permutasi selang-seling dari himpunan hingga.[10] Lebih tepatnya, dengan mendefinisikan Un adalah bilangan atas/bawah ke-n, Bn adalah bilangan Bernoulli ke-n, dan En adalah bilangan Euler ke-n, maka ada empat perluasan deret berikut didapatkan.[11]
Perluasan pecahan berlanjut
[sunting | sunting sumber]Perluasan pecahan berlanjut berikut valid di seluruh bidang kompleks:
Pecahan yang terakhir dipakai pertama kali menurut sejarah dalam bukti bahwa π irasional.[12]
Perluasan darab takhingga
[sunting | sunting sumber]Darab takhingga untuk fungsi sinus sangat penting dalam analisis kompleks, yang dinyatakan sebagai:
Bukti perluasan darab ini dapat dilihat disini. Melalui rumus ini, dapat disimpulkan bahwa
Kaitan dengan rumus Euler
[sunting | sunting sumber]
Rumus Euler mengaitkan fungsi sinus dan kosinus dengan fungsi eksponensial:
Rumus ini biasanya dipandang untuk bilangan real x, tetapi tetap benar untuk semua bilangan kompleks. Rumus ini dapat dibuktikan sebagai berikut: Misalkan dan . Karena untuk j = 1, 2, maka menurut kaidah hasil bagi, . Jadi, adalah fungsi konstan, yang sama dengan 1, ketika Hal ini membuktikan rumus tersebut.
Selanjutnya, didapatkan persamaan dan . Dengan menyelesaikan sistem linear pada fungsi sinus dan kosinus, maka dapat dinyatakan dalam bentuk fungsi eksponensial:
Ketika x adalah bilangan real, kedua fungsi tersebut dapat ditulis ulang sebagai
Hampir identitas trigonometri dapat dibuktikan dengan memnyatakan fungsi trigonometri dalam bentuk fungsi eksponensial kompleks melalui rumus di atas, dan kemudian menggunakan identitas untuk menyederhanakan hasilnya.
Definisi yang menggunakan persamaan fungsional
[sunting | sunting sumber]Fungsi trigonometri juga dapat didefinisikan dengan menggunakan berbagai persamaan fungsional. Sebagai contoh,[13] fungsi sinus dan kosinus membentuk pasangan tunggal dari fungsi kontinu yang memenuhi rumus selisih.
dan ditambah dengan syarat
Dalam bidang kompleks
[sunting | sunting sumber]Fungsi sinus dan kosinus dari bilangan kompleks dapat dinyatakan dalam bentuk fungsi sinus, kosinus, dan hiperbolik sebagai berikut:
Grafik fungsi trigonometri sebagai fungsi bernilai kompleks dapat digambarkan dengan memanfaatkan pewarnaan domain. Berbagai tampilan fungsi yang unik hingga fungsi kompleks dapat dilhat dari grafik; contohnya dapat dilihat bahwa fungsi sinus dan kosinus menjadi tidak terbatas ketika bagian imajiner semakin besar (dengan warna putih menyatakan takhingga), dan fungsi yang memuat pole sederhana rupanya merupakan warna yang berputar di sekitar nol atau kutub sekali. Grafik-grafik di bawah yang dibandingkan dengan fungsi hiperbolik yang berpadanan memperlihatkan kaitan antara kedua fungsi tersebut.

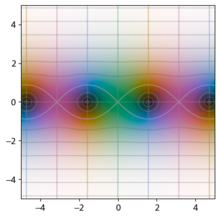
|
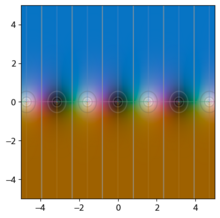
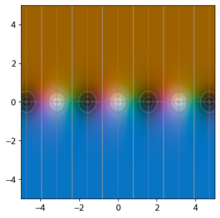
|


|
Identitas dasar
[sunting | sunting sumber]Ada banyak identitas yang saling berhubungan dengan fungsi trigonometri. Bagian ini memuat identitas yang paling dasar; identitas yang lebih banyak dapat lihat di Daftar identitas trigonometri. Identitas berikut dapat dibuktikan secara geometri mellaui definisi lingkaran satuan atau definisi bersudut siku-siku (walauapun definisi terakhir harus mengambil sudut yang bukan berada di dalam interval [0, π/2], lihat Bukti identitas trigonometri). Bukti tanpa geometri, yakni hanya dengan menggunakan alat kalkulus, dapat dipakai menggunakan persamaan diferensial langsung, melalui cara yang mirip dengan bukti sebelumnya. Selain itu, buktinya dapat menggunakan identitas Euler pula untuk menyatakan semua fungsi trigonometri dalam benetuk eksponensial kompleks beserta menggunakan sifat-sifat fungsi eksponensial.
Paritas
[sunting | sunting sumber]Fungsi kosinus dan sekan merupakan fungsi genap, sedangkan fungsi trigonometri lain merupakan fungsi ganjil. Paritas dari fungsi-fungsi ini ditulis sebagai berikut:
Periode
[sunting | sunting sumber]Semua fungsi trigonometri merupakan fungsi periode. Fungsi-fungsi tersebut mempunyai periode yang paling terkecil 2π, kecuali untuk fungsi tangen dan kotangen yang mempunyai π sebagai periode yang paling terkecil. Hal ini mengartikan bahwa untuk setiap bilangan bulat k, maka diperoleh:
Identitas Pythagoras
[sunting | sunting sumber]Identitas Pythagoras merupakan ekspresi teorema Pythagoras yang berupa fungsi trigonometri. Identitasnya adalah
Rumus jumlah dan selisih
[sunting | sunting sumber]Rumus jumlah dan selisih dapat memperluas fungsi sinus, kosinus, dan tangen dari jumlah atau selisih dari dua sudut yang dipandang sebagai fungsi sinus dan kosinus dan tangen dari sudut tersendiri. Rumus-rumus ini dapat diturunkan melalui geometri, berdasarkan argumen Ptolemaus. Selain itu, rumus ini juga dapat diturunkan secara aljabar menggunakan rumus Euler.
- Penjumlahan
- Selisih
Ketika dua sudut adalah sama, maka rumus penjumlahan mereduksi ke persamaan yang lebih sederhana, yang dikenal sebagai rumus rangkap dua.
Identitas tersebut dapat dipakai untuk menurunkan identitas darab-ke-jumlah.
Dengan memisalkan , maka semua fungsi trigonometri dari dapat dinyatakan sebagai pecahan rasional dari :
Fungsi yang terakhir merupakan substitusi setengah sudut tangen, yang dipakai untuk membantu perhitungan integral dari fungsi trigonometri lain menjadi fungsi rasional tersebut.
Turunan dan integral dari fungsi trigonometri
[sunting | sunting sumber]Turunan dari fungsi trigonometri dihasilkan dari fungsi sinus dan kosinus dengan menerapkan kaidah hasil-bagi. Pada tabel berikut, terdapat antiturunan dari fungsi trigonometri yang dapat dibenarkan dengan mendiferensialkannya. Catatan bahwa C merupakan konstanta integrasi.
Di sisi lain, turunan dari 'ko-fungsi' dapat diperoleh dengan menggunakan identitas trigonometri serta aturan rantai:
Fungsi invers
[sunting | sunting sumber]| Fungsi | Definisi fungsi |
Domain fungsi |
Himpunan dari nilai prinsip |
|---|---|---|---|
Fungsi trigonometri merupakan fungsi periodik, karena itu fungsi trigonometri bukanlah injektif. Lebih tepatnya, fungdi trigonometri tidak mempunyai kebalikannya. Akan tetapi, karena adanya kemonotonan pada masing-masing interval dari fungsi trigonometri, maka dapat didefinisikan sebagai fungsi invers, dan ini mendefinisikan fungsi invers trigonometri sebagai fungsi bernilai banyak. Fungsi ini dapat didefinisikan dengan membatasi domain ulang ke interval saat fungsi adalah monotonik, dan bijektif dari interval tersebut ke citra fungsi. Interval umum yang dipilih di tabel disebut himpunan dari nilai prinsip.
Notasi dari fungsi invers trigonometri seringkali dilambangkan sebagai perpangkatan dari −1, sebagai contoh: sin−1, cos−1, dst. Namun perpangkatan tersebut dapat mengartikan invers perkalian. Jadi, untuk mencegah terjadinya keambiguan, notasi tersebut digantikan dengan prefiks "arc-", sebagai contoh: arcsin,arccos, dst.
Mirip dengan fungsi sinus dan kosinus, fungsi invers trigonometri juga dapat dinyatakan dalam bentuk deret takhingga dan logaritma kompleks.
Penerapan
[sunting | sunting sumber]Sudut dan sisi segitiga
[sunting | sunting sumber]Penerapan trigonometri ini dapat dipakai dalam hukum-hukum berikut.
- Hukum sinus, hukum yang menjelaskan perbandingan sisi dan sudut-sudut yang berhadapan dengan sisi pada segitiga sembarang. Hukum sinus dapat dibuktikan dengan membagi segitiga menjadi dua segitiga siku-siku dan menggunakan definisi dari fungsi sinus. Hukum sinus berguna dalam menghitung panjang dari sisi segitiga yang tidak diketahui jika ada dua sudut dan sisi yang diketahui. Hal ini muncul dalam sebuah teknik bernama triangulasi, teknik yang menentukan jarak yang tidak diketahui dengan mengukur dua sudut dan jarak yang diperoleh.
- Hukum kosinus, hukum yang mengaitkan panjang sisi-sisi segitiga dengan kosinus sudut pada segitiga sembarang. Hukum ini dapat dibuktikan dengan membagi segitiga menjadi dua segitiga siku-siku dan menggunakan teorema Pythagoras. Hukum ini dipakai untuk mencari panjang sisi ketiga dari segitiga jika hanya diketahui panjang dua sisi dan besar sudut yang diapit dua sisi tersebut, dan juga untuk menentukan besar sudut pada segitiga jika semua panjang sisinya diketahui.
- Hukum tangen, hukum yang mengaitkan fungsi tangen dari dua sudut segitiga dan panjang dari sudut yang berhadapan. Mirip dengan hukum sinus, hukum ini dapat dipakai pada setiap kasus untuk dua sisi dan sudut yag diketahui, atau dua sudut dan satu sisi yang diketahui.
- Hukum kotangen, hukum yang mempunyai kaitan antara panjang sisi segitiga dengan kotangen dari setengah sudut. Hukum ini dipakai untuk membuktikan rumus-rumus lain, seperti rumus Heron, rumus pertama Mollweide, dan rumus kedua Mollweide.
Fungsi periodik
[sunting | sunting sumber]
Fungsi-fungsi trigonometri juga penting dalam ilmu fisika. Sebagai contoh, fungsi sinus dan kosinus digunakan untuk menjelaskan gerak harmonis sederhana seperti gerakan suatu benda bermassa yang terikat pada sebuah pegas, dan gerak pendulum sederhana pada sudut yang kecil dan dengan benda bermassa yang terikat pada sebuah tali, yang keduanya merupakan pemodelan dari banyak fenomena alam. Fungsi sinus dan kosinus adalah proyeksi satu dimensi dari gerak melingkar yang seragam. Fungsi-fungsi trigonometri juga terbukti berguna dalam kajian fungsi periodik umum. Pola-pola bergelombang karakteristik dari fungsi periodik berguna dalam menggambarkan fenomena yang berulang seperti gelombang suara atau cahaya.[14]

Fungsi periodik f (x) umumnya dapat dinyatakan sebagai jumlah gelombang sinus atau gelombang kosinus dalam deret Fourier.[15] Dengan Melambangkan fungsi basis sinus atau kosinus sebagai φk, maka ekspansi dari fungsi periodik f (t) membentuk:
Sebagai contoh, fungsi dari gelombang persegi dapat ditulis sebagai deret Fourier
Dalam animasi gelombang persegi, dapat diperlihatkan bahwa hanya beberapa suku sudah menghasilkan aproksimasi yang hampir baik. Pada gambar bawah memperlihatkan superposisi dari beberapa suku dalam ekspansi gelombang geriji.
Catatan dan referensi
[sunting | sunting sumber]Catatan kaki
[sunting | sunting sumber]- ^ Kosekan terkadang juga disingkat dengan lima huruf, yaitu "cosec".
- ^ Satuan konvensional ini khususnya dipakai dalam matematika elementer.
Catatan
[sunting | sunting sumber]- ^ (Protter & Morrey 1970, hlm. APP-2, APP-3)
- ^ "Sine, Cosine, Tangent". www.mathsisfun.com. Diarsipkan dari versi asli tanggal 2023-06-30. Diakses tanggal 29 August 2020.
- ^ (Protter & Morrey 1970, hlm. APP-7)
- ^ a b Rudin, Walter, 1921–2010. Principles of mathematical analysis (edisi ke-Third). New York. ISBN 0-07-054235-X. OCLC 1502474. Diarsipkan dari versi asli tanggal 2020-01-23. Diakses tanggal 2022-08-18.
- ^ Diamond, Harvey (2014). "Defining Exponential and Trigonometric Functions Using Differential Equations". Mathematics Magazine (dalam bahasa Inggris). 87 (1): 37–42. doi:10.4169/math.mag.87.1.37. ISSN 0025-570X.
- ^ Spivak, Michael (1967). "15". Calculus. Addison-Wesley. hlm. 256–257. LCCN 67-20770.
- ^ Bityutskov, V.I. (7 February 2011). "Trigonometric Functions". Encyclopedia of Mathematics (dalam bahasa Inggris). Diarsipkan dari versi asli tanggal 29 December 2017. Diakses tanggal 29 December 2017.
- ^ Larson, Ron (2013). Trigonometry (edisi ke-9th). Cengage Learning. hlm. 153. ISBN 978-1-285-60718-4. Diarsipkan dari versi asli tanggal 15 February 2018. Extract of page 153 Diarsipkan 15 February 2018 di Wayback Machine.
- ^ See Ahlfors, pp. 43–44.
- ^ Stanley, Enumerative Combinatorics, Vol I., p. 149
- ^ Abramowitz; Weisstein.
- ^ Lambert, Johann Heinrich (2004) [1768], "Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques", dalam Berggren, Lennart; Borwein, Jonathan M.; Borwein, Peter B., Pi, a source book (edisi ke-3rd), New York: Springer-Verlag, hlm. 129–140, ISBN 0-387-20571-3
- ^ Kannappan, Palaniappan (2009). Functional Equations and Inequalities with Applications. Springer. ISBN 978-0387894911.
- ^ Farlow, Stanley J. (1993). Partial differential equations for scientists and engineers (edisi ke-Reprint of Wiley 1982). Courier Dover Publications. hlm. 82. ISBN 978-0-486-67620-3. Diarsipkan dari versi asli tanggal 20 March 2015.
- ^ See for example, Folland, Gerald B. (2009). "Convergence and completeness". Fourier Analysis and its Applications (edisi ke-Reprint of Wadsworth & Brooks/Cole 1992). American Mathematical Society. hlm. 77ff. ISBN 978-0-8218-4790-9. Diarsipkan dari versi asli tanggal 19 March 2015.
Referensi
[sunting | sunting sumber]- Templat:AS ref
- Lars Ahlfors, Complex Analysis: an introduction to the theory of analytic functions of one complex variable, second edition, McGraw-Hill Book Company, New York, 1966.
- Boyer, Carl B., A History of Mathematics, John Wiley & Sons, Inc., 2nd edition. (1991). ISBN 0-471-54397-7.
- Gal, Shmuel and Bachelis, Boris. An accurate elementary mathematical library for the IEEE floating point standard, ACM Transactions on Mathematical Software (1991).
- Joseph, George G., The Crest of the Peacock: Non-European Roots of Mathematics, 2nd ed. Penguin Books, London. (2000). ISBN 0-691-00659-8.
- Kantabutra, Vitit, "On hardware for computing exponential and trigonometric functions," IEEE Trans. Computers 45 (3), 328–339 (1996).
- Maor, Eli, Trigonometric Delights, Princeton Univ. Press. (1998). Reprint edition (2002): ISBN 0-691-09541-8.
- Needham, Tristan, "Preface"" to Visual Complex Analysis. Oxford University Press, (1999). ISBN 0-19-853446-9.
- Nielsen, Kaj L. (1966), Logarithmic and Trigonometric Tables to Five Places (edisi ke-2nd), New York: Barnes & Noble, LCCN 61-9103
- O'Connor, J. J., and E. F. Robertson, "Trigonometric functions", MacTutor History of Mathematics archive. (1996).
- O'Connor, J. J., and E. F. Robertson, "Madhava of Sangamagramma" Diarsipkan 2006-02-26 di Wayback Machine., MacTutor History of Mathematics archive. (2000).
- Pearce, Ian G., "Madhava of Sangamagramma" Diarsipkan 2006-05-05 di Wayback Machine., MacTutor History of Mathematics archive. (2002).
- Protter, Murray H.; Morrey, Charles B., Jr. (1970), College Calculus with Analytic Geometry (edisi ke-2nd), Reading: Addison-Wesley, LCCN 76087042
- Weisstein, Eric W., "Tangent" Diarsipkan 2006-07-19 di Wayback Machine. from MathWorld, diakses pada tanggal 21 Januari 2006.









































































































![{\displaystyle {\begin{aligned}\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\[6mu]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}\\[8pt]\cos x&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\[6mu]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/396790dc41b52c5381ef1683a279d05ba5d64f79)


![{\displaystyle {\begin{aligned}\tan x&{}=\sum _{n=0}^{\infty }{\frac {U_{2n+1}}{(2n+1)!}}x^{2n+1}\\[8mu]&{}=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}\left(2^{2n}-1\right)B_{2n}}{(2n)!}}x^{2n-1}\\[5mu]&{}=x+{\frac {1}{3}}x^{3}+{\frac {2}{15}}x^{5}+{\frac {17}{315}}x^{7}+\cdots ,\qquad {\text{untuk }}|x|<{\frac {\pi }{2}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed561d21f86975338cf3dc070e01b42554d7178e)
![{\displaystyle {\begin{aligned}\csc x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}2\left(2^{2n-1}-1\right)B_{2n}}{(2n)!}}x^{2n-1}\\[5mu]&=x^{-1}+{\frac {1}{6}}x+{\frac {7}{360}}x^{3}+{\frac {31}{15120}}x^{5}+\cdots ,\qquad {\text{untuk }}0<|x|<\pi .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7891f3a3f31db58fa33222e53e192e8bac9aaef)
![{\displaystyle {\begin{aligned}\sec x&=\sum _{n=0}^{\infty }{\frac {U_{2n}}{(2n)!}}x^{2n}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}\\[5mu]&=1+{\frac {1}{2}}x^{2}+{\frac {5}{24}}x^{4}+{\frac {61}{720}}x^{6}+\cdots ,\qquad {\text{untuk }}|x|<{\frac {\pi }{2}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4309690b398bbff42a01be47b59df2827e312c04)
![{\displaystyle {\begin{aligned}\cot x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}}{(2n)!}}x^{2n-1}\\[5mu]&=x^{-1}-{\frac {1}{3}}x-{\frac {1}{45}}x^{3}-{\frac {2}{945}}x^{5}-\cdots ,\qquad {\text{untuk }}0<|x|<\pi .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ba71f3cc6744076ae81ace2cc5f8487243a1630)















![{\displaystyle {\begin{aligned}\sin x&={\frac {e^{ix}-e^{-ix}}{2i}}\\[5pt]\cos x&={\frac {e^{ix}+e^{-ix}}{2}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/590e4a1bbe3ccdb7521fe06a6e5b56e538d4e729)





![{\displaystyle {\begin{aligned}\sin z&=\sin x\cosh y+i\cos x\sinh y\\[5pt]\cos z&=\cos x\cosh y-i\sin x\sinh y\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1646655eab602e234f42df85cae241ffbb867cf)




















![{\displaystyle {\begin{aligned}\sin \left(x+y\right)&=\sin x\cos y+\cos x\sin y,\\[5mu]\cos \left(x+y\right)&=\cos x\cos y-\sin x\sin y,\\[5mu]\tan(x+y)&={\frac {\tan x+\tan y}{1-\tan x\tan y}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a94648d4600a711a8851dfaea622a269be4eda5)
![{\displaystyle {\begin{aligned}\sin \left(x-y\right)&=\sin x\cos y-\cos x\sin y,\\[5mu]\cos \left(x-y\right)&=\cos x\cos y+\sin x\sin y,\\[5mu]\tan(x-y)&={\frac {\tan x-\tan y}{1+\tan x\tan y}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a627a03bba700c34bee8de20cfa09d78b127716)
![{\displaystyle {\begin{aligned}\sin 2x&=2\sin x\cos x={\frac {2\tan x}{1+\tan ^{2}x}},\\[5mu]\cos 2x&=\cos ^{2}x-\sin ^{2}x=2\cos ^{2}x-1=1-2\sin ^{2}x={\frac {1-\tan ^{2}x}{1+\tan ^{2}x}},\\[5mu]\tan 2x&={\frac {2\tan x}{1-\tan ^{2}x}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d631768e76acdd703625fbcaf9cdf8b8e3e9200f)















































