Sistem bilangan biner: Perbedaan antara revisi
k ←Suntingan 114.124.229.161 (bicara) dibatalkan ke versi terakhir oleh Ibensis Tag: Pengembalian |
Meletakkan templat under_construction. Konten dalam edit ini adalah alih bahasa dari artikel Wikipedia Bahasa Inggris en:Binary_number (oldid 1253814535); Lihat sejarahnya untuk atribusi. |
||
| (68 revisi perantara oleh 45 pengguna tidak ditampilkan) | |||
| Baris 1: | Baris 1: | ||
{{Sistem bilangan}} |
|||
{{tanpa_referensi|date=2011}} |
|||
'''{{Short description|Sistem penulisan angka menggunakan simbol 0 dan 1.}}''' |
|||
{{Under construction}} |
|||
'''Sistem bilangan biner''' atau '''sistem bilangan basis dua''' adalah sebuah [[sistem numerik|sistem penulisan angka]] dengan menggunakan dua simbol yaitu [[0 (angka)|0]] dan [[1 (angka)|1]]. Sistem bilangan biner modern ditemukan oleh [[Gottfried Wilhelm Leibniz]] pada [[abad ke-17]]. Sistem bilangan ini merupakan dasar dari semua sistem bilangan berbasis digital. Dari sistem biner, kita dapat mengkonversinya ke sistem bilangan [[Oktal]] atau [[Hexadesimal]]. Sistem ini juga dapat kita sebut dengan istilah ''[[bit]]'', atau ''Binary Digit''. Pengelompokan biner dalam komputer selalu berjumlah 8, dengan istilah '''1 Byte/[[bita]]'''. Dalam istilah komputer, 1 Byte = 8 bit. Kode-kode rancang bangun [[komputer]], seperti [[ASCII]], ''American Standard Code for Information Interchange'' menggunakan sistem peng-''kode''-an 1 Byte. |
|||
'''Sistem bilangan biner''' atau '''sistem bilangan basis dua''' adalah [[sistem numerik|sistem penulisan angka]] untuk dengan menggunakan dua simbol, umumnya "[[0 (angka)|0]]" (nol) dan "[[1 (angka)|1]]" (satu). Bilangan yang dituliskan dengan cara ini disebut dengan bilangan biner. Bilangan biner juga dapat merujuk pada [[bilangan rasional]] yang memiliki representasi terbatas dalam sistem bilangan biner. |
|||
2<sup>0</sup>=1 |
|||
Sistem bilangan biner adalah suatu [[notasi posisional]] dengan nilai basis [[2 (angka)|2]]. Setiap [[digit]] pada sistem ini disebut ''[[Bit (satuan)|bit]]'' (''binary digit''). Karena penerapannya yang mudah sebagai [[gerbang logika]] dalam [[Rangkaian elektronik|rangkaian-rangkaian elektronik]], sistem biner digunakan oleh hampir semua [[Komputer|perangkat komputer dan berbasis-komputer]] karena kesederhanaan bahasa dan kekebalannya terhadap [[derau]] (''noise'') dalam penerapan dunia nyata.<ref>{{cite web|title=3.3. Binary and Its Advantages — CS160 Reader|url=https://computerscience.chemeketa.edu/cs160Reader/Binary/Binary.html|website=computerscience.chemeketa.edu|access-date=22 May 2024}}</ref> |
|||
2<sup>1</sup>=2 |
|||
== Sejarah == |
|||
2<sup>2</sup>=4 |
|||
Sistem bilangan binear modern dipelajari di Eropa pada abad ke-16 dan 17, oleh para matematikawan meliputi [[Thomas Harriot]], [[Juan Caramuel y Lobkowitz]], dan [[Gottfried Leibniz]]. Akan tetapi, sistem-sistem yang berkaitan dengan bilangan biner sudah muncul di banyak budaya kuno, seperti Mesir, China, dan India. |
|||
=== Mesir === |
|||
2<sup>3</sup>=8 |
|||
{{See also|Matematika Mesir Kuno}} |
|||
[[Berkas:Oudjat.SVG|kiri|jmpl|240x240px|Nilai-nilai aritmetika diduga dilambangkan sebagai bagian-bagian dari [[Mata Horus]].]] |
|||
Para ahli tulis [[Mesir kuno]] menggunakan dua sistem kepenulisan yang berbeda untuk bilangan pecahan, yakni [[pecahan Mesir]] (tidak ada kaitan dengan sistem bilangan biner) dan pecahan [[Mata Horus]] (disebut demikian karena banyak sejarawan matematika percaya bahwa simbol-simbol yang digunakan dalam sistem ini dapat disusun untuk membentuk mata [[Horus]], meskipun hal ini masih diperdebatkan).<ref>{{citation|title=The Oxford Handbook of the History of Mathematics|editor1-first=Eleanor|editor1-last=Robson|editor1-link=Eleanor Robson|editor2-first=Jacqueline|editor2-last=Stedall|editor2-link=Jackie Stedall|publisher=Oxford University Press|year=2009|isbn=9780199213122|page=790|url=https://books.google.com/books?id=xZMSDAAAQBAJ&pg=PA790|contribution=Myth No. 2: the Horus eye fractions}}</ref> Pecahan Mata Horus adalah sistem bilangan biner untuk besaran-besaran pecahan dari biji-bijian, cairan, dan ukuran lainnya; dalam sistem ini satu [[hekat]] dinyatakan sebagai jumlah dari pecahan biner 1/2, 1/4, 1/8, 1/16, 1/32, dan 1/64. Bentuk awal dari sistem ini dapat ditemukan dalam dokumen-dokumen dari [[Dinasti kelima Mesir]], sekitar 2400 SM, dan bentuk [[hieroglif]] modernnya berasal dari [[Dinasti kesembilan belas Mesir]], sekitar 1200 SM.<ref>{{citation|title=Numerical Notation: A Comparative History|first=Stephen|last=Chrisomalis|publisher=Cambridge University Press|year=2010|isbn=9780521878180|pages=42–43|url=https://books.google.com/books?id=ux--OWgWvBQC&pg=PA42}}.</ref> |
|||
=== China === |
|||
2<sup>4</sup>=16 |
|||
=== Masa klasik === |
|||
2<sup>5</sup>=32 |
|||
=== India === |
|||
2<sup>6</sup>=64 |
|||
=== Afrika === |
|||
dst |
|||
=== Kebudayaan lain === |
|||
Dalam sistem komunikasi digital modern, dimana data ditransmisikan dalam bentuk bit-bit biner, dibutuhkan sistem yang tahan terhadap noise yang terdapat di kanal transmisi sehingga data yang ditransmisikan tersebut dapat diterima dengan benar. Kesalahan dalam pengiriman atau penerimaan data merupakan permasalahan yang mendasar yang memberikan dampak yang sangat signifikan pada sistem komunikasi.<ref>Erika Kusumasari Rosita, Suwadi , AchmadAnsori'', ImplementasiConvolutional Code danViterbi Decode pada DSK TMS320C6416T,'' Surabaya, </ref> |
|||
Biner yang biasa dipakai itu ada 8 digit [[angka]] dan cuma berisikan angka 1 dan 0, tidak ada angka lainnya. |
|||
== |
=== Eropa pra-Leibniz === |
||
=== Leibniz === |
|||
=== Perkembangan selanjutnya === |
|||
== Kepenulisan == |
|||
== Mencacah dalam biner == |
|||
=== Mencacah dalam sistem desimal === |
|||
''pendahuluan'' |
|||
=== Mencacah dalam sistem biner === |
|||
== Pecahan == |
|||
== Aritmetika biner == |
|||
=== Penambahan === |
|||
=== Pengurangan === |
|||
{{further|Bilangan biner bertanda|Komplemen dua}} |
|||
: |
|||
=== Perkalian === |
|||
=== Pembagian === |
|||
{{See also|Division algorithm#Integer division (unsigned) with remainder}} |
|||
=== Akar kuadrat === |
|||
== Operasi bitwise == |
|||
{{Main|Bitwise operation}} |
|||
== Konversi dari dan ke sistem bilangan lainnya == |
|||
{| class="wikitable" |
{| class="wikitable" |
||
|- |
|- |
||
| Baris 28: | Baris 68: | ||
! Biner (8 bit) |
! Biner (8 bit) |
||
|- |
|- |
||
| |
|- 69 |
||
| 0000 0000 |
| 0000 0000 |
||
|- |
|- |
||
|1 |
|1 |
||
| 0000 0001 |
| 0000 0001 |
||
|- |
|- |
||
|2 |
|2 |
||
| Baris 93: | Baris 133: | ||
|21 |
|21 |
||
|0001 0101 |
|0001 0101 |
||
|- |
|||
|22 |
|||
|0001 0110 |
|||
|- |
|- |
||
|23 |
|23 |
||
| Baris 121: | Baris 164: | ||
=== Dari Biner ke Desimal === |
=== Dari Biner ke Desimal === |
||
[[Berkas:Danycopyan.png|jmpl|395x395px]] |
[[Berkas:Danycopyan.png|jmpl|395x395px]] |
||
Untuk setiap bilangan biner dengan <math>n</math> digit: |
|||
<big>{{math|''d''<sub>''n-1''</sub>, ''...'' ''d''<sub>''3''</sub>, ''d''<sub>''2''</sub>, ''d''<sub>''1''</sub>, ''d''<sub>''0''</sub>}}</big> |
Untuk setiap bilangan biner dengan <math>n</math> digit: <big>{{math|''d''<sub>''n-1''</sub>, ''...'' ''d''<sub>''3''</sub>, ''d''<sub>''2''</sub>, ''d''<sub>''1''</sub>, ''d''<sub>''0''</sub>}}</big> |
||
Bilangan desimalnya adalah hasil penjumlahan dari digit biner (<math>d_n</math>) dikalikan dengan pangkat 2 nya (<math>2^n</math>): |
Bilangan desimalnya adalah hasil penjumlahan dari digit biner (<math>d_n</math>) dikalikan dengan pangkat 2 nya (<math>2^n</math>): |
||
<big>{{math|''decimal'' {{=}} ''d''<sub>''0''</sub> ''×'' ''2''<sup>''0''</sup> + ''d''<sub>''1''</sub> ''×'' ''2''<sup>''1''</sup> + ''d''<sub>''2''</sub> ''×'' ''2''<sup>''2''</sup> + ''...''}}</big> |
|||
<big>{{math|''decimal'' {{=}} ''d''<sub>''0''</sub> ''×'' ''2''<sup>''0''</sup> + ''d''<sub>''1''</sub> ''×'' ''2''<sup>''1''</sup> + ''d''<sub>''2''</sub> ''×'' ''2''<sup>''2''</sup> + ''...''}}</big> |
|||
Contoh: |
Contoh: |
||
Tabel dibawah ini menunjukkan konversi bilangan biner 01010101 menjadi [[desimal]]. |
|||
Tabel dibawah ini menunjukkan konversi bilangan biner 01010101 menjadi desimal. |
|||
{| class="wikitable" style="text-align: center;" |
{| class="wikitable" style="text-align: center;" |
||
|- |
|- |
||
| Baris 152: | Baris 192: | ||
=== Dari Desimal ke Biner === |
=== Dari Desimal ke Biner === |
||
{{Sub-rapikan}} |
{{Sub-rapikan}} |
||
Desimal = 10 |
Desimal = 10 |
||
Bilangan yang mendekati 10 adalah 8 (2<sup>3</sup>), selanjutnya hasil pengurangan 10-8 = 2 (2<sup>1</sup>) |
Bilangan yang mendekati 10 adalah 8 (2<sup>3</sup>), selanjutnya hasil pengurangan 10-8 = 2 (2<sup>1</sup>), sehingga dapat dijabarkan seperti berikut: |
||
10 = ('''1''' x 2<sup>3</sup>) + ('''0''' x 2<sup>2</sup>) + ('''1''' x 2<sup>1</sup>) + ('''0''' x 2<sup>0</sup>) |
10 = ('''1''' x 2<sup>3</sup>) + ('''0''' x 2<sup>2</sup>) + ('''1''' x 2<sup>1</sup>) + ('''0''' x 2<sup>0</sup>) |
||
Dari perhitungan di atas bilangan biner dari 10 adalah 1010. |
|||
Dapat juga dengan cara lain yaitu 10: 2 = 5 sisa '''0''' (0 akan menjadi angka terakhir dalam bilangan biner), |
|||
5 (hasil pembagian pertama): 2 = 2 sisa '''1''' (1 akan menjadi angka kedua terakhir dalam bilangan biner), |
|||
atau dengan cara yang singkat |
|||
2 (hasil pembagian kedua): 2 = 1 sisa '''0''' (0 akan menjadi angka ketiga terakhir dalam bilangan biner), |
|||
1(hasil pembagian ketiga): 2 = 0 sisa '''1''' (1 akan menjadi angka pertama dalam bilangan biner) karena hasil bagi sudah 0 atau habis, sehingga bilangan biner dari '''10''' = '''1010'''. |
|||
Atau dengan cara yang singkat: |
|||
10:2=5('''0'''), |
10:2=5('''0'''), |
||
| Baris 170: | Baris 216: | ||
2:2=1('''0'''), |
2:2=1('''0'''), |
||
1:2=0('''1''') sisa hasil bagi dibaca dari belakang menjadi '''1010''' |
1:2=0('''1''') sisa hasil bagi dibaca dari belakang menjadi '''1010'''. |
||
== |
=== Desimal ke biner === |
||
Citra biner (binary image) adalah citra yang hanya mempunyai dua nilai derajat: Meskipun saat ini citra berwarna lebih disukai karena memberi kesan yang lebih kaya dari pada citra biner, namun tidak membuat citra biner mati. Pada beberapa aplikasi citra biner masih tetap dibutuhkan, misalnya citra logo instansi (yang hanya terdiri atas warna hitam dan putih), citra kode batang (bar code) yang tertera pada label barang, citra hasil pemindahan dokumen teks, dan sebagainya. |
|||
=== Biner ke desimal === |
|||
=== Heksadesimal === |
|||
{{Main|Heksadesimal}} |
|||
=== Oktal === |
|||
{{Main|Oktal}} |
|||
: |
|||
: |
|||
== Merepresentasikan bilangan riil == |
|||
== Contoh penerapan == |
|||
=== Pengenalan Warna Citra Biner === |
|||
Citra biner (binary image) adalah citra yang hanya mempunyai dua nilai derajat: Meskipun saat ini citra berwarna lebih disukai karena memberi kesan yang lebih kaya daripada [[citra biner]], namun tidak membuat citra biner mati. Pada beberapa aplikasi citra biner masih tetap dibutuhkan, misalnya citra logo instansi (yang hanya terdiri atas warna hitam dan putih), citra [[kode batang]] (bar code) yang tertera pada label barang, citra hasil pemindahan dokumen teks, dan sebagainya. |
|||
objek di dalam citra biner adalah segmentasi objek. Proses segmentasi bertujuan mengelompokkan pixel-pixel objek menjadi wilayah (region) yang merepresentasikan objek. Ada dua pendekatan yang digunakan dalam segmentasi objek: |
objek di dalam citra biner adalah segmentasi objek. Proses segmentasi bertujuan mengelompokkan pixel-pixel objek menjadi wilayah (region) yang merepresentasikan objek. Ada dua pendekatan yang digunakan dalam segmentasi objek: |
||
# Segmentasi berdasarkan batas wilayah (tepidariobjek). Pixel-pixel tepi ditelusuri sehingga rangkaian |
# Segmentasi berdasarkan batas wilayah (tepidariobjek). Pixel-pixel tepi ditelusuri sehingga rangkaian piksel yang menjadi batas (boundary) antara objek dengan latar belakang dapat diketahui secara keseluruhan ([[Algoritma|algoritme]] boundary following). |
||
# Segmentasi kebentuk-bentuk dasar (misalnya segmentasi huruf menjadi garis-garis vertikal dan horizontal, segmentasi objek menjadi bentuk lingkaran, elips, |
# Segmentasi kebentuk-bentuk dasar (misalnya segmentasi huruf menjadi garis-garis vertikal dan horizontal, segmentasi objek menjadi bentuk lingkaran, elips, dan sebagainya). |
||
== Pranala luar == |
|||
{{Commons category|Binary numeral system}}{{Wikibooks|Fractals/Mathematics/binary}} |
|||
* [http://www.cut-the-knot.org/do_you_know/BinaryHistory.shtml Binary System] at [[cut-the-knot]] |
|||
* [http://www.cut-the-knot.org/blue/frac_conv.shtml Conversion of Fractions] at [[cut-the-knot]] |
|||
* Sir Francis Bacon's BiLiteral Cypher system {{Webarchive|url=https://web.archive.org/web/20160923014940/http://www.baconlinks.com/docs/BILITERAL.doc|date=23 September 2016}}, predates binary number system. |
|||
{| class="wikitable" |
|||
|- |
|||
|} |
|||
== Referensi == |
== Referensi == |
||
{{reflist}} |
{{reflist}} |
||
{{Authority control}} |
|||
{{matematika-stub}} |
|||
[[Kategori:Sistem bilangan|Biner]] |
[[Kategori:Sistem bilangan|Biner]] |
||
Revisi terkini sejak 3 November 2024 00.11
| Sistem bilangan | ||||||
|---|---|---|---|---|---|---|

| ||||||
| Daftar sistem bilangan |
'
Halaman ini sedang dipersiapkan dan dikembangkan sehingga mungkin terjadi perubahan besar. Anda dapat membantu dalam penyuntingan halaman ini. Halaman ini terakhir disunting oleh Kekavigi (Kontrib • Log) 15 hari 1310 menit lalu. Jika Anda melihat halaman ini tidak disunting dalam beberapa hari, mohon hapus templat ini. |
Sistem bilangan biner atau sistem bilangan basis dua adalah sistem penulisan angka untuk dengan menggunakan dua simbol, umumnya "0" (nol) dan "1" (satu). Bilangan yang dituliskan dengan cara ini disebut dengan bilangan biner. Bilangan biner juga dapat merujuk pada bilangan rasional yang memiliki representasi terbatas dalam sistem bilangan biner.
Sistem bilangan biner adalah suatu notasi posisional dengan nilai basis 2. Setiap digit pada sistem ini disebut bit (binary digit). Karena penerapannya yang mudah sebagai gerbang logika dalam rangkaian-rangkaian elektronik, sistem biner digunakan oleh hampir semua perangkat komputer dan berbasis-komputer karena kesederhanaan bahasa dan kekebalannya terhadap derau (noise) dalam penerapan dunia nyata.[1]
Sejarah
[sunting | sunting sumber]Sistem bilangan binear modern dipelajari di Eropa pada abad ke-16 dan 17, oleh para matematikawan meliputi Thomas Harriot, Juan Caramuel y Lobkowitz, dan Gottfried Leibniz. Akan tetapi, sistem-sistem yang berkaitan dengan bilangan biner sudah muncul di banyak budaya kuno, seperti Mesir, China, dan India.
Mesir
[sunting | sunting sumber]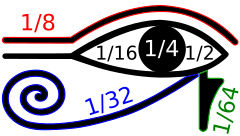
Para ahli tulis Mesir kuno menggunakan dua sistem kepenulisan yang berbeda untuk bilangan pecahan, yakni pecahan Mesir (tidak ada kaitan dengan sistem bilangan biner) dan pecahan Mata Horus (disebut demikian karena banyak sejarawan matematika percaya bahwa simbol-simbol yang digunakan dalam sistem ini dapat disusun untuk membentuk mata Horus, meskipun hal ini masih diperdebatkan).[2] Pecahan Mata Horus adalah sistem bilangan biner untuk besaran-besaran pecahan dari biji-bijian, cairan, dan ukuran lainnya; dalam sistem ini satu hekat dinyatakan sebagai jumlah dari pecahan biner 1/2, 1/4, 1/8, 1/16, 1/32, dan 1/64. Bentuk awal dari sistem ini dapat ditemukan dalam dokumen-dokumen dari Dinasti kelima Mesir, sekitar 2400 SM, dan bentuk hieroglif modernnya berasal dari Dinasti kesembilan belas Mesir, sekitar 1200 SM.[3]
China
[sunting | sunting sumber]Masa klasik
[sunting | sunting sumber]India
[sunting | sunting sumber]Afrika
[sunting | sunting sumber]Kebudayaan lain
[sunting | sunting sumber]Eropa pra-Leibniz
[sunting | sunting sumber]Leibniz
[sunting | sunting sumber]Perkembangan selanjutnya
[sunting | sunting sumber]Kepenulisan
[sunting | sunting sumber]Mencacah dalam biner
[sunting | sunting sumber]Mencacah dalam sistem desimal
[sunting | sunting sumber]pendahuluan
Mencacah dalam sistem biner
[sunting | sunting sumber]Pecahan
[sunting | sunting sumber]Aritmetika biner
[sunting | sunting sumber]Penambahan
[sunting | sunting sumber]Pengurangan
[sunting | sunting sumber]Perkalian
[sunting | sunting sumber]Pembagian
[sunting | sunting sumber]Akar kuadrat
[sunting | sunting sumber]Operasi bitwise
[sunting | sunting sumber]Konversi dari dan ke sistem bilangan lainnya
[sunting | sunting sumber]| Desimal | Biner (8 bit) |
|---|---|
| 0000 0000 | |
| 1 | 0000 0001 |
| 2 | 0000 0010 |
| 3 | 0000 0011 |
| 4 | 0000 0100 |
| 5 | 0000 0101 |
| 6 | 0000 0110 |
| 7 | 0000 0111 |
| 8 | 0000 1000 |
| 9 | 0000 1001 |
| 10 | 0000 1010 |
| 11 | 0000 1011 |
| 12 | 0000 1100 |
| 13 | 0000 1101 |
| 14 | 0000 1110 |
| 15 | 0000 1111 |
| 16 | 0001 0000 |
| 17 | 0001 0001 |
| 18 | 0001 0010 |
| 19 | 0001 0011 |
| 20 | 0001 0100 |
| 21 | 0001 0101 |
| 22 | 0001 0110 |
| 23 | 0001 0111 |
| 24 | 0001 1000 |
| 25 | 0001 1001 |
| 26 | 0001 1010 |
| 27 | 0001 1011 |
| 28 | 0001 1100 |
| 29 | 0001 1101 |
| 30 | 0001 1110 |
Dari Biner ke Desimal
[sunting | sunting sumber]
Untuk setiap bilangan biner dengan digit: dn-1, ... d3, d2, d1, d0
Bilangan desimalnya adalah hasil penjumlahan dari digit biner () dikalikan dengan pangkat 2 nya (): decimal = d0 × 20 + d1 × 21 + d2 × 22 + ...
Contoh: Tabel dibawah ini menunjukkan konversi bilangan biner 01010101 menjadi desimal.
| Biner (d) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|
| n | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 2n | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| dn x 2n | 0 x 128 | 1 x 64 | 0 x 32 | 1 x 16 | 0 x 8 | 1 x 4 | 0 x 2 | 1 x 1 |
| 64 + 16 + 4 + 1 = 85 | ||||||||
Diperoleh hasil akhir bahwa 010101012 = 8510.
Dari Desimal ke Biner
[sunting | sunting sumber]Bagian artikel ini perlu dirapikan. Bantulah kami untuk melakukannya. |
Desimal = 10
Bilangan yang mendekati 10 adalah 8 (23), selanjutnya hasil pengurangan 10-8 = 2 (21), sehingga dapat dijabarkan seperti berikut:
10 = (1 x 23) + (0 x 22) + (1 x 21) + (0 x 20)
Dari perhitungan di atas bilangan biner dari 10 adalah 1010.
Dapat juga dengan cara lain yaitu 10: 2 = 5 sisa 0 (0 akan menjadi angka terakhir dalam bilangan biner),
5 (hasil pembagian pertama): 2 = 2 sisa 1 (1 akan menjadi angka kedua terakhir dalam bilangan biner),
2 (hasil pembagian kedua): 2 = 1 sisa 0 (0 akan menjadi angka ketiga terakhir dalam bilangan biner),
1(hasil pembagian ketiga): 2 = 0 sisa 1 (1 akan menjadi angka pertama dalam bilangan biner) karena hasil bagi sudah 0 atau habis, sehingga bilangan biner dari 10 = 1010.
Atau dengan cara yang singkat:
10:2=5(0),
5:2=2(1),
2:2=1(0),
1:2=0(1) sisa hasil bagi dibaca dari belakang menjadi 1010.
Desimal ke biner
[sunting | sunting sumber]Biner ke desimal
[sunting | sunting sumber]Heksadesimal
[sunting | sunting sumber]Oktal
[sunting | sunting sumber]Merepresentasikan bilangan riil
[sunting | sunting sumber]Contoh penerapan
[sunting | sunting sumber]Pengenalan Warna Citra Biner
[sunting | sunting sumber]Citra biner (binary image) adalah citra yang hanya mempunyai dua nilai derajat: Meskipun saat ini citra berwarna lebih disukai karena memberi kesan yang lebih kaya daripada citra biner, namun tidak membuat citra biner mati. Pada beberapa aplikasi citra biner masih tetap dibutuhkan, misalnya citra logo instansi (yang hanya terdiri atas warna hitam dan putih), citra kode batang (bar code) yang tertera pada label barang, citra hasil pemindahan dokumen teks, dan sebagainya.
objek di dalam citra biner adalah segmentasi objek. Proses segmentasi bertujuan mengelompokkan pixel-pixel objek menjadi wilayah (region) yang merepresentasikan objek. Ada dua pendekatan yang digunakan dalam segmentasi objek:
- Segmentasi berdasarkan batas wilayah (tepidariobjek). Pixel-pixel tepi ditelusuri sehingga rangkaian piksel yang menjadi batas (boundary) antara objek dengan latar belakang dapat diketahui secara keseluruhan (algoritme boundary following).
- Segmentasi kebentuk-bentuk dasar (misalnya segmentasi huruf menjadi garis-garis vertikal dan horizontal, segmentasi objek menjadi bentuk lingkaran, elips, dan sebagainya).
Pranala luar
[sunting | sunting sumber]- Binary System at cut-the-knot
- Conversion of Fractions at cut-the-knot
- Sir Francis Bacon's BiLiteral Cypher system Diarsipkan 23 September 2016 di Wayback Machine., predates binary number system.
Referensi
[sunting | sunting sumber]- ^ "3.3. Binary and Its Advantages — CS160 Reader". computerscience.chemeketa.edu. Diakses tanggal 22 May 2024.
- ^ Robson, Eleanor; Stedall, Jacqueline, ed. (2009), "Myth No. 2: the Horus eye fractions", The Oxford Handbook of the History of Mathematics, Oxford University Press, hlm. 790, ISBN 9780199213122
- ^ Chrisomalis, Stephen (2010), Numerical Notation: A Comparative History, Cambridge University Press, hlm. 42–43, ISBN 9780521878180.



