Teorema Taylor

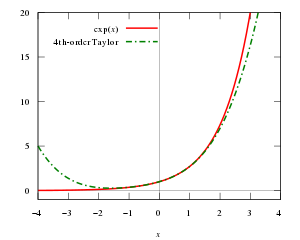
Fungsi eksponensial $y=e^{x}$ (garis merah kontinu) dan polinomial Taylor orde empat di sekitar titik asal (garis hijau putus-putus)

Dalam kalkulus, teorema Taylor memberikan barisan pendekatan sebuah fungsi yang diferensiabel pada sebuah titik menggunakan suku banyak (polinomial). Koefisien polinomial tersebut hanya tergantung pada turunan fungsi pada titik yang bersangkutan. Teorema ini juga memberikan estimasi besarnya galat dari pendekatan itu. Teorema ini mendapat nama dari matematikawan Brook Taylor, yang menyatakannya pada tahun 1712, meskipun hasilnya sudah ditemukan pertama kali tahun 1671 oleh James Gregory

Teorema Taylor dalam satu variabel

Teorema Taylor menyatakan sembarang fungsi mulus dapat dihampiri dengan polinomial. Contoh sederhana penerapan teorema Taylor adalah hampiran fungsi eksponensial e^x di dekat x = 0:

${\textrm {e}}^{x}\approx 1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots +{\frac {x^{n}}{n!}}.$

Hampiran ini dinamakan hampiran Taylor orde ke-n' terhadap e^x karena menghampiri nilai fungsi eksponensial menggunakan polinomial derajat n. Hampiran ini hanya berlaku untuk x mendekati nol, dan bila x bergerak menjauhi nol, hampiran ini menjadi semakin buruk. Kualitas hampiran dinyatakan oleh suku sisa:

$R_{n}(x)={\textrm {e}}^{x}-\left(1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots +{\frac {x^{n}}{n!}}\right).$

Lebih umum lagi, teorema Taylor berlaku untuk setiap fungsi yang dapat diturunkan ƒ, dengan hampiran untuk x di dekat titik a, dalam bentuk:

$f(x)\approx f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\dots {\frac {f^{(n)}(a)}{n!}}(x-a)^{n}.$

Suku sisa adalah perbedaan antara fungsi dan polinomial hampirannya:

$R_{n}(x)=f(x)-\left(f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\dots {\frac {f^{(n)}(a)}{n!}}(x-a)^{n}\right).$

Meskipun rumus eksplisit untuk suku sisa ini jarang digunakan, teorema Taylor juga memberikan estimasi nilai sisanya. Dengan kata lain, untuk x cukup dekat terhadap a, suku sisa haruslah cukup kecil. Teorema Taylor memberikan informasi persis seberapa kecil suku sisa tersebut.

Pranala luar

• (Inggris)Trigonometric Taylor Expansion Applet demonstrasi interaktif
• (Inggris)Taylor Series Revisited pada Holistic Numerical Methods Institute