Monad (teori kategori)

Artikel ini bukan mengenai Monad (aljabar linear).

Untuk penggunaan monad dalam perangkat lunak komputer, lihat monads dalam pemrograman fungsional.

Dalam teori kategori, cabang dari matematika, monad (juga disebut tripel, triad, konstruksi standar dan konstruksi dasar) adalah endofunktor (funktor memetakan kategori), dengan dua transformasi alam yang dibutuhkan untuk memenuhi kondisi koherensi. Monad digunakan dalam teori funktor adjoin, dan mereka menggeneralisasi operator penutupan pada himpunan terurut parsial ke kategori arbitrer.

Pendahuluan dan definisi

Monad adalah jenis endofunktor tertentu. Misalnya, jika $F$ dan $G$ adalah sepasang funktor adjoin, dengan $F$ di sebelah kiri adjoint ke $G$, maka komposisi $G\circ F$ adalah monad. Jika $F$ dan $G$ adalah fungsi invers, monad terkait adalah identitas funktor. Secara umum, tambahan bukanlah kesetaraan, mereka menghubungkan kategori dengan sifat yang berbeda. Teori monad penting sebagai bagian dari upaya untuk 'mencari' tambahan. Separuh teori lainnya, dari dipelajari juga dari pertimbangan $F\circ G$, dibahas di bawah teori ganda komonad .

Definisi formal

Sepanjang artikel ini $C$ menunjukkan sebuah kategori. Sebuah monad di $C$ terdiri dari endofunktor $T\colon C\to C$ bersama dengan dua transformasi alami: $\eta \colon 1_{C}\to T$ (dimana $1_{C}$ menunjukkan fungsi identitas pada $C$) dan $\mu \colon T^{2}\to T$ (dimana $T^{2}$ adalah funktor $T\circ T$ dari $C$ ke $C$). Ini diperlukan untuk memenuhi ketentuan berikut (terkadang disebut kondisi koherensi):

• $\mu \circ T\mu =\mu \circ \mu T$ (sebagai transformasi $T^{3}\to T$);
• $\mu \circ T\eta =\mu \circ \eta T=1_{T}$ (sebagai transformasi $T\to T$; maka $1_{T}$ menunjukkan transformasi identitas dari $T$ menjadi $T$).

Kita dapat menulis ulang kondisi ini menggunakan diagram komutatif berikut:

Lihat artikel tentang transformasi natural untuk penjelasan tentang notasi $T\mu$ dan $\mu T$, atau lihat di bawah diagram komutatif yang tidak menggunakan pengertian ini:

Aksioma pertama mirip dengan asosiativitas dalam monoid jika $\mu$ sebagai operasi biner monoid, dan aksioma kedua mirip dengan keberadaan elemen identitas (diberikan $\eta$). Monad pada $C$ dapat didefinisikan sebagai alternatif sebagai monoid dalam kategori $\mathbf {End} _{C}$ yang objeknya merupakan endofunktor dari $C$ dan yang morfismenya merupakan transformasi, dengan struktur monoid yang disebabkan oleh komposisi endofungtor.

Himpunan daya monad

Himpunan daya monad adalah monad ${\mathcal {P}}$ pada kategori $\mathbf {Himpunan}$: Untuk himpunan $A$ biarkan $T(A)$ menjadi himpunan daya dari $A$ dan untuk sebuah fungsi $f\colon A\to B$ biarkan $T(f)$ menjadi fungsi antara set daya yang diinduksi dengan galeri langsung di bawah $f$. Untuk setiap set $A$, peta $\eta _{A}\colon A\to T(A)$, pada $a\in A$ tunggal $\{a\}$. The function

$\mu _{A}\colon T(T(A))\to T(A)$

mengambil satu set himpunan ke satuan. Data ini menggambarkan sebuah monad.

Keterangan

Aksioma sebuah monad secara formal mirip dengan aksioma monoid. Faktanya, monad adalah kasus khusus dari monoid, yaitu mereka merupakan monoid di antara endofunktor $\operatorname {End} (C)$, yang dilengkapi dengan perkalian yang diberikan oleh komposisi endofungtor.

Komposisi monad secara umum bukan monad. Misalnya, monad himpunan daya ganda ${\mathcal {P}}\circ {\mathcal {P}}$ tidak menerima struktur monad.

Sejarah terminologis

Gagasan monad ditemukan oleh Roger Godement pada tahun 1958 dengan nama "konstruksi standar". Pada 1960-an dan 1970-an, banyak orang menggunakan nama "tiga kali lipat". Istilah standar sekarang "monad" adalah karena Saunders Mac Lane.

Contoh

Monad arising dari tambahan

Semua adjunsi

$F:C\rightleftarrows D:G$

menimbulkan monad pada C . Konstruksi yang sangat luas ini bekerja sebagai berikut: ujung ujung adalah komposit

$T=G\circ F.$

Fungsi akhir ini dengan cepat dianggap sebagai monad, di mana peta satuan berasal dari peta satuan $\operatorname {id} _{C}\to G\circ F$ dari adjunsi, dan peta perkalian dibangun menggunakan peta mounit dari adjunsi:

$T^{2}=G\circ F\circ G\circ F{\stackrel {G\circ {\text{kounit}}\circ F}{\to }}G\circ F=T.$

Dualisasi ganda

Dualisasi monad , untuk bidang k tetap muncul dari adjunsi

$(-)^{*}:\mathbf {Vekt} _{k}\rightleftarrows \mathbf {Vekt} _{k}^{op}:(-)^{*}$

di mana kedua fungsi diberikan dengan mengirimkan ruang vektor V ke ruang vektor ganda $V^{*}:=\operatorname {Hom} (V,k)$. Monad terkait mengirimkan ruang vektor V ke dual ganda $V^{**}$. Monad ini dibahas secara umum oleh (Kock 1970).

Operator penutupan himpunan urutan sebagian

Untuk kategori yang timbul dari himpunan terurut parsial $(P,\leq )$ (dengan morfisme tunggal dari $x$ to $y$ iff $x\leq y$), maka formalismenya menjadi lebih sederhana: bagian adjoin adalah koneksi Galois dan monad adalah operator penutupan.

Adjunsi foget bebas

Misalnya, karena $G$ menjadi funktor fogetful dari kategori Grp dari grup ke kategori Himpunan, dan maka $F$ menjadi fungsi grup bebas dari kategori himpunan ke kategori grup. Kemudian $F$ adalah ujung kiri dari $G$. Dalam hal ini, monad terkait $T=G\circ F$ maka himpunan $X$ dan himpunan yang mendasari dari grup bebas $\mathrm {Bebas} (X)$. Peta satuan monad ini diberikan oleh peta

$X\rightarrow T(X)$

termasuk set apapun $X$ ke dalam himpunan $\mathrm {Bebas} (X)$ dengan cara alami, sebagai pita panjang 1. Selanjutnya, perkalian dari monad ini adalah peta

$T(T(X))\rightarrow T(X)$

terbuat dari rangkaian atau 'perataan' alami dari 'pita'. Maka berarti dua transformasi natural. Contoh sebelumnya tentang grup bebas dapat digeneralisasikan ke semua jenis aljabar dalam arti Varietas aljabar dalam aljabar universal. Jadi, setiap jenis aljabar menimbulkan monad pada kategori himpunan. Yang penting, jenis aljabar dapat dipulihkan dari monad (sebagai kategori aljabar Eilenberg–Moore), jadi monad juga dapat dilihat sebagai varietas umum dari aljabar universal.

Monad lain yang muncul dari sebuah adjunsi adalah saat $T$ adalah ujung fungsi pada kategori ruang vektor yang memetakan ruang vektor $V$ ke aljabar tensor $T(V)$, dan yang memetakan peta linier ke produk tensornya. Kami kemudian memiliki transformasi alami yang sesuai dengan penyematan $V$ ke dalam aljabar tensor, dan transformasi alami yang sesuai dengan peta dari $T(T(V))$ untuk $T(V)$ diperoleh hanya dengan memperluas semua produk tensor.

Monad kondensi

Di bawah kondisi ringan, funktor yang tidak menggunakan adjoin kiri juga menghasilkan monad, yang disebut monad kondensi. Misalnya, inklusi

$\mathbf {FinHimpunan} \subset \mathbf {Himpunan}$

tidak menerima adjoint kiri. Codensity monadnya adalah monad pada set yang mengirimkan set X ke set ultrafilter pada X . Maka, contoh serupa dibahas oleh (Leinster 2013).

Aljabar untuk monad

Lihat pula: Aljabar-F dan Pseudoaljabar

Dirumuskan monad $(T,\eta ,\mu )$ pada kategori $C$, wajar untuk mempertimbangkan aljabar-$T$ , yaitu, objek C yang dilanjutkan dari T ke cara yang kompatibel dengan satuan dan perkalian monad. Lebih formal, aljabar- T pada $(x,h)$ adalah objek $x$ dari $C$ dengan panah $h\colon Tx\to x$ of $C$ disebut peta struktur dari aljabar seperti diagram

dan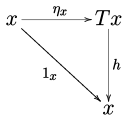

Morfisme $f\colon (x,h)\to (x',h')$ dari aljabar-$T$ adalah panah $f\colon x\to x'$ dari $C$ dari diagram

T membentuk kategori yang disebut kategori Eilenberg–Moore dan dilambangkan dengan $C^{T}$. Misalnya, untuk grup bebas monad yang didiskusikan di atas, aljabar- T adalah himpunan X bersama dengan peta dari grup bebas yang dihasilkan oleh X menuju X dengan subjek asosiatif dan satuan. Struktur seperti itu setara dengan mengatakan bahwa X adalah kelompok itu sendiri.

Contoh lain adalah distribusi monad pada kategori himpunan. Hal tersebut ditentukan dengan urutan satu himpunan X ke himpunan fungsi $f:X\to [0,1]$ dengan dukungan terbatas dan sehingga $\sum _{x\in X}f(x)=1$. Dengan memeriksa definisi, dapat ditunjukkan bahwa aljabar di atas monad distribusi setara dengan himpunan konveks, yaitu, himpunan dengan operasi $x+_{r}y$ pada $r\in [0,1]$ tunduk pada aksioma yang menyerupai perilaku kombinasi linear cembung $rx+(1-r)y$ dalam ruang Euklides.

Penggunaan

Monad digunakan dalam pemrograman fungsional untuk mengekspresikan jenis komputasi sekuensial (terkadang dengan efek samping). Lihat monad dalam pemrograman fungsional, dan modul Wikibuku yang lebih berorientasi matematis Teori Haskell/Kategori.

Dalam logika kategoris, sebuah analogi telah ditarik antara teori monad-komonad, dan logika modal melalui operator penutupan, aljabar interior, dan hubungannya dengan model dari S4 dan logika intuisi.

Generalisasi

Dimungkinkan untuk mendefinisikan monad dalam Kategori-2 $C$. Monad yang dijelaskan di atas adalah monad untuk $C=\mathbf {Cat}$.

Lihat pula

• Hukum distributif antara monad
• Teori Lawvere
• Monad (pemrograman fungsional)
• Poliad
• Monad kekuatan

Bacaan lebih lanjut

• Barr, Michael; Wells, Charles (1999), Category Theory for Computing Science (PDF) 
• Godement, Roger (1958), Topologie Algébrique et Théorie des Faisceaux., Actualités Sci. Ind., Publ. Math. Univ. Strasbourg, 1252 (13), Paris: Hermann, hlm. viii+283 pp 
• Kock, Anders (1970), "On Double Dualization Monads", Mathematica Scandinavica, 27: 151, doi:10.7146/math.scand.a-10995  
• Leinster, Tom (2013), "Codensity and the ultrafilter monad", Theory and Applications of Categories, 28: 332–370, arXiv:1209.3606 , Bibcode:2012arXiv1209.3606L 
• MacLane, Saunders (1978), Categories for the Working Mathematician, Graduate Texts in Mathematics, 5, doi:10.1007/978-1-4757-4721-8 , ISBN 978-1-4419-3123-8 
• Pedicchio, Maria Cristina; Tholen, Walter, ed. (2004). Categorical Foundations. Special Topics in Order, Topology, Algebra, and Sheaf Theory. Encyclopedia of Mathematics and Its Applications. 97. Cambridge: Cambridge University Press. ISBN 0-521-83414-7. Zbl 1034.18001. 
• Riehl, Emily (2017), Category Theory in Context, ISBN 9780486820804 
• Turi, Daniele (1996–2001), Category Theory Lecture Notes (PDF) 

Pranala luar

• Monad, lima ceramah singkat (dengan satu lampiran).
• John Baez's This Week's Finds in Mathematical Physics (Week 89) mencakup monad dalam 2 kategori.