Konsentris: Perbedaan antara revisi
Tampilan
Konten dihapus Konten ditambahkan
k Bot: perubahan kosmetika |
k Bot: obyek → objek (bentuk baku) |
||
| Baris 1: | Baris 1: | ||
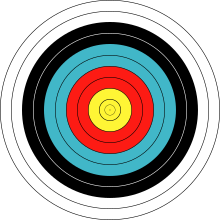
[[Berkas:WA 80 cm archery target.svg|thumb|Sebuah [[target tembak|target panahan]], menampilkan lingkaran konsentris yang dikelilingi [[mata banteng (target)|mata banteng]]".]] |
[[Berkas:WA 80 cm archery target.svg|thumb|Sebuah [[target tembak|target panahan]], menampilkan lingkaran konsentris yang dikelilingi [[mata banteng (target)|mata banteng]]".]] |
||
[[Berkas:Kepler-solar-system-2.png|thumb|Model kosmologi Kepler dibentuk oleh bola kosentris dan polihedra biasa]] |
[[Berkas:Kepler-solar-system-2.png|thumb|Model kosmologi Kepler dibentuk oleh bola kosentris dan polihedra biasa]] |
||
Dalam [[geometri]], dua [[ |
Dalam [[geometri]], dua [[objek matematika|objek]] atau lebih dikatakan sebagai '''konsentris''', '''koaksal''', atau '''koaksial''' saat mereka berbagi [[pusat (geometri)|pusat]] atau [[poros koordinat|poros]] yang sama. [[Lingkaran]],<ref>{{citation|title=Elementary Geometry for College Students|first1=Daniel C.|last1=Alexander|first2=Geralyn M.|last2=Koeberlein|year=2009|publisher=Cengage Learning|isbn=9781111788599|page=279|url=https://books.google.com/books?id=cRIFAAAAQBAJ&pg=PA279}}.</ref> [[poligon biasa]]<ref>{{citation|title=A Course of Pure Mathematics|first=Godfrey Harold|last=Hardy|author-link=G. H. Hardy|publisher=The University Press|year=1908|page=107|url=https://books.google.com/books?id=tUY7AQAAIAAJ&pg=PA107}}.</ref> dan [[polihedron biasa|polihedra biasa]],<ref>{{citation|title=Comprehensive Coordination Chemistry: Theory & background|first=Robert D.|last=Gillard|isbn=9780080262321|pages=[https://archive.org/details/comprehensivecoo0001unse/page/137 137, 139]|publisher=Pergamon Press|year=1987|url=https://archive.org/details/comprehensivecoo0001unse/page/137}}.</ref> dan [[bola (geometri)|bola]]<ref name="apostol"/> dapat menjadi kosentris satu sama lain (berbagi titik pusat yang sama), karena bersifat [[Silinder (geometri)|silinder]]<ref>{{citation|title=Fluid Mechanics|first1=Joseph|last1=Spurk|first2=Nuri|last2=Aksel|publisher=Springer|year=2008|isbn=9783540735366|page=174|url=https://books.google.com/books?id=7_FrhazRTgsC&pg=PA174}}.</ref> (berbagi poros pusat yang sama). |
||
==Referensi== |
==Referensi== |
||
Revisi terkini sejak 6 Desember 2021 02.05

Dalam geometri, dua objek atau lebih dikatakan sebagai konsentris, koaksal, atau koaksial saat mereka berbagi pusat atau poros yang sama. Lingkaran,[1] poligon biasa[2] dan polihedra biasa,[3] dan bola[4] dapat menjadi kosentris satu sama lain (berbagi titik pusat yang sama), karena bersifat silinder[5] (berbagi poros pusat yang sama).
Referensi
[sunting | sunting sumber]- ^ Alexander, Daniel C.; Koeberlein, Geralyn M. (2009), Elementary Geometry for College Students, Cengage Learning, hlm. 279, ISBN 9781111788599.
- ^ Hardy, Godfrey Harold (1908), A Course of Pure Mathematics, The University Press, hlm. 107.
- ^ Gillard, Robert D. (1987), Comprehensive Coordination Chemistry: Theory & background, Pergamon Press, hlm. 137, 139, ISBN 9780080262321.
- ^ Kesalahan pengutipan: Tag
<ref>tidak sah; tidak ditemukan teks untuk ref bernamaapostol - ^ Spurk, Joseph; Aksel, Nuri (2008), Fluid Mechanics, Springer, hlm. 174, ISBN 9783540735366.
Pranala luar
[sunting | sunting sumber]- Geometry: Concentric circles demonstration With interactive animation
