Teorema Rolle

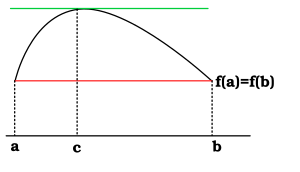
Dalam kalkulus, Teorema Rolle pada dasarnya menyatakan fungsi diferensiabel dan kontinu, yang memiliki nilai sama pada dua titik, mestilah memiliki titik stasioner yang terletak di antara kedua titik tersebut. Pada titik stasioner ini, gradien garis singgung terhadap fungsi tersebut sama dengan nol.

Versi standar

Bila sebuah fungsi riil f kontinu pada selang tertutup [a, b], terdiferensialkan pada selang terbuka (a, b), dan ƒ(a) = ƒ(b), maka ada bilangan c dalam selang terbuka (a, b) sedemikian sehingga

$f'(c)=0.\,$

Versi Teorema Rolle ini digunakan untuk membuktikan teorema nilai purata, yang merupakan kasus umum daripada teorema Rolle.

Generalisasi

Contoh berikut mengilustrasikan generalisasi daripada teorema Rolle:

Perhatikan fungsi riil, kontinu dalam selang tertutup [a, b] dengan f(a) = f(b). Bila untuk setiap x dalam selang terbuka (a,b) limit kanan

$f'(x+):=\lim _{h\to 0^{+}}{\frac {f(x+h)-f(x)}{h}}$

dan limit kiri

$f'(x-):=\lim _{h\to 0^{-}}{\frac {f(x+h)-f(x)}{h}}$

ada pada garis bilangan riil yang diperluas [−∞,∞], maka ada suatu bilangan c pada selang terbuka (a,b) sehingga salah satu dari dua limit

$f'(c+)\quad {\text{and}}\quad f'(c-)$

adalah ≥ 0 dan yang lainnya adalah ≤ 0 (pada garis bilangan riil yang diperluas). Bila limit kiri dan kanan sama untuk setiap x, maka limit ini sama pada khususnya untuk c. Jadi turunan f ada pada c dan sama dengan nol.

Komentar

1. Bila f adalah cekung atau cembung, maka turunan kiri atau kanan ada pada setiap titik dalam, sehingga kedua limit di atas ada dan merupakan bilangan riil
2. Versi yang digeneralisasi ini cukup untuk membuktikan kecekungan fungsi bila salah satu turunan searah naik monoton:

$f'(x-)\leq f'(x+)\leq f'(y-),\qquad x<y.$

Pranala luar

• (Inggris)Teorema Rolle dan Teorema Nilai Rata-rata pada cut-the-knot