Teorema Taylor

Fungsi eksponensial $y=e^{x}$ (garis merah kontinu) dan polinomial Taylor orde empat di sekitar titik asal (garis hijau putus-putus)

Dalam kalkulus, teorema Taylor memberikan barisan pendekatan sebuah fungsi yang diferensiabel pada sebuah titik menggunakan suku banyak (polinomial). Koefisien polinomial tersebut hanya tergantung pada turunan fungsi pada titik yang bersangkutan. Teorema ini juga memberikan estimasi besarnya galat dari pendekatan itu. Teorema ini mendapat nama dari matematikawan Brook Taylor, yang menyatakannya pada tahun 1712, meskipun hasilnya sudah ditemukan pertama kali tahun 1671 oleh James Gregory

Teorema Taylor dalam satu variabel

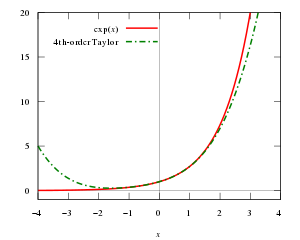
Teorema Taylor menyatakan sembarang fungsi mulus dapat dihampiri dengan polinomial. Contoh sederhana penerapan teorema Taylor adalah hampiran fungsi eksponensial e^x di dekat x = 0:

${\textrm {e}}^{x}\approx 1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots +{\frac {x^{n}}{n!}}.$

Hampiran ini dinamakan hampiran Taylor orde ke-n' terhadap e^x karena menghampiri nilai fungsi eksponensial menggunakan polinomial derajat n. Hampiran ini hanya berlaku untuk x mendekati nol, dan bila x bergerak menjauhi nol, hampiran ini menjadi semakin buruk. Kualitas hampiran dinyatakan oleh suku sisa:

$R_{n}(x)={\textrm {e}}^{x}-\left(1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots +{\frac {x^{n}}{n!}}\right).$

Lebih umum lagi, teorema Taylor berlaku untuk setiap fungsi yang dapat diturunkan ƒ, dengan hampiran untuk x di dekat titik a, dalam bentuk:

$f(x)\approx f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\dots {\frac {f^{(n)}(a)}{n!}}(x-a)^{n}.$

Suku sisa adalah perbedaan antara fungsi dan polinomial hampirannya:

$R_{n}(x)=f(x)-\left(f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\dots {\frac {f^{(n)}(a)}{n!}}(x-a)^{n}\right).$

Meskipun rumus eksplisit untuk suku sisa ini jarang digunakan, teorema Taylor juga memberikan estimasi nilai sisanya. Dengan kata lain, untuk x cukup dekat terhadap a, suku sisa haruslah cukup kecil. Teorema Taylor memberikan informasi persis seberapa kecil suku sisa tersebut.

Pernyataan

Pernyataan cermat teorema ini adalah sebagai berikut: bila n ≥ 0 adalah bilangan bulat dan f adalah fungsi yang terturunkan kontinu pada selang tertutup [a, x] dan terturunkan n + 1 kali pada selang terbuka (a, x), maka

$f(x)=f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f^{(2)}(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}+R_{n}(x).$

Di sini n! melambangkan n faktorial dan R_n(x) adalah suku sisa, melambangkan beda antara polinomial Taylor derajat-n terhadap fungsi asli. Suku sisa R_n(x) tergantung pada x, dan kecil bila x cukup dekat terhadap a. Ada beberapa pernyataan untuk suku sisa ini.

Bentuk Lagrange dari suku sisa menyatakan bahwa terdapat bilangan ξ antara a dan x sedemikian sehingga

$R_{n}(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}(x-a)^{n+1}.$

Ini mengungkapkan teorema Taylor sebagai perampatan teorema nilai rata-rata. Sebenarnya, teorema nilai rata-rata digunakan untuk membuktikan teorema Taylor dengan suku sisa bentuk Lagrange.

Bentuk Cauchy suku sisa menyatakan bahwa terdapat bilangan ξ antara a dan x sehingga

$R_{n}(x)={\frac {f^{(n+1)}(\xi )}{n!}}(x-\xi )^{n}(x-a).$

Secara umum, bila G(t) adalah fungsi kontinu pada selang tertutup [a,x], yang terturunkan dengan turunan tidak nol pada (a,x), maka ada suatu bilangan ξ antara a dan x sehingga

$R_{n}(x)={\frac {f^{(n+1)}(\xi )}{n!}}(x-\xi )^{n}\cdot {\frac {G(x)-G(a)}{G'(\xi )}}.$

Ini mengungkapkan teorema Taylor sebagai generalisasi teorema nilai rata-rata Cauchy.

Bentuk di atas terbatas pada fungsi riil. Namun bentuk integral dari suku sisa juga berlaku untuk fungsi kompleks, yaitu:

$R_{n}(x)=\int _{a}^{x}{\frac {f^{(n+1)}(t)}{n!}}(x-t)^{n}\,dt,$

dengan syarat, seperti yang biasa ditemui, f_n kontinu mutlak dalam [a, x]. Ini menunjukkan teorema ini sebagai perampatan teorema dasar kalkulus.

Secara umum, suatu fungsi tidak perlu sama dengan deret Taylor-nya, karena mungkin saja deret Taylor tersebut tidak konvergen, atau konvergen menuju fungsi yang berbeda. Namun, untuk banyak fungsi f(x), kita dapat menunjukkan bahwa suku sisa R_n mendekati nol saat n mendekati ∞. Fungsi-fungsi tersebut dapat dinyatakan sebagai deret Taylor pada persekitaran titik a, dan disebut sebagai fungsi analitik.

Pranala luar

• (Inggris)Trigonometric Taylor Expansion Applet demonstrasi interaktif
• (Inggris)Taylor Series Revisited pada Holistic Numerical Methods Institute