Pengguna:Dedhert.Jr/Uji halaman 17
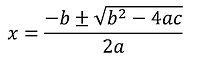
Dalam aljabar elementer, rumus kuadrat adalah sebuah rumus yang mencari sebuah variabel yang tidak diketahui pada persamaan kuadrat.[1] Terkadang, rumus ini disebut juga sebagai rumus ABC karena terkandung tiga variabel pada persamaan tersebut, yakni , , dan ,[2] atau rumus kecap, yang merujuk ke salah satu kecap terkenal di Indonesia, yaitu kecap ABC.[3]
Ringkasan

Bentuk umum persamaan kuadrat dapat ditulis sebagai
- ,
dimana adalah variabel yang tidak diketahui, dan adalah koefisien real (dengan ), memberikan solusi :
- .
Karena adanya tanda plus dan minus, rumus tersebut mempunyai dua solusi, yaitu:
- dan .
Penurunan
Berbagai bukti dan penurunan terhadap rumus kuadrat dapat dilakukan dengan berbagai cara, seperti menyelesaikan dalam bentuk kuadrat sempurna, substitusi, identitas aljabar, dan Lagrange resolvent.

Bentuk kuadrat sempurna
Diberikan persamaan , dengan membagi kedua ruas dengan akan memperoleh . Selanjutnya kurangi kedua ruas dengan .
- .
Pada ruas kiri, kita dapat mengubahnya menjadi bentuk kuadrat dengan menambahkan pada kedua ruas.
- .
Pada ruas kanan, penyebutnya disamakan. Kedua ruas diakarkuadratkan dan dikurangi dengan sehingga kita memperoleh rumus kuadrat.
Melalui teknik yang serupa, terdapat metode sederhana dalam menurunkan rumus ini,[4] yang ditemukan di India sekitar tahun 1025.[5] Metode ini tidak memerlukan bentuk pecahan (termasuk yang diakarkuadratkan) hingga setelah langkah ketiga.
Substitusi
Identitas aljabar
Lagrange resolvent
Rujukan
- ^ M.Pd, Sri Jumini, S. Pd (2017-11-20). Buku Ajar Matematika Dasar Untuk Perguruan Tinggi. Penerbit Mangku Bumi. hlm. 36. ISBN 978-602-52256-2-8.
- ^ "Rumus ABC - Pengertian, Soal, Pembahasan | dosenpintar.com". dosenpintar.com. Diakses tanggal 2022-02-07.
- ^ Mauhibah, Al Jupri, Rohma (2014-01-01). Trik Cerdas Paling Cadas Pintar Matematika SMA. PandaMedia. hlm. 64. ISBN 978-979-780-658-3.
- ^ Hoehn, Larry (1975). "A More Elegant Method of Deriving the Quadratic Formula". The Mathematics Teacher. 68 (5): 442–443. doi:10.5951/MT.68.5.0442.
- ^ Smith, David E. (1958). History of Mathematics, Vol. II. Dover Publications. hlm. 446. ISBN 0486204308.
Daftar pustaka
- CCSS HSA-REI.B.4 Completing the Square to Solve Quadratic Equations: Aligns to CCSS HSA-REI.B.4: Solve quadratic equations in one variable. (dalam bahasa Inggris). Lorenz Educational Press. 2014-01-01. hlm. 51. ISBN 978-0-7877-1056-9.
- Hanna, Gila; Jahnke, Hans Niels; Pulte, Helmut (2009-12-04). Explanation and Proof in Mathematics: Philosophical and Educational Perspectives (dalam bahasa Inggris). Springer Science & Business Media. hlm. 91. ISBN 978-1-4419-0576-5.
- Varberg, Dale. Kalkulus, Edisi Kesembilan, Jilid 1. Penerbit Erlangga. hlm. 14. ISBN 0-13-1429-24-8.























