Teorema Rolle

Dalam kalkulus, Teorema Rolle pada dasarnya menyatakan fungsi diferensiabel dan kontinu, yang memiliki nilai sama pada dua titik, mestilah memiliki titik stasioner yang terletak di antara kedua titik tersebut. Pada titik stasioner ini, gradien garis singgung terhadap fungsi tersebut sama dengan nol.

Versi standar

Bila sebuah fungsi riil f kontinu pada selang tertutup [a, b], terdiferensialkan pada selang terbuka (a, b), dan ƒ(a) = ƒ(b), maka ada bilangan c dalam selang terbuka (a, b) sedemikian sehingga

f'(c)=0.\,

Versi Teorema Rolle ini digunakan untuk membuktikan teorema nilai purata, yang merupakan kasus umum daripada teorema Rolle.

Generalisasi

Contoh berikut mengilustrasikan generalisasi daripada teorema Rolle:

Perhatikan fungsi riil, kontinu dalam selang tertutup [a, b] dengan f(a) = f(b). Bila untuk setiap x dalam selang terbuka (a,b) limit kanan

f'(x+):=\lim _{h\to 0^{+}}{\frac {f(x+h)-f(x)}{h}}

dan limit kiri

f'(x-):=\lim _{h\to 0^{-}}{\frac {f(x+h)-f(x)}{h}}

ada pada garis bilangan riil yang diperluas [−∞,∞], maka ada suatu bilangan c pada selang terbuka (a,b) sehingga salah satu dari dua limit

f'(c+)\quad {\text{dan}}\quad f'(c-)

adalah ≥ 0 dan yang lainnya adalah ≤ 0 (pada garis bilangan riil yang diperluas). Bila limit kiri dan kanan sama untuk setiap x, maka limit ini sama pada khususnya untuk c. Jadi turunan f ada pada c dan sama dengan nol.

Komentar

Bila f adalah cekung atau cembung, maka turunan kiri atau kanan ada pada setiap titik dalam, sehingga kedua limit di atas ada dan merupakan bilangan riil
Versi yang digeneralisasi ini cukup untuk membuktikan kecekungan fungsi bila salah satu turunan searah naik monoton:

^[1]

f'(x-)\leq f'(x+)\leq f'(y-),\qquad x<y.

Contoh

Contoh pertama

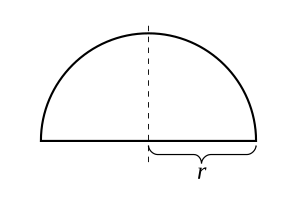
Sebuah **setengah lingkaran** dengan radius $r$ .

Untuk radius angka $r > 0$ , pertimbangkan dengan fungsi:

f(x)={\sqrt {r^{2}-x^{2}}},\quad x\in [-r,r].

grafik adalah setengah lingkaran atas yang berpusat pada titik asal. Fungsi ini berlanjut pada interval tertutup $[- r, r]$ dan dibedakan dalam interval terbuka $(- r, r)$ , tetapi tidak dapat dibedakan di titik akhir $- r$ dan $r$ . Setelah mencari $f (- r) = f (r)$ , Teorema Rolle berlaku, dan memang, ada titik darimana turunan $f$ adalah nilai nol. Perhatikan bahwa teorema berlaku bahkan ketika fungsi tidak dapat dibedakan di titik akhir karena hanya memerlukan fungsi tersebut untuk dapat dibedakan dalam interval terbuka.

Contoh kedua

Jika diferensiabilitas gagal pada titik interior interval, kesimpulan teorema Rolle mungkin tidak berlaku. Pertimbangkan fungsi nilai absolut:

f(x)=|x|,\qquad x\in [-1,1].

Kemudian $f (-1) = f (1)$ , tapi tidak ada nilai $c$ antara −1 dan 1 pada nilai $f'(c)$ adalah nol. Hal tersebut karena fungsi itu, meskipun kontinu, tidak dapat dibedakan pada nilai $x = 0$ . Perhatikan bahwa turunan dari $f$ mengubah tandanya pada $x = 0$ , tetapi tanpa mencapai nilai 0. Teorema tidak dapat diterapkan pada fungsi ini karena tidak memenuhi syarat bahwa fungsi harus dapat dibedakan untuk setiap nilai $x$ dalam interval terbuka. Namun, ketika persyaratan diferensiabilitas dihilangkan dari teorema Rolle, $f$ akan tetap memiliki angka kritis dalam interval terbuka $(a, b)$ , tetapi mungkin tidak menghasilkan garis singgung horizontal (seperti dalam kasus nilai absolut yang ditunjukkan dalam grafik).

Pembuktian

Di sini akan dibuktikan teorema yang sudah digeneralisasi.

Gagasan dasarnya adalah bahwa bila f(a) = f(b), maka f mestilah mencapai maksimum atau minimum di suatu titik antara a dan b. Sebutlah titik ini c. Fungsi tersebut juga harus berubah dari naik menjadi turun (atau sebaliknya) pada c. Khususnya, bila turunannya ada, nilainya mestilah nol pada c.

Dari asumsi, diketahui f kontinu pada [a,b] dan menurut teorema nilai ekstrem mencapai baik maksimum maupun minimumnya dalam [a,b]. Bila keduanya dicapai pada titik batas [a,b] maka f adalah fungsi konstan pada [a,b] dan turunannya adalah nol pada setiap titik pada (a,b).

Misalkan bila maksimum diperoleh pada titik dalam c pada selang (a, b) (argumen untuk nilai minimum mirip, perhatikan −f ). Kita akan memeriksa limit kanan dan kiri secara terpisah.

Untuk h riil sedemikian sehingga c + h adalah dalam [a,b], nilai f(c + h) lebih kecil atau sama dengan f(c) karena f mencapai maksimumnya pada c. Karena itu, untuk setiap h > 0,