Modus (statistika)
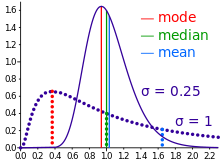
Modus adalah nilai yang paling sering muncul dalam suatu data statistika.[1] Modus juga merupakan nilai mayoritas atau nilai dengan frekuensi paling tinggi. Modus dapat digunakan untuk menentukan sampel dari suatu populasi dalam statistika. Perhitungan modus dapat diterapkan pada data numerik maupun data kategoris, contohnya dalam menentukan data dari warna paling banyak disukai siswa dan mayoritas nilai ulangan sebuah mata pelajaran yang diperoleh oleh siswa dalam suatu kelas.
Modus digunakan untuk ukuran pemusatan data seperti halnya mean dan median. Modus berisikan informasi penting dalam suatu variabel atau populasi acak.
Jenis-jenis modus
Unimodal
Suatu data yang memiliki satu nilai modus disebut unimodal.[2] Data yang memiliki satu modus dapat diilustrasikan pada kondisi berikut:
Nilai ulangan matematika dari suatu kelas adalah sebagai berikut:
75, 60, 55, 70, 50, 60, 65, 60, 52, 60, 85, 65, 75, 40, 80, 45, 90
Dari data tersebut diperoleh nilai modus yakni 60 karena diperoleh oleh empat siswa, lebih banyak dari nilai lainnya. Data tersebut hanya memiliki satu nilai modus, yakni 60, sehingga disebut distribusi unimodal.
Bimodal
Suatu data yang memiliki dua nilai modus disebut bimodal.[3] Contohnya adalah sebagai berikut:
Nilai bahasa Inggris dari suatu kelas adalah sebagai berikut:
70, 60, 55, 75, 85, 60, 50, 85, 80, 75, 70, 75, 80, 90, 50, 85, 95

Berdasarkan data tersebut, terdapat dua nilai modus, yaitu nilai 75 dan 85 yang diperoleh oleh masing-masing tiga siswa sama banyak, sehingga data tersebut disebut dengan distribusi bimodal. Data distribusi bimodal memiliki dua puncak nilai dengan frekuensi yang sama.
Multimodal
Data yang di dalamnya terdapat lebih dari dua nilai modus disebut multimodal.[3]
Berikut adalah ilustrasi untuk memahami data dengan nilai modus lebih dari dua:
Nilai pelajaran bahasa Indonesia dalam suatu kelas adalah sebagai berikut:

70, 65, 60, 70, 70, 60, 85, 50, 80, 75, 55, 75, 85, 80, 75, 50, 85, 90, 60, 95, 90, 70, 75, 85, 45, 40, 60
Dari data tersebut, terdapat tiga nilai terbanyak yang diperoleh siswa, yakni nilai 70, 75, dan 85 yang masing-masing didapatkan oleh 4 siswa.
Modus data tunggal
Modus pada data tunggal dapat ditentukan dengan mendaftar data tersebut dalam sebuah tabel. Berikut adalah ilustrasi untuk menentukan nilai modus.
Nilai matematika yang diperoleh oleh siswa kelas IX A adalah sebagai berikut:
40, 60, 50, 40, 60, 45, 70, 40, 75, 65, 70, 80, 75, 85, 60, 70, 80, 90, 35, 70, 75, 85, 90, 45, 55, 70, 40, 35, 60, 75, 80, 70, 60, 65, 70, 85
Untuk menentukan modus dari data tersebut langkah yang harus dilakukan adalah membuat sebuah tabel dengan menghitung frekuensi dari nilai-nilai tersebut.
Modus data berkelompok
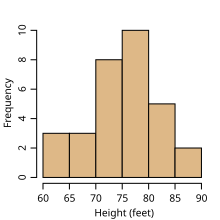
Modus data berkelompok dapat ditentukan dengan menggunakan modus besar dan rumus. Modus besar merupakan titik tengah interval kelas yang memiliki frekuensi terbanyak. Kelas interval yang memiliki frekuensi terbanyak disebut kelas modus.[4]
Modus pada data berkelompok juga dapat ditentukan dengan menggunakan rumus.
L = tepi bawah kelas modus
d1 = selisih frekuensi kelas modus dengan frekuensi kelas sebelumnya
d2 = selisih frekuensi kelas modus dengan frekuensi kelas setelahnya
i = interval kelas = lebar kelas[4]
Referensi
- ^ Agus, Nuniek Avianti (2007). Mudah Belajar Matematika. Jakarta: Pusat Perbukuan Departermen Pendidikan Nasional. hlm. 138. ISBN 9794628182.
- ^ Stephanie (2015-07-27). "Multimodal Distribution Definition and Examples". Statistics How To (dalam bahasa Inggris). Diakses tanggal 2020-08-25.
- ^ a b "1.3.3.14.4. Histogram Interpretation: Symmetric and Bimodal". www.itl.nist.gov. Diakses tanggal 2020-08-25.
- ^ a b Pd, Yuliansyah, S. Pd M. (2020-07-04). BUKU PENUNJANG BAHAN AJAR MATEMATIKA SMK KELAS XII. CV SUKA ILMU.

