Lompat ke isi

Metaheuristik

Dari Wikipedia bahasa Indonesia, ensiklopedia bebas

Dalam bidang Ilmu Komputer dan Optimasi Matematika, metaheuristik (bahasa Inggris: metaheuristic) didefinisikan sebagai suatu prosedur tingkat tinggi atau pendekatan heuristik yang dirancang agar dapat menemukan, menghasilkan, mengoptimalkan, atau memilih suatu heuristik (algoritma pencarian parsial) yang dapat memberikan solusi yang memadai terhadap suatu permasalahan optimasi atau pemelajaran mesin. Secara khusus, metaheuristik digunakan pada permasalahan yang memiliki keterbatasan informasi atau ketidaklengkapan data, atau dengan kapasitas (sumber daya) komputasi yang terbatas.[1][2] Metaheuristik memungkinkan pengambilan sampel dari subkumpulan solusi yang dengannya memungkinkan calon-calon solusi tersebut dapat dievaluasi secara efisien. Metaheuristik juga mungkin dapat membuat asumsi dengan jumlah yang relatif sedikit terkait masalah optimasi yang sedang dipecahkan, sehingga ia dapat digunakan untuk berbagai jenis permasalahan.[3]

Jika dibandingkan dengan algoritma optimasi dan algoritma iteratif, metaheuristik tidak dapat menjamin ditemukannya solusi optimal yang berlaku secara global pada beberapa jenis permasalahan.[3] Hal ini disebabkan oleh banyaknya metode metaheuristik yang menerapkan optimasi stokastik, sehingga solusi yang ditemukan bergantung pada himpunan variabel acak yang dihasilkan.[1] Sebagai contoh, pada kasus optimasi kombinatorial, suatu algoritma mencari solusi di dalam himpunan besar yang berisi kandidat-kandidat solusi. Dalam kasus ini, metaheuristik sering kali dapat menemukan solusi yang bagus dengan usaha komputasi yang lebih sedikit, jika dibandingkan dengan algoritma optimasi, metode iteratif, atau heuristik sederhana.[3] Oleh karena itu, pendekatan metaheuristik ini bermanfaat dalam masalah optimasi [1] dan sudah banyak buku dan makalah survei telah diterbitkan mengenai hal tersebut.[1][3] Terkait dengan awal penemuannya, studi literatur terkait optimasi metaheuristik, [4] mengemukakan bahwa Fred Glover-lah yang awalnya menemukan kata “metaheuristik” pertama kali. [5]

Kebanyakan literatur terkait metaheuristik bersifat eksperimental. Dengan cara mendeskripsikan hasil empiris berdasarkan eksperimen komputer dengan algoritma yang diteliti. Namun, terdapat juga beberapa hasil teoretis formal terkait hal ini yang sering kali mengenai konvergensi dan sejauh mana kemungkinan algoritma tersebut mampu menemukan optimal global.[3] Banyak metode metaheuristik telah diterbitkan dengan klaim kebaruan (novelty) dan kemanjuran praktis. Meskipun bidang ini banyak menyajikan penelitian dengan kualitas tinggi, tetapi banyak juga publikasi yang berkualitas buruk. Hal ini disebabkan karena ketidakjelasan, kurangnya elaborasi konseptual, eksperimen yang buruk, dan minimnya pengetahuan terhadap literatur sebelumnya. [6]

Sifat-sifat

Berikut adalah sifat-sifat yang menjadi ciri sebagian besar metaheuristik:[3]

  • Metaheuristik adalah strategi yang memandu proses pencarian.
  • Metaheuristik bertujuan untuk mengeksplorasi ruang pencarian secara efisien untuk menemukan solusi yang mendekati optimal.
  • Teknik yang membentuk algoritma metaheuristik berkisar antara prosedur pencarian lokal yang sederhana hingga proses pemelajaran yang kompleks.
  • Algoritma metaheuristik bersifat perkiraan dan biasanya bersifat non-deterministik.
  • Metaheuristik tidak spesifik terhadap suatu masalah.

Klasifikasi

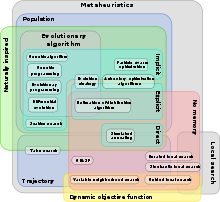
Diagram Euler tentang klasifikasi metaheuristik yang berbeda. [7]

Terdapat berbagai jenis metaheuristik [1] dan sejumlah karakteristik yang dapat digunakan untuk mengklasifikasikannya.[3]

Pencarian lokal vs. pencarian global

Pendekatan pertama untuk mengklasifikasikan algoritma metaheuristik adalah dari sisi strategi pencarian yang digunakan.[3] Salah satu jenis strategi pencarian adalah perbaikan terhadap algoritma pencarian lokal yang bersifat sederhana. Salah satu algoritma pencarian lokal yang terkenal adalah metode hill climbing yang digunakan untuk mencari solusi optimum lokal. Namun, algoritma tersebut tidak dapat menjamin ditemukannya solusi optimal global.

Banyak ide-ide metode metaheuristik yang diajukan untuk meningkatkan heuristik pencarian lokal guna menemukan solusi yang lebih baik. Metaheuristik tersebut mencakup simulated annealing, tabu search, iterated local search, variable neighborhood search, dan GRASP.[3] Metide-metdode metaheuristik ini dapat diklasifikasikan sebagai metaheuristik berbasis pencarian lokal atau pencarian global.

Metaheuristik pencarian global lainnya yang tidak berbasis pencarian lokal biasanya adalah metaheuristik berbasis populasi . Metaheuristik tersebut meliputi optimasi koloni semut, komputasi evolusioner seperti algoritma genetika atau evolution strategy, particle swarm optimization, rider optimization algorithm [8] dan algoritma bacterial foraging. [9]

Solusi tunggal vs. berbasis populasi

Metode klasifikasi lainnya adalah pencarian solusi tunggal atau berbasis populasi.[3] Pendekatan solusi tunggal fokus terhadap modifikasi dan meningkatkan kualitas kandidat solusi tunggal. Pendekatan ini mencakup simulated annnealing, iterated local search, variable neighborhood search, dan guided local search. Sedangkan untuk pendekatan berbasis populasi, metode ini mempertahankan dan meningkatkan banyak kandidat solusi, sering kali menggunakan karakteristik populasi untuk memandu proses pencarian, metaheuristik yang menggunakan pendekatan ini mencakup komputasi evolusioner dan particle swarm optimization. Kategori metaheuristik lainnya adalah kecerdasan gerombolan atau swarm intelligence yang merupakan perilaku kolektif dari agen-agen yang terdesentralisasi dan terorganisir sendiri dalam suatu populasi atau gerombolan. Optimasi koloni semut, [10] particle swarm optimization, social cognitive optimization, dan algoritma bacterial foraging [9] adalah contoh dari kategori ini.

Algoritma hibridisasi dan memetika

Metaheuristik hibrid adalah metode yang menggabungkan metaheuristik dengan pendekatan optimasi lainnya, seperti algoritma pemrograman matematika, constraint programming, dan pembelajaran mesin. Kedua komponen metaheuristik hibrid dapat berjalan secara bersamaan dan dapat bertukar informasi untuk memandu proses pencarian.

Di sisi lain, algoritma Memetika adalah metode metaheuristik yang merepresentasikan sinergi pendekatan evolusioner atau pendekatan berbasis populasi dengan pembelajaran individu yang terpisah atau prosedur perbaikan lokal untuk pencarian solusi di suatu masalah. Contoh algoritma memetik adalah penggunaan algoritma pencarian lokal sebagai pengganti atau tambahan operator mutasi dasar di dalam algoritma evolusioner.

Metaheuristik paralel

Metaheuristik paralel adalah metode metaheuristik yang menggunakan teknik-teknik pemrograman paralel untuk menjalankan beberapa pencarian metaheuristik secara paralel; ini dapat berkisar dari skema terdistribusi sederhana hingga pencarian yang dilakukan secara bersamaan yang berinteraksi untuk meningkatkan solusi secara keseluruhan.

Metaheuristik yang terinspirasi dari alam dan berbasis metafora

Artikel utama: Kecerdasan gerombolan dan Daftar metode metaheuristik berbasis metafora

Bidang penelitian yang sangat aktif di bidang ini adalah desain metaheuristik yang terinspirasi dari alam. Banyak metaheuristik terkini, khususnya algoritma berbasis komputasi evolusioner, terinspirasi oleh sistem alam. Dengan pendekatan ini, alam bertindak sebagai sumber konsep, mekanisme, dan prinsip untuk merancang sistem komputasi buatan untuk menangani masalah komputasi yang kompleks. Metaheuristik yang menggunakan pendekatan ini mencakup simulated annealing, algoritma evolusioner, optimasi koloni semut dan particle swarm optimization. Sejumlah besar metaheuristik yang terinspirasi dari metafora baru-baru ini mulai menarik kritik dari komunitas riset karena menyembunyikan kurangnya kebaruan di balik metafora yang rumit.[6]

Aplikasi

Metaheuristik adalah pendekatan yang digunakan untuk menyelesaikan berbagai jenis masalah optimasi, termasuk masalah yang melibatkan variabel kontinu, variabel bilangan bulat, atau kombinasi keduanya. Dalam konteks optimasi kombinatorial, fokusnya adalah pada pencarian solusi optimal di dalam ruang pencarian yang terdiri dari pilihan diskrit. Sebagai contoh, kita dapat mempertimbangkan permasalahan penjual keliling, di mana kita mencari rute terbaik untuk mengunjungi sejumlah lokasi dengan efisiensi maksimal. Masalah ini menunjukkan karakteristik di mana jumlah kemungkinan solusi tumbuh secara eksponensial seiring dengan bertambahnya ukuran masalah. Dengan kata lain, mencari solusi optimal dengan memeriksa setiap kemungkinan secara menyeluruh menjadi tidak mungkin atau tidak efisien seiring pertambahan kompleksitas masalah. Selain itu, masalah kombinatorial multidimensi, termasuk sebagian besar masalah desain di bidang teknik [11] [12] [13] di mana mencari bentuk atau perilaku optimal melibatkan ruang pencarian yang sangat besar sehinga mengalami kutukan dimensi, yang juga membuatnya tidak layak untuk pencarian mendalam atau metode analitis.

Metaheuristik juga sering digunakan untuk menyelesaikan masalah penjadwalan, di mana salah satu contoh klasiknya adalah penjadwalan job shop. Penjadwalan job shop melibatkan penentuan urutan langkah kerja untuk setiap pekerjaan di stasiun pemrosesan sedemikian rupa sehingga semua pekerjaan diselesaikan tepat waktu dan dalam waktu sesingkat mungkin. [14] [15]Dalam praktiknya, seringkali terdapat pembatasan seperti batasan urutan langkah kerja melalui alur kerja yang telah ditentukan, [16] atau keterbatasan terkait pemanfaatan sumber daya, misalnya, dalam hal penggunaan energi. [17] [18] Metaheuristik populer untuk masalah kombinatorial termasuk algoritma genetika oleh Holland et al., scatter search, dan tabu search oleh Glover.

Penerapan besar lainnya dari metaheuristik terjadi dalam tugas pengoptimalan di ruang pencarian bilangan bulat kontinu atau campuran. Terdapat berbagai aplikasi di bidang optimasi desain [19] [20] [21] atau berbagai tugas teknik. [22] [23] [24] Salah satu contoh yang mencakup kedua aspek ini adalah perencanaan jalur gerak yang optimal untuk robot industri. [25] [26]

Kerangka Optimasi Metaheuristik

Kerangka Optimasi Metaheuristik atau Metaheuristic Optimization Frameworks (MOF) dapat didefinisikan sebagai ''seperangkat perangkat lunak yang menyediakan implementasi yang benar dan dapat digunakan kembali dari serangkaian metaheuristik, dan mekanisme-mekanisme dasar untuk mempercepat implementasi heuristik bawahan (mungkin termasuk pengkodean solusi dan operator teknik tertentu), yang diperlukan untuk menyelesaikan suatu masalah tertentu dengan menggunakan teknik yang telah disediakan''.

Terdapat banyak kandidat alat optimzasi yang dapat dianggap sebagai MOF dengan berbagai macam fitur: Comet, EvA2, evolvica, Evolutionary::Algorithm, GAPlayground, jaga, JCLEC, JGAP, jMetal, n-genes, Open Beagle, Opt4j, ParadisEO/EO, Pisa, Watchmaker, FOM, Hypercube, HotFrame, Templar, EasyLocal, iOpt, OptQuest, JDEAL, Optimization Algorithm Toolkit, HeuristicLab, MAFRA, Localizer, GALIB, DREAM, Discropt, MALLBA, MAGMA, Metaheuristics.jl, UOF, dan OptaPlanner.

Kontribusi

Beberapa kontribusi paling signifikan di bidang metaheuristik mencakup pengembangan berbagai algoritma dan pendekatan yang telah memberikan dampak besar pada penyelesaian masalah optimasi yang kompleks. Berikut adalah beberapa kontribusi signifikan di bidang ini:

Lihat juga

Referensi

  1. ^ a b c d e Bianchi, Leonora; Marco Dorigo; Luca Maria Gambardella; Walter J. Gutjahr (2009). "A survey on metaheuristics for stochastic combinatorial optimization" (PDF). Natural Computing. 8 (2): 239–287. doi:10.1007/s11047-008-9098-4. 
  2. ^ R. Balamurugan; A.M. Natarajan; K. Premalatha (2015). "Stellar-Mass Black Hole Optimization for Biclustering Microarray Gene Expression Data". Applied Artificial Intelligence. 29 (4): 353–381. doi:10.1080/08839514.2015.1016391 alt=Dapat diakses gratis. 
  3. ^ a b c d e f g h i j Blum, C.; Roli, A. (2003). "Metaheuristics in combinatorial optimization: Overview and conceptual comparison". 35 (3). ACM Computing Surveys: 268–308. 
  4. ^ X. S. Yang, Metaheuristic optimization, Scholarpedia, 6(8):11472 (2011).
  5. ^ Glover F., (1986).
  6. ^ a b Sörensen, Kenneth (2015). "Metaheuristics—the metaphor exposed" (PDF). International Transactions in Operational Research. 22: 3–18. doi:10.1111/itor.12001. Diarsipkan dari versi asli (PDF) tanggal 2013-11-02. 
  7. ^ Classification of metaheuristics
  8. ^ D, Binu (2019). "RideNN: A New Rider Optimization Algorithm-Based Neural Network for Fault Diagnosis in Analog Circuits". IEEE Transactions on Instrumentation and Measurement. 68 (1): 2–26. Bibcode:2019ITIM...68....2B. doi:10.1109/TIM.2018.2836058. 
  9. ^ a b Pang, Shinsiong; Chen, Mu-Chen (2023-06-01). "Optimize railway crew scheduling by using modified bacterial foraging algorithm". Computers & Industrial Engineering (dalam bahasa Inggris). 180: 109218. doi:10.1016/j.cie.2023.109218. ISSN 0360-8352. 
  10. ^ a b M. Dorigo, Optimization, Learning and Natural Algorithms, PhD thesis, Politecnico di Milano, Italie, 1992.
  11. ^ Tomoiagă B, Chindriş M, Sumper A, Sudria-Andreu A, Villafafila-Robles R. Pareto Optimal Reconfiguration of Power Distribution Systems Using a Genetic Algorithm Based on NSGA-II.
  12. ^ Ganesan, T.; Elamvazuthi, I.; Ku Shaari, Ku Zilati; Vasant, P. (2013-03-01). "Swarm intelligence and gravitational search algorithm for multi-objective optimization of synthesis gas production". Applied Energy. 103: 368–374. doi:10.1016/j.apenergy.2012.09.059. 
  13. ^ Ganesan, T.; Elamvazuthi, I.; Vasant, P. (2011-11-01). "Evolutionary normal-boundary intersection (ENBI) method for multi-objective optimization of green sand mould system". 2011 IEEE International Conference on Control System, Computing and Engineering. hlm. 86–91. doi:10.1109/ICCSCE.2011.6190501. ISBN 978-1-4577-1642-3. 
  14. ^ Jarboui, Bassem; Siarry, Patrick; Teghem, Jacques, ed. (2013). Metaheuristics for production scheduling. Automation - control and industrial engineering series. London: ISTE. ISBN 978-1-84821-497-2. 
  15. ^ Xhafa, Fatos; Abraham, Ajith, ed. (2008). Metaheuristics for Scheduling in Industrial and Manufacturing Applications. Studies in Computational Intelligence (dalam bahasa Inggris). 128. Berlin, Heidelberg: Springer Berlin Heidelberg. doi:10.1007/978-3-540-78985-7. ISBN 978-3-540-78984-0. 
  16. ^ Jakob, Wilfried; Strack, Sylvia; Quinte, Alexander; Bengel, Günther; Stucky, Karl-Uwe; Süß, Wolfgang (2013-04-22). "Fast Rescheduling of Multiple Workflows to Constrained Heterogeneous Resources Using Multi-Criteria Memetic Computing". Algorithms (dalam bahasa Inggris). 6 (2): 245–277. doi:10.3390/a6020245. ISSN 1999-4893. 
  17. ^ Kizilay, Damla; Tasgetiren, M. Fatih; Pan, Quan-Ke; Süer, Gürsel (2019). "An Ensemble of Meta-Heuristics for the Energy-Efficient Blocking Flowshop Scheduling Problem". Procedia Manufacturing (dalam bahasa Inggris). 39: 1177–1184. doi:10.1016/j.promfg.2020.01.352. 
  18. ^ Grosch, Benedikt; Weitzel, Timm; Panten, Niklas; Abele, Eberhard (2019). "A metaheuristic for energy adaptive production scheduling with multiple energy carriers and its implementation in a real production system". Procedia CIRP (dalam bahasa Inggris). 80: 203–208. doi:10.1016/j.procir.2019.01.043. 
  19. ^ Gupta, Shubham; Abderazek, Hammoudi; Yıldız, Betül Sultan; Yildiz, Ali Riza; Mirjalili, Seyedali; Sait, Sadiq M. (2021). "Comparison of metaheuristic optimization algorithms for solving constrained mechanical design optimization problems". Expert Systems with Applications (dalam bahasa Inggris). 183: 115351. doi:10.1016/j.eswa.2021.115351. 
  20. ^ Quinte, Alexander; Jakob, Wilfried; Scherer, Klaus-Peter; Eggert, Horst (2002), Laudon, Matthew, ed., "Optimization of a Micro Actuator Plate Using Evolutionary Algorithms and Simulation Based on Discrete Element Methods", International Conference on Modeling and Simulation of Microsystems: MSM 2002, Cambridge, Mass: Computational Publications: 192–197, ISBN 978-0-9708275-7-9 
  21. ^ Parmee, I. C. (1997), Dasgupta, Dipankar; Michalewicz, Zbigniew, ed., "Strategies for the Integration of Evolutionary/Adaptive Search with the Engineering Design Process", Evolutionary Algorithms in Engineering Applications (dalam bahasa Inggris), Berlin, Heidelberg: Springer: 453–477, doi:10.1007/978-3-662-03423-1_25, ISBN 978-3-642-08282-5, diakses tanggal 2023-07-17 
  22. ^ Valadi, Jayaraman; Siarry, Patrick, ed. (2014). Applications of Metaheuristics in Process Engineering (dalam bahasa Inggris). Cham: Springer International Publishing. doi:10.1007/978-3-319-06508-3. ISBN 978-3-319-06507-6. 
  23. ^ Sanchez, Ernesto; Squillero, Giovanni; Tonda, Alberto (2012). Industrial Applications of Evolutionary Algorithms. Intelligent Systems Reference Library (dalam bahasa Inggris). 34. Berlin, Heidelberg: Springer. doi:10.1007/978-3-642-27467-1. ISBN 978-3-642-27466-4. 
  24. ^ Akan, Taymaz; Anter, Ahmed M.; Etaner-Uyar, A. Şima; Oliva, Diego, ed. (2023). Engineering Applications of Modern Metaheuristics. Studies in Computational Intelligence (dalam bahasa Inggris). 1069. Cham: Springer International Publishing. doi:10.1007/978-3-031-16832-1. ISBN 978-3-031-16831-4. 
  25. ^ Blume, Christian (2000), Cagnoni, Stefano, ed., "Optimized Collision Free Robot Move Statement Generation by the Evolutionary Software GLEAM", Real-World Applications of Evolutionary Computing, Lecture Notes in Computer Science (dalam bahasa Inggris), Berlin, Heidelberg: Springer, 1803: 330–341, doi:10.1007/3-540-45561-2_32, ISBN 978-3-540-67353-8, diakses tanggal 2023-07-17 
  26. ^ Pholdee, Nantiwat; Bureerat, Sujin (2018-12-14), "Multiobjective Trajectory Planning of a 6D Robot based on Multiobjective Meta Heuristic Search", International Conference on Network, Communication and Computing (ICNCC 2018) (dalam bahasa Inggris), ACM: 352–356, doi:10.1145/3301326.3301356, ISBN 978-1-4503-6553-6 
  27. ^ Moscato, P.; Fontanari, J.F. (1990), "Stochastic versus deterministic update in simulated annealing", Physics Letters A, 146 (4): 204–208, Bibcode:1990PhLA..146..204M, doi:10.1016/0375-9601(90)90166-L 
  28. ^ Dueck, G.; Scheuer, T. (1990), "Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing", Journal of Computational Physics, 90 (1): 161–175, Bibcode:1990JCoPh..90..161D, doi:10.1016/0021-9991(90)90201-B, ISSN 0021-9991 

Bacaan lebih lanjut


Tautan eksternal

Templat:Optimization algorithms

Diperoleh dari "https://wiki-indonesia.club/w/index.php?title=Metaheuristik&oldid=25254589"