Fungsi monoton

Gambar 1. Contoh grafik fungsi yang tidak monotonik

Dalam matematika, fungsi monotonik atau fungsi monoton adalah sebuah fungsi antar himpunan terurut yang mengawetkan atau membalikan suatu urutan. Konsep ini pertama kali muncul dalam kalkulus, dan selanjutnya diperumum untuk masalah-masalah di teori urutan.

Gambar 2. Contoh grafik fungsi monotonik tak-menaik.

Gambar 3. Contoh grafik fungsi monotonik tak-menurun.

Dalam kalkulus dan analisis

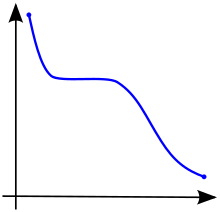
Dalam kalkulus, sebuah fungsi $f$ bernilai real yang terdefinisi pada suatu subset dari himpunan bilangan real, dikatakan monotonik jika fungsi tersebut seluruhnya tak-menaik atau seluruhnya tak-menurun. Sebagai contoh, Gambar 2. menunjukkan grafik fungsi yang turun secara monotonik tidak perlu selalu menurun, cukup tidak pernah meningkat.

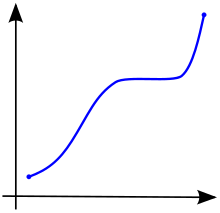
Sebuah fungsi dikatakan monoton naik (juga dikatakan naik secara monotonik, menaik, atau tak-menurun), jika untuk setiap $x$ dan $y$, dengan $x\leq y$, akan berlaku $f\!\left(x\right)\leq f\!\left(y\right)$. Fungsi $f$ yang memenuhi hubungan tersebut dikatakan mengawetkan urutan. Serupa dengan itu, sebuah fungsi dikatakan monoton turun (juga dikatakan turun secara monotonik, menurun, atau tak-menaik) jika $x\leq y$, maka berlaku $f\!\left(x\right)\geq f\!\left(y\right)$. Fungsi monoton membalikkan urutan.

Urutan $\leq$ dalam definisi kemonotonikan dapat diganti dengan urutan tegas (strict order) $<$ untuk menghasilkan definisi yang lebih kuat. Fungsi yang memenuhi definisi ini disebut fungsi menaik tegas (terkadang cukup disebut menaik). Serupa dengan itu, dengan membalik simbol pertidaksamaan, didapatkan konsep yang disebut menurun tegas (terkadang cukup disebut menurun).

Daftar pustaka

• Bartle, Robert G. (1976). The elements of real analysis (edisi ke-second). 
• Grätzer, George (1971). Lattice theory: first concepts and distributive lattices. ISBN 0-7167-0442-0. 
• Pemberton, Malcolm; Rau, Nicholas (2001). Mathematics for economists: an introductory textbook. Manchester University Press. ISBN 0-7190-3341-1. 
• Renardy, Michael; Rogers, Robert C. (2004). An introduction to partial differential equations. Texts in Applied Mathematics 13 (edisi ke-Second). New York: Springer-Verlag. hlm. 356. ISBN 0-387-00444-0. 
• Riesz, Frigyes; Béla Szőkefalvi-Nagy (1990). Functional Analysis. Courier Dover Publications. ISBN 978-0-486-66289-3. 
• Russell, Stuart J.; Norvig, Peter (2010). Artificial Intelligence: A Modern Approach (edisi ke-3rd). Upper Saddle River, New Jersey: Prentice Hall. ISBN 978-0-13-604259-4. 
• Simon, Carl P.; Blume, Lawrence (April 1994). Mathematics for Economists (edisi ke-first). ISBN 978-0-393-95733-4.  (Definition 9.31)

Pranala luar

• Hazewinkel, Michiel, ed. (2001) [1994], "Monotone function", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4 
• Convergence of a Monotonic Sequence Diarsipkan 2023-06-06 di Wayback Machine. by Anik Debnath and Thomas Roxlo (The Harker School), Wolfram Demonstrations Project.
• (Inggris) Weisstein, Eric W. "Monotonic Function". MathWorld.