Mesin Turing

Mesin Turing adalah model komputasi teoretis yang ditemukan oleh Alan Turing, berfungsi sebagai model ideal untuk melakukan perhitungan matematis. Walaupun model ideal ini diperkenalkan sebelum komputer nyata dibangun, model ini tetap diterima kalangan ilmu komputer sebagai model komputer yang sesuai untuk menentukan apakah suatu fungsi dapat selesaikan oleh komputer atau tidak (menentukan computable function). Mesin Turing terkenal dengan ungkapan " Apapun yang bisa dilakukan oleh Mesin Turing pasti bisa dilakukan oleh komputer."

Sebuah mesin turing terdiri atas barisan sel tersusun berupa pita yang dapat bergerak maju mundur, komponen aktif baca/tulis pita yang memiliki status perhitungan serta dapat mengubah/menulisi sel aktif yang ada di pita tadi, dan suatu kumpulan instruksi bagaimana komponen baca/tulis ini harus melakukan modifikasi terhadap sel aktif pada pita, serta bagaimana menggerakkan pita tersebut. Pada setiap langkah dalam komputasi, mesin ini akan dapat mengubah isi dari sel yang aktif, mengubah status dari komponen baca/tulis, dan mengubah posisi pita ke kiri atau ke kanan.

Sejarah

Jauh sebelum lahirnya program komputer, Alan Turing pada tahun 1936 telah mengeluarkan gagasannya berupa model mesin abstrak sebagai alat mekanik untuk mengerjakan prosedur yang efektif. Model ini disebut Mesin Turing.

Mesin turing dapat diadaptasi untuk mensimulasi logika dari setiap algoritma oleh karena itu cara kerja mesin turing adalah ekivalen dengan cara kerja komputer sekarang ini dan mesin turing juga ekivalen dengan problema komputasi matematika. Mesin turing tidak ditujukan sebagai teknologi komputasi praktis tetapi lebih sebagai eksperimen pemikiran yang mewakili sebuah mesin komputasi. Mesin turing membantu para ilmuan komputer memahami batas-batas komputasi mekanis.

Sebagai input dari mesin turing adalah kata atau untai atas suatu alfabet T. Mesin turing berhenti dengan keadaan menerima atau menolak untai. Kadang-kadang terjadi pula perulangan atau looping tak terhingga.

Keterangan:

· - Tape: Tempat diletakannya inputan yang berupa kata/untai.

· - Head: membaca dan menulisi sel pita mesin turing, bisa bergerak ke kiri atau ke kanan.

· - Finite StateControl (FSC): otak dari TM, diimplementasikan dari algoritma pengenalan kalimat.

Definisi Mesin Turing

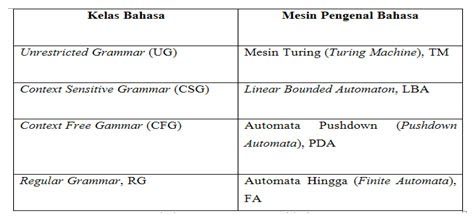
Mesin turing didefinisikan sebagai 7 tuple M={ Q, S, G, S, F, Ь, ∆}

Q: himpunan hingga state,

S: alfabet input,

G: simbol pada pita (meliputi pula blank)

S: state awal, S Î Q

Ь: simbol kosong (blank) (bukan bagian dari S )

∆: fungsi transisi

F: state akhir, F Î Q

Gerakan Mesin Turing

Gerakan mesin turing diwakili oleh fungsi transisi:

∆(qi,a)=(qj,b,X): Mesin kedudukan qi membaca simbol masukan a,

gerakan: mesin berubah ke status qj, menulis b dan posisi baca /tulis bergerak X (berupa R=gerak kekanan atau L=gerak kekiri).

II. Dimiliki mesin turing dengan definisi M ={ Q, S, G, S, F, Ь, ∆}

Q={q1,q2}

S = {a,b}

G = {a,b, Ь }

S={ q1}

F={ q2}

∆: ∆ (q1,a)= (q1,a,R)

 ∆ (q1,b)= (q1,a,R)

 ∆ (q1, Ь)= (q2, Ь,L)

Jika di inputkan string “abbba”, maka gerakan mesin turing akan menjadi seperti apa ?

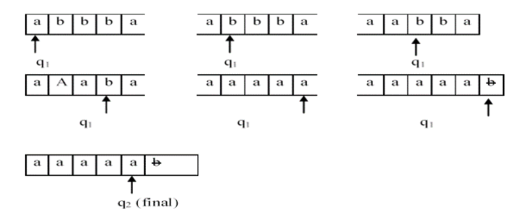
Contoh Mesin Turing Sederhana

Sebuah contoh mesin Turing dapat dibangun untuk melakukan komputasi sederhana yang didefinsikan seperti ini:

Tentukan ada berapa angka 1 dalam sebuah string berbentuk 0111...110 (rangkaian angka 1 yang didahului dengan 0 dan diakhiri juga dengan 0), apakah berjumlah genap atau berjumlah ganjil.

Jika angka 1 di antara dua angka 0 berjumlah genap, tulis sebuah angka 0 pada salah satu sel dari tape mesin Turing.

Jika angka 1 di antara dua angka 0 berjumlah ganjil, tulis sebuah angka 1 pada salah satu sel dari tape mesin Turing.

Untuk menyelesaikan masalah komputasi ini, kita buat tiga buah State bagi mesin Turing ini, yaitu Start, Even, dan Odd. Di samping itu kita buat sekumpulan aturan Transisi yang digunakan oleh

mesin Turing ini untuk melakukan proses komputasinya. Aturan-aturan Transisi tersebut dapat dituliskan demikian:

-Jika mesin Turing berada pada status Start, dan membaca simbol 0 pada Tape, lakukan hal berikut: Pindah status menjadi status Even, Ganti simbol 0 pada Tape dengan Blank (atau Hapus simbol 0 pada Tape), dan Bergerak ke kanan satu sel.

-Jika mesin Turing berada pada status Even, dan membaca simbol 1 pada Tape, lakukan hal berikut: Pindah status menjadi status Odd, Ganti simbol 1 pada Tape dengan Blank, dan Bergerak ke kanan satu sel.

Table^{[pranala nonaktif permanen]} Graphic Palindrome Detector

-Jika mesin Turing berada pada status Odd, dan membaca simbol 1 pada Tape, lakukan hal berikut: Pindah status menjadi Even, Ganti simbol 1 pada Tape dengan Blank, dan Bergerak ke kanan satu sel.

-Jika mesin Turing berada pada status Even, dan membaca simbol 0 pada Tape, lakukan hal berikut: Pindah status menjadi Halt, Ganti simbol 0 pada Tape dengan 0, dan tetap pada sel tersebut (tidak perlu berpindah ke kiri maupun ke kanan).

-Jika mesin Turing berada pada status Odd, dan membaca simbol 0 pada Tape, lakukan hal berikut: Pindah status menjadi Halt, Ganti simbol 0 pada Tape dengan 1, dan tetap pada sel tersebut.

Palindrome itu adalah berasal dari bahasa Yunani yaitu Palindromos A Palindrome. Palindromos A Palindrome adalah kata atau kalimat yang sama dieja maju atau mundur(bacaan yang sama dieja pada kedua arah). Sebagai contoh sederhana adalah beberapa kata yang sederhana yaitu rotor, rotator, civic, madam, racecar, level, dan lain-lain. Untuk contoh lain yaitu kalimat palindrome adalah No lemon no melon, No devil lived on, Swap God for a janitor rot in a jar of dog paws, dll.

Dibawah ini adalah graf dari palindrome detector, merupakan sebuah simulasi mesin turing yang berfungsi untuk mendeteksi kata palindrome yang diinputkan oleh user. Kata atau untai yang dibentuk masih terbatas pada penggunaan huruf “A” dan “B”. Contoh kata yang dibentuk adalah “ABAABBA” untuk kata yang tidak termasuk dalam palindrome, dan “BABBAB” untuk kata yang termasuk dalam palindrome.

Pemrograman sederhana jenis mesin Turing ini tidak sesulit yang dibayangkan. Dimana sebenarnya pemrograman ini akan membentuk graph. Transisi state terdiri dari 5-tupel rangkaian pada setiap baris, dengan format seperti ini:

[state],[karakter],[state baru],[karakterbaru],[arah]

1, _, 2, #, >

2, A, 3, A, >

Karakter '_' dapat digunakan untuk menunjukkan kosong(blank), 'H' untuk menunjukkan sebagai state berhenti/Halt (hanya berlaku pada sisi kanan transisi), dan '<' dan '>' untuk menunjukkan arah masing-masing bergerak kekiri atau kanan.

Lihat pula

Langton's ant, a simple two-dimensional analogue of the Turing machine.
Probabilistic Turing machine
Church-Turing thesis, which says Turing machines can perform any computation that can be performed.
Busy Beaver
Computability logic
Turing completeness
Turing tarpit, any computing system or language which, like the Turing machine, is not only Turing-complete but also useless for practical computing.
Neal Stephenson's Cryptonomicon

Referensi

Rolf Herken: The Universal Turing Machine - A Half-Century Survey, Springer Verlag, ISBN 3-211-82637-8
Paul Strathern: Turing and the Computer - The big idea, Anchor Books/Doubleday, ISBN 0-385-49243-X
Turing, A., On Computable Numbers, With an Application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, Series 2, Volume 42, 1936; reprinted in M. David (ed.), The Undecidable, Hewlett, NY: Raven Press, 1965;
Boolos, G. and Jeffrey, R., Computability and Logic, 2nd ed., Cambridge: Cambridge University Press, 1980.
Rogozhin, Yurii, "A Universal Turing Machine with 22 States and 2 Symbols" Diarsipkan 2005-03-08 di Wayback Machine., Romanian Journal Of Information Science and Technology, 1(3), 259-265, 1998. (surveys known results about small universal Turing machines)
Wolfram, Stephen, A New Kind of Science, Wolfram Media, ISBN 1-57955-008-8

Pranala luar

Turing Machine on Stanford Encyclopedia of Philosophy
Detailed info on the Church-Turing Hypothesis (Stanford Encyclopedia of Philosophy)
http://rizkyfajar09.blogspot.com/2014/02/tugas-teori-bahasa-dan-otomata-contoh.html
http://www.budiluhur.ac.id

Simulator

Visual Turing Machine, a visual designer and simulator, (free software, platform independent).
Visual Turing, a Turing machine interactive simulator/IDE Diarsipkan 2004-04-07 di Wayback Machine. (free software for Windows).
Suzanne Britton's Turing Machine Simulator (java applet).
C++ Simulator of a Nondeterministic and Deterministic Multitape Turing Machine Diarsipkan 2008-05-15 di Wayback Machine. (free software).
C++ Simulator of a Universal Turing Machine (which accepts Multitape Turing Machine) Diarsipkan 2005-09-13 di Wayback Machine. (free software).
Turing Train Terminal - A working Turing machine built out of scale trains.
TMML - Describing a Turing Machine with XML

Templat:Formal languages and grammars