Metode bagi-dua
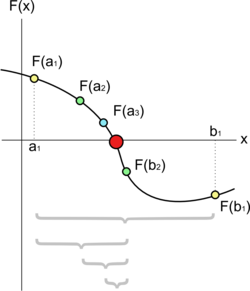
Dalam matematika, metode bagi-dua adalah algoritme pencarian akar yang membagi dua selang, lalu memilih bagian selang yang berisi akar seharusnya berada untuk diproses lebih lanjut. Metode ini sangat sederhana dan tangguh, tetapi juga sangat lambat. Metode ini juga memiliki sebutan metode setengah interval (interval halving method),[1] metode pencarian biner (binary search method),[2] atau metode dikotomi (dichotomy method).[3]
Metode
[sunting | sunting sumber]Metode ini berlaku ketika kita ingin memecahkan persamaan f(x) = 0 untuk variabel skalar x, di mana f merupakan fungsi kontinu.
Metode bagi-dua mensyaratkan dua titik awal a dan b sedemikian sehingga f(a) dan f(b) memiliki tanda berlainan. Ini dinamakan kurung dari sebuah akar. Menurut teorema nilai antara, fungsi f mestilah memiliki paling tidak satu akar dalam selang (a, b). Metode ini kemudian membagi selang menjadi dua dengan menghitung titik tengah c = (a + b) / 2 dari selang tersebut. Kecuali c sendiri merupakan akar persamaan, yang mungkin saja terjadi, tetapi cukup jarang, sekarang ada dua kemungkinan: f(a) dan f(c) memiliki tanda berlawanan dan mengapit akar, atau f(c) dan f(b) memiliki tanda berlawanan dan mengapit akar. Kita memilih bagian selang yang mengapit, dan menerapkan langkah bagi-dua serupa terhadapnya. Dengan cara ini selang yang mungkin mengandung nilai nol dari f dikurangi lebarnya sebesar 50% pada setiap langkah. Kita meneruskan langkah ini sampai kita memiliki selang yang dianggap cukup kecil.
Secara eksplisit: jika f(a) f(c) < 0, maka metode ini menetapkan b baru sama dengan c, dan bila f(b) f(c) < 0, maka metode ini menetapkan a baru sama dengan c. Dalam kedua kasus, f(a) dan f(b) baru memiliki tanda berlawanan, sehingga metode ini dapat diterapkan pada selang baru yang lebih kecil ini. Implementasi metode ini harus berjaga-jaga terhadap kemungkinan bahwa titik tengah ternyata merupakan pemecahan.[4]
Rujukan
[sunting | sunting sumber]- ^ "Interval Halving (Bisection)". Diarsipkan dari versi asli tanggal 2013-05-19. Diakses tanggal 2013-11-07.
- ^ Burden & Faires 1985, hlm. 28
- ^ "Dichotomy method - Encyclopedia of Mathematics". www.encyclopediaofmath.org. Diakses tanggal 2015-12-21.
- ^ Burden & Faires 1985, hlm. 28 for section
- Burden, Richard L.; Faires, J. Douglas (1985), "2.1 The Bisection Algorithm", Numerical Analysis
(edisi ke-3rd), PWS Publishers, ISBN 0-87150-857-5
 | Artikel bertopik matematika ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya. |