Tegak lurus: Perbedaan antara revisi
Dedhert.Jr (bicara | kontrib) Tidak ada ringkasan suntingan |
Tidak ada ringkasan suntingan Tag: Suntingan perangkat seluler Suntingan peramban seluler |
||
| (13 revisi perantara oleh 6 pengguna tidak ditampilkan) | |||
| Baris 1: | Baris 1: | ||
| ⚫ | |||
[[Berkas:Perpendicular-coloured.svg|ka|jmpl|250px|Garis AB berserenjang terhadap garis CD karena dua sudut yang diciptakannya (ditunjukkan dengan warna biru dan jingga) masing-masing berukuran 90 derajat.]] |
|||
Dalam [[geometri]] elementer, dua objek geometri dikatakan '''tegak lurus''' atau '''serenjang''' ({{lang-en|perpendicular}}) jika kedua objek tersebut saling [[Perpotongan (geometri)|berpotongan]] dan membentuk sudut siku-siku atau sudut tegak, dalam artian membentuk sudut 90 derajat atau π/2 radian.<ref name=":0">{{harvtxt|Kay|1969|p=91}}</ref> Dengan kata lain, tegak lurus dapat didefinisikan sebagai perpotongan dari dua garis, atau dua bidang, atau perpotongan antara sebuah garis dengan sebuah bidang. |
|||
| ⚫ | |||
Dalam [[geometri]] elementer, '''serenjang''', '''tegak lurus''' atau '''perpendikular''' ({{lang-en|perpendicular}}), adalah hubungan antara dua garis lurus yang bertemu di sebuah [[sudut tegak]]. |
|||
== Definisi == |
|||
Sebuah [[garis (geometri)|garis]] dikatakan berserenjang terhadap garis lainnya jika kedua garis tersebut berpotongan di sebuah sudut tegak.<ref>{{harvtxt|Kay|1969|p=91}}</ref> Secara eksplisit, garis pertama berserenjang terhadap garis kedua jika kedua garis bertemu, dan pada titik perpotongan [[sudut lurus]] di salah satu sisi, garis pertama dipotong oleh garis kedua menjadi dua [[sudut]] [[kongruen]]. Serenjang harus digambar secara [[simetris]], artinya jika garis pertama berserenjang terhadap garis kedua, maka garis kedua juga berserenjang terhadap garis pertama. Oleh sebab itu, dua garis bisa berserenjang satu sama lainnya tanpa harus digambar secara berurutan. |
|||
Sebuah [[garis (geometri)|garis]] dikatakan tegak lurus terhadap garis lainnya jika kedua garis tersebut berpotongan di sebuah sudut tegak. Secara eksplisit, garis pertama tegak lurus terhadap garis kedua jika kedua garis bertemu, dan pada titik perpotongan [[Sudut (geometri)|sudut lurus]] di salah satu sisi, garis pertama dipotong oleh garis kedua menjadi dua [[sudut]] [[kongruen]]. Sifat tegak lurus adalah [[simetris]], artinya jika garis pertama tegak lurus terhadap garis kedua, maka garis kedua juga tegak lurus terhadap garis pertama. Oleh sebab itu, dua garis bisa tegak lurus satu sama lainnya tanpa harus digambar secara berurutan.[[Berkas:Perpendicular-coloured.svg|jmpl|250px|Garis <math>\overline{AB}</math> tegak lurus terhadap garis <math>\overline{CD}</math> karena dua sudut yang diciptakannya (ditunjukkan dengan warna biru dan jingga) masing-masing berukuran 90 derajat.|kiri]]Berdasarkan gambar di samping, garis <math>\overline{AB}</math> tegak lurus terhadap garis <math>\overline{CD}</math> jika masing-masing garis diperpanjang di kedua arah untuk membentuk garis tak hingga, sehingga menghasilkan dua garis yang saling tegak lurus. Hal tersebut dapat ditulis dalam bentuk simbol, yaitu <math>\overline{AB} \perp \overline{CD}</math>, yang berarti garis <math>\overline{AB}</math> tegak lurus terhadap garis <math>\overline{CD}</math>.<ref name=":0" /> Titik <math>B</math> disebut dengan '''kaki tegak lurus dari '''<math>A</math> '''ke garis <math>\overline{CD}</math>''', atau '''kaki ''<math>A</math>'' pada <math>\overline{CD}</math>'''.<ref>{{harvtxt|Kay|1969|p=114}}</ref> |
|||
| ⚫ | |||
Berdasarkan gambar di samping, garis <math>\overline{AB}</math> berserenjang terhadap garis <math>\overline{CD}</math> jika masing-masing garis diperpanjang di kedua arah untuk membentuk garis tak hingga, sehingga menghasilkan dua garis yang saling berserenjang. Dalam simbol, persamaannya adalah <math>\overline{AB} \perp \overline{CD}</math>, dibaca: garis AB berserenjang terhadap garis CD.<ref>{{harvtxt|Kay|1969|p=91}}</ref> Titik ''B'' disebut dengan '''kaki serenjang dari ''A'' ke garis <math>\overline{CD}</math>''', atau '''kaki ''A'' pada <math>\overline{CD}</math>'''.<ref>{{harvtxt|Kay|1969|p=114}}</ref> |
|||
{{Clear}} |
|||
| ⚫ | |||
== Lihat juga == |
== Lihat juga == |
||
| Baris 26: | Baris 26: | ||
* [http://www.mathopenref.com/constbisectline.html How to draw a perpendicular bisector of a line with compass and straight edge] Animated demonstration |
* [http://www.mathopenref.com/constbisectline.html How to draw a perpendicular bisector of a line with compass and straight edge] Animated demonstration |
||
* [http://www.mathopenref.com/constperpendray.html How to draw a perpendicular at the endpoint of a ray with compass and straight edge] Animated demonstration |
* [http://www.mathopenref.com/constperpendray.html How to draw a perpendicular at the endpoint of a ray with compass and straight edge] Animated demonstration |
||
| ⚫ | |||
[[Kategori:Geometri dasar]] |
[[Kategori:Geometri dasar]] |
||
[[Kategori:Orientasi]] |
[[Kategori:Orientasi]] |
||
| ⚫ | |||
Revisi terkini sejak 10 Januari 2024 05.13
| Geometri |
|---|
 |
| Ahli geometri |
Dalam geometri elementer, dua objek geometri dikatakan tegak lurus atau serenjang (bahasa Inggris: perpendicular) jika kedua objek tersebut saling berpotongan dan membentuk sudut siku-siku atau sudut tegak, dalam artian membentuk sudut 90 derajat atau π/2 radian.[1] Dengan kata lain, tegak lurus dapat didefinisikan sebagai perpotongan dari dua garis, atau dua bidang, atau perpotongan antara sebuah garis dengan sebuah bidang.
Definisi
[sunting | sunting sumber]Sebuah garis dikatakan tegak lurus terhadap garis lainnya jika kedua garis tersebut berpotongan di sebuah sudut tegak. Secara eksplisit, garis pertama tegak lurus terhadap garis kedua jika kedua garis bertemu, dan pada titik perpotongan sudut lurus di salah satu sisi, garis pertama dipotong oleh garis kedua menjadi dua sudut kongruen. Sifat tegak lurus adalah simetris, artinya jika garis pertama tegak lurus terhadap garis kedua, maka garis kedua juga tegak lurus terhadap garis pertama. Oleh sebab itu, dua garis bisa tegak lurus satu sama lainnya tanpa harus digambar secara berurutan.
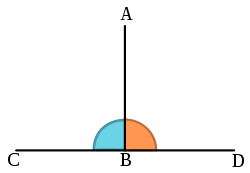
Berdasarkan gambar di samping, garis tegak lurus terhadap garis jika masing-masing garis diperpanjang di kedua arah untuk membentuk garis tak hingga, sehingga menghasilkan dua garis yang saling tegak lurus. Hal tersebut dapat ditulis dalam bentuk simbol, yaitu , yang berarti garis tegak lurus terhadap garis .[1] Titik disebut dengan kaki tegak lurus dari ke garis , atau kaki pada .[2]
Dalam ruang, dua bidang dikatakan tegak lurus jika sudut dihedral tempat kedua bidang bertemu berbentuk sudut tegak (90 derajat). Dalam matematika, sifat tegak lurus disebut dengan ortogonalitas, dan umum digunakan, misalnya dalam sistem koordinat Kartesius.
Lihat juga
[sunting | sunting sumber]- Ortogonalitas (pada matematika)
- Paralel (geometri)
- Komponen serenjang (pada vektor)
Catatan
[sunting | sunting sumber]Referensi
[sunting | sunting sumber]- Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (edisi ke-2nd), New York: Barnes & Noble, LCCN 52-13504
- Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69-12075
Pranala luar
[sunting | sunting sumber]- Definition: perpendicular With interactive animation
- How to draw a perpendicular bisector of a line with compass and straight edge Animated demonstration
- How to draw a perpendicular at the endpoint of a ray with compass and straight edge Animated demonstration





