Garis (geometri): Perbedaan antara revisi
k Bot: Perubahan kosmetika |
perbaikan kecil |
||
| Baris 1: | Baris 1: | ||
[[Berkas:1D line.svg|310px|jmpl|Contoh satu [[ruas garis]]]] |
[[Berkas:1D line.svg|310px|jmpl|Contoh satu [[ruas garis]]]] |
||
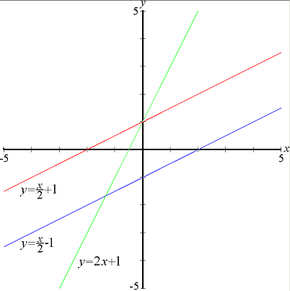
[[Berkas:Linear functions2.PNG|290px|jmpl|Tiga garis — garis merah dan biru memiliki kemiringan yang sama, sementara garis merah dan hijau memiliki persilangan y yang sama.]] |
[[Berkas:Linear functions2.PNG|290px|jmpl|Tiga garis — garis merah dan biru memiliki kemiringan yang sama, sementara garis merah dan hijau memiliki persilangan y yang sama.]] |
||
'''Garis''' ( |
'''Garis''' ({{lang-en|line}}), dalam [[geometri Euklides]], adalah sebuah [[lengkungan]] [[kelengkungan|lurus]]. Ketika geometri digunakan untuk me[[model (ilmu pengetahuan)|model]] dunia nyata, garis digunakan untuk menggambarkan objek lurus dengan lebar dan tinggi yang berbeda. Garis adalah idealisasi dari objek semacam itu dan tidak punya lebar atau tinggi dan panjangnya dianggap [[tak hingga]]. |
||
Dalam [[geometri]], sebuah garis biasanya merupakan satu [[anggapan primitif]] dari [[sistem aksioma]]. Garis terdiri dari [[himpunan (matematika)|himpunan]] [[titik (geometri)|titik]] dan merupakan [[subhimpunan]] dari [[bidang (geometri)|bidang]]. Dalam [[geometri diferensial]], konsep garis digeneralisasikan menjadi [[geodesi]]. Dalam [[geometri sintetis]], sebuah garis adalah satu anggapan lama dalam sistem [[Euklides]], [[Karl von Staudt]], dan [[David Hilbert]]. Sebuah garis adalah sebutan terdefinisikan dalam sistem [[Giuseppe Peano]], [[Mario Pieri]] dan [[Alessandro Padoa]]. |
Dalam [[geometri]], sebuah garis biasanya merupakan satu [[anggapan primitif]] dari [[sistem aksioma]]. Garis terdiri dari [[himpunan (matematika)|himpunan]] [[titik (geometri)|titik]] dan merupakan [[subhimpunan]] dari [[bidang (geometri)|bidang]]. Dalam [[geometri diferensial]], konsep garis digeneralisasikan menjadi [[geodesi]]. Dalam [[geometri sintetis]], sebuah garis adalah satu anggapan lama dalam sistem [[Euklides]], [[Karl von Staudt]], dan [[David Hilbert]]. Sebuah garis adalah sebutan terdefinisikan dalam sistem [[Giuseppe Peano]], [[Mario Pieri]] dan [[Alessandro Padoa]]. |
||
Sebuah |
Sebuah [[ruas garis]] adalah bagian dari garis yang dikelilingi oleh dua ujung berbeda dan terdiri dari setiap titik di garis antara kedua ujungnya. Tergantung cara ruas garis ini dideginisikan, satu dari dua ujung tersebut bisa jadi atau bukan bagian dari ruas garis. Dua ruas garis atau lebih bisa memiliki hubungan yang sama seperti garis, seperti paralel, perpotongan, atau kemiringan. |
||
== Lihat pula == |
== Lihat pula == |
||
| Baris 20: | Baris 21: | ||
== Pranala luar == |
== Pranala luar == |
||
* {{MathWorld |urlname=Line |title=Line}} |
* {{MathWorld |urlname=Line |title=Line}} |
||
* [http://www.cut-the-knot.org/Curriculum/Calculus/StraightLine.shtml Equations of the Straight Line] at [[Cut-the-Knot]] |
* {{en}} [http://www.cut-the-knot.org/Curriculum/Calculus/StraightLine.shtml Equations of the Straight Line] at [[Cut-the-Knot]] |
||
* [http://en.citizendium.org/wiki/Line_(geometry) Citizendium] |
* {{en}} [http://en.citizendium.org/wiki/Line_(geometry) Citizendium] |
||
{{bangun}} |
{{bangun}} |
||
Revisi per 20 Juni 2018 15.35

Garis (bahasa Inggris: line), dalam geometri Euklides, adalah sebuah lengkungan lurus. Ketika geometri digunakan untuk memodel dunia nyata, garis digunakan untuk menggambarkan objek lurus dengan lebar dan tinggi yang berbeda. Garis adalah idealisasi dari objek semacam itu dan tidak punya lebar atau tinggi dan panjangnya dianggap tak hingga.
Dalam geometri, sebuah garis biasanya merupakan satu anggapan primitif dari sistem aksioma. Garis terdiri dari himpunan titik dan merupakan subhimpunan dari bidang. Dalam geometri diferensial, konsep garis digeneralisasikan menjadi geodesi. Dalam geometri sintetis, sebuah garis adalah satu anggapan lama dalam sistem Euklides, Karl von Staudt, dan David Hilbert. Sebuah garis adalah sebutan terdefinisikan dalam sistem Giuseppe Peano, Mario Pieri dan Alessandro Padoa.
Sebuah ruas garis adalah bagian dari garis yang dikelilingi oleh dua ujung berbeda dan terdiri dari setiap titik di garis antara kedua ujungnya. Tergantung cara ruas garis ini dideginisikan, satu dari dua ujung tersebut bisa jadi atau bukan bagian dari ruas garis. Dua ruas garis atau lebih bisa memiliki hubungan yang sama seperti garis, seperti paralel, perpotongan, atau kemiringan.
Lihat pula
Catatan kaki
Bahan pustaka
- Faber, Richard L. (1983). Foundations of Euclidean and Non-Euclidean Geometry. New York, United States: Marcel Dekker. ISBN 0-8247-1748-1.
Pranala luar
- (Inggris) Weisstein, Eric W. "Line". MathWorld.
- (Inggris) Equations of the Straight Line at Cut-the-Knot
- (Inggris) Citizendium
