Lingkaran: Perbedaan antara revisi
Tag: Pembatalan |
Menambahkan subjudul sejarah dan gambar |
||
| Baris 16: | Baris 16: | ||
== Definisi topologis == |
== Definisi topologis == |
||
Di bidang topologi, lingkaran tidak terbatas pada konsep geometris, tetapi untuk semua [[homeomorfisme]]<nowiki/>nya. Dua lingkaran topologi setara jika satu dapat ditransformasikan menjadi yang lain melalui deformasi '''R'''<sup>3</sup> pada dirinya sendiri (dikenal sebagai [[ambient isotopy]])<ref>{{Cite journal|last=|first=|year=|title=Gamelin, Theodore (1999). Pengantar topologi. Mineola, N.Y: Publikasi Dover.|url=https://en.wiki-indonesia.club/wiki/Special:BookSources/0486406806|journal=Wikipedia|language=en|volume=|issue=|pages=|doi=}}</ref> |
Di bidang topologi, lingkaran tidak terbatas pada konsep geometris, tetapi untuk semua [[homeomorfisme]]<nowiki/>nya. Dua lingkaran topologi setara jika satu dapat ditransformasikan menjadi yang lain melalui deformasi '''R'''<sup>3</sup> pada dirinya sendiri (dikenal sebagai [[ambient isotopy]])<ref>{{Cite journal|last=|first=|year=|title=Gamelin, Theodore (1999). Pengantar topologi. Mineola, N.Y: Publikasi Dover.|url=https://en.wiki-indonesia.club/wiki/Special:BookSources/0486406806|journal=Wikipedia|language=en|volume=|issue=|pages=|doi=}}</ref> |
||
== Sejarah == |
|||
Dalam bahasa [[Inggris]], lingkaran disebut dengan ''circle'' serta memiliki kaitan yang erat dengan kata ''circus'' ataupun ''circuit.'' Sementara itu, lingkaran dalam bahasa [[Yunani]] adalah κίρκος/κύκλος (''kirkos/kuklos'') yang merupakan metatesis dari bahasa Yunani homerik yaitu κρίκος atau ''krikos'' artinya cincin, gelang, atau simpai.<ref>{{Cite web|title=Henry George Liddell, Robert Scott, A Greek-English Lexicon, κρίκ-ος|url=http://www.perseus.tufts.edu/hopper/text?doc=Perseus:text:1999.04.0057:entry=kri/kos|website=www.perseus.tufts.edu|access-date=2020-08-29}}</ref> |
|||
[[Berkas:Shatir500.jpg|al=Gambar lingkaran dalam arstronomi Arab kuno|jmpl|Gambar lingkaran dalam arstronomi Arab kuno]] |
|||
adalah ''κίρκος/κύκλος (kirkos/kukl''. ''os)'' |
|||
== Istilah dalam lingkaran == |
== Istilah dalam lingkaran == |
||
| Baris 139: | Baris 147: | ||
Panjang busur adalah <math>\frac{\theta}{360} 2 \pi r </math> atau <math>\theta r</math> |
Panjang busur adalah <math>\frac{\theta}{360} 2 \pi r </math> atau <math>\theta r</math> |
||
== Garis singgung lingkaran == |
|||
== π (Pi) == |
== π (Pi) == |
||
Revisi per 29 Agustus 2020 06.32
| Lingkaran | |
|---|---|
 Sebuah lingkaran (hitam), yang diukur dengan kelilingnya ( C ), diameter ( D ) dalam cyan, dan jari-jari ( R ) dalam warna merah; pusatnya ( O ) ada di magenta.
|
| Geometri |
|---|
 |
| Ahli geometri |
Lingkaran adalah bentuk yang terdiri dari semua titik dalam bidang yang berjarak tertentu dari titik tertentu, pusat; ekuivalennya adalah kurva yang dilacak oleh titik yang bergerak dalam bidang sehingga jaraknya dari titik tertentu adalah konstan. Jarak antara titik mana pun dari lingkaran dan pusat disebut jari-jari. Artikel ini adalah tentang lingkaran dalam geometri Euclidean, dan, khususnya, bidang Euclidean, kecuali jika dinyatakan sebaliknya.
Secara khusus, sebuah lingkaran adalah kurva tertutup sederhana yang membagi pesawat menjadi dua wilayah: interior dan eksterior. Dalam penggunaan sehari-hari, istilah "lingkaran" dapat digunakan secara bergantian untuk merujuk pada batas gambar, atau keseluruhan gambar termasuk bagian dalamnya; dalam penggunaan teknis yang ketat, lingkaran hanyalah batas dan seluruh gambar disebut cakram.
Lingkaran juga dapat didefinisikan sebagai jenis elips khusus di mana dua fokus bertepatan dan eksentrisitasnya adalah 0, atau bentuk dua dimensi yang melingkupi area per satuan perimeter kuadrat, menggunakan kalkulus variasi.
Definisi Euclid
Lingkaran adalah sosok bidang yang dibatasi oleh satu garis lengkung, dan sedemikian rupa sehingga semua garis lurus yang ditarik dari titik tertentu di dalamnya ke garis pembatas, adalah sama. Garis pembatas disebut kelilingnya dan titiknya, pusatnya.
Definisi topologis
Di bidang topologi, lingkaran tidak terbatas pada konsep geometris, tetapi untuk semua homeomorfismenya. Dua lingkaran topologi setara jika satu dapat ditransformasikan menjadi yang lain melalui deformasi R3 pada dirinya sendiri (dikenal sebagai ambient isotopy)[2]
Sejarah
Dalam bahasa Inggris, lingkaran disebut dengan circle serta memiliki kaitan yang erat dengan kata circus ataupun circuit. Sementara itu, lingkaran dalam bahasa Yunani adalah κίρκος/κύκλος (kirkos/kuklos) yang merupakan metatesis dari bahasa Yunani homerik yaitu κρίκος atau krikos artinya cincin, gelang, atau simpai.[3]

adalah κίρκος/κύκλος (kirkos/kukl. os)
Istilah dalam lingkaran
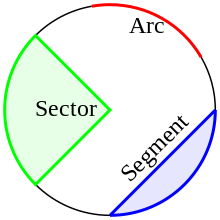
Beberapa istilah geometri mengenai lingkaran, yaitu:
- Titik pusat (P): merupakan titik tengah lingkaran, di mana jarak titik tersebut dengan titik manapun pada lingkaran selalu tetap.
- Jari-jari (R): merupakan garis lurus yang menghubungkan titik pusat dengan lingkaran.
- Tali busur (TB): merupakan garis lurus di dalam lingkaran yang memotong lingkaran pada dua titik yang berbeda.
- Busur (B): merupakan garis lengkung baik terbuka, maupun tertutup yang berimpit dengan lingkaran.
- Keliling lingkaran (K): merupakan busur terpanjang pada lingkaran.
- Diameter (D):merupakan tali busur terbesar yang panjangnya adalah dua kali dari jari-jarinya. Diameter ini membagi lingkaran sama luas.
- Apotema : merupakan garis terpendek antara tali busur dan pusat lingkaran.
- Juring (J): merupakan daerah pada lingkaran yang dibatasi oleh busur dan dua buah jari-jari yang berada pada kedua ujungnya.
- Tembereng (T): merupakan daerah pada lingkaran yang dibatasi oleh sebuah busur dengan tali busurnya.
- Cakram (C): merupakan semua daerah yang berada di dalam lingkaran. Luasnya yaitu jari-jari kuadrat dikalikan dengan pi. Cakram merupakan juring terbesar.
 |
 |
Persamaan
Suatu lingkaran memiliki persamaan
dengan adalah jari-jari lingkaran dan adalah koordinat pusat lingkaran.
Jika pusat lingkaran terdapat di , maka persamaan di atas dapat dituliskan sebagai
Bentuk persamaan lingkaran dapat dijabarkan juga menjadi bentuk
dengan adalah jari-jari lingkaran dan adalah koordinat pusat lingkaran. Bentuk persamaan tersebut dikenal sebagai bentuk umum persamaan lingkaran.
Persamaan parametrik
Lingkaran dapat pula dirumuskan dalam suatu persamaan parameterik, yaitu
yang apabila dibiarkan menjalani t akan dibuat suatu lintasan berbentuk lingkaran dalam ruang x-y.
Luas lingkaran

Luas lingkaran memiliki rumus
yang dapat diturunkan dengan melakukan integrasi elemen luas suatu lingkaran
dalam koordinat polar, yaitu
Dengan cara yang sama dapat pula dihitung luas setengah lingkaran, seperempat lingkaran, dan bagian-bagian lingkaran. Juga tidak ketinggalan dapat dihitung luas suatu cincin lingkaran dengan jari-jari dalam dan jari-jari luar .
Penjumlahan elemen juring
Luas lingkaran dapat dihitung dengan memotong-motongnya sebagai elemen-elemen dari suatu juring untuk kemudian disusun ulang menjadi sebuah persegi panjang yang luasnya dapat dengan mudah dihitung. Dalam gambar r berarti sama dengan R yaitu jari-jari lingkaran.
Luas juring
Luas juring suatu lingkaran dapat dihitung apabila luas lingkaran dijadikan fungsi dari R dan θ, yaitu;
dengan batasan nilai θ adalah antara 0 dan 2π. Saat θ bernilai 2π, juring yang dihitung adalah juring terluas, atau luas lingkaran.
Luas juring adalah atau
Luas tembereng
Luas tembereng = Luas juring - Luas segitiga sama kaki.
Luas cincin lingkaran
Suatu cincin lingkaran memiliki luas yang bergantung pada jari-jari dalam dan jari-jari luar , yaitu
di mana untuk rumus ini kembali menjadi rumus luas lingkaran.
Luas potongan cincin lingkaran
Dengan menggabungkan kedua rumus sebelumnya, dapat diperoleh
yang merupakan luas sebuah cincin tak utuh.
Keliling lingkaran
Keliling lingkaran memiliki rumus:
Panjang busur lingkaran
Panjang busur suatu lingkaran dapat dihitung dengan menggunakan rumus
yang diturunkan dari rumus untuk menghitung panjang suatu kurva
di mana digunakan
sebagai kurva yang membentuk lingkaran. Tanda mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.
Panjang busur adalah atau
Garis singgung lingkaran
π (Pi)
Templat:Mainarticle Nilai pi adalah suatu besaran yang merupakan sifat khusus dari lingkaran, yaitu perbandingan dari keliling K dengan diameternya D:[a]
Catatan kaki
Referensi
- ^ "Irrational Numbers". Diakses tanggal 2019-08-12.
- ^ "Gamelin, Theodore (1999). Pengantar topologi. Mineola, N.Y: Publikasi Dover". Wikipedia (dalam bahasa Inggris).
- ^ "Henry George Liddell, Robert Scott, A Greek-English Lexicon, κρίκ-ος". www.perseus.tufts.edu. Diakses tanggal 2020-08-29.
- ^ "Irrational Numbers". Diakses tanggal 2019-08-12.
- ^ "Proving Pi is Irrational: a step-by-step guide to a "simple proof" requiring only high school calculus – Mind Your Decisions".
- ^ "Pi - Proof that Pi is Irrational". crypto.stanford.edu.
Pustaka
- Pedoe, Dan (1988). Geometry: a comprehensive course. Dover.
- "Circle" in The MacTutor History of Mathematics archive
Pranala luar
- Hazewinkel, Michiel, ed. (2001) [1994], "Circle", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
- Circle di PlanetMath.org.
- (Inggris) Weisstein, Eric W. "Circle". MathWorld.
- Interactive Java applets untuk sifat dan konstruksi dasar yang melibatkan lingkaran.
- Interactive Standard Form Equation of Circle Klik dan seret poin untuk melihat persamaan bentuk standar dalam aksi
- Munching on Circles at cut-the-knot
































