Deret Fourier: Perbedaan antara revisi
k v2.04b - Fixed using Wikipedia:ProyekWiki Cek Wikipedia (Kesalahan pranala pipa) |
Tag: Suntingan perangkat seluler Suntingan peramban seluler Suntingan seluler lanjutan |
||
| Baris 357: | Baris 357: | ||
|Berkas:Fourier Series.svg| |
|Berkas:Fourier Series.svg| |
||
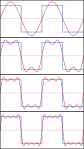
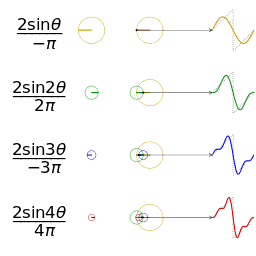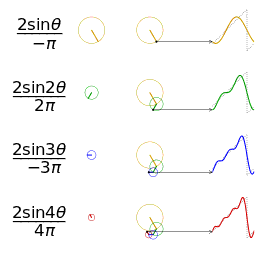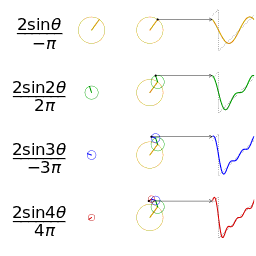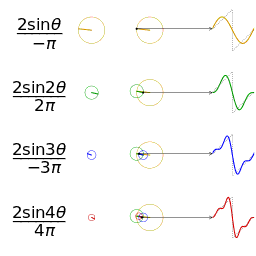
Empat jumlah parsial pertama dari deret Fourier untuk [[gelombang persegi]] |
Empat jumlah parsial pertama dari deret Fourier untuk [[gelombang persegi]] |
||
|Berkas:SquareWaveFourierArrows%2Crotated.gif |
|Berkas:SquareWaveFourierArrows%2Crotated-id.gif |
||
}} |
}} |
||
Revisi per 16 Maret 2022 22.33
| Transformasi Fourier |
|---|
Dalam matematika, Deret Fourier (/ˈfʊrieɪ, -iər/[1]) merupakan penguraian fungsi periodik menjadi jumlahan fungsi-fungsi berosilasi, yaitu fungsi sinus dan kosinus, ataupun eksponensial kompleks. Studi deret Fourier merupakan cabang analisis Fourier. Deret Fourier diperkenalkan oleh Joseph Fourier (1768-1830) untuk memecahkan masalah persamaan panas di lempeng logam.
Persamaan panas merupakan persamaan diferensial parsial. Sebelum Fourier, pemecahan persamaan panas ini tidak diketahui secara umum, meskipun solusi khusus diketahui bila sumber panas berperilaku dalam cara sederhana, terutama bila sumber panas merupakan gelombang sinus atau kosinus. Solusi sederhana ini saat ini kadang-kadang disebut sebagai solusi eigen. Gagasan Fourier adalah memodelkan sumber panas ini sebagai superposisi (atau kombinasi linear) gelombang sinus dan kosinus sederhana, dan menuliskan pemecahannya sebagai superposisi solusi eigen terkait. Superposisi kombinasi linear ini disebut sebagai deret Fourier.
Meskipun motivasi awal adalah untuk memecahkan persamaan panas, kemudian terlihat jelas bahwa teknik serupa dapat diterapkan untuk sejumlah besar permasalahan fisika dan matematika. Deret Fourier saat ini memiliki banyak penerapan di bidang teknik elektro, analisis vibrasi, akustika, optika, pengolahan citra, mekanika kuantum, dan lain-lain.
Definisi
Pertimbangkan fungsi bernilai nyata, , yaitu integrable pada interval panjang , yang akan menjadi periode deret Fourier. Contoh umum interval analisis adalah:
- dan
- dan
Analisis proses menentukan bobot, diindeks dengan integer , yang merupakan jumlah siklus nilai harmonik dalam interval analisis. Oleh karena itu, panjang suatu siklus, dalam satuan , ialah . Dan frekuensi harmonik yang sesuai adalah . harmonik nilai dan , dan amplitudo (bobot) mereka ditemukan dengan integrasi selama interval panjang :[2]
Koefisien Fourier (Eq.1)
- Jika nilai ialah nilai dari nilai periodik, maka setiap interval dengan panjang tersebut sudah cukup.
- Nilai dan dapat direduksi menjadi nilai dan .
- Banyaknya teks memilih nilai untuk menyederhanakan argumen dari fungsi sinusoid.
Definisi 2
Proses sintesis (Deret Fourier sebenarnya) adalah:
Deret Fourier, bentuk sinus-kosinus (Eq.2)
Secara umum, integer pada nilai secara teoritis tidak terbatas. Meski begitu, deretan tersebut mungkin tidak konvergen atau persis sama di semua nilai (seperti diskontinuitas satu titik) dalam interval analisis. Untuk fungsi "berperilaku baik" yang khas dari proses fisik, kesetaraan biasanya diasumsikan.

Jika adalah fungsi yang terdapat dalam interval panjang (dan nol di tempat lain), kuadran kanan atas adalah contoh dari koefisien deret Fourier Pada nilak () mungkin terlihat seperti ketika diplot terhadap frekuensi harmonik yang sesuai. Kuadran kiri atas adalah transformasi Fourier yang sesuai dari Penjumlahan deret Fourier (tidak diperlihatkan) mensintesis penjumlahan periodik sedangkan invers Fourier transform (tidak ditampilkan) hanya mensintesis Menggunakan identitas trigonometri:
dan definisi nilai dan , pasangan sinus dan kosinus dapat dinyatakan sebagai sinusoid tunggal dengan offset fase, analog dengan konversi antara koordinat ortogonal (Kartesius) dan polar:
Deret Fourier, bentuk fase amplitudo (Eq.3)
Bentuk kebiasaan untuk menggeneralisasi menjadi bernilai kompleks (bagian selanjutnya) diperoleh dengan menggunakan rumus Euler untuk membagi fungsi kosinus menjadi eksponensial kompleks. Di sini, konjugasi kompleks dilambangkan dengan tanda bintang:
Oleh karena itu, dengan definisi:
hasil akhirnya adalah:
Deret Fourier, bentuk eksponensial (Eq.4)
Konvergensi
Dalam aplikasi rekayasa, deret Fourier umumnya dianggap berkumpul hampir di semua tempat (pengecualian berada pada diskontinuitas diskrit) karena fungsi yang ditemui dalam teknik berperilaku lebih baik daripada fungsi yang dapat diberikan oleh ahli matematika sebagai contoh tandingan untuk pres ini. Secara khusus, jika kontinu dan turunan dari (yang mungkin tidak ada di semua tempat) adalah integratif persegi, kemudian deret Fourier menyatu secara mutlak dan seragam ke nilai .[3] Jika suatu fungsi adalah integral-persegi pada interval , kemudian deret Fourier menyatu dengan fungsi di hampir setiap titik. Konvergensi deret Fourier juga bergantung pada jumlah hingga maksimal dan minimal dalam suatu fungsi yang dikenal sebagai salah satu Kondisi dirichlet untuk deret Fourier. Lihat Konvergensi seri Fourier. Koefisien Fourier dapat didefinisikan untuk fungsi atau distribusi yang lebih umum, dalam kasus seperti itu konvergensi dalam norma atau konvergensi lemah biasanya berupa inte.
-
Empat jumlah parsial (deret Fourier) dengan panjang 1, 2, 3, dan 4, menunjukkan bagaimana pendekatan terhadap gelombang persegi meningkat seiring dengan bertambahnya jumlah suku (animasi)
-
Empat jumlah parsial (deret Fourier) dengan panjang 1, 2, 3, dan 4, menunjukkan bagaimana pendekatan terhadap gelombang gigi gergaji meningkat seiring dengan bertambahnya jumlah suku (animasi)
-
Contoh konvergensi ke fungsi yang agak sewenang-wenang. Perhatikan perkembangan "dering" (fenomena Gibbs) pada transisi ke / dari bagian vertikal.
Animasi interaktif dapat dilihat lihat.
Contoh
Contoh 1: Deret Fourier sederhana

Plot dari gelombang gigi gergaji, kelanjutan periodik dari fungsi linier on the interval 
Plot animasi dari lima seri Fourier parsial pertama yang berurutan Kami sekarang menggunakan rumus di atas untuk memberikan perluasan deret Fourier dari fungsi yang sangat sederhana. Pertimbangkan gelombang gigi gergaji
Dalam hal ini, koefisien Fourier diberikan oleh
Terbukti bahwa seri Fourier konvergen di setiap titik dari mana dapat dibedakan, dan karenanya:
-
(Eq.7)
Kapan nilai , deret Fourier bertemu dengan 0, yang merupakan penjumlahan separuh dari batas kiri dan kanan s pada nilai . Ini adalah contoh khusus dari Teorema Dirichlet untuk deret Fourier.

Distribusi panas dalam pelat logam, menggunakan metode Fourier Contoh ini mengarahkan kita ke solusi untuk Masalah Basel.
Contoh 2: Motivasi Fourier
Perluasan deret Fourier dari fungsi kita pada Contoh 1 terlihat lebih rumit daripada rumus sederhana pada nilai , jadi tidak segera jelas mengapa seseorang membutuhkan seri Fourier. Meskipun ada banyak penerapan, motivasi Fourier adalah dalam memecahkan persamaan panas. Misalnya, perhatikan pelat logam berbentuk persegi yang sisinya berukuran meter, dengan koordinat . Jika tidak ada sumber panas di dalam pelat, dan jika tiga dari empat sisi ditahan pada 0 derajat Celcius, sedangkan sisi keempat, diberikan oleh nilai , dipertahankan pada gradien suhu derajat Celsius, untuk pada nilai , maka seseorang dapat menunjukkan bahwa distribusi panas stasioner (atau distribusi panas setelah periode waktu yang lama telah berlalu) diberikan oleh
Di sini, sin adalah fungsi sinus hiperbolik. Solusi persamaan panas tersebut diperoleh dengan cara mengalikan Eq.7 menurut nilai .
Aplikasi lain
Aplikasi lain dari deret Fourier yaitu untuk menyelesaikan Masalah Basel dengan menggunakan Teorema Parseval. Contoh tersebut menggeneralisasi dan seseorang dapat menghitung ζ(2n), untuk bilangan bulat positif apa pun nilai n.
Properti
Tabel properti dasar
Tabel ini menunjukkan beberapa operasi matematika dalam domain waktu dan efek yang sesuai dalam koefisien deret Fourier. Notasi:
- adalah konjugasi kompleks dari fungsi .
- menunjuk -fungsi periodik yang ditentukan dari fungsi .
- tentukan koefisien deret Fourier (bentuk eksponensial) dari fungsi dan seperti yang didefinisikan dalam persamaan Eq.5.
Properti Domain waktu Domain frekuensi (bentuk eksponensial) Catatan Referensi Linearitas bilangan kompleks Pembalikan waktu / Pembalikan frekuensi [4] Konjugasi waktu [4] Pembalikan waktu & konjugasi Bagian nyata dalam waktu Bagian waktu imajiner Bagian nyata dalam frekuensi Bagian imajiner dalam frekuensi Pergeseran waktu / modulasi frekuensi real number [4] Pergeseran frekuensi / Modulasi dalam waktu integer [4] Properti simetri
Ketika bagian nyata dan imajiner dari fungsi kompleks didekomposisi menjadi bagian genap dan ganjil, ada empat komponen, di bawah ini dilambangkan dengan subskrip RE, RO, IE, dan IO. Dan ada pemetaan satu-ke-satu antara empat komponen fungsi waktu kompleks dan empat komponen transformasi frekuensi kompleksnya:[5]
Lemma Riemann–Lebesgue
Kalau adalah integrable dari nilai , and Hasil ini dikenal sebagai Riemann–Lebesgue lemma.
Properti turunan
Jika Milik , setelah itu .
Jika nilai adalah koefisien dan lalu ada fungsi unik seperti yang untuk setiap nilai .
Teorema konvolusi
Grup kompak
Fungsi bernilai kompleks
Jika nilai adalah fungsi bernilai kompleks dari variabel nyata kedua komponen (bagian nyata dan imajiner) adalah fungsi bernilai nyata yang dapat direpresentasikan oleh deret Fourier. Kedua kumpulan koefisien dan jumlah parsial diberikan oleh:
- and
Mendefinisikan nilai menghasilkan:
(Eq.5)
Hal tersebut identik dengan Eq.4 selain nilai dan bukan lagi konjugasi kompleks. Rumus untuk nilai juga tidak berubah:
Notasi umum lainnya
Notasi pada nilai tidak memadai untuk membahas koefisien Fourier dari beberapa fungsi yang berbeda. Oleh karena itu, biasanya diganti dengan bentuk fungsi yang dimodifikasi (, dalam kasus ini), seperti atau , dan notasi fungsional sering menggantikan langganan:
Representasi domain frekuensi lain yang umum digunakan menggunakan koefisien deret Fourier untuk memodulasi sisir Dirac:dari mana mewakili domain frekuensi kontinu. Ketika variabel memiliki satuan detik, memiliki satuan hertz. "Gigi" sisir diberi jarak pada kelipatan (yaitu harmonik) dari nilai , yang disebut frekuensi dasar. dapat dipulihkan dari representasi ini dengan transformasi Fourier terbalik:
Fungsi yang dibangun pada nilai oleh karena itu biasanya disebut sebagai Transformasi Fourier, meskipun integral Fourier dari fungsi periodik tidak konvergen pada frekuensi harmonisa.[A]
-
Empat jumlah parsial pertama dari deret Fourier untuk gelombang persegi
Definisi
Pertimbangkan fungsi bernilai nyata, , yaitu integrable pada interval panjang , yang akan menjadi periode deret Fourier. Contoh umum interval analisis adalah:
- dan
- dan
Analisis proses menentukan bobot, diindeks dengan integer , yang merupakan jumlah siklus nilai harmonik dalam interval analisis. Oleh karena itu, panjang suatu siklus, dalam satuan , ialah . Dan frekuensi harmonik yang sesuai adalah . harmonik nilai dan , dan amplitudo (bobot) mereka ditemukan dengan integrasi selama interval panjang :[6]
Koefisien Fourier (Eq.1)
- Jika nilai ialah nilai dari nilai periodik, maka setiap interval dengan panjang tersebut sudah cukup.
- Nilai dan dapat direduksi menjadi nilai dan .
- Banyaknya teks memilih nilai untuk menyederhanakan argumen dari fungsi sinusoid.
Proses sintesis (Deret Fourier sebenarnya) adalah:
Deret Fourier, bentuk sinus-kosinus (Eq.2)
Secara umum, integer pada nilai secara teoritis tidak terbatas. Meski begitu, deretan tersebut mungkin tidak konvergen atau persis sama di semua nilai (seperti diskontinuitas satu titik) dalam interval analisis. Untuk fungsi "berperilaku baik" yang khas dari proses fisik, kesetaraan biasanya diasumsikan.

Jika adalah fungsi yang terdapat dalam interval panjang (dan nol di tempat lain), kuadran kanan atas adalah contoh dari koefisien deret Fourier Pada nilak () mungkin terlihat seperti ketika diplot terhadap frekuensi harmonik yang sesuai. Kuadran kiri atas adalah transformasi Fourier yang sesuai dari Penjumlahan deret Fourier (tidak diperlihatkan) mensintesis penjumlahan periodik sedangkan invers Fourier transform (tidak ditampilkan) hanya mensintesis Menggunakan identitas trigonometri:
dan definisi nilai dan , pasangan sinus dan kosinus dapat dinyatakan sebagai sinusoid tunggal dengan offset fase, analog dengan konversi antara koordinat ortogonal (Kartesius) dan polar:
Deret Fourier, bentuk fase amplitudo (Eq.3)
Bentuk kebiasaan untuk menggeneralisasi menjadi bernilai kompleks (bagian selanjutnya) diperoleh dengan menggunakan rumus Euler untuk membagi fungsi kosinus menjadi eksponensial kompleks. Di sini, konjugasi kompleks dilambangkan dengan tanda bintang:
Oleh karena itu, dengan definisi:
hasil akhirnya adalah:
Deret Fourier, bentuk eksponensial (Eq.4)
Konvergensi
Dalam aplikasi rekayasa, deret Fourier umumnya dianggap berkumpul hampir di semua tempat (pengecualian berada pada diskontinuitas diskrit) karena fungsi yang ditemui dalam teknik berperilaku lebih baik daripada fungsi yang dapat diberikan oleh ahli matematika sebagai contoh tandingan untuk pres ini. Secara khusus, jika kontinu dan turunan dari (yang mungkin tidak ada di semua tempat) adalah integratif persegi, kemudian deret Fourier menyatu secara mutlak dan seragam ke nilai .[7] Jika suatu fungsi adalah integral-persegi pada interval , kemudian deret Fourier menyatu dengan fungsi di hampir setiap titik. Konvergensi deret Fourier juga bergantung pada jumlah hingga maksimal dan minimal dalam suatu fungsi yang dikenal sebagai salah satu Kondisi dirichlet untuk deret Fourier. Lihat Konvergensi seri Fourier. Koefisien Fourier dapat didefinisikan untuk fungsi atau distribusi yang lebih umum, dalam kasus seperti itu konvergensi dalam norma atau konvergensi lemah biasanya berupa inte.
-
Empat jumlah parsial (deret Fourier) dengan panjang 1, 2, 3, dan 4, menunjukkan bagaimana pendekatan terhadap gelombang persegi meningkat seiring dengan bertambahnya jumlah suku (animasi)
-
Empat jumlah parsial (deret Fourier) dengan panjang 1, 2, 3, dan 4, menunjukkan bagaimana pendekatan terhadap gelombang gigi gergaji meningkat seiring dengan bertambahnya jumlah suku (animasi)
-
Contoh konvergensi ke fungsi yang agak sewenang-wenang. Perhatikan perkembangan "dering" (fenomena Gibbs) pada transisi ke / dari bagian vertikal.
Animasi interaktif dapat dilihat lihat.
Konvergen
Teorema[8]
Misalkan adalah fungsi yang periodik dengan periode , kontinu dan mulus bagian demi bagian. Maka, deret Fourier dari konvergen mutlak dan secara seragam pada .
Referensi
- ^ "Fourier". Dictionary.com Unabridged. Random House.
- ^ Dorf, Richard C.; Tallarida, Ronald J. (1993-07-15). Buku Saku Rumus Teknik Elektro (edisi ke-1). Boca Raton,FL: CRC Press. hlm. 171–174. ISBN 0849344735.
- ^ Tolstov, Georgi P. (1976). Deret Fourier. Courier-Dover. ISBN 0-486-63317-9.
- ^ a b c d Shmaliy, Y.S. (2007). Continuous-Time Signals. Springer. ISBN 1402062710.
- ^ Proakis, John G.; Manolakis, Dimitris G. (1996). Pemrosesan Sinyal Digital: Prinsip, Algoritma, dan Aplikasi
 (edisi ke-3rd). Prentice Hall. hlm. 291. ISBN 978-0-13-373762-2.
(edisi ke-3rd). Prentice Hall. hlm. 291. ISBN 978-0-13-373762-2.
- ^ Dorf, Richard C.; Tallarida, Ronald J. (1993-07-15). Buku Saku Rumus Teknik Elektro (edisi ke-1). Boca Raton,FL: CRC Press. hlm. 171–174. ISBN 0849344735.
- ^ Tolstov, Georgi P. (1976). Deret Fourier. Courier-Dover. ISBN 0-486-63317-9.
- ^ Hendra Gunawan, Catatan Kuliah Analisis Fourier dan Wavelet, 2014
Pranala luar
- Tutorial flash interaktif untuk deret Fourier
- Phasor Phactory Allows custom control of the harmonic amplitudes for arbitrary terms
- Java applet Ekspansi deret Fourier untuk fungsi sembarang
- Example problems - Contoh perhitungan deret Fourier
- Fourier series explanation - pendekatan nonmatematis sederhana
- (Inggris) Weisstein, Eric W. "Fourier Series". MathWorld.
- Modul deret Fourier oleh John H. Mathews
- Joseph Fourier Diarsipkan 2001-12-05 di Wayback Machine. - Situs web tentang riwayat Fourier historical section of this article
- SFU.ca - 'Teorema Fourier'
- In the bottom of this interactive lecture Diarsipkan 2008-12-06 di Wayback Machine., animasi Java yang menunjukkan bagaimana pengaruh terhadap deret Fourier bila suku orde ke-n+1 ditambahkan ke suku ke-n
Kesalahan pengutipan: Ditemukan tag<ref>untuk kelompok bernama "upper-alpha", tapi tidak ditemukan tag<references group="upper-alpha"/>yang berkaitan-
-



![{\displaystyle x\in [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c68354ed86bae40d711eba3ef26c4ec740fcc8fc)

![{\displaystyle x\in [-\pi ,\pi ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f68d2390bdd36e72e19b37682380f02214d52b2)






























![{\displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)
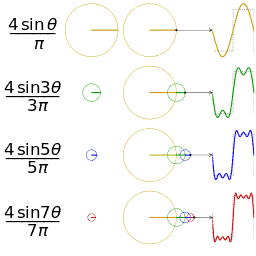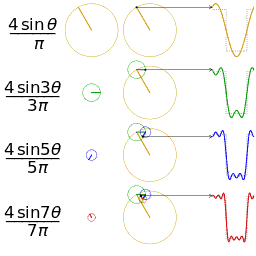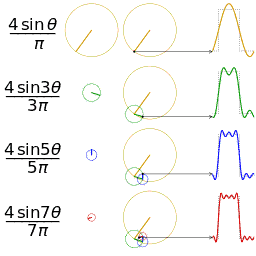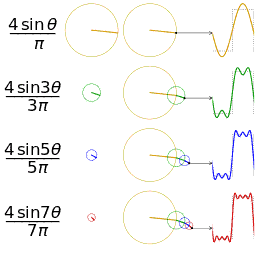



![{\displaystyle (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)



![{\displaystyle {\begin{aligned}a_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\,dx=0,\quad n\geq 0.\\[4pt]b_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\sin(nx)\,dx\\[4pt]&=-{\frac {2}{\pi n}}\cos(n\pi )+{\frac {2}{\pi ^{2}n^{2}}}\sin(n\pi )\\[4pt]&={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cd645b661c531998472837b4709b23bf2d2c939)
![{\displaystyle {\begin{aligned}s(x)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]\\[4pt]&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbb {Z} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c051045100b8d31eada1c7fcfd414759404ed25b)



![{\displaystyle (x,y)\in [0,\pi ]\times [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610)









![{\displaystyle F[n],G[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61e397cb4324837020cdcdf1d32bb9f00e3bacc3)



![{\displaystyle a\cdot F[n]+b\cdot G[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc955a6cf808d4921d875ff75eb9a0ef841fecc9)


![{\displaystyle F[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33b4a4823263d9c8be71e81b434efa1e0e7f7b78)

![{\displaystyle F[-n]^{*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a0bb8e1ac85b41420733bbc3176752128cb2ad1)

![{\displaystyle F[n]^{*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a49c30283e8c78c1a9bedb82bc10d910060b88d)

![{\displaystyle {\frac {1}{2}}(F[n]+F[-n]^{*})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/561b550cd40e3a9b9094047184114aa358f1a96b)

![{\displaystyle {\frac {1}{2i}}(F[n]-F[-n]^{*})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2317f4fc3c68ae6247b484faefb4afcfb05dfbb)

![{\displaystyle \operatorname {Re} {(F[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46139e55f1d3fefaedc2c50c143c2070a71cdb80)

![{\displaystyle \operatorname {Im} {(F[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b17cae376b2d16a948caa8532ba478bc7b78dbf)

![{\displaystyle F[n]\cdot e^{-i{\frac {2\pi x_{0}}{T}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0867072969dbc9aa6f27cca71a9ffeb6a6853a75)


![{\displaystyle F[n-n_{0}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01ff33ce94b62cdac1424cda391a7a63d678bb78)





![{\displaystyle L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)



![{\displaystyle f\in L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74d27747bf5e28fa54e94f218bd9296213ef25c5)








![{\displaystyle {\begin{aligned}c_{n}&={\frac {1}{P}}\int _{P}\operatorname {Re} \{s(x)\}\cdot e^{-i{\tfrac {2\pi nx}{P}}}\ dx+i\cdot {\frac {1}{P}}\int _{P}\operatorname {Im} \{s(x)\}\cdot e^{-i{\tfrac {2\pi nx}{P}}}\ dx\\[4pt]&={\frac {1}{P}}\int _{P}\left(\operatorname {Re} \{s(x)\}+i\cdot \operatorname {Im} \{s(x)\}\right)\cdot e^{-i{\tfrac {2\pi nx}{P}}}\ dx\ =\ {\frac {1}{P}}\int _{P}s(x)\cdot e^{-i{\tfrac {2\pi nx}{P}}}\ dx.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32ab5a1982824b357f94d5fe7410bfb84fef8e6b)

![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
![{\displaystyle {\begin{aligned}s_{\infty }(x)&=\sum _{n=-\infty }^{\infty }{\hat {s}}(n)\cdot e^{i\,2\pi nx/P}\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{j\,2\pi nx/P}&&\scriptstyle {\mathsf {common\ engineering\ notation}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a0ce35db68aa1a4984b746f18928b5d8b6eebfc)
![{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)


![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\ \ \triangleq \ s_{\infty }(x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/446316db0d563e8ceac0da5d5d078b67f0c0f4e5)