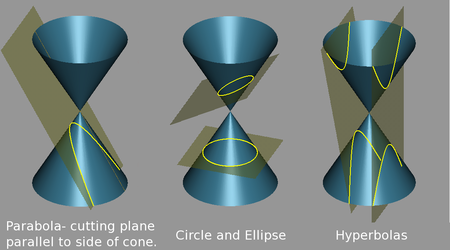
Dalam matematika , irisan kerucut adalah lokus dari semua titik yang membentuk kurva dua-dimensi , yang terbentuk oleh irisan sebuah kerucut dengan sebuah bidang . Tiga jenis kurva yang dapat terjadi adalah Parabola , Elips , dan Hiperbola . Apollonius dari Perga adalah matematikawan Yunani yang pertama mempelajari irisan kerucut secara sistematik pada awal abad ke-2 SM .
Geometri
Geometri irisan kerucut dan jenis-jenisnya Dalam memahami geometri irisan kerucut, sebuah kerucut dianggap memiliki dua kulit yang membentang sampai tak berhingga di kedua arah. Sebuah generator adalah sebuah garis yang dapat dibuat pada kulit kerucut, dan semua generator saling berpotongan di satu titik yang disebut verteks kerucut.
Jenis-jenis irisan kerucut
Jika sebuah bidang mengiris kerucut sejajar dengan satu dan hanya satu generator, maka irisannya adalah parabola . Jika bidang pengiris sejajar dengan dua generator, maka irisannya akan memotong kedua kulit dan membentuk sebuah hiperbola . Sebuah elips terjadi jika bidang pengiris tidak sejajar dengan generator mana pun. Lingkaran adalah kasus khusus dari elips, yang terbentuk jika bidang pengiris memotong semua generator dan tegak lurus sumbu kerucut.
Kasus degenerasi
Kasus-kasus degenerasi terjadi jika bidang-bidang pengiris melalui verteks kerucut. Irisan-irisannya dapat berupa titik , garis lurus, dan dua garis lurus yang saling berpotongan. Sebuah titik terjadi jika bidang pengiris melalui verteks kerucut namun tidak memotong generator mana pun. Kasus ini merupakan elips yang terdegenerasi. Jika bidang pengiris melalui verteks kerucut, dan hanya satu generator, maka yang terjadi adalah sebuah garis lurus, dan merupakan parabola yang terdegenerasi. Sebuah hiperbola terdegenerasi terjadi jika bidang pengiris melalui verteks kerucut dan dua generator sehingga memberikan dua garis lurus yang saling berpotongan.
Geometri analitis
Secara geometri analitis , irisan kerucut dapat didefinisikan sebagai:
tempat kedudukan titik-titik pada sebuah bidang, sedemikian, sehingga jarak titik-titik tersebut ke sebuah titik tetap F (yang disebut fokus) memiliki rasio yang konstan terhadap jarak titik-titik tersebut ke sebuah garis tetap L (disebut direktriks) yang tidak mengandung F[ 1]
Eksentrisitas adalah rasio antara FM dan M'M . Elips (e =1/2) , parabola (e =1) dan hiperbola (e =2) dengan fokus (F ) dan direktriks yang tetap. Rasio yang konstan tersebut disebut eksentrisitas , dilambangkan dengan e , dan merupakan bilangan non-negatif. Untuk e = 0, irisan kerucut tersebut adalah lingkaran, 0 < e < 1 sebuah elips, e = 1 sebuah parabola, dan e > 1 sebuah hiperbola.
Koordinat Kartesius
Dalam koordinat kartesius , grafik dari persamaan kuadrat dengan dua variabel selalu menghasilkan irisan kerucut, dan semua irisan kerucut dapat dihasilkan dengan cara ini.
Jika terdapat persamaan dengan bentuk:
a
x
2
+
2
h
x
y
+
b
y
2
+
2
g
x
+
2
f
y
+
c
=
0
{\displaystyle ax^{2}+2hxy+by^{2}+2gx+2fy+c=0}
maka:
Jika h2 = ab , persamaan ini menghasilkan parabola .
Jika h2 < ab , persamaan ini menghasilkan elips .
Jika h2 > ab , persamaan ini menghasilkan hiperbola .
Jika a = b dan h = 0, persamaan ini menghasilkan lingkaran .
Jika a + b = 0, persamaan ini menghasilkan hiperbola persegi.
Bentuk persamaan umum
Bentuk persamaan umum sebagai berikut:
A
x
2
+
B
x
y
+
C
y
2
+
D
x
+
E
y
+
F
=
0
{\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0}
]
kesimpulan:
Jika A = B = 0 maka persamaan adalah garis lurus /linear
Jika A = B = 0 tetapi tidak kedua-duanya maka persamaan adalah parabola /kuadrat
Jika A = B maka persamaan adalah lingkaran
Jika A ≠ B dan bertanda positif maka persamaan adalah elips
Jika A ≠ B dan bertanda negatif maka persamaan adalah hiperbola
Sekilas irisan kerucut
Lingkaran
Titik pusat (0,0):
x
2
+
y
2
=
r
2
{\displaystyle x^{2}+y^{2}=r^{2}}
Titik pusat (h,k):
(
x
−
h
)
2
+
(
y
−
k
)
2
=
r
2
{\displaystyle (x-h)^{2}+(y-k)^{2}=r^{2}}
x
2
+
2
h
x
+
h
2
+
y
2
+
2
k
y
+
k
2
−
r
2
=
0
{\displaystyle x^{2}+2hx+h^{2}+y^{2}+2ky+k^{2}-r^{2}=0}
dengan
x
2
+
y
2
+
A
x
+
B
y
+
C
=
0
{\displaystyle x^{2}+y^{2}+Ax+By+C=0}
A
=
2
h
,
B
=
2
k
s
e
r
t
a
C
=
h
2
+
k
2
−
r
2
{\displaystyle A=2h,B=2ksertaC=h^{2}+k^{2}-r^{2}}
Parabola
Vertikal
Horisontal
Titik pusat (0,0)
Persamaan
x
2
=
4
p
y
{\displaystyle x^{2}=4py}
y
2
=
4
p
x
{\displaystyle y^{2}=4px}
Sumbu simetri
sumbu y
sumbu x
Fokus
F
(
0
,
p
)
{\displaystyle F(0,p)}
F
(
p
,
0
)
{\displaystyle F(p,0)}
Direktris
y
=
−
p
{\displaystyle y=-p}
x
=
−
p
{\displaystyle x=-p}
Titik pusat (h,k)
Persamaan
(
x
−
h
)
2
=
4
p
(
y
−
k
)
{\displaystyle (x-h)^{2}=4p(y-k)}
(
y
−
k
)
2
=
4
p
(
x
−
h
)
{\displaystyle (y-k)^{2}=4p(x-h)}
Sumbu simetri
x
=
h
{\displaystyle x=h}
y
=
k
{\displaystyle y=k}
Fokus
F
(
h
,
k
+
p
)
{\displaystyle F(h,k+p)}
F
(
h
+
p
,
k
)
{\displaystyle F(h+p,k)}
Direktris
y
=
k
−
p
{\displaystyle y=k-p}
x
=
h
−
p
{\displaystyle x=h-p}
Elips
Vertikal
Horisontal
Titik pusat (0,0)
Persamaan
x
2
b
2
+
y
2
a
2
=
1
{\displaystyle {\frac {x^{2}}{b^{2}}}+{\frac {y^{2}}{a^{2}}}=1}
x
2
a
2
+
y
2
b
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}
Panjang sumbu mayor
2
a
{\displaystyle 2a}
2
a
{\displaystyle 2a}
Panjang sumbu minor
2
b
{\displaystyle 2b}
2
b
{\displaystyle 2b}
Panjang Latus Rectum
L
=
2
b
2
a
{\displaystyle L={\frac {2b^{2}}{a}}}
L
=
2
b
2
a
{\displaystyle L={\frac {2b^{2}}{a}}}
Fokus
F
(
0
,
±
c
)
{\displaystyle F(0,\pm c)}
F
(
±
c
,
0
)
{\displaystyle F(\pm c,0)}
Puncak
P
(
0
,
±
a
)
{\displaystyle P(0,\pm a)}
P
(
±
a
,
0
)
{\displaystyle P(\pm a,0)}
Direktris
y
=
±
a
2
c
{\displaystyle y=\pm {\frac {a^{2}}{c}}}
x
=
±
a
2
c
{\displaystyle x=\pm {\frac {a^{2}}{c}}}
Eksentrisitas
e
=
c
a
{\displaystyle e={\frac {c}{a}}}
e
=
c
a
{\displaystyle e={\frac {c}{a}}}
Titik pusat (h,k)
Persamaan
(
x
−
h
)
2
b
2
+
(
y
−
k
)
2
a
2
=
1
{\displaystyle {\frac {(x-h)^{2}}{b^{2}}}+{\frac {(y-k)^{2}}{a^{2}}}=1}
(
x
−
h
)
2
a
2
+
(
y
−
k
)
2
b
2
=
1
{\displaystyle {\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}{b^{2}}}=1}
Panjang sumbu mayor
2
a
{\displaystyle 2a}
2
a
{\displaystyle 2a}
Panjang sumbu minor
2
b
{\displaystyle 2b}
2
b
{\displaystyle 2b}
Panjang Latus Rectum
L
=
2
b
2
a
{\displaystyle L={\frac {2b^{2}}{a}}}
L
=
2
b
2
a
{\displaystyle L={\frac {2b^{2}}{a}}}
Fokus
F
(
h
,
k
±
c
)
{\displaystyle F(h,k\pm c)}
F
(
h
±
c
,
k
)
{\displaystyle F(h\pm c,k)}
Puncak
P
(
h
,
k
±
a
)
{\displaystyle P(h,k\pm a)}
P
(
h
±
a
,
k
)
{\displaystyle P(h\pm a,k)}
Direktris
y
=
±
a
2
c
{\displaystyle y=\pm {\frac {a^{2}}{c}}}
x
=
±
a
2
c
{\displaystyle x=\pm {\frac {a^{2}}{c}}}
Eksentrisitas
e
=
c
a
{\displaystyle e={\frac {c}{a}}}
e
=
c
a
{\displaystyle e={\frac {c}{a}}}
dimana
c
=
a
2
−
b
2
{\displaystyle c={\sqrt {a^{2}-b^{2}}}}
Hiperbola
Vertikal
Horisontal
Titik pusat (0,0)
Persamaan
x
2
b
2
−
y
2
a
2
=
1
{\displaystyle {\frac {x^{2}}{b^{2}}}-{\frac {y^{2}}{a^{2}}}=1}
x
2
a
2
−
y
2
b
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}
Panjang sumbu mayor
2
a
{\displaystyle 2a}
2
a
{\displaystyle 2a}
Panjang sumbu minor
2
b
{\displaystyle 2b}
2
b
{\displaystyle 2b}
Panjang Latus Rectum
L
=
2
b
2
a
{\displaystyle L={\frac {2b^{2}}{a}}}
L
=
2
b
2
a
{\displaystyle L={\frac {2b^{2}}{a}}}
Fokus
F
(
0
,
±
c
)
{\displaystyle F(0,\pm c)}
F
(
±
c
,
0
)
{\displaystyle F(\pm c,0)}
Puncak
P
(
0
,
±
a
)
{\displaystyle P(0,\pm a)}
P
(
±
a
,
0
)
{\displaystyle P(\pm a,0)}
Asimtot
y
=
±
a
b
x
{\displaystyle y=\pm {\frac {a}{b}}x}
y
=
±
b
a
x
{\displaystyle y=\pm {\frac {b}{a}}x}
Eksentrisitas
e
=
c
a
{\displaystyle e={\frac {c}{a}}}
e
=
c
a
{\displaystyle e={\frac {c}{a}}}
Titik pusat (h,k)
Persamaan
(
x
−
h
)
2
b
2
−
(
y
−
k
)
2
a
2
=
1
{\displaystyle {\frac {(x-h)^{2}}{b^{2}}}-{\frac {(y-k)^{2}}{a^{2}}}=1}
(
x
−
h
)
2
a
2
−
(
y
−
k
)
2
b
2
=
1
{\displaystyle {\frac {(x-h)^{2}}{a^{2}}}-{\frac {(y-k)^{2}}{b^{2}}}=1}
Panjang sumbu mayor
2
a
{\displaystyle 2a}
2
a
{\displaystyle 2a}
Panjang sumbu minor
2
b
{\displaystyle 2b}
2
b
{\displaystyle 2b}
Panjang Latus Rectum
L
=
2
b
2
a
{\displaystyle L={\frac {2b^{2}}{a}}}
L
=
2
b
2
a
{\displaystyle L={\frac {2b^{2}}{a}}}
Fokus
F
(
h
,
k
±
c
)
{\displaystyle F(h,k\pm c)}
F
(
h
±
c
,
k
)
{\displaystyle F(h\pm c,k)}
Puncak
P
(
h
,
k
±
a
)
{\displaystyle P(h,k\pm a)}
P
(
h
±
a
,
k
)
{\displaystyle P(h\pm a,k)}
Asimtot
(
y
−
k
)
=
±
a
b
(
x
−
h
)
{\displaystyle (y-k)=\pm {\frac {a}{b}}(x-h)}
(
y
−
k
)
=
±
b
a
(
x
−
h
)
{\displaystyle (y-k)=\pm {\frac {b}{a}}(x-h)}
Eksentrisitas
e
=
c
a
{\displaystyle e={\frac {c}{a}}}
e
=
c
a
{\displaystyle e={\frac {c}{a}}}
dimana
c
=
a
2
+
b
2
{\displaystyle c={\sqrt {a^{2}+b^{2}}}}
Persamaan garis singgung
bergradien
m
{\displaystyle m}
y
=
m
x
+
c
{\displaystyle y=mx+c}
Vertikal
Horisontal
Titik pusat (0,0)
Lingkaran
y
=
m
x
±
r
1
+
m
2
{\displaystyle y=mx\pm r{\sqrt {1+m^{2}}}}
Parabala
y
=
m
x
−
p
m
{\displaystyle y=mx-pm}
y
=
m
x
+
p
m
{\displaystyle y=mx+{\frac {p}{m}}}
Elips
y
=
m
x
±
b
2
+
a
2
m
2
{\displaystyle y=mx\pm {\sqrt {b^{2}+a^{2}m^{2}}}}
y
=
m
x
±
a
2
m
2
+
b
2
{\displaystyle y=mx\pm {\sqrt {a^{2}m^{2}+b^{2}}}}
Hiperbola
y
=
m
x
±
b
2
−
a
2
m
2
{\displaystyle y=mx\pm {\sqrt {b^{2}-a^{2}m^{2}}}}
y
=
m
x
±
a
2
m
2
−
b
2
{\displaystyle y=mx\pm {\sqrt {a^{2}m^{2}-b^{2}}}}
Titik pusat (h,k)
Lingkaran
(
y
−
k
)
=
m
(
x
−
h
)
±
r
1
+
m
{\displaystyle (y-k)=m(x-h)\pm r{\sqrt {1+m}}}
Parabala
(
y
−
k
)
=
m
(
x
−
h
)
−
p
m
{\displaystyle (y-k)=m(x-h)-pm}
(
y
−
k
)
=
m
(
x
−
h
)
+
p
m
{\displaystyle (y-k)=m(x-h)+{\frac {p}{m}}}
Elips
(
y
−
k
)
=
m
(
x
−
h
)
±
b
2
+
a
2
m
2
{\displaystyle (y-k)=m(x-h)\pm {\sqrt {b^{2}+a^{2}m^{2}}}}
(
y
−
k
)
=
m
(
x
−
h
)
±
a
2
m
2
+
b
2
{\displaystyle (y-k)=m(x-h)\pm {\sqrt {a^{2}m^{2}+b^{2}}}}
Hiperbola
y
=
m
x
±
b
2
−
a
2
m
2
{\displaystyle y=mx\pm {\sqrt {b^{2}-a^{2}m^{2}}}}
y
=
m
x
±
a
2
m
2
−
b
2
{\displaystyle y=mx\pm {\sqrt {a^{2}m^{2}-b^{2}}}}
jika persamaan garis lurus bergradien sejajar maka
m
2
=
m
1
{\displaystyle m_{2}=m_{1}}
jika persamaan garis lurus bergradien tegak lurus maka
m
2
=
−
1
m
1
{\displaystyle m_{2}={\frac {-1}{m_{1}}}}
melalui titik
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
dengan cara bagi adil
Vertikal
Horisontal
Titik pusat (0,0)
Lingkaran
x
x
1
+
y
y
1
=
r
2
{\displaystyle xx_{1}+yy_{1}=r^{2}}
Parabola
x
x
1
=
2
p
y
+
2
p
y
1
{\displaystyle xx_{1}=2py+2py_{1}}
y
y
1
=
2
p
x
+
2
p
x
1
{\displaystyle yy_{1}=2px+2px_{1}}
Elips
x
x
1
b
2
+
y
y
1
a
2
=
1
{\displaystyle {\frac {xx_{1}}{b^{2}}}+{\frac {yy_{1}}{a^{2}}}=1}
x
x
1
a
2
+
y
y
1
b
2
=
1
{\displaystyle {\frac {xx_{1}}{a^{2}}}+{\frac {yy_{1}}{b^{2}}}=1}
Hiperbola
x
x
1
b
2
−
y
y
1
a
2
=
1
{\displaystyle {\frac {xx_{1}}{b^{2}}}-{\frac {yy_{1}}{a^{2}}}=1}
x
x
1
a
2
−
y
y
1
b
2
=
1
{\displaystyle {\frac {xx_{1}}{a^{2}}}-{\frac {yy_{1}}{b^{2}}}=1}
Titik pusat (h,k)
Lingkaran
(
x
−
h
)
(
x
1
−
h
)
+
(
y
−
k
)
(
y
1
−
k
)
=
r
2
{\displaystyle (x-h)(x_{1}-h)+(y-k)(y_{1}-k)=r^{2}}
x
x
1
+
y
y
1
+
1
2
A
x
+
1
2
A
x
1
+
1
2
B
y
+
1
2
B
y
1
+
C
=
0
{\displaystyle xx_{1}+yy_{1}+{\frac {1}{2}}Ax+{\frac {1}{2}}Ax_{1}+{\frac {1}{2}}By+{\frac {1}{2}}By_{1}+C=0}
Parabola
(
x
−
h
)
(
x
1
−
h
)
=
2
p
(
y
−
k
)
+
2
p
(
y
1
−
k
)
{\displaystyle (x-h)(x_{1}-h)=2p(y-k)+2p(y_{1}-k)}
(
y
−
k
)
(
y
1
−
k
)
=
2
p
(
x
−
h
)
+
2
p
(
x
1
−
h
)
{\displaystyle (y-k)(y_{1}-k)=2p(x-h)+2p(x_{1}-h)}
Elips
(
x
−
h
)
(
x
1
−
h
)
b
2
+
(
y
−
k
)
(
y
1
−
k
)
a
2
=
1
{\displaystyle {\frac {(x-h)(x_{1}-h)}{b^{2}}}+{\frac {(y-k)(y_{1}-k)}{a^{2}}}=1}
(
x
−
h
)
(
x
1
−
h
)
a
2
+
(
y
−
k
)
(
y
1
−
k
)
b
2
=
1
{\displaystyle {\frac {(x-h)(x_{1}-h)}{a^{2}}}+{\frac {(y-k)(y_{1}-k)}{b^{2}}}=1}
Hiperbola
(
x
−
h
)
(
x
1
−
h
)
b
2
−
(
y
−
k
)
(
y
1
−
k
)
a
2
=
1
{\displaystyle {\frac {(x-h)(x_{1}-h)}{b^{2}}}-{\frac {(y-k)(y_{1}-k)}{a^{2}}}=1}
(
x
−
h
)
(
x
1
−
h
)
a
2
−
(
y
−
k
)
(
y
1
−
k
)
b
2
=
1
{\displaystyle {\frac {(x-h)(x_{1}-h)}{a^{2}}}-{\frac {(y-k)(y_{1}-k)}{b^{2}}}=1}
jika titik
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
jika titik
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
Contoh:
Titik pusat (0,0) Tentukan persamaan garis singgung yang bergradien 2 terhadap
y
2
=
16
x
{\displaystyle y^{2}=16x}
jawab:
y
2
=
16
x
−
>
y
2
=
4
(
4
x
)
j
a
d
i
p
=
4
{\displaystyle y^{2}=16x->y^{2}=4(4x)jadip=4}
y
=
2
x
+
4
2
−
>
y
=
2
x
+
2
{\displaystyle y=2x+{\frac {4}{2}}->y=2x+2}
Tentukan persamaan garis singgung yang melalui (4,8) terhadap
y
2
=
16
x
{\displaystyle y^{2}=16x}
jawab:
y
2
−
16
x
=
0
m
a
k
a
m
a
s
u
k
k
a
n
l
a
h
(
4
,
8
)
(
8
)
2
−
16
(
4
)
=
0
=
0
{\displaystyle y^{2}-16x=0makamasukkanlah(4,8)(8)^{2}-16(4)=0=0}
dengan cara bagi adil
y
y
1
=
2
p
x
+
2
p
x
1
{\displaystyle yy_{1}=2px+2px_{1}}
8
y
=
8
x
+
8
(
4
)
{\displaystyle 8y=8x+8(4)}
8
y
=
8
x
+
32
{\displaystyle 8y=8x+32}
y
=
x
+
4
{\displaystyle y=x+4}
Tentukan persamaan garis singgung yang melalui (1,5) terhadap
y
2
=
16
x
{\displaystyle y^{2}=16x}
jawab:
y
2
−
16
x
=
0
m
a
k
a
m
a
s
u
k
k
a
n
l
a
h
(
1
,
5
)
(
5
)
2
−
16
(
1
)
=
9
>
0
{\displaystyle y^{2}-16x=0makamasukkanlah(1,5)(5)^{2}-16(1)=9>0}
dengan cara bagi adil
y
y
1
=
2
p
x
+
2
p
x
1
{\displaystyle yy_{1}=2px+2px_{1}}
5
y
=
8
x
+
8
(
1
)
{\displaystyle 5y=8x+8(1)}
5
y
=
8
x
+
8
{\displaystyle 5y=8x+8}
y
=
8
5
x
+
8
5
{\displaystyle y={\frac {8}{5}}x+{\frac {8}{5}}}
masukkan lah
y
2
=
16
x
{\displaystyle y^{2}=16x}
(
8
5
x
+
8
5
)
2
=
16
x
{\displaystyle ({\frac {8}{5}}x+{\frac {8}{5}})^{2}=16x}
64
25
x
2
+
128
25
x
+
64
25
−
16
x
=
0
{\displaystyle {\frac {64}{25}}x^{2}+{\frac {128}{25}}x+{\frac {64}{25}}-16x=0}
64
25
x
2
+
128
25
x
+
64
25
−
400
25
x
=
0
{\displaystyle {\frac {64}{25}}x^{2}+{\frac {128}{25}}x+{\frac {64}{25}}-{\frac {400}{25}}x=0}
64
25
x
2
−
272
25
x
+
64
25
=
0
{\displaystyle {\frac {64}{25}}x^{2}-{\frac {272}{25}}x+{\frac {64}{25}}=0}
4
x
2
−
17
x
+
4
=
0
{\displaystyle 4x^{2}-17x+4=0}
maka kita mencari nilai x
x
=
−
b
±
b
2
−
4
a
c
2
a
{\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}
x
=
17
±
289
−
256
8
{\displaystyle x={\frac {17\pm {\sqrt {289-256}}}{8}}}
x
=
17
±
33
8
{\displaystyle x={\frac {17\pm {\sqrt {33}}}{8}}}
x
1
=
17
+
33
8
{\displaystyle x_{1}={\frac {17+{\sqrt {33}}}{8}}}
x
2
=
17
−
33
8
{\displaystyle x_{2}={\frac {17-{\sqrt {33}}}{8}}}
maka kita mencari nilai y
untuk
x
1
{\displaystyle x_{1}}
y
1
=
8
5
(
17
+
33
8
)
+
8
5
{\displaystyle y_{1}={\frac {8}{5}}({\frac {17+{\sqrt {33}}}{8}})+{\frac {8}{5}}}
y
1
=
17
5
+
33
5
+
8
5
{\displaystyle y_{1}={\frac {17}{5}}+{\frac {\sqrt {33}}{5}}+{\frac {8}{5}}}
y
1
=
5
+
33
5
{\displaystyle y_{1}=5+{\frac {\sqrt {33}}{5}}}
jadi
(
17
+
33
8
,
5
+
33
5
)
{\displaystyle ({\frac {17+{\sqrt {33}}}{8}},5+{\frac {\sqrt {33}}{5}})}
untuk
x
2
{\displaystyle x_{2}}
y
2
=
8
5
(
17
−
33
8
)
+
8
5
{\displaystyle y_{2}={\frac {8}{5}}({\frac {17-{\sqrt {33}}}{8}})+{\frac {8}{5}}}
y
2
=
17
5
−
33
5
+
8
5
{\displaystyle y_{2}={\frac {17}{5}}-{\frac {\sqrt {33}}{5}}+{\frac {8}{5}}}
y
2
=
5
−
33
5
{\displaystyle y_{2}=5-{\frac {\sqrt {33}}{5}}}
jadi
(
17
−
33
8
,
5
−
33
5
)
{\displaystyle ({\frac {17-{\sqrt {33}}}{8}},5-{\frac {\sqrt {33}}{5}})}
kembali dengan cara bagi adil
untuk persamaan singgung pertama
y
y
1
=
2
p
x
+
2
p
x
1
{\displaystyle yy_{1}=2px+2px_{1}}
(
5
+
33
5
)
y
=
8
x
+
8
(
17
+
33
8
)
{\displaystyle (5+{\frac {\sqrt {33}}{5}})y=8x+8({\frac {17+{\sqrt {33}}}{8}})}
(
5
+
33
5
)
y
=
8
x
+
17
+
33
{\displaystyle (5+{\frac {\sqrt {33}}{5}})y=8x+17+{\sqrt {33}}}
untuk persamaan singgung kedua
y
y
2
=
2
p
x
+
2
p
x
2
{\displaystyle yy_{2}=2px+2px_{2}}
(
5
−
33
5
)
y
=
8
x
+
8
(
17
−
33
8
)
{\displaystyle (5-{\frac {\sqrt {33}}{5}})y=8x+8({\frac {17-{\sqrt {33}}}{8}})}
(
5
−
33
5
)
y
=
8
x
+
17
−
33
{\displaystyle (5-{\frac {\sqrt {33}}{5}})y=8x+17-{\sqrt {33}}}
Titik pusat (h,k) Tentukan persamaan garis singgung
y
2
−
6
y
−
8
x
+
9
=
0
{\displaystyle y^{2}-6y-8x+9=0}
y
−
2
x
−
5
=
0
{\displaystyle y-2x-5=0}
jawab:
ubah ke bentuk sederhana
y
2
−
6
y
−
8
x
+
9
=
0
{\displaystyle y^{2}-6y-8x+9=0}
y
2
−
6
y
+
9
=
8
x
{\displaystyle y^{2}-6y+9=8x}
(
y
−
3
)
2
=
8
x
{\displaystyle (y-3)^{2}=8x}
cari gradien persamaan
y
−
2
x
−
5
=
0
{\displaystyle y-2x-5=0}
y
−
2
x
−
5
=
0
{\displaystyle y-2x-5=0}
y
=
2
x
+
5
{\displaystyle y=2x+5}
gradien (
m
1
{\displaystyle m_{1}}
m
2
=
−
1
2
{\displaystyle m_{2}=-{\frac {1}{2}}}
cari
p
{\displaystyle p}
(
y
−
3
)
2
=
8
x
−
>
(
y
−
3
)
2
=
4
(
2
x
)
j
a
d
i
p
=
2
{\displaystyle (y-3)^{2}=8x->(y-3)^{2}=4(2x)jadip=2}
y
=
−
1
2
x
+
2
−
1
2
−
>
y
=
−
1
2
x
−
4
{\displaystyle y=-{\frac {1}{2}}x+{\frac {2}{-{\frac {1}{2}}}}->y=-{\frac {1}{2}}x-4}
Tentukan persamaan garis singgung
y
2
−
6
y
−
8
x
+
9
=
0
{\displaystyle y^{2}-6y-8x+9=0}
jawab:
ubah ke bentuk sederhana
y
2
−
6
y
−
8
x
+
9
=
0
{\displaystyle y^{2}-6y-8x+9=0}
y
2
−
6
y
+
9
=
8
x
{\displaystyle y^{2}-6y+9=8x}
(
y
−
3
)
2
=
8
x
{\displaystyle (y-3)^{2}=8x}
cari absis dimana ordinat 6
(
6
−
3
)
2
=
8
x
{\displaystyle (6-3)^{2}=8x}
9
=
8
x
{\displaystyle 9=8x}
x
=
9
8
{\displaystyle x={\frac {9}{8}}}
dengan cara bagi adil
(
y
−
k
)
(
y
1
−
k
)
=
2
p
x
+
2
p
x
1
{\displaystyle (y-k)(y_{1}-k)=2px+2px_{1}}
(
y
−
3
)
(
6
−
3
)
=
4
x
+
4
(
9
8
)
{\displaystyle (y-3)(6-3)=4x+4({\frac {9}{8}})}
(
y
−
3
)
3
=
4
x
+
9
2
{\displaystyle (y-3)3=4x+{\frac {9}{2}}}
3
y
−
9
=
4
x
+
9
2
{\displaystyle 3y-9=4x+{\frac {9}{2}}}
3
y
=
4
x
+
27
2
{\displaystyle 3y=4x+{\frac {27}{2}}}
y
=
4
3
x
+
27
6
{\displaystyle y={\frac {4}{3}}x+{\frac {27}{6}}}
Tentukan persamaan garis singgung yang melalui (1,6) terhadap
y
2
−
6
y
−
8
x
+
9
=
0
{\displaystyle y^{2}-6y-8x+9=0}
ubah ke bentuk sederhana
y
2
−
6
y
−
8
x
+
9
=
0
{\displaystyle y^{2}-6y-8x+9=0}
y
2
−
6
y
+
9
=
8
x
{\displaystyle y^{2}-6y+9=8x}
(
y
−
3
)
2
=
8
x
{\displaystyle (y-3)^{2}=8x}
(
y
−
3
)
2
−
8
x
=
0
m
a
k
a
m
a
s
u
k
k
a
n
l
a
h
(
1
,
6
)
(
6
−
3
)
2
−
8
(
1
)
=
9
−
8
=
1
>
0
{\displaystyle (y-3)^{2}-8x=0makamasukkanlah(1,6)(6-3)^{2}-8(1)=9-8=1>0}
dengan cara bagi adil
(
y
−
k
)
(
y
1
−
k
)
=
2
p
x
+
2
p
x
1
{\displaystyle (y-k)(y_{1}-k)=2px+2px_{1}}
(
y
−
3
)
(
6
−
3
)
=
4
x
+
4
(
1
)
{\displaystyle (y-3)(6-3)=4x+4(1)}
(
y
−
3
)
3
=
4
x
+
4
{\displaystyle (y-3)3=4x+4}
3
y
−
9
=
4
x
+
4
{\displaystyle 3y-9=4x+4}
3
y
=
4
x
+
13
{\displaystyle 3y=4x+13}
y
=
4
3
x
+
13
3
{\displaystyle y={\frac {4}{3}}x+{\frac {13}{3}}}
masukkan lah
(
y
−
3
)
2
=
8
x
{\displaystyle (y-3)^{2}=8x}
(
4
3
x
+
13
3
−
3
)
2
=
8
x
{\displaystyle ({\frac {4}{3}}x+{\frac {13}{3}}-3)^{2}=8x}
(
4
3
x
+
4
3
)
2
=
8
x
{\displaystyle ({\frac {4}{3}}x+{\frac {4}{3}})^{2}=8x}
16
9
x
2
+
32
9
x
+
16
9
−
8
x
=
0
{\displaystyle {\frac {16}{9}}x^{2}+{\frac {32}{9}}x+{\frac {16}{9}}-8x=0}
16
9
x
2
−
40
9
x
+
16
9
=
0
{\displaystyle {\frac {16}{9}}x^{2}-{\frac {40}{9}}x+{\frac {16}{9}}=0}
2
x
2
+
5
x
+
2
=
0
{\displaystyle 2x^{2}+5x+2=0}
maka kita mencari nilai x
x
=
−
b
±
b
2
−
4
a
c
2
a
{\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}
x
=
5
±
25
−
16
4
{\displaystyle x={\frac {5\pm {\sqrt {25-16}}}{4}}}
x
=
5
±
9
4
{\displaystyle x={\frac {5\pm {\sqrt {9}}}{4}}}
x
1
=
5
+
9
4
=
2
{\displaystyle x_{1}={\frac {5+{\sqrt {9}}}{4}}=2}
x
2
=
5
−
9
4
=
1
2
{\displaystyle x_{2}={\frac {5-{\sqrt {9}}}{4}}={\frac {1}{2}}}
maka kita mencari nilai y
untuk
x
1
{\displaystyle x_{1}}
y
1
=
4
3
(
2
)
+
13
3
=
8
3
+
13
3
=
7
{\displaystyle y_{1}={\frac {4}{3}}(2)+{\frac {13}{3}}={\frac {8}{3}}+{\frac {13}{3}}=7}
jadi
(
2
,
7
)
{\displaystyle (2,7)}
untuk
x
2
{\displaystyle x_{2}}
y
2
=
4
3
(
1
2
)
+
13
3
=
2
3
+
13
3
=
5
{\displaystyle y_{2}={\frac {4}{3}}({\frac {1}{2}})+{\frac {13}{3}}={\frac {2}{3}}+{\frac {13}{3}}=5}
jadi
(
1
2
,
5
)
{\displaystyle ({\frac {1}{2}},5)}
kembali dengan cara bagi adil
untuk persamaan singgung pertama
(
y
−
k
)
(
y
1
−
k
)
=
2
p
x
+
2
p
x
1
{\displaystyle (y-k)(y_{1}-k)=2px+2px_{1}}
(
y
−
3
)
(
7
−
3
)
=
4
x
+
4
(
2
)
{\displaystyle (y-3)(7-3)=4x+4(2)}
(
y
−
3
)
4
=
4
x
+
8
{\displaystyle (y-3)4=4x+8}
4
y
−
12
=
4
x
+
8
{\displaystyle 4y-12=4x+8}
4
y
=
4
x
+
20
{\displaystyle 4y=4x+20}
y
=
x
+
5
{\displaystyle y=x+5}
untuk persamaan singgung kedua
(
y
−
k
)
(
y
2
−
k
)
=
2
p
x
+
2
p
x
2
{\displaystyle (y-k)(y_{2}-k)=2px+2px_{2}}
(
y
−
3
)
(
5
−
3
)
=
4
x
+
4
(
1
2
)
{\displaystyle (y-3)(5-3)=4x+4({\frac {1}{2}})}
(
y
−
3
)
2
=
4
x
+
2
{\displaystyle (y-3)2=4x+2}
2
y
−
6
=
4
x
+
2
{\displaystyle 2y-6=4x+2}
2
y
=
4
x
+
8
{\displaystyle 2y=4x+8}
y
=
2
x
+
4
{\displaystyle y=2x+4}
Referensi
^ Leithold, Louis (1981). "13". The Calculus with Analytic Geometry . New York: Harper & Row, Publisher, Inc. hlm. 657. ISBN 0-06-043935-1 .