Frustum

Frustum
Contoh: Frustum pentagonal dan persegi siku-siku (n=5 dan n=4)
Muka	$n$ trapesium sama kaki, 2 poligon beraturan
Rusuk	$3n$
titik sudut	$2n$
Polihedron dual	bipiramida segi-$n$ siku-siku asimetrik cembung
Sifat-sifat	cembung

Dalam geometri, frustum adalah suatu bagian dari bangun ruang seperti kerucut atau limas, yang terletak di antara dua bidang sejajar yang memotongnya. Dalam kasus limas, muka alas berupa poligon, dan muka sisi berupa trapesium. Frustum siku-siku adalah limas siku-siku atau kerucut siku-siku terpenggal, yang tegak lurus dengan garis sumbunya. Pemenggalan bangunan tersebut yang bukan siku-siku disebut frustum bukan siku-siku.

Rumus

Volume

Rumus volume frustum persegi piramida diperkenalkan oleh matematika Mesir kuno, yang dikenal sebagai Moskow Matematika Papirus. yang ditulis pada dinasti ke-13 (sekitar 1850 SM):$$V={\frac {h}{3}}(a^{2}+ab+b^{2}).$$dengan $a$ dan $b$ masing-masing menyatakan panjang alas dan panjang sisi di atas, serta $h$ menyatakan tinggi. Orang Mesir mengetahui rumus yang tepat untuk volume piramida persegi penggal, tetapi belum ada bukti dari persamaan tersebut dalam papirus Moskow.

Volume frustum kerucut atau limas merupakan volume bangun ruang sebelum mengiris bagian puncaknya, yang kemudian dikurangi volume bagian puncak:$$V={\frac {h_{1}B_{1}-h_{2}B_{2}}{3}}$$dengan $B_{1}$menyatakan luas alas, dan $B_{2}$ menyatakan luas sisi di bagian atas frustum; serta $h_{1}$menyatakan garis tinggi yang tegak lurus dari titik puncak ke alas, dan $h_{2}$ menyatakan garis tinggi yang tegak lurus dari titik puncak ke sisi di bagian atas frustum.

Mengingat bahwa

${\frac {B_{1}}{t_{1}^{2}}}={\frac {B_{2}}{t_{2}^{2}}}={\frac {\sqrt {B_{1}B_{2}}}{t_{1}t_{2}}}=\alpha$,

rumus untuk volume dapat dinyatakan sebagai produk proporsionalitas ini α/3 dan perbedaan kubus dengan ketinggian t1 dan t2 saja.

$V={\frac {t_{1}\alpha t_{1}^{2}-t_{2}\alpha t_{2}^{2}}{3}}={\frac {\alpha }{3}}(t_{1}^{3}-t_{2}^{3})$

Dengan memfaktorkan perbedaan dua kubus $(a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2}))$ seseorang mendapat t1-t2 = t, ketinggian frustum, dan $\alpha \times {\frac {(t_{1}^{2}+t_{1}t_{2}+t_{2}^{2})}{3}}$.

Mendistribusikan α dan menggantikannya dari definisinya, rata Heronian dari daerah B1 dan B2 diperoleh. Karena itu, formula alternatifnya

$V={\frac {t}{3}}(B_{1}+{\sqrt {B_{1}B_{2}}}+B_{2})$.

Bangau Aleksandria terkenal karena menurunkan formula ini dan dengan itu berhadapan dengan bilangan imajiner, akar kuadrat dari bilangan negatif.

Secara khusus, volume frustum kerucut melingkar adalah

$V={\frac {\pi t}{3}}(r_{1}^{2}+r_{1}r_{2}+r_{2}^{2})$

di mana π adalah 3.14159265 ..., dan r1, r2 adalah jari - jari kedua pangkalan.

Volume dari suatu piramidal frustum yang basisnya adalah n- sisi [volume polihedron sisi-n] adalah poligon reguler

$V={\frac {nt}{12}}(a_{1}^{2}+a_{1}a_{2}+a_{2}^{2})\cot {\frac {\pi }{n}}$

Luas selimut

Frustum kerucut

Model 3D dari frustum melingkar.

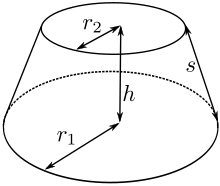
Untuk frustum berbentuk kerucut melingkar kanan

${\begin{aligned}L=\pi (r_{1}+r_{2})s=\pi (r_{1}+r_{2}){\sqrt {(r_{1}-r_{2})^{2}+t^{2}}}\end{aligned}}$

Luas permukaan

$L=L_{ab}+L_{ab}+L_{s}$

${\begin{aligned}L=\pi (r_{1}^{2}+r_{2}^{2}+(r_{1}+r_{2})s)\\=\pi (r_{1}^{2}+r_{2}^{2}+(r_{1}+r_{2}){\sqrt {(r_{1}-r_{2})^{2}+t^{2}}})\end{aligned}}$

di mana r1 dan r2 adalah jari-jari dasar dan atas, dan s adalah ketinggian miring dari frustum.

Luas permukaan dari frustum hak yang basis reguler mirip n- sisi poligon [luas permukaan polihedron sisi-n] adalah

$L={\frac {n}{4}}\left[(a_{1}^{2}+a_{2}^{2})\cot {\frac {\pi }{n}}+{\sqrt {(a_{1}^{2}-a_{2}^{2})^{2}\sec ^{2}{\frac {\pi }{n}}+4t^{2}(a_{1}+a_{2})^{2}}}\right]$

Lihat pula

• Frustum bola
• Frustum limas
• Frustum polihedron