Kriptografi

Alat kriptografi Lorenz yang dipakai di Jerman saat perang dunia II

Kriptografi (atau kriptologi; dari bahasa Yunani κρυπτός kryptós, "tersembunyi, rahasia"; dan γράφειν graphein, "menulis", atau -λογία logi, "ilmu") merupakan keahlian dan ilmu dari cara-cara untuk komunikasi aman pada kehadirannya di pihak ketiga. Secara umum, kriptografi ialah mengenai mengkonstruksi dan menganalisis protokol komunikasi yang dapat memblokir lawan; berbagai aspek dalam keamanan informasi seperti data rahasia, integritas data, autentikasi, dan non-repudansi merupakan pusat dari kriptografi modern. Kriptografi modern terjadi karena terdapat titik temu antara disiplin ilmu matematika, ilmu komputer, dan teknik elektro. Aplikasi dari kriptografi termasuk ATM, password komputer, dan E-commerce.

Kriptografi sebelum pada termodernisasi merupakan sinonim dari enkripisi, konversi dari kalimat-kalimat yang dapat dibaca menjadi kelihatan tidak masuk akal. Pembuat dari pesan enkripsi membagi teknik pemecahan sandi yang dibutuhkan untuk mengembalikan informasi asli jika hanya dengan penerima yang diinginkan, sehingga dapat mencegah orang yang tidak diinginkan melakukan hal yang sama. Sejak Perang Dunia I dan kedatangan komputer, metode yang digunakan untuk mengelola kriptologi telah meningkat secara komplek dan pengaplikasiannya telah tersebar luar.

Kriptografi modern sangat didasari pada teori matematis dan aplikasi komputer; algoritma kriptografi didesain pada asumsi ketahanan komputasional, membuat algoritma ini sangat sulit dipecahkan oleh musuh. Secara teoritis, sangat sulit memecahkan sistem kriptografi, namun tidak layak melakukannya dengan cara-cara praktis. Skema ini oleh karena itu disebut sangat aman secara komputasional; kemajuan teoritis dapat meningkatkan algoritma faktorisasi integer, dan meningkatkan teknologi komputasi yang membutuhkan solusi ini untuk diadaptasi terus-meneus. Terdapat skema keamanan informasi yang benar-benar tidak boleh dapat ditembuh bahkan dengan komputasi yang tak terbatas namun skema ini sangat sulit diimplementasikan.

Teknologi yang berhubungan dengan kriptologi memiliki banyak masalah legal. Di Inggris, penambahan Regulasi Penyelidikan Aksi Wewenang membutuhkan kriminal yang tertuduh harus menyerahkan kunci dekripsinya jika diminta oleh penegah hukum. Jika tidak pengguna akan menghadapi hukum pidana. Electronic Frontier Foundation (EFF) terlibat dalam sebuah kasus di Amerika Serikat yang mempertanyakan jika seorang tersangka harus untuk menyerahkan kunci dekripsi mereka kepada pengak hukum merupakan inkonstitusionil. EFF memperdebatkan bahwa regulasi ini merupakan pelanggaran hak untuk tidak dipaksa mencurigai dirinya sendiri, seperti dalam Amandemen Kelima Konsitusi Amerika.

Terminologi

Hingga zaman modern kriptografi mengacu hampir secara ekslusif pada enkripsi, yang merupakan proses mengkonversikan informasi biasa menjadi teks yang tak dapat dipahami (disebut teks sandi). Deskripsi merupakan kebalikan, dengan kata lain, memindahkan teks sandi yang tidak dapat dibaca menjadi teks yang dapat dibaca. sandi atau (cypher) merupakan sepasang algoritma yang menciptakan enkripsi dan membalikan dekripsi. Operasi yang lebih mendalam dari sandi diatur baik oleh algoritma dan pada setiap permintaan dekripsi dengan kunci. Kucin ini bersifat rahasia (yang biasanya diketahui hanya oleh orang yang berkomunikasi), dan biasanya terdiri dengan karakter string singkat, yang dibutuhkan untuk mendekripsi teks sandi. Sebelumnya dinamakan "kriptosistem" yang merupakan daftar teratur dari elemen-elemen teks terbatas, teks sandi terbatas, kunci terbatas, dan algoritma dekripsi dan enkripsi yang berkoresponden pada setiap kunci. Kunci sangat penting baik pada penggunaan secara teoritis maupun sebenarnya, di mana sandi tanpa kunci variabel dapat dengan mudah rusak dengan hanya pengetahuan yang digunakan dari sandi dan dengan kemungkinan tidak berguna (atau malam tidak produktif) untuk banyak tujuan. Secara historis, sandi sering digunakan secara langsung untuk enkripsi atau deskripsi tanpa prosedur tambahan seperti autentikasi atau pengecekan integritas.

Dalam penggunaan bahasa sehari-hari, istilah "sandi" sering digunakan untuk menunjukkan setiap metode enkripsi atau penyembunyian arti. Bagaimanapun, dalam kriptografi, sandi telah memiliki arti yang lebih spesifik. Itu berarti pemindahan unit teks (contoh kata atau frase yang berarti) dengan sebuah kata sandi (sebagai contoh, "wallaby" berarti "menyerang saat fajar"). Sandi tidak lagi digunakan pada kriptografi serius-kecuali sesekali untuk beberapa hal yang menyangkut istilah tertentu-sejak sandi yang dipilih secara tepat lebih praktis dan lebih aman daripada sandi terbaik dan juga dapat diadaptasikan pada komputer.

Kriptanalisis merupakan istilah yang digunakan untuk mempelajari metode untuk memperoleh arti dari informasi enkripsi tanpa mengakses sandi secara normal yang dibutuhkan untuk melakukannya; sebagai contoh ilmu yang mempelajari cara untuk memecahkan algoritma enkripsi atau implementasinya.

Beberapa kegunaan dari istilah kriptografi dan kriptologi selalu berubah di Bahasa Inggris, sedang lainnya menggunakan kriptografi untuk merujuk secara spesifik pada penggunakan dan pengaplikasikan dari teknik kriptografi dan kriptologi untuk merujuk pada ilmu kombinasi dari kriptografi dan kriptanalisis. Bahasa Inggris lebih fleksibel dari istilah umum yang digunakan pada beberapa bahasa lain yang dimana kriptologi (dilakukan oleh kriptolog) selalu digunakan pada arti kedua di atas.

Ilmu karateristik dari bahasa yang memiliki aplikasi pada kriptografi (atau kriptologi) (seperti data frekuensi, kombinasi surat, pola universal, dll.) disebuh kriptolinguistik.

Sejarah kriptografi dan kriptanalisis

Sebelum zaman modern, kriptografi dilihat hanya semata-mata berhubungan dengan pesan rahasia (seperti enkripsi)-konversi pesan dari bentuk dapat dipahami menjadi bentuk yang tak dapat dipahami dan kembali lagi satu dengan yang lain, menjadikannya tak dapat dibaca oleh pencegat atau penyadap tanpa ilmu khusus (di mana sandi dibutuhkan untuk dekripsi pesan itu). Enkripsi digunakan untuk menyakinkan kerahasiaan di komunikasi, termasuk teknik untuk pemeriksaan integritas pesan, autentikasi identitas pengirim/penerima, tanda-tangan digital, bukti interaktif dan komputasi keamanan, serta banyak lagi yang lain.

Kriptografi klasik

scytale Yunani yang direkonstruksi kembali, alat sandi pertama kali

Bentuk awal dari penulisan rahasia membutuhkan lebih sedikit dari implementasi penulisan sejak banyak orang tidak dapat membaca. lawan yang lebih terpelajar, membutuhkan kriptografi yang nyata. Tipe sandi klasik utama ialah sandi transposisi, di mana mengatur aturan huruf pada pesan (contoh 'hello world' menajdi 'ehlol owrdl' pada skema pengubahan sederhana ini), dan sandi subtitusi, di mana secara sistematis mengganti huruf atau grup kata dengan kata lainnya dari grup kata (contoh 'fly at once' menjadi 'gmz bu podf' dengan mengganti setiap huruf dengan yang lain di alfabet Latin. Substitusi sandi pada awalnya disebut sandi Caesar, di mana setiap kata pada teks diganti degan huruf dari jumlah tetap pada posisi di alfabet. Laporan Suetonius menyebutkan Julius Caesar mengunakannya untuk berkomunikasi dengan jendral-jendralnya. Atbash merupakan contoh dari sandi Ibrani pada mulanya. Penggunaan awal kriptografi yang diketahui merupakan teks sandi yang diukir pada batu di Mesir (1900 sebelum Masehi), namun teks sandi ini digunakan hanya sebagai hiburan untuk pengamat terpelajar dari pada cara untuk menyimpan informasi.

Yunani kuno menyebutkan telah mengetahui sandi (contoh sandi transposisi scytale yang diklaim telah digunakan oleh militer Sparta. Steganografi (menyembunyikan kehadiran pesan sehingga pesan tersebut menjadi rahasia) juga pertama kali diperkenalkan pada masa kuno. Contoh awal seperti, dari Herodotus, menyembunyikan pesan - sebuah tato pada kepala budaknya - di bawah rambut yang kembali tumbuh. COntoh yang lebih modern dari steganografi termasuk penggunaan tinta tak tampak, mikrodot, dan tanda air digital untuk menyembunyikan informasi.

Di India, Kamasutra dari Vātsyāyana yang berumur 2000 tahun berbicara dengan dua jenis sandi yang berbeda yang disebut Kautiliyam dan Mulavediya. Di Kautiliyam, substitusi kata sandi berdasarkan relasi fonetik, seperti vokal menjadi konsonan. Di Mulavediya, alfabet sandi terdiri dari kata-kata yang berpasangan dan bertimbal-balik.

Lembar pertama dari buku Al-Kindi yang menjelaskan bagaimana mengenkripsikan pesan

Teks sandi yang dihasilkan dengan sandi klasik (dan beberapa sandi modern) selalu mengungkapkan informasi statistik tentang teks awal, yang sering dapat digunakan untuk memecahkannya. Setelah ditemukannya analisis frekuensi oleh matematikawan Arab dan polymath Al-Kindi (juga dikenal sebagai Alkindus) pada abad ke-9, hampir semua jenis sandi menjadi lebih sulit dipecahkan oleh penyerang yang memiliki informasi tersebut. Seperti sandi klasik yang masih populer hingga saat ini, meskipun lebih banyak dalam bentuk puzzle. Al-Kindi menuliskan buku kriptografi yang berjudul Risalah fi Istikhraj al-Mu'amma (Risalah untuk Mnejermahkan Pesan Kriptografi), yang menjelaskan teknik analisis frekuensi kriptanalisis yang pertama kalinya.

Mesin sandi berbentuk buku pada abad ke-16 milik Perancis, ditangan Henri II dari Perancis

Surat terenkripsi dari Gabriel de Luetz d'Amaron, Duta Besar Perancis untuk Kerajaan Ottoman, setelah 1546, dengan penguraian parsial

Pada dasarnya semua sandi tetap rentan kepada kriptanalisis menggunakan teknik analisis frekuensi hingga pengembangan dari sandi polyalphabetic, yang dijelaskan oleh Leon Battista Alberti sekitar tahun 1467, meskipun terdapat beberapa indikasi bahwa hal ini telah terlebih dahulu diketahui oleh Al-Kindi. Penemuan Alberti menggunakan sandi yang berbeda (seperti subtitusi alfabet) untuk beberapa bagian pesan (mungkin untuk setiap teks surat berturut-turut hingga akhir). Dia juga menemukan apa yang mungkin menjadi alat sandi ototmatis untuk pertama kalinya, roda yang menerapkan pelaksanaan dari penemuannya. Pada sandi Vigenère polyalphabetic, enkripsi menggunakan kata kunci, yang mengatur substitusi surat berdasarkan surat mana dari kata kunci yang digunakan. Pada pertengahan abad ke-19 Charles Babbage menunjukkan bahwa sandi Vigenère sangat rentan terhadap pemeriksaan Kasiski, namun hal ini diterbitkan pertama sekali kira-kira sepuluh tahun kemudian oleh Friedrich Kasiski.

Walaupun analisis frekuensi dapat sangat kuat dan menjadi teknik umum melawan banyak sandi, enskripsi masih sangat efektif dalam penerapannya, sebagaimana banyak kriptanalisis masih khawatir akan penerapannya. Memecahkan pesan tanpa menggunakan analisis frekuensi pada dasarnya membutuhkan pengetahuan sandi dan mungkin kunci yang digunakan, sehingga membuat spionase, penyuapan, pencurian, dll. Hal ini secara tegas mengakui kerahasiaan algoritma sandi pada abad 19 sangat tidak peka dan tidak menerapkan praktek keamanan pesan; faktanya, hal ini lebih lanjut disadari bahwa setiap skema kriptografi yang memadai (termasuk sandi) harus tetap aman walaupun musuh benar-benar paham tentang algoritma sandi itu sendiri. Keamanan kunci yang digunakan harus dapat menjamin keamanan pemegang kunci agar tetap rahasia bahkan ketika diserang sekalipun. Prinsip fundamental ini pertama kali dijelaskan pada tahun 1883 oleh Auguste Kerckhoffs dan secara umum dikenal dengan Prinsip Kerckhoff; secara alternatif dan blak-blakan, hal ini dijelaskan kembali oleh Claude Shannon, penemu teori informasi dan fundamental dari teori kriptografi, seperti pribahasa Shanon - 'musuh mengetahui sistemnya'.

Alat-alat bantu yang berbeda telah banyak digunakan untuk membantu sandi. Salah satu alat paling tua yang dikenali merupakan scytale dari Yunani, tangkai yang digunakan oleh Spartan sebagai alat bantuk untuk memindahkan sandi (lihat gambar di atas). Pada zaman pertengahan, alat bantu lainnya ditemukan seperti jerejak sandi, yang juga dikenal sebagai jenis steganografi. Dengan penemuan polialfabetik, sandi menjadi lebih mutakhir dengan bantuan disk sandi milik Alberti, skema tabula recta Johanner Trithemius, dan silinder multi Thomas Jefferson (tidak banyak diketahui, dan ditemukan kembali oleh Bazeries sekitar tahun 1900. Banyak alat mekanik enkripsi/dekripsi ditemukan pada awal abad ke-20, dan beberapa telah dipatenkan, di antaranya mesin rotor yang dikenal dengan nama mesin Enigma digunakan oleh pemerintah dan militer Jerman dari akhir tahun 1920-an dan selama Perang Dunia II. The ciphers implemented by better quality examples of these machine designs brought about a substantial increase in cryptanalytic difficulty after WWI.

Era komputer

Kriptanalisis dari alat mekanis baru terbukti lebih sulit dan melelahkan. Di Inggris, usaha kriptanalisis di Bletchley Park selama Perang Dunia II memacu perkembangan alat yang lebih efisien untuk membawa tugas yang berulang-ulang. Hal ini berujung pada pengembangan Colossus, komputer digital pertama sekali yang bekerja penuh secara elektronik, yang membantu penyandi untuk mendekripsikan mesin Lorenz SZ40/42 milik tentara Jerman.

Seperti juga pengembangan komputer digital dan elektronik, kriptanalisis juga berkembang menjadi lebih kompleks. Lebih jauh lagi, komputer dapat mengenkripsi setiap jenis data yang mungkin dalam bentuk biner, tidak seperti chiper klasik yang hanya mengenkripsi teks bahasa tertulis; hal ini sangat baru dan signifikan. Penggunaan komputer telah menggantikan kirptografi bahasa, baik untuk desain chiper dan kriptanalisis. Banyak chiper komputer dapat dikategorikan dengan operasi mereka pada urutan biner (kadang dalam grup atau blok), tidak seperti skema mekanikal dan klasik, yang biasa memanipulasikan karakter tradisional (seperti surat dan digit) secara langsung. Bagaimanapun, komputer juga membantu kriptanalisis, yang mengimbangi hingga batas tertentu untuk kompleksitas chiper yang lebih tinggi. Namun, chiper modern yang baik telah mengungguli kriptanalisis; kasus ini biasa menggunakan kualitas chiper yang lebih efisien (seperti membutuhkan sumber daya yang sedikit dan cepat, seperti memori atau kapabilitas CPU), sedang mendekripsikannya membutuhkan udaha dengan urutan yang lebih besar, dan lebih luas dibandingkan chiper yang lebih klasik, membuat kriptanalsis menjadi lebih tidak efisien dan tidak berguna.

Riset akademik kriptografi yang terbuka luas masih relatif baru; dimulai pada pertengahan 1970an. Pada saat ini, personel IBM mendesain algoritma yang menjadi standar enkripsi data Federal; Whitfield Diffie dan Martin Hellman mempublikasikan algoritma perjanjian mereka. dan algoritma RSA yang dipublikasikan oleh kolumnis Amerika Martin Gardner. Sejak saat itu, kriptografi telah sangat luas digunakan dalam dunia komunikasi, jaringan komputer, dan keamanan komputer secara umum. Beberapa teknik kriptografi modern dapat menyimpan kunci rahasianya jika menggunakan masalah matematika rumit, seperti faktorisasi integer atau masalah logaritma diskrit, jadi terdapat hubungan yang mendalam dengan matematika abstrak. Tidak ada bukti pasti bahwa teknik kriptografi aman. Saat terbaik, terdapat bukti bahwa beberapa teknik aman jika beberapa masalah komputasional sulit untuk dipecahkan, atau asumsi tertentu mengenai implementasi atau penggunakan praktikal bertemu.

Semakin mengetahui sejarah kriptografi, algoritma kriptografi dan desainer sistem harus juga bijaksana mempertimbangkan pengembangan masa depan saat bekerja dengan desain mereka. Sebagai contoh, pengembangan kontinu pada computer processing power telah meningkatkan cakupan brute-force attack, jadi ketika menentukan panjang kunci, diharuskan memilih kunci yang sulit. Efek potensial dari komputer kuantum telah dipertimbangkan oleh beberapa sistem desainer kriptografi; implementasi kecil dari mesin ini yang akan segera diumumkan mungkin akan membutuhkan perhatian khusus ketimbang hanya spekulatif.

Pada Dasarnya, pada awal abad ke-20, kriptografi secara singkat berkenaan dengan bahasa dan pola lexicographic. Sejak saat itu tekanannya telah berubah, dan kriptografi saat ini lebih luas menggunakan matematika, termasuk aspek teori informasi, kompleksitas komputasional, statistik, kombinasi, aljabar, teori bilangan, dan matematika diskrit secara umum. Kriptografi juga merupakan cabang teknik, namun tidak biasa sebab hal ini berkaitan dengan pertentangan yang aktif, pintar, dan jahat; teknik jenis lain (seperti teknik kimia dan sipil) hanya membutuhkan gaya natural netral. Terdapat juga riset berkembang yang memeriksa hubungan antara masalah kriptografi dan fisika kuantum.

Kriptografi Moderen

Bidang kriptografi yang lebih modern dapat dibagi dalam beberapa area studi. Beberapa yang paling penting akan dibahas di sini.

Kriptografi kunci-simetris

Kriptografi kunci-simetris, di mana satu kunci di gunakan untuk enkripsi dan dekripsi

Kriptografi kunci-simetris merujuk pada metode enskripsi di mana kedua pengirim dan penerima membagi kunci yang sama (atau, walaupun kuncinya tidak mirip, namun dapat berhubungan dengan cara komputasi sederhana). Hal ini menjadi satu-satunya jenis enkripsi yang ketahui publik hingga Juni 1976.[[Image:International Data Encryption Algorithm InfoBox Diagram.svg|thumbnail|Satu putaran (dari 8.5) chiper International Data Encryption Algorithm, digunakan pada beberapa versi PGP (Pretty Good Privacy) untuk enkripsi tingkat tinggi, seperti e-mail Chiper kunci simetris diimplementasikan baik itu sebagai chiper blok atau chiper stream. Sebuah block chiper enchiper masukan pada blok plainteks sebagai lawanan untuk karakter individual, bentuk masukan yang digunakan oleh chiper aliran.

Standar Enkripsi Data (SED) dan Standar Enkripsi Lanjutan (SEL) merupakan desain chiper blok yang telah ditunjuk sebagai standar kriptografi oleh pemerintah Amerika (walaupun penunjukan SED pada akhirnya ditarik setelah SEL diadopsi). Walaupun penarikannya sebagai standar resmi, SED (masih menjadi varian yang masih terbukti dan lebih aman) masih cukup terkenal; Hal ini digunakan oleh banyak penerapan dari enskripsi ATM hingga keamanan e-mail dan akses remote aman. Banyak chiper blok lainnya telah didesain dan dirilis, dengan kualitas yang bervariasi. Banyak telah juga yang dihancurkan, seperti FEAL

Beberapa chiper, yang berbeda dengan tipe 'blok', membuat berkas panjang material kunci yang panjang, di mana dikombinasikan dengan bit-bit teks atau karakter-karakter, sedikit mirip dengan one-time pad. Pada chiper aliran, aliran keluarannya diciptakan berdasarkan keadaan internal yang tersembunyi yang berubah saat chiper bekerja. Keadaan internal mulanya diatur menggunakan bahan kunci rahasia. RC4 sangat luas digunakan sebagai chiper aliran. Chiper blok dapat digunakan sebagai chiper aliran.

Fungsi hash Kriptografi merupakan algoritma kriptografi tipe ke-tiga. Fungsi ini mengambil segala panjang pesan sebagai input, dan panjang keluaran hash yang pendek dan tetap, yang dapat digunakan sebagai (sebagai contoh) tanda tangan digital. Untuk memiliki fungsi hash yang baik, penyerang tidak dapat mencari dua pesan yang dapat menghasilkan hash yang sama. MD4 merupakan fungsi hash pangjang yang sekarang telah dapat dipecahkan; MD5, varian yang lebih kuat dari MD4, sudah luas digunakan namun dapat dipecahkan saat beroperasi. Agensi keamanan nasional Amerika mengembangkan serial Algoritma Hash Aman seperti fungsi hash MD5: SHA-0 ialah algoritma cacat yang kemudian ditarik; SHA-1 digunakan secara luas dan lebih aman dari MD5, namun kriptanalisis telah menemukan serangan padanya; keluarga SHA-2 meningkatkan performa SHA-1, namun belum secara luas digunakan; dan kewenangan Amerika mengatakan hal ini cukup bijaksana dari sudut pandang keamanan untuk mengembangkan standar baru "toolkit algoritma hash NIST secara keseluruhan untuk peningkatan kekuatan secara signifikan. Sehingga, pada tahun 2012, standar nasional Amerika memilih SHA-3 sebagai standar desain hash yang baru.

Message authentication code (MAC) hampir mirip dengan fungsi hash kriptografi, kecuali terdapat kunci rahasia yang dapat digunakan untuk membuktikan nilai hash melalui serangkaian resep; kerumitan tambahan yang melindungi skema serangan algoritma penyingkat sederhana, dan dianggap cukup menguntungkan.

Kriptografi kunci-publik

Kriptogfari kunci-publik, di mana kunci-kunci yang berbeda digunakan untuk enkripsi dan dekripsi

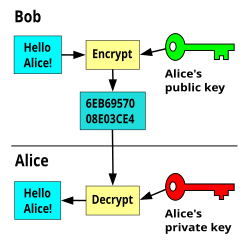
Kriptosistem kunci-simetris menggunakan kunci yang sama untuk enkripsi dan dekripsi sebuah pesan, walaupun pesan atau kelompok pesan dapat memiliki kunci yang berbeda dari yang lain. Kerugian yang paling signifikan dari chiper simetris ialah kebutuhan manajerial kunci untuk menggunakannya secara aman. Setiap sepasang pihak komunikasi yang berbeda harus, idealnya, membagi kunci yang berbeda, dan juga membagi textchiper yang berbeda juga. jumpah kunci yang dibutuhkan meningkat dua kali lipat dari jumlah anggota jaringan, yang sangat cepat membutuhkan skema manajemen kunci komplek untuk menjaga semuanya tetap konsisten dan rahasia. Kesulitan dari menciptakan kunci rahasia yang aman di antara dua pihak yang saling berkomunikasi, ialah, ketika belum adanya jaringan aman di antara keduanya, juga kehadiran chicken-and-egg problem yang dianggap menjadi tantangan praktikal untuk pengguna kriptografi di dunia nyata.

[[Image:Diffie and Hellman.jpg|thumb|left|Whitfield Diffie dan Martin Hellman, penulis jurnal pertama kriptografi kunci-publik]] Pada jurnal pionir tahun 1976, Whifiled Diffie dan Martin Hellman mengusulkan istilah dari kriptografikunci-publik (juga, secara umum, disebut kunci asimetris) pada dua istilah yang berbeda namun secara matematis terdapat kunci yang berhubungan, yaitu kunci publik dan kunci privat. Sistem kunci pablik dikonstruksikan sangat baik sehingga kalkulasi dari satu kunci ('kunci privat') secara komputasional tidak mirip dengan (kunci 'publik') walaupun secara kebutuhan mereka mirip. Malah, kedua kunci dihasilkan secara rahasia, sebagai pasangan yang tidak berhubungan. Sejarawan David Kahn menjelaskan kriptografi kunci-publik sebagai "konsep baru paling revolusioner dalam bidang ini sejak substitusi polialfabetik yang ditemukan pada masa Renaissance

Dalam ekosistem kunci-publik, kunci publik dapat secara bebas terdistribusi, saat pasangannya kunci privat harus selalu terjaga rahasia. Pada sistem enkripsi kunci-publik, kunci publik digunakan untuk enkripsi, sedang kunci privat atau rahasia digunakan untuk dekripsi. Sementara Diffie dan Hellman tidak dapat menemukan sistem seperti itu, mereka menunjukkan bahwa kriptografi kunci-publik memang benar mungkin dengan menunjukkan protokol Diffie-Hellman key exchange, sebuah solusi yang sekarang digunakan secara luas dalam komunikasi aman, mengizinkan dua kelompok untuk secara rahasia membagi kunci enkripsi.

Jurnal Diffie dan Hellman menyebar luas pada dunia akademi dalam mencari sistem enkripsi kunci-publik praktis. Lalu pada tahun 1978 Ronald Rivest, Adi Shamir, dan Len Adleman, menemukan solusi yang kini dikenal sebagai algoritma RSA.

Algoritma Diffie-Hellman dan RSA, sebagai tambahan dalam menciptakan contoh algoritma kunci-publik kualitas tinggi pertama yang dikenal publik, telah sangat luas digunakan. Yang lain termasuk Kriptosistem Cramer-Shoup, Enkripsi ElGamal, dan varian Teknik kurva eliptis.

Lalu, dokumen yang dipublikasikan pada tahun 1997 oleh Government Communication Headquarters (GCHQ), organisasi rahasia Inggris, mengungkapkan bahwa kriptografer di GCHQ telah mengantisipasi beberapa pengembangan akademik. Dilaporkan, sekitar tahun 1970, James H. Ellis telah memahami prinsip kriptografi kunci asimetris. Pada tahun 1973, Clifford Cocks menemukan sulisi yang esensialnya menyerupai algoritma RSA. Dan pada tahun 1974, Malcom J. Williamson diklaim telah mengembangkan algoritma pertukaran Diffie-Hellman.

icon kunci dari browser web Firefox, yang mengindikasikan TLS, sistem kriptografi kunci-publik, sedang digunakan

Kriptografi kunci-publik dapat juga digunakan untuk mengimplementasikan skema tanda tangan digital. Tanda tangan digital berhubungan dengan tanda tangan pada umumnya; mereka memiliki karateristik yang sama dimana mudah bagi pengguna untuk membuatnya, namun sangat sulit bagi orang lain untuk memalsukannya. Tanda tangan digital dapat juga secara permanen mengikat pada konten pesan yang sedang ditanda tangani; mereka lalu tidak dapat 'dipindahkan' dari satu dokumen ke dokumen yang lain, dan setiap usaha akan dapat terdeteksi. Pada skema tanda tangan digital, terdapat dua algoritma: satu untuk menandatangani, di mana kunci rahasia digunakan untuk memproses pesan (atau hash dari pesan, atau keduanya), dan satu untuk verivikasi, di mana kunci publik yang sesuai digunakan dengan pesan untuk memeriksa validitas tanda tangan. RSA dan DSA merupakan dua skema tanda tangan digital yang paling terkenal. Tanda tangan digital merupakan pusat dari operasi infrastruktur kunci publik dan banyak skema keamanan jaringan lainnya (seperti Transport Layer Security, VPN, dll).

Algoritma kunci publik paling sering didasari pada teori masalah kompleksitas komputasional, sering dengan teori bilangan. Sebagai contoh, kekuatan RSA berhubungan dengan masalah faktorisasi integer, sedangkan Diffie-Hellman dan DSA berhubungan dengan masalah logaritma diskrit. Baru-baru saja, kriptografi kurva eliptis telah ditemukan, sistem di mana keamanan yang didasari pada masalah teoritis bilangan yang melibatkan kurva eliptis. Dikarenakan kesulitan masalah pokok, kebanyakan algoritma kunci-publik melibatkan operasi seperti eksponensial dan perkalian aritmatika modular, di mana teknik ini secara komputasional lebih mahal ketimbang teknik yang digunakan pada banyak chiper blok, khususnya dengan ukuran kunci yang dibutuhkan. Hasilnya, kriptosistem kunci-publik seringnya merupakan kriptosistem hybrid, yang merupakan algoritma enkripsi kunci-simetris berkualitas tinggi digunakan untuk pesan itu sendiri, sedang kunci simetris yang relevan dikirimkan dengan pesan, namun dienkripsikan menggunakan algoritma kunci publik. Hampir sama, skema tanda tangan hybrid sering digunakan, di mana fungsi hash kriptogfari dihitung secara komputer, dan hanya hash hasil yang ditanda tangani secara digital.

Kriptanalisis

Varian dari mesin Enigma, digunakan oleh militer dan otoritas Jerman pada akhir tahun 1920an saat Perang Dunia II, mengimplementasikan jenis chiper polialfabetik elektro-mekanikal yang rumit. Membaca dan memecahkan chiper Enigma di Biro chiper Polandia, selama 7 tahun sebelum perang, dan dekripsi di Bletchley Park, menjadi faktor penting kemenangan sekutu.

Tujuan dari kriptanalisis ialah untuk menemukan kelemahan dan ketidakamanan skema kriptografi, sehingga memungkinkan peningkatan atau perbaikan.

Terdapat kesalahpahaman umum bahwa setiap metode enkripsi dapat dipecahkan. Hubungan dengan karya Claude Shannon di Bell Labs pada Perang Dunia II, membuktikan bahwa chiper one-time pad tidak dapat dipecahkan, menemukan kunci utama yang acak, tidak pernah dapat digunakan lagi, menyimpan rahasia dari setiap penyerang, dan memiliki panjang yang sama dan lebih besar dari pesan itu sendiri. Kebanyakan chiper, selain one-time pad, dapat dipecahkan dengan cara komputasional brute force attack, namun jumlah usaha yang dibutuhkan dapat sangat lama tergantung pada besar kunci, sebanding dengan usaha yang dibutuhkan untuk membuat chiper. Pada beberapa kasus, keamanan yang efektif dapat dicapai jika terbuktik bahwa usaha yang dibutuhkan (seperti "faktor kerja", dalam istilah Shannon) melebihi kemampuan dari setiap musuh. Ini berarti bahwa tidak boleh ada metode yang efisien (berbanding terbalik dengan metode brute force yang menghabiskan waktu) dapat ditemukan untuk memecahkan chiper. Sejak tidak ada bukti yang ditemukan, metode one-time-pad tetap secara teoritis merupakan chiper yang tidak dapat dipecahkan.

Terdapat banyak jenis variasi serangan kriptanalitis, dan dapat diklasifikasikan dalam beberapa cara yang berbeda. Perbedaan yang sama yang diketahui oleh penyerang dan kemampuan yang tersedia. Pada serangan chiperteks saja, kriptanalis memiliki akses hanya pada chiperteks (kriptosistem modern yang baik biasanya secara efektif kebal terhadap serangan cipherteks). Pada serangan teks yang diketahui, kriptanalis memiliki akses pada chiperteks dan teks yang berhubungan (atau pada banyak pasangan). Pada serangan teks yang terpilih, kriptanalis memilih teks dan mempelajari tekschiper yang berhubungan (mungkin beberapa kali); sebagai contoh, istilah gardeing yang digunakan oleh Inggris selama Perang dunia II. Akhirnya, pada serangan chiperteks yang terpilih, kriptanalis dapat memilih chiperteks dan belajar teks yang berhubungan. Penting untuk diketahui, walaupun dengan jumlah yang sangat besar, ialah sering terjadinya kesalahan (umumnya pada desain atau penggunaan protokol kriptografis.

Monumen Polandia (tengah) kepada kriptologisnya yang memecahkan mesin cipher Enigma Jerman, dimulai pada tahun 1932, dan berakhir pada Perang Dunia II

Kriptanalisis cipher kunci-simetris biasanya melibatkan mencari serangan melawan cipher blok atau cipher aliran yang lebih efisien dari pada setiap serangan yang dapat melawan cipher sempurna. Sebagai contoh, serangan brute force sederhana melawan DES membutuhkan satu teks yang diketahui dan dekripsi 2⁵⁵, membutuhkan kira-kira setengah dari kunci yang mungkin, untuk mencapai titik kemungkinan mengetahui kunci dapat ditemukan atau tidak. Namun hal ini tidak cukup menjadi jaminan; serangan kriptanalis linear terhadap DES membutuhkan 2⁴³ teks yang deiketahui dan kira-kira 2⁴³ operasi DES. Hal ini dianggap sebagai pengembangan dari serangan brute force.

Algoritma kunci-publik didasari pada kesulitan komputasional pada masalah yang beragam. Kesulitan yang paling terkenal ialah faktorisasi integer (seperti algoritma RSA yang didasari pada masalah yang berhubungan dengan faktor integer), namun masalah logaritma diskrit juga penting. Banyak kriptanalisis kunci-publik berhubungan dengan algoritma numerikal untuk menyelesaikan masalah komputasional ini, dan beberapa darinya, efisien (contoh dalam waktu pengerjaan). Sebagai contoh, algoritma yang paling dikenal untuk menyelesaikan kriptografi kurva eliptik versi logaritma diskrit sangat menghabiskan banyak waktu ketimbang algoritma yang paling dikenal untuk faktorisasi, paling tidak untuk masalah dengan besar yang lebih kurang sama. Oleh karena itu, segala hal harus sama, untuk mencapai kekuatan menahan serangan yang sama, teknik enkripsi berbasis faktor harus menggunakan kunci yang lebih besar dari teknik kurva eliptik. Untuk alasan ini, kriptosistem kunci-publik yang didasari pada kurva eliptik telah menjadi lebih dikenal sejak penemuannya pada pertengahan tahun 1990an.

Sementara kriptanalisis menggunakan kelemahan pada algoritma itu sendiri, serangan pada kriptosistem lainnya didasari pada penggunaan dari algoritma pada perangkat yang nyata, yang disebut side-channel attack. Jika kriptanalis memiliki akses pada, sebagai contoh, jumlah waktu yang dibutuhkan perangkat untuk mengenkripsi jumlah teks atau memberikan laporan kesalahan pada password atau karakter pin, dia mungkin dapat menggunakan serangan waktu untuk memecahkan cipher yang paling tidak tahan pada analisis. Penyerang mungkin juga mempelajari pola dan panjang pesan untuk mendapatkan informasi berharga; hal ini dikenal sebagai analisis trafik dan cukup berguna untuk peringatan serangan. Administrasi kriptosistem yang lemah, seperti mengizinkan kunci yang terlalu pendek, akan membuat setiap sistem menjadi mudah diserang, terlepas dari faktor lainnya. Dan, tentu saja, teknik sosial, dan serangan lain melawan personel yang bekerja dengan kriptosistem atau pesan yang mereka pegang (seperti perampokan, pemerasan, blackmail, espionase, penyiksaan, dll) menjadi serangan yang paling produktif dari semuanya jenis serangan.

Kriptogfari sederhana

Banyak karya teoritikal kriptografi berkaitan dengan kriptografi sederhana-algoritma dengan sifat kriptografi dasar-dan hubungannya pada masalah kriptografi lainnya. Alat kriptografi yang lebih sulit lalu diciptakan dari kriptografi sederhana ini. Kesederhanaan ini menyediakan sifat yang penting, yang digunakan untuk mengembangkan alat yang lebih kompleks yang disebut kriptosistem atau protokol kriptografi, yang menjamin sifat keamanan level satu atau lebih tinggi. Bagaimanapun, perbedaan antara kriptografi sederhana dan kriptosistem, cukup tipis; sebagai contoh, algoritma RSA kadang disebut kriptosistem, dan kadang sederhana. Contoh tipikal kriptografi sederhana termasuk fungsi pseudorandom, fungsi satu-arah, dll.

Kriptosistem

Satu atau lebih kriptografi sederhana sering digunakan untuk mengembangkan algoritma yang lebih kompleks, disebut sistem kriptografi, atau kriptosistem. Kriptosistem (seperti enkripsi ElGamal didesan untuk menyediakan fungsi tertentu (seperti enkripsi kunci publik) sembari menjamin sifat keamanan tertentu keamanan (seperti serangan teks-terpilih) seperti pada model oracle acak. Kriptosistem menggunakan sifat kriptografi sederhana utama untuk mendukung sifat keamanan sistem. Tentu saja, karena perbedaan antara kriptosistem dan kriptografi tidak jelas, kriptosistem yang canggih dapat diperoleh dari kombinasi beberapa kriptosistem sederhana. Pada banyak kasus, struktur kriptosistem melibatkan komunikasi maju mundur di antara dua atau lebih kelompok dalam ruangan. (seperti di antara pengirim dari pesan aman dan penerimanya) atau melewati waktu (seperti data yang dilindungi dengan kriptografi). Kriptosistem yang seperti itu disebut protokol kriptografi.

Beberapa kriptosistem yang terkenal termasuk enkripsi RSA, tanda tangan Schnorr, enkripsi El-Gamal, PGP, dll. Kriptosistem yang lebih rumit melibatkan sistem uang elektronik, sistem tanda-tangan enkripsi, dll. Beberapa kriptosistem teoritikal termasuk sistem pembuktian interaktif, seperti pembuktian pengetahuan-nol), sistem untuk pembagian rahasia,, dll.

Hingga saat ini, banyak sifat keamanan kriptosistem didemonstrasikan menggunakan teknik empirial atau menggunakan alasan ad hoc. Saat ini, terdapat upaya untuk mengembangkan teknik formal untuk menyelesaikan keamanan kriptosistem; Hal ini secara umum disebut keamanan terbukti. Ide umum dari keamanan terbukti ialah untuk memberikan argumen tentang kesulitan komputasional yang dibutuhkan untuk membahayakan aspek keamanan kriptosistem (dari setiap musuh).

Ilmu yang melihat seberapa baik implementasi dan integrasi kriptografi dalam penerapannya pada perangkat lunak disebut bidang tenik kriptografi dan teknik keamanan.

Larangan

Kriptografi telah lama menjadi perhatian untuk mengumpulkan intelejen dan lembaga penegak hukum. Komunikasi rahasia dapat menjadi kriminal atau bahkan penghianatan. Karena fasilitasinya privasi, dan menurunkan sistem privasinya, kriptografi juga dianggap menarik untuk pendukung hak sipil. Oleh karena itu, terdapat sejarah dari masalah legal yang kontroversial mengenai kriptografi, khususnya sejak kehadiran komputer murah yang memungkinkan akses kriptografi kualitas tinggi.

Pada beberapa negara, bahkan penggunaan kriptografi secara domestik ialah, atau telah, dilarang. Hingga tahun 1999, Perancis telah menlarang penggunaan kriptografi secara domestik, walaupun banyak aturan yang kini telah dilonggarkan. Di Cina, dan Iran, lisensi masih dibutuhkan untuk menggunakan kriptografi. Banyak negara telah melarang ketat penggunaan kriptografi. Di antaranya Belarusia, Kazasthan, Mongolia, Pakistan, Singapura, Tunisia, dan Vietman.

Di Amerika, kriptografi legal digunakan pada kalangan domestik, namun terdapat banyak konflik mengenai masalah legal atau tidaknya kegunaan kriptografi. Satu masalah khas yang penting mengani ekspor kriptografi dan kriptografi perangkat lunak dan perangkat keras. Mungkin karena pentingnya kriptanalisis di Perang Dunia II dan ekspektasi bahwa kriptografi akan terus menjadi penting untuk keamanan nasional, banyak pemerintah Barat memiliki, pada satu titik, mengatur kriptografi secara ketat. Setelah Perang Dunia II, ialah ilegal di Amerika untuk menjual atau mendistribusikan teknologi enkripsi ke luar negeri; faktanya, enkripsi ditunjuk sebagai alat militer tambahan dan didaftarkan pada Daftar Perlengkapan Militer Amerika Serikat. Hingga pengembangan komputer personal, algoritma kunci asimetris (seperti teknik kunci publik), dan Internet, bukan terlalu menjadi masalah. Bagaimanapun, semakin Internet dan komputer menjadi tersedia dengan luas, semakin teknik enkripsi kualitas tinggi dikenal luas di seluruh dunia.

Pembatasan ekspor

Pada tahun 1990an, terdapat beberapa tantangan pada regulasi ekpor kriptografi. Setelah kode sumber program Pretty Good Privacy (PGP) milik Philip Zimmermann ditemukan dan digunakan Internet pada Juni 1991, terdapat komplain oleh RSA Security (yang kini dinamakan RSA Data Security, Inc.) menyebabkan investigasi kriminal yang panjang US Costum Service dan FBI, walaupun tidak ada tuntutan yang diberikan kepada Zimmermann. Daniel J. Bernstein, mahasiswa lulusan UC Berkeley, menuntut pemerintah Amerika mengenai beberapa aspek larangan berdasarkan undang-undang dasar negara Amerika. Pada tahun 1995 kasus Bernstein vs Amerika berakhir dengan keputusan pada tahun 1999 mengenai kode sumber cetak untuk algoritma dan sistem kriptografi dilindungi sebagai kebebasan berbicara (atau free speech) oleh Konstitusi Amerika Serikat.

Pada tahun 1996, tiga puluh sembilan negara menandatangani Perjanjian Wassenaar, perjanjian pengawasan senjata yang mengatur ekspor senjata dan teknologi "kegunaan-ganda" seperti kriptografi. Perjanjian ini menetapkan bahwa penggunaan kriptografi dengan panjang-kunci pendek (56-bit untuk enkripsi simetris, 512-bit untuk RSA) tidak akan diatur ekspornya. Kriptografi yang diekspor dari Amerika menjadi kurang diatur diakibatkan perenggangan aturan pada tahun 2000; Tidak ada banyak larangan lagi pada besar kunci di perangkat lunak yang dijual bebas di Amerika. Sejak perenggangan dari larangan ekspor Amerika ini, dan karena komputer personal terhubung dengan Internet termasuk browser web Amerika seperti Firefox atau Internet Explorer, hampir setiap pengguna Internet di dunia memiliki akses pada kriptografi yang berkualitas via browser mereka (seperti, via Transport Layer Security. Program klien email Mozilla Thunderbird dan Microsoft Outlook dapat mentransmit dan menerima email melalui TLS, dan dapat mengirim dan menerima email terenkripsi dengan S/MIME. Banyak pengguna Internet tidak menyadari bahwa perangkat lunak aplikasi dasar mereka mengandung banyak kriptosistem yang sangat luas. Browser dan program email ini terdapat di mana-mana hingga pemerintah yang tugasnya mengatur penggunaan kriptografi secara umum pada dunia sipil tidak dapat menemukan cari yang praktis untuk mengatur distribusi atau penggunaan kriptografi pada kualitas ini, bahkan hukum yang dibuat saat ini oleh pemerintah hampir mustahil dapat dilaksanakan secara efektif.

Keterlibatan NSA

Masalah lain yang sering diperdebatkan mengenai kriptografi di Amerika Serikat ialah pengaruh National Security Agency pada pengembangan dan aturan cipher. NSA terlibat dengan desain Data Encryption Standard selama pengembangannya di IBM dan dipertimbangkan oleh National Bureau Standard sebagai Biro untuk kriptografi. DES didesain untuk tahan terhadap kriptanalisis diferensial, Teknik kriptanalitik umum dan kuat diketahui oleh NSA dan IBM, yang menjadi diketahui publik hanya ketika hal ini ditemukan kembali pada akhir tahun 1980an. Menurut Steven Levy, IBM menemukan kriptanalisis differensial, namun NSA meminta teknik ini tetap terjaga rahasia. Teknik ini menjadi diketahui publik ketika Biham dan Shamir menemukan kembali dan mengumumkannya beberapa tahun kemudian. Keseluruhan keadaan ini mengilustrasikan kesulitan menentukan sumber daya dan pengetahuan apa saja yang penyerang mungkin miliki.

Contoh lain keterlibatan NSA ialah pada masalah chip Clipper pada tahun 1993, mikrochip enkripsi yang bertujuan menjadi bagian dari inisiatif pengawasan-kriptografi Capstone. Clipper dikritik secara luas oleh kriptografer untuk dua alsan. algoritma cipher (yang dinamakan Skipjack) yang dirahasiakan (dibongkar pada tahun 1998, jauh setelah Clipper pertama kali ditemukan). Cipher yang dirahasiakan menyebabkan keprihatinan bahwa NSA secara sengaja membuat cipher lemah untuk membantu usaha intelejennya. Keseluruhan inisiatif ini juga dikritik karena melanggar Prinsip Kerckhoff, karena skema yang termasuk pada escrow key diatur oleh pemerintah untuk digunakan menegakkan hukum, sebagai contoh metode penyadapan.

Manajemen hak digital

Kriptografi merupakan pusat bagi manajemen hak digital (DRM), sebuah kelompok teknik teknologi mengatur penggunaan hak cipta, yang secara luas diimplementasikan dan disebar atas perintah beberapa hak cipta. Pada tahun 1998, Presiden Amerika Bill Clinton menanda-tangani (DMCA) Digital Millennium Copyright Act, yang mengkriminalisasikan segala produksi, penyebaran, dan penggunaan teknik dan teknologi kriptanalitik tertentu (telah ditemukan atau akan ditemukan); termasuk secara spesifik, segala ha lyang dapat digunakan untuk mengelabui skema teknologi DRM. Hal ini memiliki dampak yang nyata pada komunitas riset kriptografi sejak penjanjian ini dibuat di mana selaga riset kriptanalisis melanggar, atau dapat melanggar, DMCA. Undang-undang yang sama telah diberlakukan pada beberapa negara dan wilayah, termasuk implementasi Hak Cipta Direktif. Larangan yang sama juga tercantum pada perjanjian yang ditanda-tangani oleh anggota Organisasi Hak atas Kekayaan Intelektual Dunia.

Departemen Hukum dan Ham serta FBI Amerika belum menegakkan DMCA seperti yang ditakutkan oleh banyak pihak, namun hukumnya, bagaimanapun juga, tetap menjadi kontroversial. Niels Ferguson, peneliti kriptografi yang sangat dihormati, telah mengatakan bahwa dia tidak akan memberikan beberapa risetnya kepada desain kemananan Intel karena ketakutannya dituntut di bawah hukum DMCA. Baik Alan Cox (pengembang kernel Linux kedua) dan Edward Felten (serta beberapa muridnya di Princeton) telah menghadapi banyak masalah terkait undang-undang ini. Dmitry Sklyarov ditangkap selama kunjungannya ke Amerika dari Rusia, dan dihukum selama lima bulan masa percobaan karena dugaan pelanggaran dengan DMCA atas pekerjaan yang telah Ia lakukan di Rusia, di mana hal itu legal di sana. Pada tahun 2007, kunci kriptografi yang bertanggung jawab atas konten Blu-ray dan HD DVD tersebar luas di Internet. Atas kasus itu, MPAA mengirim banyak sekali peringatan penangkapan berdasarkan DMCA, sehingga serangan balasan dari Internet yang dipicu dari dampak yang dirasakan perihal kebebasan berbicara dan Penggunaan wajar.

Pembukaan paksa kunci enkripsi

Di Inggris, undang-undang Inggris memberikan izin kepada polisi untuk memaksa pelaku mengungkapkan berkas dekripsi atau memberikan password yang melindungi kunci enkripsi. Tidak memberikan kunci merupakan pelanggaran hukum, dan dikenakan hukuman dua hingga lima tahun penjara jika melibatkan keamanan nasional. Penuntutan yang berhasil terlah terjadi di bawah undang-undang ini; pertama, di tahun 2009,, menghasilkan 13 bulan penjara. Hukum pemaksaan yang sejenis juga terdapat di Australia, Finlandia, Perancis, dan India memaksa terdakwa untuk memberikan kunci enkripsi atau password selama investigasi kriminal.

Di Amerika Serikat, kasus kriminal Amerika vs Fricosu menunjukkan jika surat perintah dapat memaksa seseorang untuk mengungkapkan kunci enkripsi atau password. Elektronik Frontier Foundation (EFF) memperdebatkan masalah ini atas pelanggaran perlindungan hak asasi manusia berdasarkan Undang-Undang Dasar. Pada tahun 2002, pengadilan membuat undang-undang, bahwa terdakwa harus membawa perangkat keras yang tak terenkripsi ke persidangan.

Dalam banyak yuridikasi, status legal pemaksaan seperti ini masih belum jelas.

Bacaan lebih lanjut

• Becket, B (1988). Introduction to Cryptology. Blackwell Scientific Publications. ISBN 0-632-01836-4. OCLC 16832704.  Excellent coverage of many classical ciphers and cryptography concepts and of the "modern" DES and RSA systems.
• Cryptography and Mathematics by Bernhard Esslinger, 200 pages, part of the free open-source package CrypTool, PDF download di www.cryptool.org (diarsipkan tanggal 20110722183013). CrypTool is the most widespread e-learning program about cryptography and cryptanalysis, open source.
• In Code: A Mathematical Journey by Sarah Flannery (with David Flannery). Popular account of Sarah's award-winning project on public-key cryptography, co-written with her father.
• James Gannon, Stealing Secrets, Telling Lies: How Spies and Codebreakers Helped Shape the Twentieth Century, Washington, D.C., Brassey's, 2001, ISBN 1-57488-367-4.
• Oded Goldreich, Foundations of Cryptography, in two volumes, Cambridge University Press, 2001 and 2004.
• Introduction to Modern Cryptography by Jonathan Katz and Yehuda Lindell.
• Alvin's Secret Code by Clifford B. Hicks (children's novel that introduces some basic cryptography and cryptanalysis).
• Ibrahim A. Al-Kadi, "The Origins of Cryptology: the Arab Contributions," Cryptologia, vol. 16, no. 2 (April 1992), pp. 97–126.
• Christof Paar, Jan Pelzl, Understanding Cryptography, A Textbook for Students and Practitioners. Springer, 2009. (Slides, online cryptography lectures and other information are available on the companion web site.) Very accessible introduction to practical cryptography for non-mathematicians.
• Introduction to Modern Cryptography by Phillip Rogaway and Mihir Bellare, a mathematical introduction to theoretical cryptography including reduction-based security proofs. PDF download.
• Johann-Christoph Woltag, 'Coded Communications (Encryption)' in Rüdiger Wolfrum (ed) Max Planck Encyclopedia of Public International Law (Oxford University Press 2009). *"Max Planck Encyclopedia of Public International Law". , giving an overview of international law issues regarding cryptography.
• Jonathan Arbib & John Dwyer, Discrete Mathematics for Cryptography, 1st Edition ISBN 978-1-907934-01-8.
• Stallings, William (March 2013). Cryptography and Network Security: Principles and Practice (edisi ke-6th). Prentice Hall. ISBN 978-0133354690. 

Pranala Luar

• Definisi kamus kriptografi di Wikikamus
• Media tentang Cryptography di Wikimedia Commons
• Cryptography di In Our Time di BBC. (listen now)
• Crypto Glossary and Dictionary of Technical Cryptography
• NSA's CryptoKids.
• Overview and Applications of Cryptology by the CrypTool Team; PDF; 3.8 MB—July 2008
• A Course in Cryptography by Raphael Pass & Abhi Shelat - offered at Cornell in the form of lecture notes.
• Cryptocorner.com by Chuck Easttom - A generalized resource on all aspects of cryptology.
• For more on the use of cryptographic elements in fiction, see: Dooley, John F., William and Marilyn Ingersoll Professor of Computer Science, Knox College (23 August 2012). "Cryptology in Fiction". 
• The George Fabyan Collection at the Library of Congress has early editions of works of seventeenth-century English literature, publications relating to cryptography.