Himpunan (matematika): Perbedaan antara revisi

Konten dihapus Konten ditambahkan

Sebaris

Revisi terkini sejak 20 Maret 2024 04.35

Dalam matematika, himpunan (bahasa Inggris: set) dapat dibayangkan sebagai kumpulan benda berbeda yang terdefinisi dengan jelas dan dipandang sebagai satu kesatuan utuh^[1]. Dengan terdefinisi yang jelas itu maka dapat ditentukan dengan tegas apakah suatu objek termasuk anggota suatu himpunan atau bukan.

Konsep himpunan seperti saat sekarang ini pertama kali dikemukakan oleh seorang matematikawan Jerman, Georg Cantor, pada akhir abad ke-19. Cantor mendefinisikan himpunan sebagai "Hasil usaha pengumpulan beberapa benda yang memiliki suatu ciri pembeda tertentu dan dapat-diperbedakan dalam intuisi atau pikiran kita (benda-benda itu disebut 'anggota'), menjadi suatu kesatuan".^[2]^[3]

Himpunan merupakan satu di antara konsep dasar matematika, karena hampir semua aspek matematika dapat dibangun dengan konsep himpunan ini.^[4] Kajian lebih lanjut mengenai himpunan dipelajari dalam teori himpunan.

Himpunan dan anggotanya[sunting | sunting sumber]

Suatu himpunan segibanyak

Himpunan yang sama digambarkan dalam "kotak".

Himpunan yang sama digambarkan sebagai "kumpulan benda dalam kotak".

Himpunan secara sederhana dapat diartikan sebagai kumpulan objek-objek. Pengertian "mengumpulkan" atau "menghimpun" sendiri sudah jelas sebab telah sering dilakukan dalam keseharian. Beberapa organisasi menggunakan kata himpunan pada namanya menunjukkan hal tersebut ^[5]. Pengertian himpunan dapat digambarkan sebagai suatu "karung" atau "kotak" yang berisikan unsur-unsurnya^[6]. Penggambaran ini dinisbatkan pada Richard Dedekind ^[7], dan terlukiskan dengan baik dengan diagram Euler-Venn.

Objek dalam suatu himpunan disebut anggota (disebut juga elemen atau unsur). Anggota suatu himpunan dapat berupa apa saja, baik itu bilangan, titik, fungsi, dan lain sebagainya. Himpunan juga boleh jadi berisi objek-objek nyata, seperti sekawanan itik di sawah, semua buku di perpustakaan, sekalian hari dalam sepekan, seluruh huruf dalam alfabet, dan kelimapuluhdua kartu dalam satu set remi..

Keanggotaan suatu objek dapat dinyatakan dengan notasi $\in$ . Pernyataan dengan notasi $a\in S$ dapat dibaca sebagai " $a$ anggota $S$ "; " $a$ di dalam $S$ " ^[8]; " $a$ termasuk dalam $S$ " ^[9]; atau " $a$ milik himpunan $S$ " ^[10].

Ingkaran pernyataan tersebut ( $a$ bukan anggota $S$ ) dapat ditulis sebagai $a\not \in S$ .^[8]

Nama himpunan lazim ditulis menggunakan huruf besar, misalnya ${\textstyle S}$ , ${\textstyle A}$ atau ${\textstyle C}$ , sementara anggota himpunan ditulis menggunakan huruf kecil ( ${\textstyle a}$ , ${\textstyle c}$ , ${\textstyle z}$ ).

Menyatakan dan menuliskan himpunan[sunting | sunting sumber]

Himpunan dapat dinyatakan dan dituliskan secara baku^[11] dengan dua cara.

Pertama, cara pendaftaran, yaitu dengan menulis semua anggota himpunan dalam kurung kurawal, serta antara anggotanya dipisahkan dengan koma. Cara ini baik digunakan untuk himpunan dengan banyak anggota berhingga, terutama juka banyaknya lumayan sedikit. Contohnya himpunan buah $B=\{{\text{apel}},\,{\text{jeruk}},\,{\text{mangga}},\,{\text{pisang}}\}$ . Tanda koma dapat diganti dengan tanda titik koma apabila perlu untuk menghindari kekeliruan dengan tanda koma bilangan desimal, seperti $K=\{0,2;0,4;0,6\}$ .

Jika terlampau banyak untuk dinyatakan satu-persatu bahkan mungkin tak berhingga, tetapi mengikuti pola tertentu, maka dapat digunakan notasi elipsis (...). Contohnya himpunan huruf dalam alfabet $A=\{a,\,b,\,c,\,...,\,y,\,z\}$ atau himpunan bilangan asli $\mathbb {N} =\{1,\,2,\,3,\,4,\,...\}$ .

Kedua, cara merumuskan, yaitu dengan mendefinisikan sifat-sifat yang harus dipenuhi oleh setiap anggota himpunan tersebut. Untuk cara ini syarat tersebut dapat langsung diperkatakan atau ditulis menggunakan notasi pembentuk himpunan.

O=\{u\,|\,u{\mbox{ adalah bilangan ganjil}}\}

E=\{x\,|\,x\in \mathbb {Z} \land (x{\mbox{ mod }}2=0)\}

P=\{p\,|\,p{\mbox{ adalah orang yang pernah menjabat sebagai Presiden RI}}\}

Kesamaan dua himpunan[sunting | sunting sumber]

Himpunan didefinisikan berdasar objek-objek yang termasuk di dalamnya. Dua himpunan bisa saja sama walau disajikan dengan cara yang berbeda^[12], seperti urutan anggotanya tidak sama atau dua himpunan itu dinyatakan dengan penggambaran yang berbeda. Himpunan $A$ dan $B$ disebut sama, jika keduanya memiliki anggota yang sama^[13], dengan kata lain: setiap anggota $A$ adalah anggota $B$ dan sebaliknya, setiap anggota $B$ adalah anggota $A$ .

A=B\equiv \forall _{x}\;x\in {\displaystyle A}\leftrightarrow x\in B

.

Prinsip kesamaan dua himpunan seperti ini, yakni dengan "membuka seluas-luasnya" kedua himpunan itu sehingga tampak semua anggotanya baru kemudian diperbandingkan, sering dirumuskan sebagai aksioma perluasan^[8]. Dengan prinsip ini kesamaan $\{a,b,c\}=\{b,c,a\}$ dan $\{a,b,c\}=\{a,b,b,c,c,c\}$ dapat diketahui. Perhatikan bahwa urutan tidak berpengaruh dalam himpunan, dan perulangan anggota yang sama hanya dihitung satu kali. Contoh lainnya, kita dapat mengatakan bahwa himpunan tiga bilangan prima pertama sama dengan himpunan akar-akar persamaan $x^{3}-10x^{2}+31x-30=0$ . Apabila seluruh anggota kedua himpunan itu didaftarkan, keduanya sama-sama $\{2,3,5\}$ .

Himpunan bagian[sunting | sunting sumber]

Jika setiap anggota $B$ termasuk dalam $A$ , maka himpunan $B$ dikatakan himpunan bagian dari himpunan $A$ , ditulis sebagai $B\subseteq A$ . Secara formal, definisi ini dapat dirumuskan sebagai berikut:

$B\subseteq {\displaystyle A}\equiv \forall _{x}\,x\in B\rightarrow x\in {\displaystyle A}$ .

Dengan menggunakan definisi himpunan bagian, kesamaan dua himpunan juga dapat dinyatakan sebagai berikut:

A=B\equiv {\displaystyle A}\subseteq B\wedge B\subseteq A

.

Definisi di atas sangat berguna untuk membuktikan bahwa dua himpunan $A$ dan $B$ adalah sama. Pertama, buktikan dahulu $A$ adalah himpunan bagian $B$ , kemudian buktikan bahwa $B$ adalah himpunan bagian $A$ .

Banyak anggota himpunan[sunting | sunting sumber]

Kardinalitas suatu himpunan dapat dimengerti sebagai ukuran banyaknya anggota yang ada dalam himpunan tersebut.

Secara formal, dua himpunan $A$ dan $B$ memiliki kardinalitas yang sama, jika terdapat korespondensi satu-satu yang memetakan $A$ pada $B$ .

Jika suatu himpunan ekivalen dengan himpunan $\mathbb {N}$ , yaitu himpunan semua bilangan asli, maka himpunan tersebut disebut himpunan terbilang.^[14] Kardinalitas dari himpunan tersebut disebut sebagai kardinalitas ${\mathfrak {a}}$ . Jika suatu himpunan memiliki kardinalitas yang kurang dari kardinalitas ${\mathfrak {a}}$ , maka himpunan tersebut adalah himpunan berhingga.

Suatu himpunan disebut terhitung jika himpunan tersebut adalah berhingga atau terbilang.

Himpunan yang tidak terhitung disebut himpunan tak terhitung. Contoh dari himpunan ini adalah himpunan semua bilangan riil. Kardinalitas dari himpunan jenis ini disebut sebagai kardinalitas ${\mathfrak {c}}$ . Pembuktian bahwa bilangan riil tidak denumerabel dapat menggunakan pembuktian diagonal. Himpunan bilangan riil dalam interval (0,1) juga memiliki kardinalitas ${\mathfrak {c}}$ , karena terdapat korespondensi satu-satu dari himpunan tersebut dengan himpunan seluruh bilangan riil, yang salah satunya adalah ${\textstyle y=\tan(\pi x-{\frac {1}{2}}\pi )}$ .

Syarat keanggotaan himpunan[sunting | sunting sumber]

Himpunan dapat didefinisikan dengan merumuskan syarat yang harus dipenuhi seluruh anggotanya. Terkadang syarat ini mengikutkan pula dari himpunan semesta mana anggota himpunan baru itu akan diambil. Dengan notasi pembentuk himpunan, secara umum ditulis sebagai

A=\{x\in S\mid P(x)\}

yang dapat dibaca " ${\textstyle A}$ adalah himpunan semua anggota himpunan $S$ sedemikian rupa sehingga pernyataan $P(x)$ benar berlaku".

Operasi himpunan[sunting | sunting sumber]

Gabungan[sunting | sunting sumber]

Gabungan himpunan $A$ dan $B$ . adalah himpunan yang anggotanya adalah anggota A atau B. Dinotasikan $A\cup B$ .

Contoh:

{1, 2} ∪ {1, 2} = {1, 2}.
{1, 2} ∪ {2, 3} = {1, 2, 3}.
{Budi} ∪ {Dani} = {Budi, Dani}.

Beberapa sifat dasar gabungan:

A ⊆ (A ∪ B).
A ⊆ B jika dan hanya jika A ∪ B = B.

Irisan[sunting | sunting sumber]

Irisan antara himpunan *$A$* dan *$B$* .

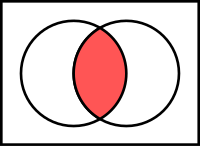
Irisan himpunan $A$ dan $B$ . adalah himpunan yang anggotanya adalah anggota A dan B. Dinotasikan $A\cap B$ .

Jika $A\cap B=\varnothing$ , maka A dan B dapat dikatakan saling pisah.

Contoh:

{1, 2} ∩ {1, 2} = {1, 2}.
{1, 2} ∩ {2, 3} = {2}.
{Budi, Cici} ∩ {Dani, Cici} = {Cici}.
{Budi} ∩ {Dani} = ∅.

Beberapa sifat dasar irisan:

A ∩ B ⊆ A.
A ⊂ B jika dan hanya jika A ∩ B = A.

Komplemen[sunting | sunting sumber]

Pelengkap (komplemen) himpunan $A$ adalah himpunan yang anggotanya bukan anggota $A$ . Dinotasikan $A^{c}$ atau $A'$ .

Contoh:

{1, 2} \ {1, 2} = ∅.
{1, 2, 3, 4} \ {1, 3} = {2, 4}.

Beberapa sifat dasar komplemen:

A \ B ≠ B \ A untuk A ≠ B.
(A′)′ = A.
A \ A = ∅.
A \ B = A ∩ B′.

Konsep komplemen dapat diperluas menjadi beda setangkup (pengurangan himpunan), jika diterapkan untuk himpunan A dan B atau A - B menghasilkan

A\,\Delta \,B=(A\setminus B)\cup (B\setminus A).

Contohnya, diferensi simetris antara:

{7, 8, 9, 10} dan {9, 10, 11, 12} adalah {7, 8, 11, 12}.
{Ana, Budi, Dedi, Felix} dan {Budi, Cici, Dedi, Ela} adalah {Ana, Cici, Ela, Felix}.

Komplemen $B$ terhadap $A$ .
Komplemen $A$ terhadap $U$ .
Beda setangkup himpunan $A$ dan $B$ .

Hasil Kali Kartesian[sunting | sunting sumber]

atau perkalian himpunan merupakan operasi yang menggabungkan anggota suatu himpunan dengan himpunan lainnya. Perkalian himpunan antara A dan B didefinisikan dengan A × B. Anggota himpunan | A × B | adalah pasangan terurut (a,b) dimana a adalah anggota himpunan {\displaystyle A} dan b adalah anggota himpunan B.

Contoh:

{1, 2} × {x, y} = {(1, x), (1, y), (2, x), (2, y)}.
{1, 2} × {a, b, c} = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c) }.
{1, 2} × {1, 2} = {(1, 1), (1, 2), (2, 1), (2, 2)}.

Beberapa sifat dasar himpunan perkalian:

A × ∅ = ∅.
A × (B ∪ C) = (A × B) ∪ (A × C).
(A ∪ B) × C = (A × C) ∪ (B × C).
| A × B | = | B × A | = | A | × | B |.

Himpunan khusus[sunting | sunting sumber]

Himpunan $\mathbb {N}$ termuat dalam $\mathbb {Z}$ , yang termuat dalam $\mathbb {Q}$ , yang termuat dalam $\mathbb {R}$ , yang termuat dalam $\mathbb {C}$ .

Sejumlah himpunan yang begitu penting dan sering terpakai dalam matematika, sehingga mendapat nama dan lambang tersendiri, seperti:

$\mathbb {N}$ , himpunan bilangan asli {1, 2, 3, 4, ...};
$\mathbb {Z}$ , himpunan bilangan bulat {..., -3, -2, -1, 0, 1, 2, 3, ...};
$\mathbb {Q}$ , himpunan bilangan rasional;
$\mathbb {R}$ , himpunan bilangan riil;
$\mathbb {C}$ , himpunan bilangan kompleks;
$\mathbb {H}$ , himpunan bilangan kuarternion.

Himpunan di atas memiliki tak hingga anggota, dan masing-masing merupakah himpunan bagian dari himpunan yang tersenarai di bawahnya.

Himpunan n-rangkap bilangan riil biasa dilambangkan dengan $\mathbb {R} ^{n}$ untuk $n$ sebarang bilangan asli. Sebagai contoh, $\mathbb {R} ^{2}$ adalah himpunan pasangan terurut $(a,b)$ dengan $a,b\in \mathbb {R}$ .

Lihat juga[sunting | sunting sumber]

Kelas (teori himpunan), himpunan dari himpunan-himpunan.
Aljabar himpunan, sifat-sifat operasi himpunan.
Fungsi karakteristik, fungsi yang menunjukkan apakah sesuatu itu anggota himpunan atau bukan.

Referensi[sunting | sunting sumber]

^ Afidah Khairunnisa (2018). Matematika Dasar. Depok: Rajawali Pers. ISBN 978-979-769-764-8.
^ Hakim., Nasoetion, Andi (1982). Landasan matematika. Bhratara Karya Aksara. OCLC 974924773.
^ Prof. Dr. Wahyudin M.Pd. (2019). Hakikat dan Sejarah Matematika. Tanggerang Selatan: Universitas Terbuka.
^ Ferreirós, José (2020). Zalta, Edward N., ed. The Stanford Encyclopedia of Philosophy (edisi ke-Summer 2020). Metaphysics Research Lab, Stanford University.
^ Dumairy (2003). Matematika Terapan Untuk Bisnis dan Ekonomi. Yogyakarta: BPFE.
^ Halmos, Paul Richard (1960). Naive Set Theory (dalam bahasa Inggris). Van Nostrand. ISBN 978-3-540-90092-4.
^ Oliver, Alex; Smiley, Timothy (2006). "What Are Sets and What Are They For?". Philosophical Perspectives. 20: 123–155. ISSN 1520-8583.
^ ^a ^b ^c Lipschutz, Seymour (1995). Teori Himpunan. Diterjemahkan oleh Pantur Silaban. Jakarta: Erlangga.
^ Walpole, Ronald E. (1995). Pengantar Statistika. Diterjemahkan oleh Ir. Bambang Sumantri. Jakarta: Gramedia Pustaka Utama.
^ Dr. Jaka Nugraha (2020). Pengantar Peluang dan Distribusi. Sleman: Deepublish.
^ Marsudi (2010-10-08). Logika dan Teori Himpunan. Universitas Brawijaya Press. ISBN 978-979-8074-51-6.
^ Rinaldi Munir (2010). Matematika Diskrit. Bandung: Informatika Bandung.
^ Julan Hernadi (2021). Fondasi Matematika & Metode Pembuktian. Ponorogo: UMPO Press.
^ Hendra Gunawan (2017). Menuju Tak Terhingga. Bandung: ITB Press.

Bacaan lanjutan[sunting | sunting sumber]

Dauben, Joseph W., Georg Cantor: His Mathematics and Philosophy of the Infinite, Boston: Harvard University Press (1979) ISBN 978-0-691-02447-9.
Halmos, Paul R., Naive Set Theory, Princeton, N.J.: Van Nostrand (1960) ISBN 0-387-90092-6
Stoll, Robert R., Set Theory and Logic, Mineola, N.Y.: Dover Publications (1979) ISBN 0-486-63829-4
Velleman, Daniel, How To Prove It: A Structured Approach, Cambridge University Press (2006) ISBN 978-0-521-67599-4

Pranala luar[sunting | sunting sumber]

[1] Afidah Khairunnisa (2018). Matematika Dasar. Depok: Rajawali Pers. ISBN 978-979-769-764-8.

[:2-2] Hakim., Nasoetion, Andi (1982). Landasan matematika. Bhratara Karya Aksara. OCLC 974924773.

[3] Prof. Dr. Wahyudin M.Pd. (2019). Hakikat dan Sejarah Matematika. Tanggerang Selatan: Universitas Terbuka.

[4] Ferreirós, José (2020). Zalta, Edward N., ed. The Stanford Encyclopedia of Philosophy (edisi ke-Summer 2020). Metaphysics Research Lab, Stanford University.

[5] Dumairy (2003). Matematika Terapan Untuk Bisnis dan Ekonomi. Yogyakarta: BPFE.

[6] Halmos, Paul Richard (1960). Naive Set Theory (dalam bahasa Inggris). Van Nostrand. ISBN 978-3-540-90092-4.

[7] Oliver, Alex; Smiley, Timothy (2006). "What Are Sets and What Are They For?". Philosophical Perspectives. 20: 123–155. ISSN 1520-8583.

[:0-8] Lipschutz, Seymour (1995). Teori Himpunan. Diterjemahkan oleh Pantur Silaban. Jakarta: Erlangga.

[9] Walpole, Ronald E. (1995). Pengantar Statistika. Diterjemahkan oleh Ir. Bambang Sumantri. Jakarta: Gramedia Pustaka Utama.

[10] Dr. Jaka Nugraha (2020). Pengantar Peluang dan Distribusi. Sleman: Deepublish.

[:3-11] Marsudi (2010-10-08). Logika dan Teori Himpunan. Universitas Brawijaya Press. ISBN 978-979-8074-51-6.

[:1-12] Rinaldi Munir (2010). Matematika Diskrit. Bandung: Informatika Bandung.

[13] Julan Hernadi (2021). Fondasi Matematika & Metode Pembuktian. Ponorogo: UMPO Press.

[14] Hendra Gunawan (2017). Menuju Tak Terhingga. Bandung: ITB Press.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

l b s Teori himpunan
Umum	Himpunan (matematika)
Aksioma	Adjungsi Batas ukuran Determinasi Gabungan Himpunan kuasa Keberaturan Kebisadibangunan (V=L) Perluasan Pasangan Pemilihan tercacah terikat global Takhingga Aksioma Martin Skema aksioma penggantian spesifikasi
Operasi	Gabungan Gabungan lepas Himpunan kuasa Hukum De Morgan Irisan Komplemen Produk Kartesius Selisih himpunan Beda setangkup
Konsep Metode	Argumen diagonal Bilangan kardinal (besar) Bilangan ordinal Diagram Venn Elemen pasangan terurut rangkap Hipotesis kontinum Induksi lintas-hingga Kardinalitas Kelas Keluarga Korespondensi satu-ke-satu Pemaksaan Semesta yang bisa dibangun
Jenis himpunan	Himpunan bagian · Superhimpunan Berhingga (turun-temurun) Takhingga (takhingga Dedekind) Kabur Kosong Rekursif Semesta Tercacah Tak tercacah Transitif
Teori	Aksiomatik Alternatif Naif Teorema Cantor Zermelo Umum Principia Mathematica New Foundations (NF, NFU) Zermelo–Fraenkel (ZFC) von Neumann–Bernays–Gödel (NBG) Morse–Kelley Kripke–Platek Tarski–Grothendieck
Paradoks Masalah	Paradoks Russell Masalah Suslin Paradoks Burali-Forti
Teoretisi himpunan	Abraham Fraenkel Bertrand Russell Ernst Zermelo Georg Cantor John von Neumann Kurt Gödel Paul Bernays Paul Cohen Richard Dedekind Thomas Jech Thoralf Skolem Willard Quine

l b s Jenis himpunan berdasarkan cabang matematika
Teori himpunan	Himpunan (matematika) Himpunan bagian (Subhimpunan) Himpunan Fin Himpunan hingga Himpunan kabur Himpunan kosong Himpunan pangkat Himpunan rekursif Himpunan saling lepas Himpunan semesta Himpunan takhingga Himpunan taktercacahkan Himpunan tercacahkan Himpunan transitif
Analisis kompleks	Himpunan Julia Himpunan Mandelbrot
Teori tatanan	Himpunan terurut parsial
Topologi	Himpunan cembung Himpunan terbuka