Pengguna:Kekavigi/bak pasir: Perbedaan antara revisi
k ~ |
k ~ Tag: halaman dengan galat skrip VisualEditor |
||
| Baris 1: | Baris 1: | ||
Dalam [[aljabar linear]], '''basis''' adalah himpunan vektor, yang dalam sebuah [[kombinasi linear]] dapat merepresentasikan setiap vektor dalam suatu [[ruang vektor]]. Tidak ada elemen dalam himpunan vektor tersebut yang dapat direpresentasikan sebagai kombinasi linear vektor-vektor lain. Basis juga dapat dianggap sebagai "[[sistem koordinat]]".<ref>Halmos, Paul Richard (1987) ''Finite-dimensional vector spaces'' (4<sup>th</sup> edition) Springer-Verlag, New York, [http://books.google.co.uk/books?id=mdWeEhA17scC&pg=PA10 page 10], ISBN 0-387-90093-4</ref> |
|||
{{Short description|Perubahan koordinat di aljabar linear}} |
|||
[[Berkas:3d basis transformation2.svg|jmpl|[[Ruang vektor]] pada yang dibangun dari [[Basis (aljabar linear)|basis]] berisi vektor-vektor berwarna ungu, dapat dibangun pula dari basis berisi vektor-vektor berwarna merah. Dengan menyusun setiap vektor berwarna ungu menjadi [[kombinasi linear]] vektor-vektor berwarna merah (dan sebaliknya), pernyataan yang disampaikan menggunakan basis ungu juga dapat disampaikan menggunakan basis merah (dan sebaliknya). ]] |
|||
Dalam [[aljabar linear]], [[Basis (aljabar linear)|basis terurut]] memungkinkan setiap elemen pada sebarang [[ruang vektor]] [[dimensi|berdimensi]] <math>n</math> dinyatakan dalam bentuk vektor koordinat, yakni suatu [[barisan]] <math>n</math>-[[Skalar (matematika)|skalar]] yang disebut [koordinat]. Untuk dua basis berbeda dari suatu ruang vektor, vektor koordinat yang menyatakan elemen <math>v</math> atas basis pertama, umumnya berbeda dengan vektor koordinat yang menyatakan elemen yang sama, namun atas basis yang kedua. '''Perubahan basis''' adalah tindakan mengubah penyataan-pernyataan matematika pada suatu basis, ke pernyataan-pernyataan yang sepadan pada basis yang lain.<ref>{{harvtxt|Anton|1987|pp=221–237}}</ref><ref>{{harvtxt|Beauregard|Fraleigh|1973|pp=240–243}}</ref><ref>{{harvtxt|Nering|1970|pp=50–52}}</ref> |
|||
== Definisi formal == |
|||
Perubahan basis tersebut dihasilkan dari ''rumus perubahan-basis'' yang menyatakan koordinat-koordinat relatif pada satu basis dalam bentuk koordinat-koordinat relatif basis yang lainnya. Menggunakan [[Matriks (matematika)|matriks]], rumus ini dapat dituliskan sebagai |
|||
Basis untuk ruang vektor <math>V</math> (atas [[Medan (matematika)|medan]] <math>F</math>) adalah suatu himpunan bagian <math>B\subset V</math> yang memenuhi: |
|||
# Setiap <math>\mathbf{v}\in V</math> dapat dituliskan sebagai <math>\mathbf{v}=\sum _{i=1}^ka_i\mathbf{b}_i</math> dengan <math>k\in\mathbb{N}, a_1,\ldots,a_k\in F, \mathbf{b}_1,\ldots,\mathbf{b}_k\in B</math>. |
|||
:<math>\mathbf x_\mathrm{lama} = \mathbf{A} \,\mathbf x_\mathrm{baru},</math> |
|||
# Jika <math>\mathbf{v}=\sum _{i=1}^{\tilde{k}}\tilde{a}_i\tilde{\mathbf{b}}_i</math> representasi lain, maka <math>k=\tilde{k}</math> dan ada suatu permutasi <math>\iota:\{1,\ldots,k\}\to\{1,\ldots,k\}</math> yang <math>a_i=\tilde{a}_{\iota (i)}</math> dan <math>\mathbf{b}_i=\tilde{\mathbf{b}}_{\iota (i)}</math>. |
|||
dengan "lama" dan "baru" masing-masing merujuk pada basis lama dan basis baru, <math>\mathbf x_\mathrm{lama}</math> dan <math>\mathbf x_\mathrm{baru}</math> adalah vektor kolom dari koordinat vektor yang sama menurut kedua basis, dan <math>\mathbf{A}</math> adalah ''matriks perubahan-basis'' (juga disebut ''matriks transisi'') yang kolom-kolomnya menyatakan koordinat vektor-vektor basis lama di basis baru. |
|||
Artikel ini fokus membahas ruang vektor dimensi hingga. Akan tetapi, banyak prinsip yang disampaikan disini juga berlaku pada ruang vektor dimensi tak-hingga. |
|||
== Contoh == |
== Contoh == |
||
[[Berkas:Basis graph (no label).svg|thumb|400px|Gambar ini mengilustrasikan [[basis standar]] pada '''''R'''<sup>2</sup>''. Vektor biru dan oranye adalah elemen dasarnya; vektor hijau dapat diberikan dalam istilah vektor basis, dan begitu juga [[bergantung linear]] padanya.]] |
|||
Misalkan kita ingin menentukan vektor koordinat pada [[Ruang Euklides|ruang vektor Euklides]] <math>\mathbb R^2,</math> yang dihasilkan dari rotasi sebesar <math>t.</math> Ruang vektor sebelum dirotasi memiliki [[Basis (aljabar linear)|basis standar]] <math>v_1= (1,0)</math> dan <math>v_2= (0,1);</math> sebut ini sebagai basis "lama". Setelah ruang vektor dirotasi, basis tersebut ikut berotasi, dan berubah menjadi <math>w_1=(\cos t, \sin t)</math> dan <math>w_2=(-\sin t, \cos t);</math> sebut ini sebagai basis "baru". Lalu, matriks perubahan basis akibat rotasi dapat dituliskan sebagai<math display="block">\begin{bmatrix} |
|||
*Himpunan [[eksponen atas himpunan |{{math|'''R'''<sup>2</sup>}}]] dari [[pasangan terurut]] dari [[bilangan riil]] adalah ruang vektor untuk penjumlahan berdasarkan komponen |
|||
\cos t& -\sin t\\ |
|||
::<math>(a, b) + (c, d) = (a + c, b+d),</math> |
|||
\sin t& \cos t |
|||
:dan perkalian skalar |
|||
\end{bmatrix}.</math>Rumus perubahan basis menyatakan bahwa, jika <math display="inline">(y_1,\, y_2)</math> adalah koordinat baru hasil rotasi dari vektor koordinat <math>(x_1,\, x_2),</math> maka |
|||
::<math>\lambda (a,b) = (\lambda a, \lambda b),</math> |
|||
: <math>\begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix} |
|||
:dimana <math>\lambda</math> adalah bilangan real apa pun. Basis sederhana dari ruang vektor ini, disebut [[basis standar]] terdiri dari dua vektor {{math|1=''e''<sub>1</sub> = (1,0)}} and {{math|1=''e''<sub>2</sub> = (0,1)}}, karena vektor apapun {{math|1=''v'' = (''a'', ''b'')}} dari {{math|'''R'''<sup>2</sup>}} dapat ditulis secara unik sebagai |
|||
\cos t& -\sin t\\ |
|||
::<math>v= ae_1+be_2.</math> |
|||
\sin t& \cos t |
|||
:Pasangan vektor bebas linear lainnya {{math|'''R'''<sup>2</sup>}}, seperti {{math|(1, 1)}} dan {{math|(−1, 2)}}, bentuk menjadi dasar {{math|'''R'''<sup>2</sup>}}. |
|||
\end{bmatrix}\,\begin{bmatrix}y_1\\y_2\end{bmatrix}.</math> |
|||
*Lebih umum lagi, jika {{mvar|F}} adalah [[medan (matematika)|bidang]], himpunan <math>F^n</math> dari [[tupel|{{mvar|n}}-tupel]] dari elemen {{mvar|F}} adalah ruang vektor untuk penjumlahan dan [[perkalian skalar]] yang didefinisikan serupa. Karena |
|||
::<math>e_i = (0, \ldots, 0,1,0,\ldots, 0)</math> |
|||
:jadilah tupel {{mvar | n}} dengan semua komponen sama dengan 0, kecuali {{mvar|i}} yaitu 1. Kemudian <math>e_1, \ldots, e_n</math> adalah basis dari <math>F^n</math> yang disebut '' basis standar '' dari <math>F^n.</math> |
|||
*Jika {{mvar|F}} adalah bidang [[gelanggang polinomial]] {{math|''F''[''X'']}} dari [[polinomial]] dalam satu [[tak tentu (variabel)|tak tentu]] memiliki basis {{mvar|B}}, yang disebut [[basis monomial]], yang terdiri dari semua [[monomial]]: |
|||
::<math>B=\{1, X, X^2, \ldots\}.</math> |
|||
:Kumpulan polinomial apa pun yang hanya ada satu polinomial pada setiap derajat juga merupakan basis. Kumpulan polinomial seperti itu disebut [[urutan polinomial]]. Contoh (di antara banyak) urutan polinomial tersebut adalah [[polinomial Bernstein|polinomial basis Bernstein]], dan [[polinomial Chebyshev]]. |
|||
== Koordinat {{anchor|Basis dan koordinat order}} == |
|||
Sehingga, |
|||
Misalkan {{mvar|V}} menjadi ruang vektor berdimensi berhingga {{mvar|n}} di atas bidang {{mvar|F}}, dan |
|||
: <math>x_1=y_1\cos t - y_2\sin t \qquad\text{dan}\qquad x_2=y_1\sin t + y_2\cos t. </math> |
|||
:<math>B=\{b_1, \ldots, b_n\}</math> |
|||
menjadi dasar dari {{mvar|V}}. Menurut definisi basis, setiap {{mvar|v}} pada {{mvar|V}} dapat ditulis, dengan cara yang unik, seperti |
|||
:<math>v=\lambda_1 b_1 + \cdots + \lambda_n b_n,</math> |
|||
dimana koefisiennya <math>\lambda_1, \ldots, \lambda_n</math> adalah skalar (yaitu, elemen {{mvar|F}}), yang disebut '' koordinat '' dari {{mvar|v}} di atas {{mvar|B}}. Namun, jika seseorang berbicara tentang '' himpunan '' koefisien, seseorang kehilangan korespondensi antara koefisien dan elemen basis, dan beberapa vektor mungkin memiliki '' himpunan '' koefisien yang sama. Sebagai contoh, <math>3b_1 +2b_2</math> dan <math>2b_1 +3b_2</math> memiliki koefisien yang sama {{math|{2, 3}{{void}}}}, dan berbeda. Oleh karena itu, sering kali nyaman untuk bekerja dengan '''dasar yang teratur'''; ini biasanya dilakukan oleh [[kumpulan indeks|pengindeksan]] elemen dasar oleh bilangan asli pertama. Kemudian, koordinat vektor membentuk [[urutan (matematika)|urutan]] dengan indeks serupa, dan vektor sepenuhnya dicirikan oleh urutan koordinat. Basis terurut juga disebut '''frame''', kata yang biasa digunakan, dalam berbagai konteks, untuk merujuk ke urutan data yang memungkinkan penentuan koordinat. |
|||
Misalkan, seperti biasa, <math>F^n</math> menjadi himpunan [[tupel|{{mvar|n}}-tupel]] dari elemen {{mvar|F}}. Himpunan ini adalah {{mvar|F}} ruang vektor, dengan penjumlahan dan perkalian skalar ditentukan berdasarkan komponen. Peta |
|||
Hubungan tersebut dapat dibuktikan dengan menunjukkan <math>(x_1,\, x_2)</math> dan <math display="inline">(y_1,\, y_2)</math> merujuk pada objek yang sama, |
|||
:<math>\varphi: (\lambda_1, \ldots, \lambda_n) \mapsto \lambda_1 b_1 + \cdots + \lambda_n b_n</math> |
|||
is a [[linear isomorphism]] from the vector space <math>F^n</math> onto {{mvar|V}}. In other words, <math>F^n</math> is the [[coordinate space]] of {{mvar|V}}, and the {{mvar|n}}-tuple <math>\varphi^{-1}(v)</math> is the [[coordinate vector]] of {{mvar|v}}. |
|||
[[Gambar invers]] oleh <math>\varphi</math> pada <math>b_i</math> adalah {{mvar|n}}-tupel <math>e_i</math> semua yang komponennya 0, kecuali yang ke {{mvar|i}} yaitu 1. <math>e_i</math> membentuk dasar terurut dari <math> F ^ n, </math> yang disebut [[standar dasar]] atau [[dasar kanonik]]. Dasar yang diurutkan {{mvar|B}} adalah gambar oleh <math>\varphi </math> dari dasar kanonik <math>F^n</math>. |
|||
: <math>\begin{align} |
|||
x_1v_1+x_2v_2 &= (y_1\cos t - y_2\sin t) v_1 + (y_1\sin t + y_2\cos t) v_2\\ |
|||
&= y_1 (\cos (t) v_1 + \sin(t)v_2) + y_2 (-\sin(t) v_1 +\cos(t) v_2)\\ |
|||
&=y_1w_1+y_2w_2. |
|||
\end{align}</math> |
|||
: |
|||
Ini mengikuti dari apa yang mendahului setiap basis terurut adalah gambar dengan [[isomorfisme]] linier dari basis kanonik <math>F^n</math>, dan bahwa setiap isomorfisme linier dari <math>F^n</math> ke {{mvar|V}} dapat didefinisikan sebagai isomorfisme yang memetakan dasar kanonik <math>F^n</math> ke urutan tertentu dasar dari {{mvar|V}}. Dengan kata lain, ini setara dengan mendefinisikan basis terurut dari {{mvar|V}}, atau isomorfisme linier dari <math>F^n</math> ke {{mvar|V}}. |
|||
== Rumus perubahan basis == |
|||
Misalkan <math>B_\mathrm{lama}=(v_1,\, \ldots,\, v_n)</math> adalah basis dari suatu [[ruang vektor]] dimensi hingga {{mvar|V}} atas suatu [[Lapangan (matematika)|lapangan]] {{mvar|F}}.{{efn|Although a basis is generally defined as a set of vectors (for example, as a spanning set that is linearly independent), the [[tuple]] notation is convenient here, since the indexing by the first positive integers makes the basis an [[ordered basis]].}} Seorang dapat mendefinisikan <math>n</math> vektor baru <math>w_j;</math> (dengan <math>j=1,\,\dots,\, n</math>) berdasarkan koordinat vektor tersebut <math>a_{i,j}</math> atas <math>B_\mathrm{lama}\colon </math> |
|||
== Perubahan basis == |
|||
: <math>w_j=\sum_{i=1}^n a_{i,j}v_i.</math> |
|||
{{main|Perubahan basis}} |
|||
Maka {{math|''V''}} jadilah ruang vektor berdimensi {{mvar|n}} di atas bidang {{math|''F''}}. Diberikan dua pangkalan (order) <math>B_\mathrm {old}=(v_1, \ldots, v_n)</math> dan <math>B_\mathrm {new}=(w_1, \ldots, w_n)</math> dari {{math|''V''}}, sering kali berguna untuk menyatakan koordinat vektor {{mvar | x}} sehubungan dengan <math>B_\mathrm {old}</math> dalam hal koordinat sehubungan dengan <math>B_\mathrm {new}.</math> Ini dapat dilakukan dengan '' rumus perubahan-basis '', yang dijelaskan di bawah ini. Subskrip "lama" dan "baru" telah dipilih karena biasa digunakan untuk merujuk <math>B_\mathrm {old}</math> dan <math>B_\mathrm {new}</math> sebagai '' dasar lama '' dan '' dasar baru ''. Ini berguna untuk menggambarkan koordinat lama dengan yang baru, karena, secara umum, seseorang memiliki [[ekspresi (matematika) | ekspresi]] yang melibatkan koordinat lama, dan jika seseorang ingin mendapatkan ekspresi yang setara dalam hal koordinat baru; ini diperoleh dengan mengganti koordinat lama dengan ekspresi mereka dalam bentuk koordinat baru. |
|||
Biasanya, vektor basis baru diberikan oleh koordinatnya di atas basis lama, yaitu |
|||
Misalkan |
|||
:<math>w_j=\sum_{i=1}^n a_{i,j}v_i.</math> |
|||
If <math>(x_1, \ldots, x_n)</math> and <math>(y_1, \ldots, y_n)</math> are the coordinates of a vector {{mvar|x}} over the old and the new basis respectively, the change-of-basis formula is |
|||
:<math>x_i = \sum_{j=1}^n a_{i,j}y_j,</math> |
|||
for {{math|1=''i'' = 1, ..., ''n''}}. |
|||
Rumus ini dapat ditulis secara ringkas dalam notasi [[matriks (matematika) | matriks]]. Misalkan {{mvar|A}} adalah matriks dari <math>a_{i,j},</math> dan |
|||
: <math>\mathbf{A}=\left(a_{i,j}\right)_{i,j}</math> |
|||
:<math>X= \begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix}\quad</math> dan <math>\quad Y= \begin{pmatrix}y_1\\\vdots\\y_n\end{pmatrix}</math> |
|||
jadilah [[vektor kolom]] dari koordinat {{mvar|v}} di basis lama dan basis baru, maka rumus untuk mengubah koordinat adalah |
|||
:<math>X=AY.</math> |
|||
Rumusnya dapat dibuktikan dengan mempertimbangkan dekomposisi vektor {{mvar|x}} pada dua basa: satu memiliki |
|||
sebagai [[Matriks (matematika)|matriks]] yang kolom ke-{{mvar|j}}-nya dibentuk dari koordinat <math>w_j</math>. (Di bagian ini dan seterusnya, indeks {{mvar|i}} selalu digunakan untuk merujuk baris di <math>\mathbf{A}</math> dan <math>v_i,</math> sedangkan indeks {{mvar|j}} selalu digunakan untuk merujuk kolom di <math>\mathbf{A}</math> dan <math>w_j;</math> konvensi ini berguna untuk menghindari kesalahan dalam perhitungan.) |
|||
:<math>x=\sum_{i=1}^n x_i v_i,</math> |
|||
dan |
|||
:<math>\begin{align} |
|||
x&=\sum_{j=1}^n y_j w_j \\ |
|||
&=\sum_{j=1}^n y_j\sum_{i=1}^n a_{i,j}v_i\\ |
|||
&=\sum_{i=1}^n \left(\sum_{j=1}^n a_{i,j}y_j\right)v_i. |
|||
\end{align}</math> |
|||
Rumus perubahan basis kemudian dari keunikan dekomposisi vektor atas basis, di sini <math>B_\mathrm {old};</math> adalah |
|||
Barisan terurut <math>B_\mathrm {baru}=(w_1, \ldots, w_n) </math> disebut basis dari {{mvar|V}} jika dan hanya jika matriks <math>\mathbf{A}</math> [[Matriks terbalikkan|terbalikkan]], atau setara dengan itu, jika [[Determinan|determinannya]] tidak bernilai nol. Dalam kasus ini, <math>\mathbf{A}</math> disebut ''matriks perubahan basis'' dari basis <math>B_\mathrm{lama} </math> ke basis <math>B_\mathrm {baru}</math>. |
|||
:<math>x_i = \sum_{j=1}^n a_{i,j}y_j,</math> |
|||
untuk {{math|1=''i'' = 1, ..., ''n''}}. |
|||
== Lihat pula == |
|||
--- |
|||
* {{Annotated link|Perubahan basis}} |
|||
* {{Annotated link|Bingkai ruang vektor}} |
|||
* {{Annotated link|Basis bola}} |
|||
== Catatan == |
|||
Lebih lanjut, untuk sebarang vektor <math>z\in V,</math> misalkan <math>(x_1, \ldots, x_n) </math> adalah koordinat <math>z</math> atas <math>B_\mathrm{lama} </math>, dan <math>(y_1, \ldots, y_n) </math> adalah koordinatnya atas <math>B_\mathrm {baru}</math>, kita memiliki hubungan |
|||
{{Reflist}} |
|||
== Referensi == |
|||
<math>z=\sum_{i=1}^nx_iv_i = \sum_{j=1}^ny_jw_j.</math> |
|||
=== Referensi umum === |
|||
The ''change-of-basis formula'' expresses the coordinates over the old basis in term of the coordinates over the new basis. With above notation, it is |
|||
* {{Citation | last1=Blass | first1=Andreas | title=Axiomatic set theory | publisher=[[American Mathematical Society]] | location=Providence, R.I. | series=Contemporary Mathematics volume 31 | mr=763890 | year=1984 | chapter=Existence of bases implies the axiom of choice | pages=31–33|isbn=978-0-8218-5026-8}} |
|||
* {{Citation | last1=Brown | first1=William A. | title=Matrices and vector spaces | publisher=M. Dekker | location=New York | isbn=978-0-8247-8419-5 | year=1991|url=https://books.google.com/books?id=pFQYKlnW5Z0C}} |
|||
* {{Citation | last1=Lang | first1=Serge | author1-link=Serge Lang | title=Linear algebra | publisher=[[Springer-Verlag]] | location=Berlin, New York | isbn=978-0-387-96412-6 | year=1987}} |
|||
=== Referensi sejarah === |
|||
: <math>x_i = \sum_{j=1}^n a_{i,j}y_j\qquad\text{for } i=1, \ldots, n.</math> |
|||
* {{Citation | last1=Banach | first1=Stefan | author1-link=Stefan Banach | title=Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations) | url=http://matwbn.icm.edu.pl/ksiazki/fm/fm3/fm3120.pdf | year=1922 | journal=[[Fundamenta Mathematicae]] | issn=0016-2736 | volume=3| pages=133–181 |language=fr| doi=10.4064/fm-3-1-133-181 }} |
|||
* {{Citation | last1=Bolzano | first1=Bernard | author1-link=Bernard Bolzano | title=Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) | url=http://dml.cz/handle/10338.dmlcz/400338 | year=1804|language=de}} |
|||
* {{Citation | last1=Bourbaki | first1=Nicolas | author1-link=Nicolas Bourbaki | title=Éléments d'histoire des mathématiques (Elements of history of mathematics) | publisher=Hermann | location=Paris | year=1969|language=fr}} |
|||
* {{Citation | last1=Dorier | first1=Jean-Luc | title=A general outline of the genesis of vector space theory | mr=1347828 | year=1995 | journal=[[Historia Mathematica]] | volume=22 | issue=3 | pages=227–261 | doi=10.1006/hmat.1995.1024| url=http://archive-ouverte.unige.ch/unige:16642 }} |
|||
* {{Citation | last1=Fourier | first1=Jean Baptiste Joseph | author1-link=Joseph Fourier | title=Théorie analytique de la chaleur | url=https://books.google.com/books?id=TDQJAAAAIAAJ | publisher=Chez Firmin Didot, père et fils | year=1822|language=fr}} |
|||
* {{Citation | last1=Grassmann | first1=Hermann | author1-link=Hermann Grassmann | title=Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik | url=https://books.google.com/books?id=bKgAAAAAMAAJ&pg=PA1| year=1844|language=de}}, reprint: {{Citation | others=Kannenberg, L.C. | title=Extension Theory | publisher=[[American Mathematical Society]] | location=Providence, R.I. | isbn=978-0-8218-2031-5 | year=2000 | author=Hermann Grassmann. Translated by Lloyd C. Kannenberg.}} |
|||
* {{Citation | last1=Hamilton | first1=William Rowan | author1-link=William Rowan Hamilton | title=Lectures on Quaternions | url=http://historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=05230001&seq=9 | publisher=Royal Irish Academy | year=1853}} |
|||
* {{Citation |last1=Möbius |first1=August Ferdinand |author1-link=August Ferdinand Möbius |title=Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) |url=http://mathdoc.emath.fr/cgi-bin/oeitem?id=OE_MOBIUS__1_1_0 |year=1827 |language=de |url-status=dead |archiveurl=https://web.archive.org/web/20090412013616/http://mathdoc.emath.fr/cgi-bin/oeitem?id=OE_MOBIUS__1_1_0 |archivedate=2009-04-12 }} |
|||
* {{Citation | last1=Moore | first1=Gregory H. | title=The axiomatization of linear algebra: 1875–1940 | year=1995 | journal=[[Historia Mathematica]] | volume=22 | issue=3 | pages=262–303 | doi=10.1006/hmat.1995.1025}} |
|||
* {{Citation | last1=Peano | first1=Giuseppe | author1-link=Giuseppe Peano | title=Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva | year=1888 | location=Turin|language=it}} |
|||
In terms of matrices, the change of basis formula is |
|||
{{Aljabar linear}}{{short description|Set of vectors used to define coordinates}}{{redirect|Basis vector|basis vector in the context of crystals|Crystal structure|a more general concept in physics|Frame of reference}}{{redirect|Basis (mathematics)||Basis (disambiguation)#Mathematics{{!}}Basis}} |
|||
: <math>\mathbf x = A\,\mathbf y,</math> |
|||
[[Berkas:3d_two_bases_same_vector.svg|jmpl|229x229px|The same vector can be represented in two different bases (purple and red arrows).]] |
|||
In [[mathematics]], a [[Set (mathematics)|set]] {{mvar|B}} of vectors in a [[vector space]] {{math|''V''}} is called a '''basis''' ({{plural form}}: '''bases''') if every element of {{math|''V''}} may be written in a unique way as a finite [[linear combination]] of elements of {{mvar|B}}. The coefficients of this linear combination are referred to as '''components''' or '''coordinates''' of the vector with respect to {{mvar|B}}. The elements of a basis are called '''{{visible anchor|basis vectors}}'''. |
|||
Equivalently, a set {{mvar|B}} is a basis if its elements are [[linearly independent]] and every element of {{mvar|V}} is a [[linear combination]] of elements of {{mvar|B}}.<ref>{{cite book|last=Halmos|first=Paul Richard|year=1987|url=https://books.google.com/books?id=mdWeEhA17scC&pg=PA10|title=Finite-Dimensional Vector Spaces|location=New York|publisher=Springer|isbn=978-0-387-90093-3|edition=4th|page=10|author-link=Paul Halmos}}</ref> In other words, a basis is a linearly independent [[spanning set]]. |
|||
where <math>\mathbf x</math> and <math>\mathbf y</math> are the column vectors of the coordinates of {{mvar|z}} over <math>B_\mathrm {old}</math> and <math>B_\mathrm {new},</math> respectively. |
|||
A vector space can have several bases; however all the bases have the same number of elements, called the [[Dimension (vector space)|''dimension'' of the vector space]]. |
|||
''Proof:'' Using the above definition of the change-of basis matrix, one has |
|||
This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces. |
|||
: <math>\begin{align} |
|||
z&=\sum_{j=1}^n y_jw_j\\ |
|||
&=\sum_{j=1}^n \left(y_j\sum_{i=1}^n a_{i,j}v_i\right)\\ |
|||
&=\sum_{i=1}^n \left(\sum_{j=1}^n a_{i,j} y_j \right) v_i. |
|||
\end{align}</math> |
|||
== Definition == |
|||
As <math>z=\textstyle \sum_{i=1}^n x_iv_i,</math> the change-of-basis formula results from the uniqueness of the decomposition of a vector over a basis. |
|||
A '''basis''' {{math|''B''}} of a [[vector space]] {{math|''V''}} over a [[Field (mathematics)|field]] {{math|''F''}} (such as the [[real numbers]] {{math|'''R'''}} or the [[Complex number|complex numbers]] {{math|'''C'''}}) is a linearly independent [[subset]] of {{math|''V''}} that [[Linear span|spans]] {{math|''V''}}. This means that a subset {{mvar|B}} of {{math|''V''}} is a basis if it satisfies the two following conditions: |
|||
; ''linear independence'' |
|||
: |
|||
: for every [[Finite set|finite]] subset <math>\{\mathbf v_1, \dotsc, \mathbf v_m\}</math> of {{mvar|B}}, if <math>c_1 \mathbf v_1 + \cdots + c_m \mathbf v_m = \mathbf 0</math> for some <math>c_1,\dotsc,c_m</math> in {{math|''F''}}, then {{nowrap|<math>c_1 = \cdots = c_m = 0</math>;}} |
|||
; ''spanning property'' |
|||
: for every vector {{math|'''v'''}} in {{math|''V''}}, one can choose <math>a_1,\dotsc,a_n</math> in {{math|''F''}} and <math>\mathbf v_1, \dotsc, \mathbf v_n</math> in {{mvar|B}} such that {{nowrap|<math>\mathbf v = a_1 \mathbf v_1 + \cdots + a_n \mathbf v_n</math>.}} |
|||
The [[Scalar (mathematics)|scalars]] <math>a_i</math> are called the coordinates of the vector {{math|'''v'''}} with respect to the basis {{math|''B''}}, and by the first property they are uniquely determined. |
|||
== In terms of linear maps == |
|||
Normally, a [[Matrix (mathematics)|matrix]] represents a [[linear map]], and the product of a matrix and a column vector represents the [[function application]] of the corresponding linear map to the vector whose coordinates form the column vector. The change-of-basis formula is a specific case of this general principle, although this is not immediately clear from its definition and proof. |
|||
A vector space that has a [[Finite set|finite]] basis is called [[Dimension (vector space)|finite-dimensional]]. In this case, the finite subset can be taken as {{math|''B''}} itself to check for linear independence in the above definition. |
|||
When one says that a matrix ''represents'' a linear map, one refers implicitly to [[Basis (linear algebra)|bases]] of implied vector spaces, and to the fact that the choice of a basis induces an [[Linear isomorphism|isomorphism]] between a vector space and {{math|''F''{{sup|''n''}}}}, where {{mvar|F}} is the field of scalars. When only one basis is considered for each vector space, it is worth to leave this isomorphism implicit, and to work [[up to]] an isomorphism. As several bases of the same vector space are considered here, a more accurate wording is required. |
|||
It is often convenient or even necessary to have an [[Total order|ordering]] on the basis vectors, for example, when discussing [[Orientation (vector space)|orientation]], or when one considers the scalar coefficients of a vector with respect to a basis without referring explicitly to the basis elements. In this case, the ordering is necessary for associating each coefficient to the corresponding basis element. This ordering can be done by numbering the basis elements. In order to emphasize that an order has been chosen, one speaks of an '''ordered basis''', which is therefore not simply an unstructured [[Set (mathematics)|set]], but a [[sequence]], an [[indexed family]], or similar; see {{slink||Ordered bases and coordinates}} below. |
|||
Let {{mvar|F}} be a [[Field (mathematics)|field]], the set <math>F^n</math> of the [[Tuple|{{mvar|n}}-tuples]] is a {{mvar|F}}-vector space whose addition and scalar multiplication are defined component-wise. Its [[standard basis]] is the basis that has as its {{mvar|i}}th element the tuple with all components equal to {{math|0}} except the {{mvar|i}}th that is {{math|1}}. |
|||
== Examples == |
|||
A basis <math>B=(v_1, \ldots, v_n)</math> of a {{mvar|F}}-vector space {{mvar|V}} defines a [[linear isomorphism]] <math>\phi\colon F^n\to V</math> by |
|||
[[Berkas:Basis_graph_(no_label).svg|jmpl|400x400px|This picture illustrates the [[standard basis]] in '''R'''<sup>2</sup>. The blue and orange vectors are the elements of the basis; the green vector can be given in terms of the basis vectors, and so is [[linearly dependent]] upon them.]] |
|||
The set {{math|'''R'''<sup>2</sup>}} of the [[Ordered pair|ordered pairs]] of [[Real number|real numbers]] is a vector space under the operations of component-wise addition<math display="block">(a, b) + (c, d) = (a + c, b+d)</math>and scalar multiplication<math display="block">\lambda (a,b) = (\lambda a, \lambda b),</math>where <math>\lambda</math> is any real number. A simple basis of this vector space consists of the two vectors {{math|1='''e'''<sub>1</sub> = (1, 0)}} and {{math|1='''e'''<sub>2</sub> = (0, 1)}}. These vectors form a basis (called the [[standard basis]]) because any vector {{math|1='''v''' = (''a'', ''b'')}} of {{math|'''R'''<sup>2</sup>}} may be uniquely written as<math display="block">\mathbf v = a \mathbf e_1 + b \mathbf e_2.</math>Any other pair of linearly independent vectors of {{math|'''R'''<sup>2</sup>}}, such as {{math|(1, 1)}} and {{math|(−1, 2)}}, forms also a basis of {{math|'''R'''<sup>2</sup>}}. More generally, if {{mvar|F}} is a [[Field (mathematics)|field]], the set <math>F^n</math> of [[Tuple|{{mvar|n}}-tuples]] of elements of {{mvar|F}} is a vector space for similarly defined addition and scalar multiplication. Let<math display="block">\mathbf e_i = (0, \ldots, 0,1,0,\ldots, 0)</math>be the {{mvar|n}}-tuple with all components equal to 0, except the {{mvar|i}}th, which is 1. Then <math>\mathbf e_1, \ldots, \mathbf e_n</math> is a basis of <math>F^n,</math> which is called the ''standard basis'' of <math>F^n.</math> A different flavor of example is given by [[Polynomial ring|polynomial rings]]. If {{mvar|F}} is a field, the collection {{math|''F''[''X'']}} of all [[Polynomial|polynomials]] in one [[Indeterminate (variable)|indeterminate]] {{mvar|X}} with coefficients in {{mvar|F}} is an {{mvar|F}}-vector space. One basis for this space is the [[monomial basis]] {{mvar|B}}, consisting of all [[Monomial|monomials]]:<math display="block">B=\{1, X, X^2, \ldots\}.</math>Any set of polynomials such that there is exactly one polynomial of each degree (such as the [[Bernstein polynomial|Bernstein basis polynomials]] or [[Chebyshev polynomials]]) is also a basis. (Such a set of polynomials is called a [[polynomial sequence]].) But there are also many bases for {{math|''F''[''X'']}} that are not of this form. |
|||
== Properties == |
|||
: <math>\phi(x_1,\ldots,x_n)=\sum_{i=1}^n x_i v_i.</math> |
|||
Many properties of finite bases result from the [[Steinitz exchange lemma]], which states that, for any vector space {{mvar|V}}, given a finite [[spanning set]] {{mvar|S}} and a [[linearly independent]] set {{mvar|L}} of {{mvar|n}} elements of {{mvar|V}}, one may replace {{mvar|n}} well-chosen elements of {{mvar|S}} by the elements of {{mvar|L}} to get a spanning set containing {{mvar|L}}, having its other elements in {{mvar|S}}, and having the same number of elements as {{mvar|S}}. |
|||
Most properties resulting from the Steinitz exchange lemma remain true when there is no finite spanning set, but their proofs in the infinite case generally require the [[axiom of choice]] or a weaker form of it, such as the [[ultrafilter lemma]]. |
|||
Conversely, such a linear isomorphism defines a basis, which is the image by <math>\phi</math> of the standard basis of <math>F^n.</math> |
|||
If {{mvar|V}} is a vector space over a field {{mvar|F}}, then: |
|||
Let <math>B_\mathrm {old}=(v_1, \ldots, v_n)</math> be the "old basis" of a change of basis, and <math>\phi_\mathrm {old}</math> the associated isomorphism. Given a change-of basis matrix {{mvar|A}}, one could consider it the matrix of an [[endomorphism]] <math>\psi_A</math> of <math>F^n.</math> Finally, define |
|||
* If {{mvar|L}} is a linearly independent subset of a spanning set {{math|''S'' ⊆ ''V''}}, then there is a basis {{mvar|B}} such that <math display="block">L\subseteq B\subseteq S.</math> |
|||
: <math>\phi_\mathrm{new}=\phi_\mathrm{old}\circ\psi_A</math> |
|||
* {{mvar|V}} has a basis (this is the preceding property with {{mvar|L}} being the [[empty set]], and {{math|1=''S'' = ''V''}}). |
|||
* All bases of {{mvar|V}} have the same [[cardinality]], which is called the [[Dimension (vector space)|dimension]] of {{mvar|V}}. This is the [[Dimension theorem for vector spaces|dimension theorem]]. |
|||
* A generating set {{mvar|S}} is a basis of {{mvar|V}} if and only if it is minimal, that is, no [[Subset|proper subset]] of {{mvar|S}} is also a generating set of {{mvar|V}}. |
|||
* A linearly independent set {{mvar|L}} is a basis if and only if it is maximal, that is, it is not a proper subset of any linearly independent set. |
|||
If {{mvar|V}} is a vector space of dimension {{mvar|n}}, then: |
|||
(where <math>\circ</math> denotes [[function composition]]), and |
|||
* A subset of {{mvar|V}} with {{mvar|n}} elements is a basis if and only if it is linearly independent. |
|||
: <math>B_\mathrm{new}= \phi_\mathrm{new}(\phi_\mathrm{old}^{-1}(B_\mathrm{old})). </math> |
|||
* A subset of {{mvar|V}} with {{mvar|n}} elements is a basis if and only if it is a spanning set of {{mvar|V}}. |
|||
== Coordinates {{anchor|Ordered bases and coordinates}} == |
|||
A straightforward verification shows that this definition of <math>B_\mathrm{new}</math> is the same as that of the preceding section. |
|||
Let {{mvar|V}} be a vector space of finite dimension {{mvar|n}} over a field {{mvar|F}}, and<math display="block">B = \{\mathbf b_1, \ldots, \mathbf b_n\}</math>be a basis of {{mvar|V}}. By definition of a basis, every {{math|'''v'''}} in {{mvar|V}} may be written, in a unique way, as<math display="block">\mathbf v = \lambda_1 \mathbf b_1 + \cdots + \lambda_n \mathbf b_n,</math>where the coefficients <math>\lambda_1, \ldots, \lambda_n</math> are scalars (that is, elements of {{mvar|F}}), which are called the ''coordinates'' of {{math|'''v'''}} over {{mvar|B}}. However, if one talks of the ''set'' of the coefficients, one loses the correspondence between coefficients and basis elements, and several vectors may have the same ''set'' of coefficients. For example, <math>3 \mathbf b_1 + 2 \mathbf b_2</math> and <math>2 \mathbf b_1 + 3 \mathbf b_2</math> have the same set of coefficients {{math|{2, 3}<nowiki/>}}, and are different. It is therefore often convenient to work with an '''ordered basis'''; this is typically done by [[Index set|indexing]] the basis elements by the first natural numbers. Then, the coordinates of a vector form a [[Sequence (mathematics)|sequence]] similarly indexed, and a vector is completely characterized by the sequence of coordinates. An ordered basis is also called a '''frame''', a word commonly used, in various contexts, for referring to a sequence of data allowing defining coordinates. |
|||
Let, as usual, <math>F^n</math> be the set of the [[Tuple|{{mvar|n}}-tuples]] of elements of {{mvar|F}}. This set is an {{mvar|F}}-vector space, with addition and scalar multiplication defined component-wise. The map<math display="block">\varphi: (\lambda_1, \ldots, \lambda_n) \mapsto \lambda_1 \mathbf b_1 + \cdots + \lambda_n \mathbf b_n</math>is a [[linear isomorphism]] from the vector space <math>F^n</math> onto {{mvar|V}}. In other words, <math>F^n</math> is the [[coordinate space]] of {{mvar|V}}, and the {{mvar|n}}-tuple <math>\varphi^{-1}(\mathbf v)</math> is the [[coordinate vector]] of {{math|'''v'''}}. |
|||
Now, by composing the equation <math>\phi_\mathrm{new}=\phi_\mathrm{old}\circ\psi_A</math> with <math>\phi_\mathrm{old}^{-1}</math> on the left and <math>\phi_\mathrm{new}^{-1}</math> on the right, one gets |
|||
The [[inverse image]] by <math>\varphi</math> of <math>\mathbf b_i</math> is the {{mvar|n}}-tuple <math>\mathbf e_i</math> all of whose components are 0, except the {{mvar|i}}th that is 1. The <math>\mathbf e_i</math> form an ordered basis of <math>F^n</math>, which is called its [[standard basis]] or [[canonical basis]]. The ordered basis {{mvar|B}} is the image by <math>\varphi</math> of the canonical basis of {{nowrap|<math>F^n</math>.}} |
|||
: <math>\phi_\mathrm{old}^{-1} = \psi_A \circ \phi_\mathrm{new}^{-1}.</math> |
|||
It follows from what precedes that every ordered basis is the image by a linear isomorphism of the canonical basis of {{nowrap|<math>F^n</math>,}} and that every linear isomorphism from <math>F^n</math> onto {{mvar|V}} may be defined as the isomorphism that maps the canonical basis of <math>F^n</math> onto a given ordered basis of {{mvar|V}}. In other words, it is equivalent to define an ordered basis of {{mvar|V}}, or a linear isomorphism from <math>F^n</math> onto {{mvar|V}}. |
|||
It follows that, for <math>v\in V,</math> one has |
|||
== Change of basis == |
|||
: <math>\phi_\mathrm{old}^{-1}(v)= \psi_A(\phi_\mathrm{new}^{-1}(v)),</math> |
|||
{{main|Change of basis}} |
|||
Let {{math|''V''}} be a vector space of dimension {{mvar|n}} over a field {{math|''F''}}. Given two (ordered) bases <math>B_\text{old} = (\mathbf v_1, \ldots, \mathbf v_n)</math> and <math>B_\text{new} = (\mathbf w_1, \ldots, \mathbf w_n)</math> of {{math|''V''}}, it is often useful to express the coordinates of a vector {{mvar|x}} with respect to <math>B_\mathrm{old}</math> in terms of the coordinates with respect to <math>B_\mathrm{new}.</math> This can be done by the ''change-of-basis formula'', that is described below. The subscripts "old" and "new" have been chosen because it is customary to refer to <math>B_\mathrm{old}</math> and <math>B_\mathrm{new}</math> as the ''old basis'' and the ''new basis'', respectively. It is useful to describe the old coordinates in terms of the new ones, because, in general, one has [[Expression (mathematics)|expressions]] involving the old coordinates, and if one wants to obtain equivalent expressions in terms of the new coordinates; this is obtained by replacing the old coordinates by their expressions in terms of the new coordinates. |
|||
Typically, the new basis vectors are given by their coordinates over the old basis, that is,<math display="block">\mathbf w_j = \sum_{i=1}^n a_{i,j} \mathbf v_i.</math>If <math>(x_1, \ldots, x_n)</math> and <math>(y_1, \ldots, y_n)</math> are the coordinates of a vector {{math|'''x'''}} over the old and the new basis respectively, the change-of-basis formula is<math display="block">x_i = \sum_{j=1}^n a_{i,j}y_j,</math>for {{math|1=''i'' = 1, ..., ''n''}}. |
|||
which is the change-of-basis formula expressed in terms of linear maps instead of coordinates. |
|||
This formula may be concisely written in [[Matrix (mathematics)|matrix]] notation. Let {{mvar|A}} be the matrix of the {{nowrap|<math>a_{i,j}</math>,}} and<math display="block">X= \begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix} \quad \text{and} \quad Y = \begin{bmatrix} y_1 \\ \vdots \\ y_n \end{bmatrix}</math>be the [[Column vector|column vectors]] of the coordinates of {{math|'''v'''}} in the old and the new basis respectively, then the formula for changing coordinates is<math display="block">X = A Y.</math>The formula can be proven by considering the decomposition of the vector {{math|'''x'''}} on the two bases: one has<math display="block">\mathbf x = \sum_{i=1}^n x_i \mathbf v_i,</math>and<math display="block">\mathbf x =\sum_{j=1}^n y_j \mathbf w_j |
|||
== Function defined on a vector space == |
|||
= \sum_{j=1}^n y_j\sum_{i=1}^n a_{i,j}\mathbf v_i |
|||
A [[Function (mathematics)|function]] that has a vector space as its [[Domain of a function|domain]] is commonly specified as a [[multivariate function]] whose variables are the coordinates on some basis of the vector on which the function is [[Function application|applied]]. |
|||
= \sum_{i=1}^n \biggl(\sum_{j=1}^n a_{i,j}y_j\biggr)\mathbf v_i.</math>The change-of-basis formula results then from the uniqueness of the decomposition of a vector over a basis, here {{nowrap|<math>B_\text{old}</math>;}} that is<math display="block">x_i = \sum_{j=1}^n a_{i,j} y_j,</math>for {{math|1=''i'' = 1, ..., ''n''}}. |
|||
== Related notions == |
|||
When the basis is changed, the [[Expression (mathematics)|expression]] of the function is changed. This change can be computed by substituting the "old" coordinates for their expressions in terms of the "new" coordinates. More precisely, if {{math|''f''('''x''')}} is the expression of the function in terms of the old coordinates, and if {{math|'''x''' {{=}} ''A'''''y'''}} is the change-of-base formula, then {{math|''f''(''A'''''y''')}} is the expression of the same function in terms of the new coordinates. |
|||
=== Free module === |
|||
The fact that the change-of-basis formula expresses the old coordinates in terms of the new one may seem unnatural, but appears as useful, as no [[matrix inversion]] is needed here. |
|||
{{main|Free module|Free abelian group}} |
|||
If one replaces the field occurring in the definition of a vector space by a [[Ring (mathematics)|ring]], one gets the definition of a [[Module (mathematics)|module]]. For modules, [[linear independence]] and [[Spanning set|spanning sets]] are defined exactly as for vector spaces, although "[[Generating set of a module|generating set]]" is more commonly used than that of "spanning set". |
|||
Like for vector spaces, a ''basis'' of a module is a linearly independent subset that is also a generating set. A major difference with the theory of vector spaces is that not every module has a basis. A module that has a basis is called a ''free module''. Free modules play a fundamental role in module theory, as they may be used for describing the structure of non-free modules through [[Free resolution|free resolutions]]. |
|||
As the change-of-basis formula involves only [[Linear function|linear functions]], many function properties are kept by a change of basis. This allows defining these properties as properties of functions of a variable vector that are not related to any specific basis. So, a function whose domain is a vector space or a subset of it is |
|||
A module over the integers is exactly the same thing as an [[abelian group]]. Thus a free module over the integers is also a free abelian group. Free abelian groups have specific properties that are not shared by modules over other rings. Specifically, every subgroup of a free abelian group is a free abelian group, and, if {{mvar|G}} is a subgroup of a finitely generated free abelian group {{mvar|H}} (that is an abelian group that has a finite basis), then there is a basis <math>\mathbf e_1, \ldots, \mathbf e_n</math> of {{mvar|H}} and an integer {{math|0 ≤ ''k'' ≤ ''n''}} such that <math>a_1 \mathbf e_1, \ldots, a_k \mathbf e_k</math> is a basis of {{mvar|G}}, for some nonzero integers {{nowrap|<math>a_1, \ldots, a_k</math>.}} For details, see {{slink|Free abelian group|Subgroups}}. |
|||
* a linear function, |
|||
* a [[polynomial function]], |
|||
* a [[continuous function]], |
|||
* a [[differentiable function]], |
|||
* a [[smooth function]], |
|||
* an [[analytic function]], |
|||
=== Analysis === |
|||
if the multivariate function that represents it on some basis—and thus on every basis—has the same property. |
|||
In the context of infinite-dimensional vector spaces over the real or complex numbers, the term '''{{visible anchor|Hamel basis}}''' (named after [[Georg Hamel]]<ref>{{Harvnb|Hamel|1905}}</ref>) or '''algebraic basis''' can be used to refer to a basis as defined in this article. This is to make a distinction with other notions of "basis" that exist when infinite-dimensional vector spaces are endowed with extra structure. The most important alternatives are [[Orthogonal basis|orthogonal bases]] on [[Hilbert space|Hilbert spaces]], [[Schauder basis|Schauder bases]], and [[Markushevich basis|Markushevich bases]] on [[Normed linear space|normed linear spaces]]. In the case of the real numbers '''R''' viewed as a vector space over the field '''Q''' of rational numbers, Hamel bases are uncountable, and have specifically the [[cardinality]] of the continuum, which is the [[cardinal number]] {{nowrap|<math>2^{\aleph_0}</math>,}} where <math>\aleph_0</math> ([[aleph-nought]]) is the smallest infinite cardinal, the cardinal of the integers. |
|||
The common feature of the other notions is that they permit the taking of infinite linear combinations of the basis vectors in order to generate the space. This, of course, requires that infinite sums are meaningfully defined on these spaces, as is the case for [[Topological vector space|topological vector spaces]] – a large class of vector spaces including e.g. [[Hilbert space|Hilbert spaces]], [[Banach space|Banach spaces]], or [[Fréchet space|Fréchet spaces]]. |
|||
This is specially useful in the theory of [[Manifold|manifolds]], as this allows extending the concepts of continuous, differentiable, smooth and analytic functions to functions that are defined on a manifold. |
|||
The preference of other types of bases for infinite-dimensional spaces is justified by the fact that the Hamel basis becomes "too big" in Banach spaces: If ''X'' is an infinite-dimensional normed vector space that is [[Complete space|complete]] (i.e. ''X'' is a [[Banach space]]), then any Hamel basis of ''X'' is necessarily [[uncountable]]. This is a consequence of the [[Baire category theorem]]. The completeness as well as infinite dimension are crucial assumptions in the previous claim. Indeed, finite-dimensional spaces have by definition finite bases and there are infinite-dimensional (''non-complete'') normed spaces that have countable Hamel bases. Consider {{nowrap|<math>c_{00}</math>,}} the space of the [[Sequence|sequences]] <math>x=(x_n)</math> of real numbers that have only finitely many non-zero elements, with the norm {{nowrap|<math display="inline">\|x\|=\sup_n |x_n|</math>.}} Its [[standard basis]], consisting of the sequences having only one non-zero element, which is equal to 1, is a countable Hamel basis. |
|||
== Linear maps == |
|||
Consider a [[linear map]] {{math|''T'': ''W'' → ''V''}} from a [[vector space]] {{mvar|W}} of dimension {{mvar|n}} to a vector space {{mvar|V}} of dimension {{mvar|m}}. It is represented on "old" bases of {{mvar|V}} and {{mvar|W}} by a {{math|''m''×''n''}} matrix {{mvar|M}}. A change of bases is defined by an {{math|''m''×''m''}} change-of-basis matrix {{mvar|P}} for {{mvar|V}}, and an {{math|''n''×''n''}} change-of-basis matrix {{mvar|Q}} for {{mvar|W}}. |
|||
==== Example ==== |
|||
On the "new" bases, the matrix of {{mvar|T}} is |
|||
In the study of [[Fourier series]], one learns that the functions {{math|1={1} ∪ { sin(''nx''), cos(''nx'') : ''n'' = 1, 2, 3, ... }<nowiki/>}} are an "orthogonal basis" of the (real or complex) vector space of all (real or complex valued) functions on the interval [0, 2π] that are square-integrable on this interval, i.e., functions ''f'' satisfying<math display="block">\int_0^{2\pi} \left|f(x)\right|^2\,dx < \infty.</math>The functions {{math|1={1} ∪ { sin(''nx''), cos(''nx'') : ''n'' = 1, 2, 3, ... }<nowiki/>}} are linearly independent, and every function ''f'' that is square-integrable on [0, 2π] is an "infinite linear combination" of them, in the sense that<math display="block">\lim_{n\to\infty} \int_0^{2\pi} \biggl|a_0 + \sum_{k=1}^n \left(a_k\cos\left(kx\right)+b_k\sin\left(kx\right)\right)-f(x)\biggr|^2 dx = 0</math>for suitable (real or complex) coefficients ''a<sub>k</sub>'', ''b<sub>k</sub>''. But many<ref>Note that one cannot say "most" because the cardinalities of the two sets (functions that can and cannot be represented with a finite number of basis functions) are the same.</ref> square-integrable functions cannot be represented as ''finite'' linear combinations of these basis functions, which therefore ''do not'' comprise a Hamel basis. Every Hamel basis of this space is much bigger than this merely countably infinite set of functions. Hamel bases of spaces of this kind are typically not useful, whereas [[orthonormal bases]] of these spaces are essential in [[Fourier analysis]]. |
|||
=== Geometry === |
|||
: <math>P^{-1}MQ.</math> |
|||
The geometric notions of an [[affine space]], [[projective space]], [[convex set]], and [[Cone (linear algebra)|cone]] have related notions of {{anchor|affine basis}} ''basis''.<ref>{{cite book|last=Rees|first=Elmer G.|year=2005|url=https://books.google.com/books?id=JkzPRaihGIYC&pg=PA7|title=Notes on Geometry|location=Berlin|publisher=Springer|isbn=978-3-540-12053-7|page=7}}</ref> An '''affine basis''' for an ''n''-dimensional affine space is <math>n+1</math> points in [[general linear position]]. A '''{{visible anchor|projective basis}}''' is <math>n+2</math> points in general position, in a projective space of dimension ''n''. A '''{{visible anchor|convex basis}}''' of a [[polytope]] is the set of the vertices of its [[convex hull]]. A '''{{visible anchor|cone basis}}'''<ref>{{cite journal|last=Kuczma|first=Marek|year=1970|title=Some remarks about additive functions on cones|journal=[[Aequationes Mathematicae]]|volume=4|issue=3|pages=303–306|doi=10.1007/BF01844160|s2cid=189836213}}</ref> consists of one point by edge of a polygonal cone. See also a [[Hilbert basis (linear programming)]]. |
|||
=== Random basis === |
|||
This is a straightforward consequence of the change-of-basis formula. |
|||
For a [[probability distribution]] in {{math|'''R'''<sup>''n''</sup>}} with a [[probability density function]], such as the equidistribution in an ''n''-dimensional ball with respect to Lebesgue measure, it can be shown that {{mvar|n}} randomly and independently chosen vectors will form a basis [[with probability one]], which is due to the fact that {{mvar|n}} linearly dependent vectors {{math|'''x'''<sub>1</sub>}}, ..., {{math|'''x'''<sub>''n''</sub>}} in {{math|'''R'''<sup>''n''</sup>}} should satisfy the equation {{math|1=det['''x'''<sub>1</sub> ⋯ '''x'''<sub>''n''</sub>] = 0}} (zero determinant of the matrix with columns {{math|'''x'''<sub>''i''</sub>}}), and the set of zeros of a non-trivial polynomial has zero measure. This observation has led to techniques for approximating random bases.<ref>{{cite journal|last1=Igelnik|first1=B.|last2=Pao|first2=Y.-H.|year=1995|title=Stochastic choice of basis functions in adaptive function approximation and the functional-link net|journal=IEEE Trans. Neural Netw.|volume=6|issue=6|pages=1320–1329|doi=10.1109/72.471375|pmid=18263425}}</ref><ref name="GorbanTyukin2016">{{cite journal|last1=Gorban|first1=Alexander N.|last2=Tyukin|first2=Ivan Y.|last3=Prokhorov|first3=Danil V.|last4=Sofeikov|first4=Konstantin I.|year=2016|title=Approximation with Random Bases: Pro et Contra|journal=[[Information Sciences (journal)|Information Sciences]]|volume=364-365|pages=129–145|arxiv=1506.04631|doi=10.1016/j.ins.2015.09.021|author1-link=Aleksandr Gorban|s2cid=2239376}}</ref> |
|||
[[Berkas:Random_almost_orthogonal_sets.png|jmpl|270x270px|Empirical distribution of lengths N of pairwise almost orthogonal chains of vectors that are independently randomly sampled from the ''n''-dimensional cube {{math|[−1, 1]<sup>''n''</sup>}} as a function of dimension, ''n''. Boxplots show the second and third quartiles of this data for each ''n'', red bars correspond to the medians, and blue stars indicate means. Red curve shows theoretical bound given by Eq. (1) and green curve shows a refined estimate.<ref name="GorbanTyukin2016" />]] |
|||
It is difficult to check numerically the linear dependence or exact orthogonality. Therefore, the notion of ε-orthogonality is used. For [[Inner product space|spaces with inner product]], ''x'' is ε-orthogonal to ''y'' if <math>\left|\left\langle x,y \right\rangle\right| / \left(\left\|x\right\|\left\|y\right\|\right) < \varepsilon</math> (that is, cosine of the angle between {{mvar|x}} and {{mvar|y}} is less than {{mvar|ε}}). |
|||
In high dimensions, two independent random vectors are with high probability almost orthogonal, and the number of independent random vectors, which all are with given high probability pairwise almost orthogonal, grows exponentially with dimension. More precisely, consider equidistribution in ''n''-dimensional ball. Choose ''N'' independent random vectors from a ball (they are [[Independent and identically distributed random variables|independent and identically distributed]]). Let ''θ'' be a small positive number. Then for{{NumBlk||<math display="block">N\leq {\exp}\bigl(\tfrac14\varepsilon^2n\bigr)\sqrt{-\ln(1-\theta)}</math>|Eq. 1}}{{mvar|N}} random vectors are all pairwise ε-orthogonal with probability {{math|1 − ''θ''}}.<ref name="GorbanTyukin2016" /> This {{mvar|N}} growth exponentially with dimension {{mvar|n}} and <math>N\gg n</math> for sufficiently big {{mvar|n}}. This property of random bases is a manifestation of the so-called {{em|measure concentration phenomenon}}.<ref>{{cite journal|last=Artstein|first=Shiri|author-link=Shiri Artstein|year=2002|title=Proportional concentration phenomena of the sphere|url=http://www.tau.ac.il/~shiri/israelj/ISRAJ.pdf|journal=[[Israel Journal of Mathematics]]|volume=132|issue=1|pages=337–358|doi=10.1007/BF02784520|doi-access=free|citeseerx=10.1.1.417.2375|s2cid=8095719}}</ref> |
|||
== Endomorphisms == |
|||
[[Endomorphism|Endomorphisms]], are linear maps from a vector space {{mvar|V}} to itself. For a change of basis, the formula of the preceding section applies, with the same change-of-basis matrix on both sides of the formula. That is, if {{mvar|M}} is the [[square matrix]] of an endomorphism of {{mvar|V}} over an "old" basis, and {{mvar|P}} is a change-of-basis matrix, then the matrix of the endomorphism on the "new" basis is |
|||
The figure (right) illustrates distribution of lengths N of pairwise almost orthogonal chains of vectors that are independently randomly sampled from the ''n''-dimensional cube {{math|[−1, 1]<sup>''n''</sup>}} as a function of dimension, ''n''. A point is first randomly selected in the cube. The second point is randomly chosen in the same cube. If the angle between the vectors was within {{math|π/2 ± 0.037π/2}} then the vector was retained. At the next step a new vector is generated in the same hypercube, and its angles with the previously generated vectors are evaluated. If these angles are within {{math|π/2 ± 0.037π/2}} then the vector is retained. The process is repeated until the chain of almost orthogonality breaks, and the number of such pairwise almost orthogonal vectors (length of the chain) is recorded. For each ''n'', 20 pairwise almost orthogonal chains were constructed numerically for each dimension. Distribution of the length of these chains is presented. |
|||
: <math>P^{-1}MP.</math> |
|||
== Proof that every vector space has a basis == |
|||
As every [[invertible matrix]] can be used as a change-of-basis matrix, this implies that two matrices are [[Similar matrices|similar]] if and only if they represent the same endomorphism on two different bases. |
|||
Let {{math|'''V'''}} be any vector space over some field {{math|'''F'''}}. Let {{math|'''X'''}} be the set of all linearly independent subsets of {{math|'''V'''}}. |
|||
The set {{math|'''X'''}} is nonempty since the empty set is an independent subset of {{math|'''V'''}}, and it is [[Partial order|partially ordered]] by inclusion, which is denoted, as usual, by {{math|⊆}}. |
|||
== Bilinear forms == |
|||
A ''[[bilinear form]]'' on a vector space ''V'' over a [[Field (mathematics)|field]] {{mvar|F}} is a function {{math|''V'' × ''V'' → F}} which is [[Linear map|linear]] in both arguments. That is, {{math|''B'' : ''V'' × ''V'' → F}} is bilinear if the maps <math>v \mapsto B(v, w)</math> and <math>v \mapsto B(w, v)</math> are linear for every fixed <math>w\in V.</math> |
|||
Let {{math|'''Y'''}} be a subset of {{math|'''X'''}} that is totally ordered by {{math|⊆}}, and let {{math|L<sub>'''Y'''</sub>}} be the union of all the elements of {{math|'''Y'''}} (which are themselves certain subsets of {{math|'''V'''}}). |
|||
Since {{math|('''Y''', ⊆)}} is totally ordered, every finite subset of {{math|L<sub>'''Y'''</sub>}} is a subset of an element of {{math|'''Y'''}}, which is a linearly independent subset of {{math|'''V'''}}, and hence {{math|L<sub>'''Y'''</sub>}} is linearly independent. Thus {{math|L<sub>'''Y'''</sub>}} is an element of {{math|'''X'''}}. Therefore, {{math|L<sub>'''Y'''</sub>}} is an upper bound for {{math|'''Y'''}} in {{math|('''X''', ⊆)}}: it is an element of {{math|'''X'''}}, that contains every element of {{math|'''Y'''}}. |
|||
: <math>B(v, w)=\mathbf v^{\mathsf T}\mathbf B\mathbf w,</math> |
|||
As {{math|'''X'''}} is nonempty, and every totally ordered subset of {{math|('''X''', ⊆)}} has an upper bound in {{math|'''X'''}}, [[Zorn's lemma]] asserts that {{math|'''X'''}} has a maximal element. In other words, there exists some element {{math|L<sub>'''max'''</sub>}} of {{math|'''X'''}} satisfying the condition that whenever {{math|L<sub>'''max'''</sub> ⊆ L}} for some element {{math|L}} of {{math|'''X'''}}, then {{math|1=L = L<sub>'''max'''</sub>}}. |
|||
where <math>\mathbf v^{\mathsf T}</math> denotes the [[transpose]] of the matrix {{math|'''v'''}}. |
|||
It remains to prove that {{math|L<sub>'''max'''</sub>}} is a basis of {{math|'''V'''}}. Since {{math|L<sub>'''max'''</sub>}} belongs to {{math|'''X'''}}, we already know that {{math|L<sub>'''max'''</sub>}} is a linearly independent subset of {{math|'''V'''}}. |
|||
If {{mvar|P}} is a change of basis matrix, then a straightforward computation shows that the matrix of the bilinear form on the new basis is |
|||
If there were some vector {{math|'''w'''}} of {{math|'''V'''}} that is not in the span of {{math|L<sub>'''max'''</sub>}}, then {{math|'''w'''}} would not be an element of {{math|L<sub>'''max'''</sub>}} either. Let {{math|1=L<sub>'''w'''</sub> = L<sub>'''max'''</sub> ∪ {'''w'''}<nowiki/>}}. This set is an element of {{math|'''X'''}}, that is, it is a linearly independent subset of {{math|'''V'''}} (because '''w''' is not in the span of {{math|L<sub>'''max'''</sub>}}, and {{math|L<sub>'''max'''</sub>}} is independent). As {{math|L<sub>'''max'''</sub> ⊆ L<sub>'''w'''</sub>}}, and {{math|L<sub>'''max'''</sub> ≠ L<sub>'''w'''</sub>}} (because {{math|L<sub>'''w'''</sub>}} contains the vector {{math|'''w'''}} that is not contained in {{math|L<sub>'''max'''</sub>}}), this contradicts the maximality of {{math|L<sub>'''max'''</sub>}}. Thus this shows that {{math|L<sub>'''max'''</sub>}} spans {{math|'''V'''}}. |
|||
: <math>P^{\mathsf T}\mathbf B P.</math> |
|||
Hence {{math|L<sub>'''max'''</sub>}} is linearly independent and spans {{math|'''V'''}}. It is thus a basis of {{math|'''V'''}}, and this proves that every vector space has a basis. |
|||
A [[symmetric bilinear form]] is a bilinear form {{mvar|B}} such that <math>B(v,w)=B(w,v)</math> for every {{mvar|v}} and {{mvar|w}} in {{mvar|V}}. It follows that the matrix of {{mvar|B}} on any basis is [[Symmetric matrix|symmetric]]. This implies that the property of being a symmetric matrix must be kept by the above change-of-base formula. One can also check this by noting that the transpose of a matrix product is the product of the transposes computed in the reverse order. In particular, |
|||
This proof relies on Zorn's lemma, which is equivalent to the [[axiom of choice]]. Conversely, it has been proved that if every vector space has a basis, then the axiom of choice is true.<ref>{{Harvnb|Blass|1984}}</ref> Thus the two assertions are equivalent. |
|||
: <math>(P^{\mathsf T}\mathbf B P)^{\mathsf T} = P^{\mathsf T}\mathbf B^{\mathsf T} P,</math> |
|||
and the two members of this equation equal <math>P^{\mathsf T} \mathbf B P</math> if the matrix {{math|'''B'''}} is symmetric. |
|||
If the [[Characteristic (algebra)|characteristic]] of the ground field {{mvar|F}} is not two, then for every symmetric bilinear form there is a basis for which the matrix is [[Diagonal matrix|diagonal]]. Moreover, the resulting nonzero entries on the diagonal are defined up to the multiplication by a square. So, if the ground field is the field <math>\mathbb R</math> of the [[Real number|real numbers]], these nonzero entries can be chosen to be either {{math|1}} or {{math|–1}}. [[Sylvester's law of inertia]] is a theorem that asserts that the numbers of {{math|1}} and of {{math|–1}} depends only on the bilinear form, and not of the change of basis. |
|||
Symmetric bilinear forms over the reals are often encountered in [[geometry]] and [[physics]], typically in the study of [[Quadric|quadrics]] and of the [[inertia]] of a [[rigid body]]. In these cases, [[orthonormal bases]] are specially useful; this means that one generally prefer to restrict changes of basis to those that have an [[Orthogonal matrix|orthogonal]] change-of-base matrix, that is, a matrix such that <math>P^{\mathsf T}=P^{-1}.</math> Such matrices have the fundamental property that the change-of-base formula is the same for a symmetric bilinear form and the endomorphism that is represented by the same symmetric matrix. The [[Spectral theorem]] asserts that, given such a symmetric matrix, there is an orthogonal change of basis such that the resulting matrix (of both the bilinear form and the endomorphism) is a diagonal matrix with the [[eigenvalues]] of the initial matrix on the diagonal. It follows that, over the reals, if the matrix of an endomorphism is symmetric, then it is [[Diagonalizable matrix|diagonalizable]]. |
|||
== See also == |
== See also == |
||
* [[ |
* [[Basis of a matroid]] |
||
* [[Basis of a linear program]] |
|||
* [[Covariance and contravariance of vectors]] |
|||
* {{Annotated link|Change of basis}} |
|||
* [[Integral transform]], the continuous analogue of change of basis. |
|||
* {{Annotated link|Frame of a vector space}} |
|||
* {{Annotated link|Spherical basis}} |
|||
== Notes == |
== Notes == |
||
{{ |
{{Reflist}} |
||
== References == |
== References == |
||
{{Reflist}} |
|||
=== General references === |
|||
== Bibliography == |
|||
* {{Citation | last1=Blass | first1=Andreas | title=Axiomatic set theory | publisher=[[American Mathematical Society]] | location=Providence, R.I. | series=Contemporary Mathematics volume 31 | mr=763890 | year=1984 | chapter=Existence of bases implies the axiom of choice | pages=31–33|isbn=978-0-8218-5026-8|chapter-url=http://www.math.lsa.umich.edu/~ablass/bases-AC.pdf}} |
|||
* {{Citation | last1=Brown | first1=William A. | title=Matrices and vector spaces | publisher=M. Dekker | location=New York | isbn=978-0-8247-8419-5 | year=1991|url=https://books.google.com/books?id=pFQYKlnW5Z0C}} |
|||
* {{Citation | last1=Lang | first1=Serge | author1-link=Serge Lang | title=Linear algebra | publisher=[[Springer-Verlag]] | location=Berlin, New York | isbn=978-0-387-96412-6 | year=1987}} |
|||
=== Historical references === |
|||
* {{Citation | last1=Banach | first1=Stefan | author1-link=Stefan Banach | title=Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations) | url=http://matwbn.icm.edu.pl/ksiazki/fm/fm3/fm3120.pdf | year=1922 | journal=[[Fundamenta Mathematicae]] | issn=0016-2736 | volume=3| pages=133–181 |language=fr| doi=10.4064/fm-3-1-133-181 }} |
|||
* {{citation|last1=Anton|first1=Howard|year=1987|isbn=0-471-84819-0|title=Elementary Linear Algebra|edition=5th|publisher=[[John Wiley & Sons|Wiley]]|location=New York}} |
|||
* {{Citation | last1=Bolzano | first1=Bernard | author1-link=Bernard Bolzano | title=Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) | url=http://dml.cz/handle/10338.dmlcz/400338 | year=1804|language=de}} |
|||
* {{citation|last1=Beauregard|first1=Raymond A.|last2=Fraleigh|first2=John B.|title=A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields|location=Boston|publisher=[[Houghton Mifflin Company]]|year=1973|isbn=0-395-14017-X|url-access=registration|url=https://archive.org/details/firstcourseinlin0000beau}} |
|||
* {{ |
* {{Citation | last1=Bourbaki | first1=Nicolas | author1-link=Nicolas Bourbaki | title=Éléments d'histoire des mathématiques (Elements of history of mathematics) | publisher=Hermann | location=Paris | year=1969|language=fr}} |
||
* {{Citation | last1=Dorier | first1=Jean-Luc | title=A general outline of the genesis of vector space theory | mr=1347828 | year=1995 | journal=[[Historia Mathematica]] | volume=22 | issue=3 | pages=227–261 | doi=10.1006/hmat.1995.1024| url=http://archive-ouverte.unige.ch/unige:16642 |doi-access=free}} |
|||
* {{Citation | last1=Fourier | first1=Jean Baptiste Joseph | author1-link=Joseph Fourier | title=Théorie analytique de la chaleur | url=https://books.google.com/books?id=TDQJAAAAIAAJ | publisher=Chez Firmin Didot, père et fils | year=1822|language=fr}} |
|||
* {{Citation | last1=Grassmann | first1=Hermann | author1-link=Hermann Grassmann | title=Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik | url=https://books.google.com/books?id=bKgAAAAAMAAJ&pg=PA1| year=1844|language=de}}, reprint: {{Citation | others=Kannenberg, L.C. | title=Extension Theory | publisher=[[American Mathematical Society]] | location=Providence, R.I. | isbn=978-0-8218-2031-5 | year=2000 | author=Hermann Grassmann. Translated by Lloyd C. Kannenberg.}} |
|||
* {{Citation|last=Hamel|first=Georg|author1-link=Georg Hamel|title=Eine Basis aller Zahlen und die unstetigen Lösungen der Funktionalgleichung f(x+y)=f(x)+f(y)|journal=Mathematische Annalen|location=Leipzig|volume=60|pages=459–462|url=http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002260395|year=1905|issue=3|doi=10.1007/BF01457624|s2cid=120063569|language=de}} |
|||
* {{Citation | last1=Hamilton | first1=William Rowan | author1-link=William Rowan Hamilton | title=Lectures on Quaternions | url=http://historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=05230001&seq=9 | publisher=Royal Irish Academy | year=1853}} |
|||
* {{Citation |last1=Möbius |first1=August Ferdinand |author1-link=August Ferdinand Möbius |title=Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) |url=http://mathdoc.emath.fr/cgi-bin/oeitem?id=OE_MOBIUS__1_1_0 |year=1827 |language=de |url-status=dead |archive-url=https://web.archive.org/web/20090412013616/http://mathdoc.emath.fr/cgi-bin/oeitem?id=OE_MOBIUS__1_1_0|archive-date=2009-04-12}} |
|||
* {{Citation | last1=Moore | first1=Gregory H. | title=The axiomatization of linear algebra: 1875–1940 | year=1995 | journal=[[Historia Mathematica]] | volume=22 | issue=3 | pages=262–303 | doi=10.1006/hmat.1995.1025|doi-access=free}} |
|||
* {{Citation | last1=Peano | first1=Giuseppe | author1-link=Giuseppe Peano | title=Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva | year=1888 | location=Turin|language=it}} |
|||
== External links == |
== External links == |
||
* Instructional videos from Khan Academy |
|||
* [http://ocw.mit.edu/courses/mathematics/18-06-linear-algebra-spring-2010/video-lectures/lecture-31-change-of-basis-image-compression/ MIT Linear Algebra Lecture on Change of Basis], from MIT OpenCourseWare |
|||
** [https://web.archive.org/web/20120426050335/http://khanexercises.appspot.com/video?v=zntNi3-ybfQ Introduction to bases of subspaces] |
|||
* [https://www.youtube.com/watch?v=1j5WnqwMdCk Khan Academy Lecture on Change of Basis], from Khan Academy |
|||
** [https://web.archive.org/web/20120426050418/http://khanexercises.appspot.com/video?v=Zn2K8UIT8r4 Proof that any subspace basis has same number of elements] |
|||
* {{Cite web|date=August 6, 2016|title=Linear combinations, span, and basis vectors|url=https://www.youtube.com/watch?v=k7RM-ot2NWY&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=3|work=Essence of linear algebra|archive-url=https://ghostarchive.org/varchive/youtube/20211117/k7RM-ot2NWY|archive-date=2021-11-17|via=[[YouTube]]|url-status=live}}{{cbignore}} |
|||
* {{springer|title=Basis|id=p/b015350}} |
|||
{{linear algebra}} |
{{linear algebra}} {{tensors}} |
||
[[Kategori:Aljabar linear]] |
|||
Revisi per 17 Maret 2024 03.52
Dalam aljabar linear, basis adalah himpunan vektor, yang dalam sebuah kombinasi linear dapat merepresentasikan setiap vektor dalam suatu ruang vektor. Tidak ada elemen dalam himpunan vektor tersebut yang dapat direpresentasikan sebagai kombinasi linear vektor-vektor lain. Basis juga dapat dianggap sebagai "sistem koordinat".[1]
Definisi formal
Basis untuk ruang vektor (atas medan ) adalah suatu himpunan bagian yang memenuhi:
- Setiap dapat dituliskan sebagai dengan .
- Jika representasi lain, maka dan ada suatu permutasi yang dan .
Contoh
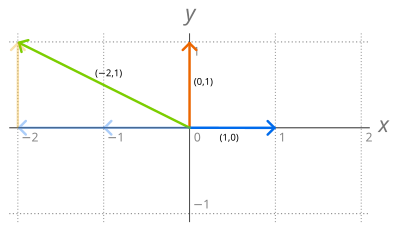
- Himpunan R2 dari pasangan terurut dari bilangan riil adalah ruang vektor untuk penjumlahan berdasarkan komponen
- dan perkalian skalar
- dimana adalah bilangan real apa pun. Basis sederhana dari ruang vektor ini, disebut basis standar terdiri dari dua vektor e1 = (1,0) and e2 = (0,1), karena vektor apapun v = (a, b) dari R2 dapat ditulis secara unik sebagai
- Pasangan vektor bebas linear lainnya R2, seperti (1, 1) dan (−1, 2), bentuk menjadi dasar R2.
- Lebih umum lagi, jika F adalah bidang, himpunan dari n-tupel dari elemen F adalah ruang vektor untuk penjumlahan dan perkalian skalar yang didefinisikan serupa. Karena
- jadilah tupel n dengan semua komponen sama dengan 0, kecuali i yaitu 1. Kemudian adalah basis dari yang disebut basis standar dari
- Jika F adalah bidang gelanggang polinomial F[X] dari polinomial dalam satu tak tentu memiliki basis B, yang disebut basis monomial, yang terdiri dari semua monomial:
- Kumpulan polinomial apa pun yang hanya ada satu polinomial pada setiap derajat juga merupakan basis. Kumpulan polinomial seperti itu disebut urutan polinomial. Contoh (di antara banyak) urutan polinomial tersebut adalah polinomial basis Bernstein, dan polinomial Chebyshev.
Koordinat
Misalkan V menjadi ruang vektor berdimensi berhingga n di atas bidang F, dan
menjadi dasar dari V. Menurut definisi basis, setiap v pada V dapat ditulis, dengan cara yang unik, seperti
dimana koefisiennya adalah skalar (yaitu, elemen F), yang disebut koordinat dari v di atas B. Namun, jika seseorang berbicara tentang himpunan koefisien, seseorang kehilangan korespondensi antara koefisien dan elemen basis, dan beberapa vektor mungkin memiliki himpunan koefisien yang sama. Sebagai contoh, dan memiliki koefisien yang sama {2, 3}, dan berbeda. Oleh karena itu, sering kali nyaman untuk bekerja dengan dasar yang teratur; ini biasanya dilakukan oleh pengindeksan elemen dasar oleh bilangan asli pertama. Kemudian, koordinat vektor membentuk urutan dengan indeks serupa, dan vektor sepenuhnya dicirikan oleh urutan koordinat. Basis terurut juga disebut frame, kata yang biasa digunakan, dalam berbagai konteks, untuk merujuk ke urutan data yang memungkinkan penentuan koordinat.
Misalkan, seperti biasa, menjadi himpunan n-tupel dari elemen F. Himpunan ini adalah F ruang vektor, dengan penjumlahan dan perkalian skalar ditentukan berdasarkan komponen. Peta
is a linear isomorphism from the vector space onto V. In other words, is the coordinate space of V, and the n-tuple is the coordinate vector of v.
Gambar invers oleh pada adalah n-tupel semua yang komponennya 0, kecuali yang ke i yaitu 1. membentuk dasar terurut dari yang disebut standar dasar atau dasar kanonik. Dasar yang diurutkan B adalah gambar oleh dari dasar kanonik .
Ini mengikuti dari apa yang mendahului setiap basis terurut adalah gambar dengan isomorfisme linier dari basis kanonik , dan bahwa setiap isomorfisme linier dari ke V dapat didefinisikan sebagai isomorfisme yang memetakan dasar kanonik ke urutan tertentu dasar dari V. Dengan kata lain, ini setara dengan mendefinisikan basis terurut dari V, atau isomorfisme linier dari ke V.
Perubahan basis
Maka V jadilah ruang vektor berdimensi n di atas bidang F. Diberikan dua pangkalan (order) dan dari V, sering kali berguna untuk menyatakan koordinat vektor x sehubungan dengan dalam hal koordinat sehubungan dengan Ini dapat dilakukan dengan rumus perubahan-basis , yang dijelaskan di bawah ini. Subskrip "lama" dan "baru" telah dipilih karena biasa digunakan untuk merujuk dan sebagai dasar lama dan dasar baru . Ini berguna untuk menggambarkan koordinat lama dengan yang baru, karena, secara umum, seseorang memiliki ekspresi yang melibatkan koordinat lama, dan jika seseorang ingin mendapatkan ekspresi yang setara dalam hal koordinat baru; ini diperoleh dengan mengganti koordinat lama dengan ekspresi mereka dalam bentuk koordinat baru.
Biasanya, vektor basis baru diberikan oleh koordinatnya di atas basis lama, yaitu
If and are the coordinates of a vector x over the old and the new basis respectively, the change-of-basis formula is
for i = 1, ..., n.
Rumus ini dapat ditulis secara ringkas dalam notasi matriks. Misalkan A adalah matriks dari dan
- dan
jadilah vektor kolom dari koordinat v di basis lama dan basis baru, maka rumus untuk mengubah koordinat adalah
Rumusnya dapat dibuktikan dengan mempertimbangkan dekomposisi vektor x pada dua basa: satu memiliki
dan
Rumus perubahan basis kemudian dari keunikan dekomposisi vektor atas basis, di sini adalah
untuk i = 1, ..., n.
Lihat pula
- Perubahan basis
- Bingkai ruang vektorLua error in Modul:WikidataDescription at line 7: bad argument #1 to 'sub' (string expected, got nil).
- Basis bolaLua error in Modul:WikidataDescription at line 7: bad argument #1 to 'sub' (string expected, got nil).
Catatan
- ^ Halmos, Paul Richard (1987) Finite-dimensional vector spaces (4th edition) Springer-Verlag, New York, page 10, ISBN 0-387-90093-4
Referensi
Referensi umum
- Blass, Andreas (1984), "Existence of bases implies the axiom of choice", Axiomatic set theory, Contemporary Mathematics volume 31, Providence, R.I.: American Mathematical Society, hlm. 31–33, ISBN 978-0-8218-5026-8, MR 0763890
- Brown, William A. (1991), Matrices and vector spaces, New York: M. Dekker, ISBN 978-0-8247-8419-5
- Lang, Serge (1987), Linear algebra, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96412-6
Referensi sejarah
- Banach, Stefan (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)" (PDF), Fundamenta Mathematicae (dalam bahasa Prancis), 3: 133–181, doi:10.4064/fm-3-1-133-181, ISSN 0016-2736
- Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) (dalam bahasa Jerman)
- Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics) (dalam bahasa Prancis), Paris: Hermann
- Dorier, Jean-Luc (1995), "A general outline of the genesis of vector space theory", Historia Mathematica, 22 (3): 227–261, doi:10.1006/hmat.1995.1024, MR 1347828
- Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (dalam bahasa Prancis), Chez Firmin Didot, père et fils
- Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (dalam bahasa Jerman), reprint: Hermann Grassmann. Translated by Lloyd C. Kannenberg. (2000), Extension Theory, Kannenberg, L.C., Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2031-5
- Hamilton, William Rowan (1853), Lectures on Quaternions, Royal Irish Academy
- Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) (dalam bahasa Jerman), diarsipkan dari versi asli tanggal 2009-04-12
- Moore, Gregory H. (1995), "The axiomatization of linear algebra: 1875–1940", Historia Mathematica, 22 (3): 262–303, doi:10.1006/hmat.1995.1025
- Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (dalam bahasa Italia), Turin

In mathematics, a set B of vectors in a vector space V is called a basis (Templat:Plural form: bases) if every element of V may be written in a unique way as a finite linear combination of elements of B. The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to B. The elements of a basis are called basis vectors.
Equivalently, a set B is a basis if its elements are linearly independent and every element of V is a linear combination of elements of B.[1] In other words, a basis is a linearly independent spanning set.
A vector space can have several bases; however all the bases have the same number of elements, called the dimension of the vector space.
This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces.
Definition
A basis B of a vector space V over a field F (such as the real numbers R or the complex numbers C) is a linearly independent subset of V that spans V. This means that a subset B of V is a basis if it satisfies the two following conditions:
- linear independence
- for every finite subset of B, if for some in F, then ;
- spanning property
- for every vector v in V, one can choose in F and in B such that .
The scalars are called the coordinates of the vector v with respect to the basis B, and by the first property they are uniquely determined.
A vector space that has a finite basis is called finite-dimensional. In this case, the finite subset can be taken as B itself to check for linear independence in the above definition.
It is often convenient or even necessary to have an ordering on the basis vectors, for example, when discussing orientation, or when one considers the scalar coefficients of a vector with respect to a basis without referring explicitly to the basis elements. In this case, the ordering is necessary for associating each coefficient to the corresponding basis element. This ordering can be done by numbering the basis elements. In order to emphasize that an order has been chosen, one speaks of an ordered basis, which is therefore not simply an unstructured set, but a sequence, an indexed family, or similar; see § Ordered bases and coordinates below.
Examples

The set R2 of the ordered pairs of real numbers is a vector space under the operations of component-wise addition
Properties
Many properties of finite bases result from the Steinitz exchange lemma, which states that, for any vector space V, given a finite spanning set S and a linearly independent set L of n elements of V, one may replace n well-chosen elements of S by the elements of L to get a spanning set containing L, having its other elements in S, and having the same number of elements as S.
Most properties resulting from the Steinitz exchange lemma remain true when there is no finite spanning set, but their proofs in the infinite case generally require the axiom of choice or a weaker form of it, such as the ultrafilter lemma.
If V is a vector space over a field F, then:
- If L is a linearly independent subset of a spanning set S ⊆ V, then there is a basis B such that
- V has a basis (this is the preceding property with L being the empty set, and S = V).
- All bases of V have the same cardinality, which is called the dimension of V. This is the dimension theorem.
- A generating set S is a basis of V if and only if it is minimal, that is, no proper subset of S is also a generating set of V.
- A linearly independent set L is a basis if and only if it is maximal, that is, it is not a proper subset of any linearly independent set.
If V is a vector space of dimension n, then:
- A subset of V with n elements is a basis if and only if it is linearly independent.
- A subset of V with n elements is a basis if and only if it is a spanning set of V.
Coordinates
Let V be a vector space of finite dimension n over a field F, and
Let, as usual, be the set of the n-tuples of elements of F. This set is an F-vector space, with addition and scalar multiplication defined component-wise. The map
The inverse image by of is the n-tuple all of whose components are 0, except the ith that is 1. The form an ordered basis of , which is called its standard basis or canonical basis. The ordered basis B is the image by of the canonical basis of .
It follows from what precedes that every ordered basis is the image by a linear isomorphism of the canonical basis of , and that every linear isomorphism from onto V may be defined as the isomorphism that maps the canonical basis of onto a given ordered basis of V. In other words, it is equivalent to define an ordered basis of V, or a linear isomorphism from onto V.
Change of basis
Let V be a vector space of dimension n over a field F. Given two (ordered) bases and of V, it is often useful to express the coordinates of a vector x with respect to in terms of the coordinates with respect to This can be done by the change-of-basis formula, that is described below. The subscripts "old" and "new" have been chosen because it is customary to refer to and as the old basis and the new basis, respectively. It is useful to describe the old coordinates in terms of the new ones, because, in general, one has expressions involving the old coordinates, and if one wants to obtain equivalent expressions in terms of the new coordinates; this is obtained by replacing the old coordinates by their expressions in terms of the new coordinates.
Typically, the new basis vectors are given by their coordinates over the old basis, that is,
This formula may be concisely written in matrix notation. Let A be the matrix of the , and
Related notions
Free module
If one replaces the field occurring in the definition of a vector space by a ring, one gets the definition of a module. For modules, linear independence and spanning sets are defined exactly as for vector spaces, although "generating set" is more commonly used than that of "spanning set".
Like for vector spaces, a basis of a module is a linearly independent subset that is also a generating set. A major difference with the theory of vector spaces is that not every module has a basis. A module that has a basis is called a free module. Free modules play a fundamental role in module theory, as they may be used for describing the structure of non-free modules through free resolutions.
A module over the integers is exactly the same thing as an abelian group. Thus a free module over the integers is also a free abelian group. Free abelian groups have specific properties that are not shared by modules over other rings. Specifically, every subgroup of a free abelian group is a free abelian group, and, if G is a subgroup of a finitely generated free abelian group H (that is an abelian group that has a finite basis), then there is a basis of H and an integer 0 ≤ k ≤ n such that is a basis of G, for some nonzero integers . For details, see Free abelian group § Subgroups.
Analysis
In the context of infinite-dimensional vector spaces over the real or complex numbers, the term Hamel basis (named after Georg Hamel[2]) or algebraic basis can be used to refer to a basis as defined in this article. This is to make a distinction with other notions of "basis" that exist when infinite-dimensional vector spaces are endowed with extra structure. The most important alternatives are orthogonal bases on Hilbert spaces, Schauder bases, and Markushevich bases on normed linear spaces. In the case of the real numbers R viewed as a vector space over the field Q of rational numbers, Hamel bases are uncountable, and have specifically the cardinality of the continuum, which is the cardinal number , where (aleph-nought) is the smallest infinite cardinal, the cardinal of the integers.
The common feature of the other notions is that they permit the taking of infinite linear combinations of the basis vectors in order to generate the space. This, of course, requires that infinite sums are meaningfully defined on these spaces, as is the case for topological vector spaces – a large class of vector spaces including e.g. Hilbert spaces, Banach spaces, or Fréchet spaces.
The preference of other types of bases for infinite-dimensional spaces is justified by the fact that the Hamel basis becomes "too big" in Banach spaces: If X is an infinite-dimensional normed vector space that is complete (i.e. X is a Banach space), then any Hamel basis of X is necessarily uncountable. This is a consequence of the Baire category theorem. The completeness as well as infinite dimension are crucial assumptions in the previous claim. Indeed, finite-dimensional spaces have by definition finite bases and there are infinite-dimensional (non-complete) normed spaces that have countable Hamel bases. Consider , the space of the sequences of real numbers that have only finitely many non-zero elements, with the norm . Its standard basis, consisting of the sequences having only one non-zero element, which is equal to 1, is a countable Hamel basis.
Example
In the study of Fourier series, one learns that the functions {1} ∪ { sin(nx), cos(nx) : n = 1, 2, 3, ... } are an "orthogonal basis" of the (real or complex) vector space of all (real or complex valued) functions on the interval [0, 2π] that are square-integrable on this interval, i.e., functions f satisfying
Geometry
The geometric notions of an affine space, projective space, convex set, and cone have related notions of basis.[4] An affine basis for an n-dimensional affine space is points in general linear position. A projective basis is points in general position, in a projective space of dimension n. A convex basis of a polytope is the set of the vertices of its convex hull. A cone basis[5] consists of one point by edge of a polygonal cone. See also a Hilbert basis (linear programming).
Random basis
For a probability distribution in Rn with a probability density function, such as the equidistribution in an n-dimensional ball with respect to Lebesgue measure, it can be shown that n randomly and independently chosen vectors will form a basis with probability one, which is due to the fact that n linearly dependent vectors x1, ..., xn in Rn should satisfy the equation det[x1 ⋯ xn] = 0 (zero determinant of the matrix with columns xi), and the set of zeros of a non-trivial polynomial has zero measure. This observation has led to techniques for approximating random bases.[6][7]

It is difficult to check numerically the linear dependence or exact orthogonality. Therefore, the notion of ε-orthogonality is used. For spaces with inner product, x is ε-orthogonal to y if (that is, cosine of the angle between x and y is less than ε).
In high dimensions, two independent random vectors are with high probability almost orthogonal, and the number of independent random vectors, which all are with given high probability pairwise almost orthogonal, grows exponentially with dimension. More precisely, consider equidistribution in n-dimensional ball. Choose N independent random vectors from a ball (they are independent and identically distributed). Let θ be a small positive number. Then for
|
(Eq. 1) |
N random vectors are all pairwise ε-orthogonal with probability 1 − θ.[7] This N growth exponentially with dimension n and for sufficiently big n. This property of random bases is a manifestation of the so-called measure concentration phenomenon.[8]
The figure (right) illustrates distribution of lengths N of pairwise almost orthogonal chains of vectors that are independently randomly sampled from the n-dimensional cube [−1, 1]n as a function of dimension, n. A point is first randomly selected in the cube. The second point is randomly chosen in the same cube. If the angle between the vectors was within π/2 ± 0.037π/2 then the vector was retained. At the next step a new vector is generated in the same hypercube, and its angles with the previously generated vectors are evaluated. If these angles are within π/2 ± 0.037π/2 then the vector is retained. The process is repeated until the chain of almost orthogonality breaks, and the number of such pairwise almost orthogonal vectors (length of the chain) is recorded. For each n, 20 pairwise almost orthogonal chains were constructed numerically for each dimension. Distribution of the length of these chains is presented.
Proof that every vector space has a basis
Let V be any vector space over some field F. Let X be the set of all linearly independent subsets of V.
The set X is nonempty since the empty set is an independent subset of V, and it is partially ordered by inclusion, which is denoted, as usual, by ⊆.
Let Y be a subset of X that is totally ordered by ⊆, and let LY be the union of all the elements of Y (which are themselves certain subsets of V).
Since (Y, ⊆) is totally ordered, every finite subset of LY is a subset of an element of Y, which is a linearly independent subset of V, and hence LY is linearly independent. Thus LY is an element of X. Therefore, LY is an upper bound for Y in (X, ⊆): it is an element of X, that contains every element of Y.
As X is nonempty, and every totally ordered subset of (X, ⊆) has an upper bound in X, Zorn's lemma asserts that X has a maximal element. In other words, there exists some element Lmax of X satisfying the condition that whenever Lmax ⊆ L for some element L of X, then L = Lmax.
It remains to prove that Lmax is a basis of V. Since Lmax belongs to X, we already know that Lmax is a linearly independent subset of V.
If there were some vector w of V that is not in the span of Lmax, then w would not be an element of Lmax either. Let Lw = Lmax ∪ {w}. This set is an element of X, that is, it is a linearly independent subset of V (because w is not in the span of Lmax, and Lmax is independent). As Lmax ⊆ Lw, and Lmax ≠ Lw (because Lw contains the vector w that is not contained in Lmax), this contradicts the maximality of Lmax. Thus this shows that Lmax spans V.
Hence Lmax is linearly independent and spans V. It is thus a basis of V, and this proves that every vector space has a basis.
This proof relies on Zorn's lemma, which is equivalent to the axiom of choice. Conversely, it has been proved that if every vector space has a basis, then the axiom of choice is true.[9] Thus the two assertions are equivalent.
See also
- Basis of a matroid
- Basis of a linear program
- Change of basisLua error in Modul:WikidataDescription at line 7: bad argument #1 to 'sub' (string expected, got nil).
- Frame of a vector spaceLua error in Modul:WikidataDescription at line 7: bad argument #1 to 'sub' (string expected, got nil).
- Spherical basisLua error in Modul:WikidataDescription at line 7: bad argument #1 to 'sub' (string expected, got nil).
Notes
- ^ Halmos, Paul Richard (1987). Finite-Dimensional Vector Spaces (edisi ke-4th). New York: Springer. hlm. 10. ISBN 978-0-387-90093-3.
- ^ Hamel 1905
- ^ Note that one cannot say "most" because the cardinalities of the two sets (functions that can and cannot be represented with a finite number of basis functions) are the same.
- ^ Rees, Elmer G. (2005). Notes on Geometry. Berlin: Springer. hlm. 7. ISBN 978-3-540-12053-7.
- ^ Kuczma, Marek (1970). "Some remarks about additive functions on cones". Aequationes Mathematicae. 4 (3): 303–306. doi:10.1007/BF01844160.
- ^ Igelnik, B.; Pao, Y.-H. (1995). "Stochastic choice of basis functions in adaptive function approximation and the functional-link net". IEEE Trans. Neural Netw. 6 (6): 1320–1329. doi:10.1109/72.471375. PMID 18263425.
- ^ a b c Gorban, Alexander N.; Tyukin, Ivan Y.; Prokhorov, Danil V.; Sofeikov, Konstantin I. (2016). "Approximation with Random Bases: Pro et Contra". Information Sciences. 364-365: 129–145. arXiv:1506.04631
 . doi:10.1016/j.ins.2015.09.021.
. doi:10.1016/j.ins.2015.09.021.
- ^ Artstein, Shiri (2002). "Proportional concentration phenomena of the sphere" (PDF). Israel Journal of Mathematics. 132 (1): 337–358. CiteSeerX 10.1.1.417.2375
 . doi:10.1007/BF02784520
. doi:10.1007/BF02784520  .
.
- ^ Blass 1984
References
General references
- Blass, Andreas (1984), "Existence of bases implies the axiom of choice" (PDF), Axiomatic set theory, Contemporary Mathematics volume 31, Providence, R.I.: American Mathematical Society, hlm. 31–33, ISBN 978-0-8218-5026-8, MR 0763890
- Brown, William A. (1991), Matrices and vector spaces, New York: M. Dekker, ISBN 978-0-8247-8419-5
- Lang, Serge (1987), Linear algebra, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96412-6
Historical references
- Banach, Stefan (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)" (PDF), Fundamenta Mathematicae (dalam bahasa Prancis), 3: 133–181, doi:10.4064/fm-3-1-133-181, ISSN 0016-2736
- Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) (dalam bahasa Jerman)
- Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics) (dalam bahasa Prancis), Paris: Hermann
- Dorier, Jean-Luc (1995), "A general outline of the genesis of vector space theory", Historia Mathematica, 22 (3): 227–261, doi:10.1006/hmat.1995.1024
 , MR 1347828
, MR 1347828 - Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (dalam bahasa Prancis), Chez Firmin Didot, père et fils
- Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (dalam bahasa Jerman), reprint: Hermann Grassmann. Translated by Lloyd C. Kannenberg. (2000), Extension Theory, Kannenberg, L.C., Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2031-5
- Hamel, Georg (1905), "Eine Basis aller Zahlen und die unstetigen Lösungen der Funktionalgleichung f(x+y)=f(x)+f(y)", Mathematische Annalen (dalam bahasa Jerman), Leipzig, 60 (3): 459–462, doi:10.1007/BF01457624
- Hamilton, William Rowan (1853), Lectures on Quaternions, Royal Irish Academy
- Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) (dalam bahasa Jerman), diarsipkan dari versi asli tanggal 2009-04-12
- Moore, Gregory H. (1995), "The axiomatization of linear algebra: 1875–1940", Historia Mathematica, 22 (3): 262–303, doi:10.1006/hmat.1995.1025

- Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (dalam bahasa Italia), Turin
External links
- Instructional videos from Khan Academy
- "Linear combinations, span, and basis vectors". Essence of linear algebra. August 6, 2016. Diarsipkan dari versi asli tanggal 2021-11-17 – via YouTube.
- Hazewinkel, Michiel, ed. (2001) [1994], "Basis", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4



























































































