Himpunan terurut parsial
| Relasi biner | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Simbol "✓" menunjukkan bahwa sifat kolom diperlukan dalam definisi baris. Misalnya, definisi relasi ekuivalen diperlukan menjadi simetris. Semua definisi secara diam-diam memerlukan ketransitifan dan refleksivitas. |

Dalam matematika, terutama teori urutan, himpunan terurut parsial (bahasa Inggris: partially ordered set) atau poset memformalkan dan memperumum konsep intuitif dari suatu urutan, pengurutan, atau susunan elemen-elemen dari sebuah himpunan. Poset terdiri dari sebuah himpunan bersama dengan relasi biner yang menunjukkan, untuk pasangan elemen-elemen tertentu dalam himpunan, salah satu elemen mendahului elemen yang lain dalam urutan. Relasi itu sendiri disebut "urutan parsial". Kata parsial digunakan untuk menandakan bahwa semua pasangan elemen tidak perlu dibandingkan. Artinya, mungkin saja ada pasangan elemen yang tidak mendahului satu sama yang lain di dalam poset. Urutan parsial memperumum konsep urutan total, yakni urutan di mana setiap pasangan dapat dibandingkan.
Satu contoh familiar dari himpunan yang tersusun sebagian adalah sekumpulan orang yang diurutkan berdasarkan silsilah keturunan. Beberapa pasang orang memiliki relasi keturunan, tetapi pasangan orang lainnya (misal, sesama saudara kandung) tidak dapat dibandingkan, karena tidak ada yang menjadi keturunan dari yang lain.
Definisi
[sunting | sunting sumber]Urutan parsial mendefinisikan konsep perbandingan. Dua elemen dan dapat berada di salah satu dari empat hubungan yang disjoin satu sama lainnya: antara atau dan tidak dapat dibandingkan.[1][2]
Sebuah himpunan yang dilengkapi urutan parsial disebut himpunan terurut parsial (juga disebut poset). Istilah "himpunan terurut" terkadang digunakan, selama konteks urutan yang dimaksud jelas. Alasannya, himpunan terurut total juga dapat disebut "himpunan terurut", khususnya di bidang matematika yang lebih lazim menemui struktur tersebut ketimbang poset. Relasi urutan pada sebuah poset dapat divisualisasikan lewat diagram Hasse poset tersebut.[3]
Secara formal, relasi urutan parsial adalah sebuah relasi homogen yang bersifat transitif dan antisimetris.[4] Ada dua subdefinisi umum untuk relasi urutan parsial, yakni relasi urutan parsial yang reflektif dan yang tak-reflektif, yang masing-masing disebut dengan "tak-tegas" dan "tegas". Kedua definisi ini dapat digabungkan dalam korespodensi satu-satu; sehingga setiap urutan parsial tegas berhubungan dengan tepat satu urutan parsial tak-tegas, dan sebaliknya. Istilah urutan parsial umumnya mengacu pada versi tak-tegas dari relasi urutan.
Urutan parsial tak-tegas
[sunting | sunting sumber]Urutan parsial reflektif, lemah,[4] atau tak-tegas,[5] adalah relasi homogen ≤ pada sebuah himpunan yang bersifat reflektif, antisimetris, dan transitif. Dengan kata lain, untuk setiap akan berlaku:
- Relasi reflektif: , maksudnya, setiap elemen berelasi dengan dirinya sendiri.
- Relasi antisimetri: jika dan maka , mengartikan tidak ada dua elemen berbeda yang saling mendahului.
- Relasi transitif: jika dan maka .
Urutan parsial tak-tegas juga dikenal sebagai pratatanan antisimetris.
Urutan parsial tegas
[sunting | sunting sumber]Urutan parsial irreflektif, kuat,[4] atau tegas, adalah relasi homogen < pada sebuah himpunan yang bersifat reflektif, antisimetris, dan transitif. Dengan kata lain, urutan ini memenuhi sifat-sifat berikut, untuk semua
- Relasi irreflektif: Tidak , maksudnya, tidak ada elemen yang berelasi dengan dirinya sendiri (relasi ini juga disebut anti-reflektif).
- Relasi antisimetri: Jika maka tidak .
- Relasi transitif: Jika dan maka .
Sifat irreflektif dan transitif bersamaan mengimplikasikan sifat asimetri. Selain itu, sifat asimetri juga menyebabkan sifat irreflektif. Dengan kata lain, relasi yang transitif bersifat asimetri jika dan hanya jika juga bersifat irreflektif.[6] Hal ini mengakibatkan definisi diatas tidak berubah bahkan jika relasi irreflektif atau asimetri (namun tidak keduanya) tidak disertakan. Urutan parsial tegas juga dikenal sebagai pratatanan tegas.
Korespodensi relasi tegas dan tak-tegas
[sunting | sunting sumber]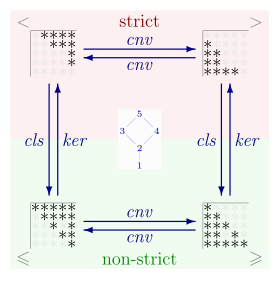
Urutan parsial tegas dan tak-tegas pada himpunan memiliki hubungan yang erat. Urutan parsial tak-tegas dapat diubah menjadi urutan parsial tegas dengan menghilangkan semua hubungan yang memiliki bentuk artinya, himpunan parsial tegas adalah himpunan dengan adalah relasi identitas pada dan menyatakan operasi pengurangan pada himpunan. Urutan parsial tegas pada dapat diubah menjadi urutan parsial tak-tegas dengan menggabungkannya dengan realsi identitas; yakni . Akibatnya, jika adalah urutan parsial tak-tegas, maka urutan parsial tegas yang berkorespodensi dengannya adalah irreflexive kernel:Sebalinya, jika < adalah urutan parsial tegas, maka urutan parsial tak-tegas yang berkorespodensi dengannya reflexive closure:
Notasi
[sunting | sunting sumber]Poset dapat disajikan sebagai rangkap-3 ,[7] dengan adalah relasi parsial tak-tegas pada , adalah relasi parsial tegas yang berkorespodensi pada (irreflexive kernel dari ). Simbol digunakan untuk menunjukkan dual dari , dan untuk menunjukkan dual dari .
Salah satu dari empat relasi parsial pada suatu himpunan akan secara unik menentukan tiga relasi yang lain. Akibatnya, bentuk atau dapat digunakan sebagai notasi, dan berasumsi bahwa relasi-relasi yang lain akan didefinisikan secara wajar. Pendefinisian menggunakan urutan parsial tak-tegas adalah yang paling umum. Beberapa penulis menggunakan simbol selain , seperti [8] dan ,[9] untuk membedakannya dengan urutan total.
Ketika mengacu pada urutan parsial, sebaiknya tidak dianggap sebagai komplemen dari . Relasi adalah konvers irreflexive kernel dari , yang akan selalu berupa subset komplemen dari , namun sama dengan komplemen dari jika, dan hanya jika, adalah urutan total.[a]
Contoh
[sunting | sunting sumber]Urutan pada produk Kartesius dari himpunan urutan sebagian
[sunting | sunting sumber]

Untuk meningkatkan kekuatan, yaitu, penurunan set pasangan, tiga dari kemungkinan pesanan parsial pada Produk Kartesius dari dua set yang dipesan sebagian adalah (lihat gambar):
- urutan leksikografis: (a,b) ≤ (c,d) jika a < c atau (a = c dan b ≤ d);
- urutan produk: (a,b) ≤ (c,d) jika a ≤ c dan b ≤ d;
- penutupan refleksif dari produk langsung dari pesanan ketat yang sesuai: (a,b) ≤ (c,d) jika (a < c dan b < d) atau (a = c dan b = d).
Ketiganya dapat didefinisikan secara serupa untuk produk Kartesius lebih dari dua himpunan.
Diterapkan ke ruang vektor terurut di atas bidang yang sama, hasilnya dalam setiap kasus juga merupakan ruang vektor terurut.
Lihat pula urutan pada produk Kartesius dari himpunan berurutan total.
Jumlah himpunan yang diurutkan sebagian
[sunting | sunting sumber]
Cara lain untuk menggabungkan dua poset adalah jumlah ordinal[10] (or jumlah linear[11]), Z = X ⊕ Y, ditentukan pada penyatuan himpunan yang mendasari X dan Y berdasarkan urutan a ≤Z b jika dan hanya jika:
- a, b ∈ X dengan a ≤X b, atau
- a, b ∈ Y dengan a ≤Y b, atau
- a ∈ X dan b ∈ Y.
Jika dua poset urutan rapi, maka jumlah ordinalnya juga.[12] Operasi penjumlahan ordinal adalah salah satu dari dua operasi yang digunakan untuk membentuk urutan parsial deret-paralel, dan dalam konteks ini disebut komposisi seri. Operasi lain yang digunakan untuk membentuk tatanan ini, penyatuan dua himpunan yang terurut sebagian (tanpa hubungan keteraturan antara unsur satu himpunan dan unsur himpunan lainnya) disebut dalam komposisi paralel konteks ini.
Pemetaan antar poset
[sunting | sunting sumber]
Diberikan dua set yang dipesan sebagian (S, ≤) dan (T, ≤), sebuah fungsi f: S → T disebut pengawetan urutan, atau monoton, atau isoton, jika untuk x dan y pada S , x ≤ y menyiratkan f(x) ≤ f(y).
Jika (U, ≤) juga merupakan himpunan yang dipesan sebagian, dan keduanya f: S → T dan g: T → U menjaga keteraturan, komposisi mereka g∘f : S → U juga menjaga ketertiban. Sebuah fungsi f: S → T disebut urutan refleksi jika untuk x dan y pada S , f(x) ≤ f(y) menyiratkan x ≤ y. Jika f baik untuk menjaga ketertiban maupun mencerminkan ketertiban, maka ini disebut urutan pembenaman dari (S, ≤) menjadi (T, ≼). Dalam kasus terakhir, f harus injektif, karena f(x) = f(y) menyiratkan x ≤ y dan y ≤ x. Jika ada urutan pembenaman antara dua himpunan terurut parsial S dan T, satunya dikatakan bahwa S dapat menjadi terbenam ke dalam T . Jika urutan pembenaman f: S → T adalah bijektif, ini disebut 'isomorfisme tatanan' , dan urutan parsial (S,≤) dan (T ,≤) dikatakan menjadi isomorfik. Ordo isomorfik memiliki struktur serupa diagram Hasse (lih. Gambar kanan). Dapat ditunjukkan bahwa jika peta pelestarian pesanan f: S → T dan g: T → S dirumuskan g∘f dan f∘g menghasilkan fungsi identitas pada S dan T , lalu S dan T adalah urutan-isomorfik.

Misalnya, pemetaan f: ℕ → ℙ(ℕ) dari himpunan bilangan asli (diurutkan berdasarkan pembagian) ke himpunan daya dari bilangan asli (diurutkan berdasarkan set inklusi) dapat ditentukan dengan mengambil setiap bilangan ke himpunan pembagi utama. Ini menjaga keteraturan: jika x membagi y , maka setiap pembagi utama dari x juga merupakan pembagi utama dari y . Namun, ini bukan injektif (karena memetakan 12 dan 6 ke {2, 3}) atau mencerminkan urutan (karena 12 tidak membagi 6). Mengambil alih-alih setiap bilangan ke himpunan pangkat utama -nya mendefinisikan peta g: ℕ → ℙ(ℕ) yaitu memelihara ketertiban, mencerminkan ketertiban, dan karenanya merupakan penyematan pesanan. Ini bukan isomorfisme urutan (karena misalnya tidak memetakan nomor apa pun ke himpunan {4}), tapi bisa dibuat dengan membatasi kodomain menjadi g(ℕ). Gambar kanan menunjukkan subhimpunan dari ℕ dan gambar isomorfiknya di bawah g . Konstruksi isomorfisme-tatanan semacam itu ke dalam himpunan daya dapat digeneralisasikan ke kelas luas tatanan parsial, disebut kekisi distributif, lihat "Teorema wakilan Birkhoff".
Konsep yang berkaitan
[sunting | sunting sumber]Ekstrema
[sunting | sunting sumber]
Ada beberapa pengertian tentang elemen "terbesar" dan "terkecil" dalam sebuah poset P , terutama:
- Elemen terbesar dan elemen terkecil: Sebuah elemen g dalam P adalah elemen terbesar jika untuk setiap elemen a dalam P , a ≤ g. Sebuah elemen m dalam P adalah elemen terkecil jika untuk setiap elemen a dalam P , a ≥ m . Poset hanya dapat memiliki satu elemen terbesar atau terkecil.
- Elemen maksimal dan elemen minimal: Elemen g di P adalah elemen maksimal jika tidak ada elemen a di P sehingga a > g . Demikian pula, elemen m di P adalah elemen minimal jika tidak ada elemen a di P sehingga a < m . Jika poset memiliki elemen terbesar, itu harus menjadi elemen maksimal yang unik, tetapi jika tidak, bisa ada lebih dari satu elemen maksimal, dan juga untuk elemen terkecil dan elemen minimal.
- Batas atas dan bawah: Untuk subset A dari P , elemen x dalam P adalah batas atas dari A if a ≤ x, untuk setiap elemen a pada A. Secara khusus, x tidak perlu berada di A untuk menjadi batas atas dari A . Demikian pula, elemen x dalam P adalah batas bawah dari A jika a ≥ x, untuk setiap elemen a di A . Unsur terbesar dari P adalah batas atas P , dan unsur terkecil adalah batas bawah P .

Misalnya, perhatikan bilangan bulat positif, yang diurutkan berdasarkan dapat dibagi: 1 adalah elemen terkecil, karena membagi semua elemen lainnya; di sisi lain poset ini tidak memiliki elemen terbesar (meskipun jika seseorang akan menyertakan 0 dalam poset, yang merupakan kelipatan dari bilangan bulat, itu akan menjadi elemen terbesar; lihat gambar). Kumpulan yang diurutkan sebagian ini bahkan tidak memiliki elemen maksimal, karena ada g yang terbagi misalnya 2g, yang berbeda dari itu, lagu tidak maksimal. Jika angka 1 dikecualikan, sambil menjaga agar dapat dibagi sebagai urutan pada elemen yang lebih besar dari 1, maka poset yang dihasilkan tidak memiliki elemen terkecil, tetapi bilangan prima adalah elemen minimal untuk itu. Dalam poset ini, 60 adalah batas atas (meskipun bukan batas atas terkecil) dari subset {2, 3, 5, 10}, yang tidak memiliki batas bawah (karena 1 tidak ada di poset); di sisi lain 2 adalah batas bawah dari himpunan bagian dari pangkat 2, yang tidak memiliki batas atas.
Banyaknya urutan parsial
[sunting | sunting sumber]Urutan A001035 di OEIS memberikan jumlah urutan parsial pada satu himpunan unsur dinamakan n :
| Elemen | Any | Transitif | Refleksif | Urutan utama | Urutan sebagian | Total praorder | Total urutan | Relasi kesetaraan |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 16 | 13 | 4 | 4 | 3 | 3 | 2 | 2 |
| 3 | 512 | 171 | 64 | 29 | 19 | 13 | 6 | 5 |
| 4 | 65,536 | 3,994 | 4,096 | 355 | 219 | 75 | 24 | 15 |
| n | 2n2 | 2n2−n | ∑n k=0 k! S(n, k) |
n! | ∑n k=0 S(n, k) | |||
| OEIS | A002416 | A006905 | A053763 | A000798 | A001035 | A000670 | A000142 | A000110 |
Jumlah urutan parsial ketat sama dengan jumlah pesanan parsial.
Jika hitungan dilakukan hanya hingga isomorfisme, urutan 1, 1, 2, 5, 16, 63, 318,… (barisan A000112 pada OEIS) diperoleh.
Ekstensi linear
[sunting | sunting sumber]
Urutan parsial ≤* pada himpunan X adalah ekstensi dari urutan parsial lain ≤ on X asalkan untuk semua elemen x dan y dari X , setiap kali x ≤ y , hal itu juga terjadi x ≤* y. A ekstensi linier adalah ekstensi yang juga merupakan tatanan linear (yaitu total). Setiap pesanan parsial dapat diperpanjang menjadi pesanan total (prinsip perpanjangan urutan).[14]
Dalam ilmu komputer, Algoritma untuk menemukan ekstensi linier dari urutan parsial (diwakilkan sebagai jangkauan urutan grafik asiklik terarah) disebut penyortiran topologis.
Dalam teori kategori
[sunting | sunting sumber]Setiap poset (dan setiap set praorder) dapat dianggap sebagai kategori di mana, untuk objek x dan y , paling banyak ada satu morfisme dari x hingga y . Lebih eksplisit lagi, maka hom(x, y) = {(x, y)} if x ≤ y (dan sebalik himpunan kosong) dan (y, z)∘(x, y) = (x, z). Kategori seperti itu kadang disebut posetal .
Poset adalah ekuivalen satu sama lain jika dan hanya jika poset tersebut isomorfik. Dalam poset, elemen terkecil, jika ada, adalah objek awal, dan elemen terbesar, jika ada, adalah objek terminal. Selain itu, setiap set yang dipesan sebelumnya setara dengan poset. Akhirnya, setiap subkategori poset adalah isomorfisme tertutup.
Urutan parsial dalam ruang topologi
[sunting | sunting sumber]Jika P adalah himpunan terurut parsial yang juga telah diberi struktur ruang topologi, maka biasanya diasumsikan bahwa adalah subhimpunantertutup dari topologi ruang produk . Di bawah asumsi ini, hubungan urutan parsial berperilaku baik pada batas dalam arti jika , dan , dan untuk , , kemudian .[15]
Lihat pula
[sunting | sunting sumber]- Antimatroid, formalisasi urutan pada satu set yang memungkinkan kelompok urutan yang lebih umum daripada poset
- Himpunan kausal, pendekatan berbasis poset untuk gravitasi kuantum
- Grafik komparabilitas
- Urutan kompleks
- Himpunan terarah
- Poset dinilai
- Aljabar insiden
- kisi
- Poset hingga secara lokal
- Fungsi Mbius pada posets
- Himpunan nested
- Politico urutan
- Grup urutan
- Topologi poset, sejenis ruang topologi yang dapat didefinisikan dari poset manapun
- Kontinuitas Scott - kontinuitas fungsi antara dua orde parsial.
- Semikisi
- Semiorder
- Dominasi stokastik
- Pengurutan lemah – urutan parsial ketat "<" di mana relasi "neither a < b nor b < a" bersifat transitif.
- Total urutan
- Pohon (struktur data set inclusion)
- Lemma Zorn
Catatan
[sunting | sunting sumber]- ^ "Finite posets". Sage 9.2.beta2 Reference Manual: Combinatorics. Diakses tanggal 5 January 2022.
compare_elements(x, y): Compare x and y in the poset. If x<y, return -1. If x=y, return 0. If x>y, return 1. If x and y are not comparable, return None.
- ^ Chen, Peter; Ding, Guoli; Seiden, Steve. "On Poset Merging" (PDF): 2. Diakses tanggal 5 January 2022.
A comparison between two elements s, t in S returns one of three distinct values, namely s≤t, s>t or s|t.
- ^ Merrifield, Richard E.; Simmons, Howard E. (1989). Topological Methods in Chemistry
 . New York: John Wiley & Sons. hlm. 28. ISBN 0-471-83817-9. Diakses tanggal 27 July 2012.
. New York: John Wiley & Sons. hlm. 28. ISBN 0-471-83817-9. Diakses tanggal 27 July 2012. A partially ordered set is conveniently represented by a Hasse diagram...
- ^ a b c Wallis, W. D. (14 March 2013). A Beginner's Guide to Discrete Mathematics (dalam bahasa Inggris). Springer Science & Business Media. hlm. 100. ISBN 978-1-4757-3826-1.
- ^ Simovici, Dan A.; Djeraba, Chabane (2008). "Partially Ordered Sets". Mathematical Tools for Data Mining: Set Theory, Partial Orders, Combinatorics. Springer. ISBN 9781848002012.
- ^ Flaška, V.; Ježek, J.; Kepka, T.; Kortelainen, J. (2007). "Transitive Closures of Binary Relations I". Acta Universitatis Carolinae. Mathematica et Physica. Prague: School of Mathematics - Physics Charles University. 48 (1): 55–69. Lemma 1.1 (iv). This source refers to asymmetric relations as "strictly antisymmetric".
- ^ Avigad, Jeremy; Lewis, Robert Y.; van Doorn, Floris (29 March 2021). "13.2. More on Orderings". Logic and Proof (edisi ke-Release 3.18.4). Diakses tanggal 24 July 2021.
So we can think of every partial order as really being a pair, consisting of a weak partial order and an associated strict one.
- ^ Rounds, William C. (7 March 2002). "Lectures slides" (PDF). EECS 203: DISCRETE MATHEMATICS. Diakses tanggal 23 July 2021.
- ^ Kwong, Harris (25 April 2018). "7.4: Partial and Total Ordering". A Spiral Workbook for Discrete Mathematics (dalam bahasa Inggris). Diakses tanggal 23 July 2021.
- ^ Neggers, J.; Kim, Hee Sik (1998), "4.2 Product Order and Lexicographic Order", Basic Posets, World Scientific, hlm. 62–63, ISBN 9789810235895
- ^ Davey, B. A.; Priestley, H. A. (2002). Introduction to Lattices and Order (edisi ke-Second). New York: Cambridge University Press. hlm. 17–18. ISBN 0-521-78451-4 – via Google Books.
- ^ P. R. Halmos (1974). Naive Set Theory
 . Springer. hlm. 82. ISBN 978-1-4757-1645-0.
. Springer. hlm. 82. ISBN 978-1-4757-1645-0.
- ^ Davey, B. A.; Priestley, H. A. (2002). "Maps between ordered sets". Introduction to Lattices and Order (edisi ke-2nd). New York: Cambridge University Press. hlm. 23–24. ISBN 0-521-78451-4. MR 1902334..
- ^ Jech, Thomas (2008) [1973]. The Axiom of Choice. Dover Publications. ISBN 978-0-486-46624-8.
- ^ Ward, L. E. Jr (1954). "Partially Ordered Topological Spaces". Proceedings of the American Mathematical Society. 5 (1): 144–161. doi:10.1090/S0002-9939-1954-0063016-5
 . hdl:10338.dmlcz/101379.
. hdl:10338.dmlcz/101379.
Referensi
[sunting | sunting sumber]- Deshpande, Jayant V. (1968). "On Continuity of a Partial Order". Proceedings of the American Mathematical Society. 19 (2): 383–386. doi:10.1090/S0002-9939-1968-0236071-7
 .
. - Schmidt, Gunther (2010). Relational Mathematics. Encyclopedia of Mathematics and its Applications. 132. Cambridge University Press. ISBN 978-0-521-76268-7.
- Bernd Schröder (11 May 2016). Ordered Sets: An Introduction with Connections from Combinatorics to Topology. Birkhäuser. ISBN 978-3-319-29788-0.
- Stanley, Richard P. (1997). Enumerative Combinatorics 1. Cambridge Studies in Advanced Mathematics. 49. Cambridge University Press. ISBN 0-521-66351-2.
Pranala luar
[sunting | sunting sumber]
Kesalahan pengutipan: Ditemukan tag <ref> untuk kelompok bernama "lower-alpha", tapi tidak ditemukan tag <references group="lower-alpha"/> yang berkaitan
















































