Segitiga sama kaki: Perbedaan antara revisi
Dedhert.Jr (bicara | kontrib) →Panjang garis bagi sudut: matematikawan Tag: Suntingan visualeditor-wikitext |
Dedhert.Jr (bicara | kontrib) Tag: Suntingan visualeditor-wikitext |
||
| (43 revisi perantara oleh 6 pengguna tidak ditampilkan) | |||
| Baris 1: | Baris 1: | ||
{{pp}} |
|||
{{Artikel bagus}} |
|||
{{Infobox polygon |
{{Infobox polygon |
||
|name=Segitiga sama kaki |
|name=Segitiga sama kaki |
||
| Baris 15: | Baris 17: | ||
}} |
}} |
||
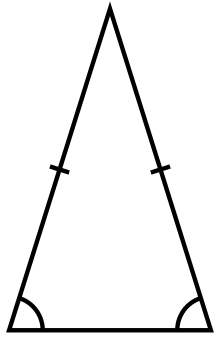
Dalam [[geometri]], '''segitiga sama kaki''' ({{Lang-en|isosceles triangle}}) adalah segitiga yang memiliki dua sisi yang sama panjangnya. Segitiga ini terkadang dinyatakan memiliki ''tepat'' dua sisi yang sama panjang. Segitiga ini juga terkadang dinyatakan ''setidaknya'' mempunyai dua sisi yang sama panjang, dan pernyataan ini meliputi [[segitiga sama sisi]] sebagai kasus istimewa. Contoh-contoh segitiga sama kaki di antaranya [[segitiga siku-siku sama kaki]], [[Segitiga emas (matematika)|segitiga emas]], muka [[Bipiramida (geometri)|bipiramida]] |
Dalam [[geometri]], '''segitiga sama kaki''' ({{Lang-en|isosceles triangle}}) adalah [[segitiga]] yang memiliki dua sisi yang sama panjangnya. Segitiga ini terkadang dinyatakan memiliki ''tepat'' dua sisi yang sama panjang. Segitiga ini juga terkadang dinyatakan ''setidaknya'' mempunyai dua sisi yang sama panjang, dan pernyataan ini meliputi [[segitiga sama sisi]] sebagai kasus istimewa. Contoh-contoh segitiga sama kaki di antaranya [[segitiga siku-siku sama kaki]], [[Segitiga emas (matematika)|segitiga emas]], serta [[Muka (geometri)|muka]] yang terdapat di [[Bipiramida (geometri)|bipiramida]] dan [[bangun ruang Catalan]]. |
||
Kajian matematika tentang segitiga sama kaki berawal dari [[matematika Mesir kuno]] dan [[matematika Babilonia]]. Segitiga sama kaki bahkan dipakai sebagai hiasan pada masa sebelumnya. Segitiga ini sering ditemukan dalam arsitektur dan desain, seperti [[pedimen]] dan [[atap pelana]] bangunan. |
Kajian matematika tentang segitiga sama kaki berawal dari [[matematika Mesir kuno]] dan [[matematika Babilonia]]. Segitiga sama kaki bahkan dipakai sebagai hiasan pada masa sebelumnya. Segitiga ini sering ditemukan dalam arsitektur dan desain, seperti [[pedimen]] dan [[atap pelana]] bangunan. |
||
Segitiga sama kaki mempunyai dua sisi yang sama panjang yang disebut kaki, sementara sisi ketiganya disebut alas segitiga. Dimensi segitiga lain seperti tinggi, luas, dan keliling, dapat dihitung dengan rumus sederhana menggunakan panjang kaki dan alas segitiga. Setiap segitiga sama kaki memiliki sumbu simetri di sepanjang [[Garis bagi#Garis bagi ruas garis yang tegak lurus|garis bagi yang tegak lurus]] dari alasnya. Dua sudut yang berhadapan dengan kaki segitiga adalah sama dan selalu [[Sudut lancip|lancip]], sehingga penggolongan segitiga berupa segitiga lancip, siku-siku, atau tumpul, hanya bergantung pada sudut yang diapit oleh dua kaki segitiga. |
|||
==Penggolongan dan sudut segitiga== |
==Penggolongan dan sudut segitiga== |
||
[[Euklides]] mendefinisikan segitiga sama kaki sebagai segitiga yang tepat memiliki dua sisi yang sama panjang,{{ |
[[Euklides]] mendefinisikan segitiga sama kaki sebagai segitiga yang tepat memiliki dua sisi yang sama panjang,{{sfn|Heath|1956|loc=hlm. 187, Definisi 20}} sedangkan penjelasan modern lebih mendefinisikan segitiga sama kaki sebagai segitiga yang setidaknya memiliki dua sisi yang sama panjang. Perbedaan dari kedua definisi tersebut adalah bahwa definisi dari versi modern meliputi segitiga sama sisi (dengan panjang dari ketiga sisinya sama) sebagai kasus istimewa dari segitiga sama kaki.{{sfn|Stahl|2003|loc=[https://books.google.de/books?id=jLk7lu3bA1wC&pg=PA37 hlm. 37]}} Segitiga yang bukan sama kaki (dengan panjang dari ketiga sisinya tidak sama) disebut [[segitiga sembarang]].{{sfn|Usiskin|Griffin|2008|page=4}} |
||
Dalam segitiga sama kaki yang memiliki tepat dua sisi yang sama, sisi yang sama disebut [[Kaki (geometri)|kaki]] dan sisi ketiga disebut [[Alas (geometri)|alas]]. Sudut yang diapit oleh kedua sisi disebut |
Dalam segitiga sama kaki yang memiliki tepat dua sisi yang sama, sisi yang sama disebut [[Kaki (geometri)|kaki]] dan sisi ketiga disebut [[Alas (geometri)|alas]]. Sudut yang diapit oleh kedua sisi disebut sudut puncak (''vertex angle''), sedangkan sudut yang diapit oleh alas segitiga dan salah satu sisi lainnya disebut sudut alas (''base angle'').{{sfn|Jacobs|1974|page=144}} Titik yang berhadapan dengan alas segitiga disebut [[Titik puncak (geometri)|titik puncak segitiga]].{{sfn|Gottschau|Haverkort|Matzke|2018}} Dalam kasus segitiga sama sisi, karena semua sisi segitiga adalah sama, maka sebarang sisi dapat dikatakan sebagai alas.{{sfn|Lardner|1840|page=46}} |
||
{{multiple image |
{{multiple image |
||
| Baris 40: | Baris 42: | ||
}} |
}} |
||
Penggolongan segitiga sama kaki dapat menjadi [[Segitiga lancip dan tumpul|lancip, siku-siku, ataupun tumpul]] hanya tergantung sudut puncaknya. Dalam [[geometri Euklides]], sudut alas segitiga tidak tumpul (lebih besar dari 90°) atau siku-siku (sama dengan 90°) karena sudutnya sama dengan jumlah sudut dalam dari sebarang segitiga, yaitu 180°.{{sfn|Lardner|1840|page=46}} Karena segitiga merupakan segitiga tumpul atau siku-siku jika dan hanya jika salah satu sudutnya tumpul atau siku-siku, maka segitiga sama kaki dapat berupa segitiga tumpul, siku-siku, atau lancip jika dan hanya jika sudut puncaknya adalah tumpul, siku-siku, atau lancip.{{sfn|Gottschau|Haverkort|Matzke|2018}} Penggolongan segitiga sama kaki dan bangun datar umumnya dipakai [[Edwin Abbott Abbott|Edwin Abbott]] dalam novel ''[[Flatland]]'' sebagai sindiran tentang [[Stratifikasi sosial|hierarki sosial]], contohnya segitiga sama kaki yang menyatakan [[buruh|kelas pekerja]], dengan segitiga lancip sama kaki menyatakan tingkat yang lebih tinggi daripada segitiga sama kaki siku-siku ataupun tumpul.{{sfn|Barnes|2012}} |
|||
{{multiple image |
{{multiple image |
||
| total_width = 600 |
| total_width = 600 |
||
| header = |
| header = Bangun ruang Catalan dengan muka segitiga sama kaki |
||
| image1 = Triakistetrahedron.jpg |
| image1 = Triakistetrahedron.jpg |
||
| caption1 = [[Tetrahedron triakis]] |
| caption1 = [[Tetrahedron triakis]] |
||
| Baris 57: | Baris 59: | ||
}} |
}} |
||
Selain [[segitiga siku-siku sama kaki]], ada beberapa bangun segitiga sama kaki spesifik lainnya juga dikaji. Segitiga tersebut di antaranya [[segitiga Calabi]] (segitiga yang memiliki tiga persegi dalam yang kongruen),{{ |
Selain [[segitiga siku-siku sama kaki]], ada beberapa bangun segitiga sama kaki spesifik lainnya juga dikaji. Segitiga tersebut di antaranya [[segitiga Calabi]] (segitiga yang memiliki tiga persegi dalam yang kongruen),{{sfn|Conway|Guy|1996}} [[Segitiga emas (matematika)|segitiga emas]] dan [[gnomon emas]] (dua segitiga sama kaki yang perbandingan antara panjang sisi dengan alasnya bernilai [[rasio emas]]),{{sfn|Loeb|1992}} segitiga dengan sudut 80-80-20 ditemukan dalam teka-teki [[Langley's Adventitious Angles]],{{sfn|Langley|1922}} dan segitiga dengan sudut 30-30-120 ditemukan dalam [[pengubinan segitiga triakis]]. Masing-masing kelima [[bangun ruang Catalan]], yaitu [[tetrahedron triakis]], [[oktahedron triakis]], [[heksahedron triakis]], [[dodekahedron pentakis]], dan [[ikosahedron triakis]], mempunyai muka berbentuk segitiga sama kaki; sama halnya dengan tak berhingga banyaknya [[limas]]{{sfn|Lardner|1840|page=46}} dan [[Bipiramida (geometri)|bipiramida]].{{sfn|Montroll|2009}} |
||
==Rumus== |
==Rumus== |
||
===Garis tinggi segitiga sama kaki=== |
===Garis tinggi segitiga sama kaki=== |
||
Untuk sebarang segitiga sama kaki, keenam [[ruas garis]] berikut |
Untuk sebarang segitiga sama kaki, keenam [[ruas garis]] berikut berimpitan dengan: |
||
*[[ |
*[[Garis tinggi segitiga|garis tinggi]], ruas garis dari titik puncak segitiga yang tegak lurus ke alas segitiga;{{sfn|Hadamard|2008|page=23}} |
||
*[[garis bagi sudut]], ruas garis dari puncak ke alas segitiga;{{ |
*[[garis bagi sudut]], ruas garis dari puncak ke alas segitiga;{{sfn|Hadamard|2008|page=23}} |
||
*[[Garis berat (geometri)|garis berat]], ruas garis dari puncak ke titik tengah alas segitiga;{{ |
*[[Garis berat (geometri)|garis berat]], ruas garis dari puncak ke titik tengah alas segitiga;{{sfn|Hadamard|2008|page=23}} |
||
*[[garis bagi tegak lurus|garis bagi |
*[[garis bagi tegak lurus|garis bagi dua tegak lurus]] dari alas dalam segitiga;{{sfn|Hadamard|2008|page=23}} |
||
*ruas garis dalam segitiga dari [[sumbu simetri]] segitiga; dan |
*ruas garis dalam segitiga dari [[sumbu simetri]] segitiga; dan |
||
*ruas garis dalam segitiga dari [[garis Euler]] segitiga, kecuali ketika segitiga [[Segitiga sama sisi|sama sisi]].{{ |
*ruas garis dalam segitiga dari [[garis Euler]] segitiga, kecuali ketika segitiga [[Segitiga sama sisi|sama sisi]].{{sfn|Guinand|1984}} |
||
Secara umum, panjang dari keenam ruas garis tersebut merupakan garis tinggi segitiga <math>h</math>. Jika segitiga mempunyai panjang sisi <math>a</math> yang sama dan panjang alas <math>b</math>, |
Secara umum, panjang dari keenam ruas garis tersebut merupakan garis tinggi segitiga <math>h</math>. Jika segitiga mempunyai panjang sisi <math>a</math> yang sama dan panjang alas <math>b</math>, panjang dari ruas garis tersebut dapat dirumuskan menjadi{{sfn|Harris|Stöcker|1998|page=78}}<math display="block">h=\sqrt{a^2-\frac{b^2}{4}}.</math> |
||
Rumus ini juga dapat diperoleh dari [[teorema Pythagoras]], dengan menggambarkan garis tinggi segitiga yang membagi alas menjadi dua, serta membagi segitiga sama kaki menjadi dua segitiga siku-siku yang kongruen.{{ |
Rumus ini juga dapat diperoleh dari [[teorema Pythagoras]], dengan menggambarkan garis tinggi segitiga yang membagi alas menjadi dua, serta membagi segitiga sama kaki menjadi dua segitiga siku-siku yang kongruen.{{sfn|Salvadori|Wright|1998}} |
||
Garis Euler merupakan garis pada sebarang segitiga yang melalui [[titik tinggi]] segitiga (perpotongan dari tiga garis tinggi segitiga), [[sentroid]] segitiga (perpotongan dari ketiga garis berat segitiga), dan [[Lingkaran luar|pusat lingkaran luar]] segitiga (perpotongan dari garis bagi tegak lurus dengan tiga sisi segitiga, yang juga merupakan pusat lingkaran luar yang melalui tiga buah titik puncak). Dalam segitiga sama kaki dengan tepat memiliki dua sisi yang sama, ketiga titik tersebut berbeda, dan (berdasarkan simetri) semua titik terletak pada simetri sumbu segitiga. Dengan demikian, garis Euler |
Garis Euler merupakan garis pada sebarang segitiga yang melalui [[titik tinggi]] segitiga (perpotongan dari tiga garis tinggi segitiga), [[sentroid]] segitiga (perpotongan dari ketiga garis berat segitiga), dan [[Lingkaran luar|pusat lingkaran luar]] segitiga (perpotongan dari garis bagi tegak lurus dengan tiga sisi segitiga, yang juga merupakan pusat lingkaran luar yang melalui tiga buah titik puncak). Dalam segitiga sama kaki dengan tepat memiliki dua sisi yang sama, ketiga titik tersebut berbeda, dan (berdasarkan simetri) semua titik terletak pada simetri sumbu segitiga. Dengan demikian, garis Euler berimpitan dengan sumbu simetri. [[Pusat dalam]] segitiga juga terletak pada garis Euler, tetapi ini tidak berlaku benar untuk segitiga sama lainnya.{{sfn|Guinand|1984}} Jika ada dua sudut pembagi sebarang, garis berat, atau garis tinggi berimpitan dengan segitiga tersebut, maka segitiga tersebut sama kaki.{{sfn|Hadamard|2008|loc=Latihan 5, hlm. 29}} |
||
===Luas segitiga sama kaki=== |
===Luas segitiga sama kaki=== |
||
Luas segitiga sama kaki <math>T</math> dapat diperoleh dari rumus garis tingginya dan rumus luas segitiga yang umum, yaitu setengah dari hasil kali alas dan tinggi segitiga:{{ |
Luas segitiga sama kaki <math>T</math> dapat diperoleh dari rumus garis tingginya dan rumus luas segitiga yang umum, yaitu setengah dari hasil kali alas dan tinggi segitiga:{{sfn|Harris|Stöcker|1998|page=78}}<math display="block">T=\frac{b}{4}\sqrt{4a^2-b^2}.</math> |
||
Rumus yang sama pula didapatkan dari [[rumus Heron]], luas segitiga yang dihitung dengan menggunakan ketiga sisinya. |
Rumus yang sama pula didapatkan dari [[rumus Heron]], luas segitiga yang dihitung dengan menggunakan ketiga sisinya. Akan tetapi, menerapkan rumus Heron secara langsung dapat menyebabkan [[ketidakstabilan secara numerik]] untuk segitiga sama kaki dengan sudut yang sangat lancip, karena [[semiperimeter]] dan panjang sisi yang saling berdekatan dalam segitiga tersebut.{{sfn|Kahan|2014}} |
||
Jika sudut puncak <math>(\theta)</math> dan panjang kaki <math>(a)</math> dari segitiga sama kaki diketahui, maka luas segitiga sama dengan{{ |
Jika sudut puncak <math>(\theta)</math> dan panjang kaki <math>(a)</math> dari segitiga sama kaki diketahui, maka luas segitiga sama dengan{{sfn|Young|2011|page=298}}<math display="block">T=\frac{1}{2}a^2\sin\theta.</math>Rumus di atas merupakan kasus istimewa dari rumus umum luas segitiga, yaitu setengah dari hasil kali antara dua sisi dengan fungsi sinus dari sudut yang diapit.{{sfn|Young|2011|page=398}} |
||
===Keliling segitiga sama kaki=== |
===Keliling segitiga sama kaki=== |
||
Keliilng segitiga sama kaki <math>p</math> dengan sisi <math>a</math> dan alas segitiga <math>b</math> dirumuskan dengan{{ |
Keliilng segitiga sama kaki <math>p</math> dengan sisi <math>a</math> dan alas segitiga <math>b</math> dirumuskan dengan{{sfn|Harris|Stöcker|1998|page=78}}<math display="block">p = 2a + b.</math>Luas <math>T</math> dan keliling <math>p</math> pada sebarang segitiga berkaitan dengan [[pertidaksamaan isoperimetrik]]{{sfn|Alsina|Nelsen|2009|page=71}}<math display="block">p^2>12\sqrt{3}T.</math> |
||
Pertidaksamaan ini merupakan ''strict inequality'' untuk segitiga sama kaki dengan sisi yang tidak sama dengan alasnya, dan menjadi suatu persamaan untuk segitiga sama sisi. Luas, keliling, dan alasnya juga berkaitan satu sama lain melalui persamaan berikut.{{ |
Pertidaksamaan ini merupakan pertidaksamaan sempurna (''strict inequality'') untuk segitiga sama kaki dengan sisi yang tidak sama dengan alasnya, dan menjadi suatu persamaan untuk segitiga sama sisi. Luas, keliling, dan alasnya juga berkaitan satu sama lain melalui persamaan berikut.{{sfn|Baloglou|Helfgott|2008|loc=Persamaan (1)}}<math display="block">2pb^3 -p^2b^2 + 16T^2 = 0.</math> |
||
Jika alas dan kelilingnya konstan, maka rumus ini menentukan luas dari segitiga sama kaki yang dihasilkan, |
Jika alas dan kelilingnya konstan, maka rumus ini menentukan luas dari segitiga sama kaki yang dihasilkan, yang merupakan nilai maksimum yang mungkin di antara semua segitiga dengan alas dan keliling yang sama.{{sfn|Wickelgren|2012}} Di sisi lain, jika luas dan kelilingnya konstan, maka rumus ini dapat dipakai untuk memperoleh kembali panjang alas, tetapi tidak dilakukan secara khusus karena umumnya ada dua segitiga berbeda yang dinyatakan sebagai luas <math>T</math> dan keliling <math>p</math>. Ketika pertidaksamaan isoperimetrik menjadi persamaan, maka hanya ada satu buah segitiga sama sisi.{{sfn|Baloglou|Helfgott|2008|loc=Teorema 2}} |
||
===Panjang garis bagi sudut=== |
===Panjang garis bagi sudut=== |
||
Jika dua sudut yang sama mempunyai panjang <math>a</math> dan sisi lainnya mempunyai panjang <math>b</math>, maka [[ |
Jika dua sudut yang sama mempunyai panjang <math>a</math> dan sisi lainnya mempunyai panjang <math>b</math>, maka [[garis bagi]] sudut dalam <math>t</math> dari salah satu dari dua titik puncak yang bersudutkan siku-siku memenuhi pertidaksamaan{{sfn|Arslanagić}}<math display="block">\frac{2ab}{a+b} > t > \frac{ab\sqrt{2}}{a+b}</math>dan juga memenuhi<math display="block">t<\frac{4a}{3}.</math> |
||
Sebaliknya, jika syarat pertidaksamaan di atas berlaku, maka segitiga sama kaki yang terparameterisasi oleh <math>a</math> dan <math>t</math> ada.{{ |
Sebaliknya, jika syarat pertidaksamaan di atas berlaku, maka segitiga sama kaki yang terparameterisasi oleh <math>a</math> dan <math>t</math> ada.{{sfn|Oxman|2005}} |
||
[[Teorema Steiner–Lehmus]] mengatakan bahwa setiap segitiga dengan dua garis bagi sudut dengan panjang yang sama adalah sama kaki. Teorema ini dirumuskan oleh [[C. L. Lehmus]] pada tahun 1840. [[Jakob Steiner]], nama lain dari teorema tersebut, adalah salah satu matematikawan yang pertama kali menyediakan solusi dari teorema tersebut.{{ |
[[Teorema Steiner–Lehmus]] mengatakan bahwa setiap segitiga dengan dua garis bagi sudut dengan panjang yang sama adalah sama kaki. Teorema ini dirumuskan oleh [[C. L. Lehmus]] pada tahun 1840. [[Jakob Steiner]], nama lain dari teorema tersebut, adalah salah satu matematikawan yang pertama kali menyediakan solusi dari teorema tersebut.{{sfn|Gilbert|MacDonnell|1963}} Walaupun pada awalnya dirumuskan hanya untuk garis bagi dalam, teorema tersebut bekerja untuk banyak (tapi tidak semua) kasus ketika dua garis bagi sudut luar adalah sama panjang. Segitiga sama kaki 30-30-120 membuat kasus batas untuk variasi teorema ini, karena segitiga tersebut mempunyai empat garis bagi sudut yang sama (dua garis bagi sudut dalam, dan dua garis bagi sudut luar).{{sfn|Conway|Ryba|2014}} |
||
===Jari-jari=== |
===Jari-jari=== |
||
[[File:Isosceles-triangle-more.svg|thumb|Segitiga sama kaki memperlihatkan pusat lingkaran luar (biru), titik berat (merah), pusat dalam (hijau), dan sumbu simetri (ungu)]] |
[[File:Isosceles-triangle-more.svg|thumb|Segitiga sama kaki memperlihatkan pusat lingkaran luar (biru), titik berat (merah), pusat dalam (hijau), dan sumbu simetri (ungu)]] |
||
Rumus jari-jari dalam dan jari-jari luar untuk segitiga sama kaki dapat diperoleh dari rumus jari-jari dalam dan jari-jari luar untuk sebarang segitiga.{{ |
Rumus jari-jari dalam dan jari-jari luar untuk segitiga sama kaki dapat diperoleh dari rumus jari-jari dalam dan jari-jari luar untuk sebarang segitiga.{{sfn|Harris|Stöcker|1998|page=75}} Jari-jari [[lingkaran dalam]] dari segitiga sama kaki dengan panjang sisi <math>a</math>, alas <math>b</math>, dan tinggi <math>h</math> sama dengan{{sfn|Harris|Stöcker|1998|page=78}}<math display="block">\frac{2ab-b^2}{4h}.</math> |
||
Pusat lingkaran terletak pada sumbu simetri segitiga. Segitiga sama kaki mempunyai lingkaran dalam terbesar di antara segitiga lainnya dengan alas dan sudut puncak yang sama. Segitiga sama kaki juga mempunyai luas dan keliling di antara kelas segitiga yang sama.{{ |
Pusat lingkaran terletak pada sumbu simetri segitiga. Segitiga sama kaki mempunyai lingkaran dalam terbesar di antara segitiga lainnya dengan alas dan sudut puncak yang sama. Segitiga sama kaki juga mempunyai luas dan keliling di antara kelas segitiga yang sama.{{sfn|Alsina|Nelsen|2009|page=67}} |
||
Jari-jari [[lingkaran luar]] sama dengan:{{ |
Jari-jari [[lingkaran luar]] sama dengan:{{sfn|Harris|Stöcker|1998|page=78}}<math display="block">\frac{a^2}{2h}.</math> |
||
===Persegi dalam=== |
===Persegi dalam=== |
||
Untuk sebarang segitiga sama kaki, terdapat satu buah persegi dengan sisinya kolinear dengan alas segitiga, dan dengan dua buah titik pojok persegi yang berhadapan dengan sisi segitiga. [[Segitiga Calabi]] merupakan segitiga sama kaki istimewa yang memiliki sifat bahwa dua buah persegi dalam lainnya, dengan sisinya kolinear dengan sisi segitiga, mempunyai ukuran yang sama dengan alas persegi.{{ |
Untuk sebarang segitiga sama kaki, terdapat satu buah persegi dengan sisinya kolinear (segaris) dengan alas segitiga, dan dengan dua buah titik pojok persegi yang berhadapan dengan sisi segitiga. [[Segitiga Calabi]] merupakan segitiga sama kaki istimewa yang memiliki sifat bahwa dua buah persegi dalam lainnya, dengan sisinya kolinear dengan sisi segitiga, mempunyai ukuran yang sama dengan alas persegi.{{sfn|Conway|Guy|1996}} [[Heron dari Iskandariyah|Hero dari Iskandariyah]] menyediakan teorema yang lebih lama. Teorema tersebut mengatakan bahwa untuk sebarang segitiga sama kaki dengan alas <math>b</math> dan tinggi <math>h</math>, maka panjang sisi dari persegi dalam pada alas segitiga sama dengan{{sfn|Gandz|1940}}<math display="block">\frac{bh}{b+h}.</math> |
||
==Subpembagian sama kaki dari bangun lainnya== |
|||
==Pembagian pisah sebarang bangun menjadi segitiga sama kaki== |
|||
[[File:Cyclic pentagon isosceles partition.svg|thumb|Pembagian [[Poligon siklik|segilima siklik]] menjadi segitiga sama kaki melalui jari-jari lingkaran luarnya]] |
[[File:Cyclic pentagon isosceles partition.svg|thumb|Pembagian [[Poligon siklik|segilima siklik]] menjadi segitiga sama kaki melalui jari-jari lingkaran luarnya]] |
||
Untuk sebarang bilangan bulat <math>n \ge 4</math>, maka sebarang [[segitiga]] dapat dibagi menjadi <math>n</math> segitiga sama kaki.<ref>{{ |
Untuk sebarang bilangan bulat <math>n \ge 4</math>, maka sebarang [[segitiga]] dapat dibagi menjadi <math>n</math> segitiga sama kaki.<ref>{{harvnb|Lord|1982}}. Lihat {{harvnb|Hadamard|2008|loc=Latihan 340, hlm. 270}}.</ref> Dalam [[segitiga siku-siku]], garis berat dari hipotenusa (yaitu, ruas garis dari titik tengah suatu hipotenusa ke titik sudut yang berupa siku-siku) membagi segitiga siku-siku menjadi dua segitiga sama kaki. Hal ini dikarenakan titik tengah suatu hipotenusa merupakan pusat [[lingkaran luar]] dari segitiga siku-siku, dan masing-masing dari dua segitiga yang dibuat melalui pembagian mempunyai dua jari-jari yang sama sebagai dua sisi segitiga.{{sfn|Posamentier|Lehmann|2012|page=24}} Mirip dengan cara sebelumnya, [[segitiga lancip]] dapat dibagi menjadi tiga segitiga sama kaki melalui ruas garis dari pusat lingkaran luarnya,{{sfn|Bezdek|Bisztriczky|2015}} tetapi metode ini tidak dapat dilakukan untuk segitiga tumpul, karena pusat lingkaran luarnya terletak di luar segitiga.{{sfn|Harris|Stöcker|1998|page=75}} |
||
Dengan memperumum |
Dengan memperumum pembagian suatu segitiga lancip, sebarang [[Lingkaran luar|poligon siklik]] yang mempunyai pusat lingkaran luar di dalamnya dapat dibagi menjadi segitiga sama kaki dengan jari-jari dari lingkaran tersebut melalui titik sudutnya. Lebih-lebih, semua jari-jari lingkaran yang mempunyai panjang yang sama menyiratkan bahwa semua segitiga di dalamnya adalah sama kaki. Pembagian bangun tersebut dapat dipakai untuk mendapatkan rumus luas poligon sebagai suatu fungsi dari panjang sisinya, bahkan dapat dipakai untuk poligon siklik yang tidak mempunyai pusat lingkaran luar di dalamnya. Rumus tersebut merupakan perumuman dari [[rumus Heron]] untuk segitiga dan [[rumus Brahmagupta]] untuk [[segi empat siklik]].{{sfn|Robbins|1995}} |
||
[[ |
[[Diagonal|Sisi diagonal]] [[belah ketupat]] membaginya menjadi dua segitiga sama kaki yang [[kongruen]]. Mirip dengan cara yang serupa, salah satu dari dua sisi diagonal [[Layang-layang (geometri)|layang-layang]] membaginya menjadi dua segitiga sama kaki, tetapi sayangnya tidak kongruen kecuali ketika bentuknya berupa belah ketupat.{{sfn|Usiskin|Griffin|2008|page=51}} |
||
==Penerapan== |
==Penerapan== |
||
| Baris 120: | Baris 123: | ||
| caption1 = Pedimen pada [[Pantheon, Roma]], berbentuk segitiga tumpul sama kaki |
| caption1 = Pedimen pada [[Pantheon, Roma]], berbentuk segitiga tumpul sama kaki |
||
| image2 = Cathédrale Notre-Dame - Portail du transept sud, dit portail Saint-Etienne, Gables, côté droit - Paris 04 - Médiathèque de l'architecture et du patrimoine - APMH00021092.jpg |
| image2 = Cathédrale Notre-Dame - Portail du transept sud, dit portail Saint-Etienne, Gables, côté droit - Paris 04 - Médiathèque de l'architecture et du patrimoine - APMH00021092.jpg |
||
| caption2 = Atap pelana |
| caption2 = Atap pelana di atas gerbang Saint-Etienne, [[Notre-Dame de Paris]], berbentuk segitiga sama kaki. |
||
}} |
}} |
||
Segitiga sama kaki sering ditemukan di dalam [[arsitektur]] seperti [[atap pelana]] dan [[pedimen]]. Segitiga tumpul sama kaki dipakai dalam [[arsitektur Yunani kuno]] beserta tiruan sebelumnya, tetapi diganti dengan segitiga lancip sama kaki dalam [[arsitektur Gotik]].{{ |
Segitiga sama kaki sering ditemukan di dalam [[arsitektur]] seperti [[atap pelana]] dan [[pedimen]]. Segitiga tumpul sama kaki dipakai dalam [[arsitektur Yunani kuno]] beserta tiruan sebelumnya, tetapi diganti dengan segitiga lancip sama kaki dalam [[arsitektur Gotik]].{{sfn|Lardner|1840|page=46}} |
||
Adapun bentuk segitiga sama kaki lainnya dalam [[Arsitektur Abad Pertengahan|arsitektur pada masa Abad Pertengahan]], yaitu segitiga sama kaki Mesir. Segitiga tersebut |
Adapun bentuk segitiga sama kaki lainnya dalam [[Arsitektur Abad Pertengahan|arsitektur pada masa Abad Pertengahan]], yaitu segitiga sama kaki Mesir. Segitiga tersebut memiliki sudut tumpul, tetapi menyerupai segitiga sama sisi, dan tingginya sebanding dengan 5/8 dari alasnya.{{sfn|Lavedan|1947}} Segitiga sama kaki Mesir telah dibawa kembali ke penggunaannya dalam arsitektur modern oleh [[Hendrik Petrus Berlage]], seorang arsitek asal Belanda.{{sfn|Padovan|2002}} |
||
[[File: DETAIL VIEW OF MODIFIED WARREN TRUSS WITH VERTICALS. - Union Station Viaduct, Spanning Gaspee, Francis, Promenade and Canal Streets, Providence, Providence County, RI HAER RI,4-PROV,179-12.tif|thumb|Gambaran mengenai [[tiang penopang Warren]] yang dimodifikasi dengan tiang vertikal.]] |
[[File: DETAIL VIEW OF MODIFIED WARREN TRUSS WITH VERTICALS. - Union Station Viaduct, Spanning Gaspee, Francis, Promenade and Canal Streets, Providence, Providence County, RI HAER RI,4-PROV,179-12.tif|thumb|Gambaran mengenai [[tiang penopang Warren]] yang dimodifikasi dengan tiang vertikal.]] |
||
Struktur [[tiang penopang Warren]] biasanya disusun berupa segitiga sama kaki, walaupun terkadang terdapat tiang vertikal yang juga dipakai sebagai penopang struktur tersebut.{{ |
Struktur [[tiang penopang Warren]] biasanya disusun berupa segitiga sama kaki, walaupun terkadang terdapat tiang vertikal yang juga dipakai sebagai penopang struktur tersebut.{{sfn|Ketchum|1920}} Permukaan yang [[Teselasi|berpolakan]] segitiga sama kaki tumpul dapat dipakai untuk membentuk [[struktur deployable|struktur ''deployable'']]. Struktur tersebut mempunyai dua keadaan stabil: permukaan pada struktur dengan keadaan yang tidak dilipat diperpanjang menjadi tiang yang berbentuk tabung<u>,</u> dan struktur dengan keadaan lipat yang melipatnya menjadi bentuk prisma yang lebih kompak sehingga dapat diangkut dengan mudah.{{sfn|Pellegrino|2002}} Pola pengubinan yang sama membentuk alas [[tekukan Yoshimura]] (''Yoshimura buckling''), suatu pola yang dibentuk ketika permukaan tabung ditekan secara aksial.{{sfn|Yoshimura|1955}} Pola tersebut juga membentuk [[lentera Schwarz]], suatu contoh yang dipakai dalam matematika untuk memperlihatkan bahwa luas dari permukaan mulus tidak selalu dapat diaproksimasi dengan akurat oleh polihedron yang konvergen menuju permukaannya.{{sfn|Schwarz|1890}} |
||
{{multiple image |
{{multiple image |
||
| Baris 138: | Baris 141: | ||
}} |
}} |
||
Dalam [[desain grafis]] dan [[seni dekoratif]], segitiga sama kaki seringkali dipakai dalam budaya di seluruh dunia |
Dalam [[desain grafis]] dan [[seni dekoratif]], segitiga sama kaki seringkali dipakai dalam budaya di seluruh dunia. Pemakaian tersebut setidaknya berawal dari masa [[Neolitikum#Awal Neolitikum|awal Neolitikum]]{{sfn|Washburn|1984}} hingga ke zaman modern.{{sfn|Jakway|1922}} Segitiga sama kaki biasanya menggambarkan elemen desain dalam [[bendera]] dan [[heraldik]]. Contohnya seperti [[bendera Guyana]] dengan alasnya yang vertikal, atau alasnya yang horizontal seperti [[bendera Saint Lucia]], yang menggambarkan pulau gunung.{{sfn|Smith|2014}} |
||
Segitiga sama kaki juga mempunyai kegunaan dalam agama ataupun hal-hal mistik, seperti [[Wajrayana|meditasi]] [[Sri Yantra]] dalam agama Hindu.{{ |
Segitiga sama kaki juga mempunyai kegunaan dalam agama ataupun hal-hal mistik, seperti [[Wajrayana|meditasi]] [[Sri Yantra]] dalam agama Hindu.{{sfn|Bolton|Nicol|Macleod|1977}} |
||
===Dalam cabang selain matematika=== |
===Dalam cabang selain matematika=== |
||
Jika [[persamaan kubik]] dengan koefisien real mempunyai tiga akar penyelesaian yang bukan [[bilangan real]], maka ketiga akar-akar tersebut digambarkan dalam [[bidang kompleks]] sebagai [[diagram Argand]], dan membentuk titik puncak segitiga sama kaki yang sumbu simetrinya |
Jika [[persamaan kubik]] dengan koefisien real mempunyai tiga akar penyelesaian yang bukan [[bilangan real]], maka ketiga akar-akar tersebut digambarkan dalam [[bidang kompleks]] sebagai [[diagram Argand]], dan membentuk titik puncak segitiga sama kaki yang sumbu simetrinya berimpitan dengan sumbu (real) horizontal. Hal ini dikarenakan akar kompleks merupakan [[konjugat kompleks]] sehingga akar kompleks simetri terhadap sumbu real.{{sfn|Bardell|2016}} |
||
Di dalam [[mekanika benda langit]], [[masalah tiga benda]] telah dikaji dalam kasus istimewa. Ketiga benda tersebut membentuk suatu segitiga sama kaki, karena dengan mengasumsi bahwa benda-benda disusun sedemikian rupa akan mengurangi jumlah [[derajat kebebasan]] dari sistem tanpa mereduksinya ke kasus [[titik Lagrangian]] terselesaikan ketika benda-benda tersebut membentuk segitiga sama sisi. Contoh pertama terkait masalah tiga benda yang diperlihatkan mempunyai alunan tak terbatas dapat ditemukan di dalam masalah tiga benda sama kaki.{{sfn|Diacu|Holmes|1999}} |
|||
==Sejarah dan kekeliruan== |
==Sejarah dan kekeliruan== |
||
Praktisi matematika asal [[Matematikawan Mesir kuno|Mesir kuno]] dan [[Matematikawan Babilonia|Babilonia]] sudah mengetahui bagaimana cara menghitung luas dari segitiga sama kaki, jauh sebelum [[Matematikawan Yunani|matematikawan Yunani kuno]] mempelajari segitiga sama kaki. Masalah-masalah tentang jenis ini tercatat di [[Papirus Matematika Moskow]] dan [[Papirus Matematika Rhind]].<ref>{{ |
Praktisi matematika asal [[Matematikawan Mesir kuno|Mesir kuno]] dan [[Matematikawan Babilonia|Babilonia]] sudah mengetahui bagaimana cara menghitung luas dari segitiga sama kaki, jauh sebelum [[Matematikawan Yunani|matematikawan Yunani kuno]] mempelajari segitiga sama kaki. Masalah-masalah tentang jenis ini tercatat di dalam [[Papirus Matematika Moskow]] dan [[Papirus Matematika Rhind]].<ref>{{harvnb|Høyrup}}. "Banyak Egiptolog sebelumnya" percaya bahwa bangsa Mesir menggunakan rumus tentang luas segitiga yang kurang tepat, yang berbunyi hasil kali dari alas dengan sisi. Walaupun demikian, [[Vasily Vasilievich Struve|Vasily]] mendukung pandangan tersebut bahwa bangsa Mesir menggunakan rumus yang benar, yaitu hasil kali dari alas dengan sisi {{harvnb|Clagett|1989}}. Hal ini menimbulkan sisa pertanyaan mengenai terjemahan dari salah satu kata yang terdapat di dalam papirus Rhind, dan kata tersebut diterjemahkan sebagai tinggi (atau lebih tepatnya sebagai perbandingan tinggi dengan alas), sehingga rumus tersebut benar {{harvnb|Gunn|Peet|1929|pages=173–174}}.</ref> |
||
Teorema yang mengatakan bahwa sudut alas suatu segitiga sama kaki terdapat di [[Elemen Euklides|''Euclid'']], Proposisi I.5,{{ |
Teorema yang mengatakan bahwa sudut alas suatu segitiga sama kaki terdapat di [[Elemen Euklides|''Euclid'']], Proposisi I.5,{{sfn|Heath|1956|loc=hlm. 251}} dan hasil dari teorema itu disebut ''[[pons asinorum]]'' (berarti jembatan keledai) atau teorema segitiga sama kaki. Penjelasan yang mirip dengan namanya memuat sebuah teori, yang dikarenakan Euklides menggunakan diagram dalam hasil buktinya menyerupai sebuah jembatan, atau dikarenakan hasil pertama miliknya yang sangat sulit. Oleh sebab itu, hasil tersebut dipisahkan kepada orang yang memahami geometri Euklides dan kepada orang yang tidak memahaminya.{{sfn|Venema|2006|loc=hlm. 89}} |
||
Ada sebuah bukti [[Kekeliruan dalam matematika#Geometri|kekeliruan]] terkenal yang mengatakan bahwa ''semua segitiga adalah sama kaki''. [[Robin Wilson (matematikawan)|Robin Wilson]] mengaitkan argumen tersebut dengan [[Lewis Carroll]],{{ |
Ada sebuah bukti [[Kekeliruan dalam matematika#Geometri|kekeliruan]] terkenal yang mengatakan bahwa ''semua segitiga adalah sama kaki''. [[Robin Wilson (matematikawan)|Robin Wilson]] mengaitkan argumen tersebut dengan [[Lewis Carroll]],{{sfn|Wilson|2008}} yang menerbitkannya pada tahun 1899, tetapi [[W. W. Rouse Ball]] menerbitkannya pada tahun 1892 dan kemudian menuliskan bahwa Carroll memperoleh argumen darinya.{{sfn|Ball|Coxeter|1987}} Kekeliruan tersebut terjadi ketika Eukildes gagal memahami konsep "keantaraan" (''betweenness'') sehingga mengakibatkan kedwiartian dari kata ''di dalam'' dan ''di luar'' bangun.{{sfn|Specht|Jones|Calkins|Rhoads|2015}} |
||
==Catatan== |
==Catatan== |
||
| Baris 279: | Baris 282: | ||
| title = Studies in Babylonian mathematics. III. Isoperimetric problems and the origin of the quadratic equations |
| title = Studies in Babylonian mathematics. III. Isoperimetric problems and the origin of the quadratic equations |
||
| volume = 32 |
| volume = 32 |
||
| year = 1940}}. See in particular p. |
| year = 1940}}. See in particular p. 111. |
||
*{{citation |
*{{citation |
||
| last1 = Gilbert | first1 = G. |
| last1 = Gilbert | first1 = G. |
||
| Baris 558: | Baris 561: | ||
{{Poligon}} |
{{Poligon}} |
||
[[Kategori:Jenis segitiga]] |
[[Kategori:Jenis segitiga]] |
||
Revisi terkini sejak 12 Oktober 2023 03.49
| Segitiga sama kaki | |
|---|---|
 | |
| Jenis | Segitiga |
| Sisi dan titik pojok | 3 |
| Simbol Schläfli | ( ) ∨ { } |
| Grup simetri | Dih2, [ ], (*), orde 2 |
| Sifat | cembung, siklik |
Dalam geometri, segitiga sama kaki (bahasa Inggris: isosceles triangle) adalah segitiga yang memiliki dua sisi yang sama panjangnya. Segitiga ini terkadang dinyatakan memiliki tepat dua sisi yang sama panjang. Segitiga ini juga terkadang dinyatakan setidaknya mempunyai dua sisi yang sama panjang, dan pernyataan ini meliputi segitiga sama sisi sebagai kasus istimewa. Contoh-contoh segitiga sama kaki di antaranya segitiga siku-siku sama kaki, segitiga emas, serta muka yang terdapat di bipiramida dan bangun ruang Catalan.
Kajian matematika tentang segitiga sama kaki berawal dari matematika Mesir kuno dan matematika Babilonia. Segitiga sama kaki bahkan dipakai sebagai hiasan pada masa sebelumnya. Segitiga ini sering ditemukan dalam arsitektur dan desain, seperti pedimen dan atap pelana bangunan.
Segitiga sama kaki mempunyai dua sisi yang sama panjang yang disebut kaki, sementara sisi ketiganya disebut alas segitiga. Dimensi segitiga lain seperti tinggi, luas, dan keliling, dapat dihitung dengan rumus sederhana menggunakan panjang kaki dan alas segitiga. Setiap segitiga sama kaki memiliki sumbu simetri di sepanjang garis bagi yang tegak lurus dari alasnya. Dua sudut yang berhadapan dengan kaki segitiga adalah sama dan selalu lancip, sehingga penggolongan segitiga berupa segitiga lancip, siku-siku, atau tumpul, hanya bergantung pada sudut yang diapit oleh dua kaki segitiga.
Penggolongan dan sudut segitiga
Euklides mendefinisikan segitiga sama kaki sebagai segitiga yang tepat memiliki dua sisi yang sama panjang,[1] sedangkan penjelasan modern lebih mendefinisikan segitiga sama kaki sebagai segitiga yang setidaknya memiliki dua sisi yang sama panjang. Perbedaan dari kedua definisi tersebut adalah bahwa definisi dari versi modern meliputi segitiga sama sisi (dengan panjang dari ketiga sisinya sama) sebagai kasus istimewa dari segitiga sama kaki.[2] Segitiga yang bukan sama kaki (dengan panjang dari ketiga sisinya tidak sama) disebut segitiga sembarang.[3]
Dalam segitiga sama kaki yang memiliki tepat dua sisi yang sama, sisi yang sama disebut kaki dan sisi ketiga disebut alas. Sudut yang diapit oleh kedua sisi disebut sudut puncak (vertex angle), sedangkan sudut yang diapit oleh alas segitiga dan salah satu sisi lainnya disebut sudut alas (base angle).[4] Titik yang berhadapan dengan alas segitiga disebut titik puncak segitiga.[5] Dalam kasus segitiga sama sisi, karena semua sisi segitiga adalah sama, maka sebarang sisi dapat dikatakan sebagai alas.[6]
Penggolongan segitiga sama kaki dapat menjadi lancip, siku-siku, ataupun tumpul hanya tergantung sudut puncaknya. Dalam geometri Euklides, sudut alas segitiga tidak tumpul (lebih besar dari 90°) atau siku-siku (sama dengan 90°) karena sudutnya sama dengan jumlah sudut dalam dari sebarang segitiga, yaitu 180°.[6] Karena segitiga merupakan segitiga tumpul atau siku-siku jika dan hanya jika salah satu sudutnya tumpul atau siku-siku, maka segitiga sama kaki dapat berupa segitiga tumpul, siku-siku, atau lancip jika dan hanya jika sudut puncaknya adalah tumpul, siku-siku, atau lancip.[5] Penggolongan segitiga sama kaki dan bangun datar umumnya dipakai Edwin Abbott dalam novel Flatland sebagai sindiran tentang hierarki sosial, contohnya segitiga sama kaki yang menyatakan kelas pekerja, dengan segitiga lancip sama kaki menyatakan tingkat yang lebih tinggi daripada segitiga sama kaki siku-siku ataupun tumpul.[7]
Selain segitiga siku-siku sama kaki, ada beberapa bangun segitiga sama kaki spesifik lainnya juga dikaji. Segitiga tersebut di antaranya segitiga Calabi (segitiga yang memiliki tiga persegi dalam yang kongruen),[8] segitiga emas dan gnomon emas (dua segitiga sama kaki yang perbandingan antara panjang sisi dengan alasnya bernilai rasio emas),[9] segitiga dengan sudut 80-80-20 ditemukan dalam teka-teki Langley's Adventitious Angles,[10] dan segitiga dengan sudut 30-30-120 ditemukan dalam pengubinan segitiga triakis. Masing-masing kelima bangun ruang Catalan, yaitu tetrahedron triakis, oktahedron triakis, heksahedron triakis, dodekahedron pentakis, dan ikosahedron triakis, mempunyai muka berbentuk segitiga sama kaki; sama halnya dengan tak berhingga banyaknya limas[6] dan bipiramida.[11]
Rumus
Garis tinggi segitiga sama kaki
Untuk sebarang segitiga sama kaki, keenam ruas garis berikut berimpitan dengan:
- garis tinggi, ruas garis dari titik puncak segitiga yang tegak lurus ke alas segitiga;[12]
- garis bagi sudut, ruas garis dari puncak ke alas segitiga;[12]
- garis berat, ruas garis dari puncak ke titik tengah alas segitiga;[12]
- garis bagi dua tegak lurus dari alas dalam segitiga;[12]
- ruas garis dalam segitiga dari sumbu simetri segitiga; dan
- ruas garis dalam segitiga dari garis Euler segitiga, kecuali ketika segitiga sama sisi.[13]
Secara umum, panjang dari keenam ruas garis tersebut merupakan garis tinggi segitiga . Jika segitiga mempunyai panjang sisi yang sama dan panjang alas , panjang dari ruas garis tersebut dapat dirumuskan menjadi[14]
Rumus ini juga dapat diperoleh dari teorema Pythagoras, dengan menggambarkan garis tinggi segitiga yang membagi alas menjadi dua, serta membagi segitiga sama kaki menjadi dua segitiga siku-siku yang kongruen.[15]
Garis Euler merupakan garis pada sebarang segitiga yang melalui titik tinggi segitiga (perpotongan dari tiga garis tinggi segitiga), sentroid segitiga (perpotongan dari ketiga garis berat segitiga), dan pusat lingkaran luar segitiga (perpotongan dari garis bagi tegak lurus dengan tiga sisi segitiga, yang juga merupakan pusat lingkaran luar yang melalui tiga buah titik puncak). Dalam segitiga sama kaki dengan tepat memiliki dua sisi yang sama, ketiga titik tersebut berbeda, dan (berdasarkan simetri) semua titik terletak pada simetri sumbu segitiga. Dengan demikian, garis Euler berimpitan dengan sumbu simetri. Pusat dalam segitiga juga terletak pada garis Euler, tetapi ini tidak berlaku benar untuk segitiga sama lainnya.[13] Jika ada dua sudut pembagi sebarang, garis berat, atau garis tinggi berimpitan dengan segitiga tersebut, maka segitiga tersebut sama kaki.[16]
Luas segitiga sama kaki
Luas segitiga sama kaki dapat diperoleh dari rumus garis tingginya dan rumus luas segitiga yang umum, yaitu setengah dari hasil kali alas dan tinggi segitiga:[14]
Rumus yang sama pula didapatkan dari rumus Heron, luas segitiga yang dihitung dengan menggunakan ketiga sisinya. Akan tetapi, menerapkan rumus Heron secara langsung dapat menyebabkan ketidakstabilan secara numerik untuk segitiga sama kaki dengan sudut yang sangat lancip, karena semiperimeter dan panjang sisi yang saling berdekatan dalam segitiga tersebut.[17]
Jika sudut puncak dan panjang kaki dari segitiga sama kaki diketahui, maka luas segitiga sama dengan[18]Rumus di atas merupakan kasus istimewa dari rumus umum luas segitiga, yaitu setengah dari hasil kali antara dua sisi dengan fungsi sinus dari sudut yang diapit.[19]
Keliling segitiga sama kaki
Keliilng segitiga sama kaki dengan sisi dan alas segitiga dirumuskan dengan[14]Luas dan keliling pada sebarang segitiga berkaitan dengan pertidaksamaan isoperimetrik[20]
Pertidaksamaan ini merupakan pertidaksamaan sempurna (strict inequality) untuk segitiga sama kaki dengan sisi yang tidak sama dengan alasnya, dan menjadi suatu persamaan untuk segitiga sama sisi. Luas, keliling, dan alasnya juga berkaitan satu sama lain melalui persamaan berikut.[21]
Jika alas dan kelilingnya konstan, maka rumus ini menentukan luas dari segitiga sama kaki yang dihasilkan, yang merupakan nilai maksimum yang mungkin di antara semua segitiga dengan alas dan keliling yang sama.[22] Di sisi lain, jika luas dan kelilingnya konstan, maka rumus ini dapat dipakai untuk memperoleh kembali panjang alas, tetapi tidak dilakukan secara khusus karena umumnya ada dua segitiga berbeda yang dinyatakan sebagai luas dan keliling . Ketika pertidaksamaan isoperimetrik menjadi persamaan, maka hanya ada satu buah segitiga sama sisi.[23]
Panjang garis bagi sudut
Jika dua sudut yang sama mempunyai panjang dan sisi lainnya mempunyai panjang , maka garis bagi sudut dalam dari salah satu dari dua titik puncak yang bersudutkan siku-siku memenuhi pertidaksamaan[24]dan juga memenuhi
Sebaliknya, jika syarat pertidaksamaan di atas berlaku, maka segitiga sama kaki yang terparameterisasi oleh dan ada.[25]
Teorema Steiner–Lehmus mengatakan bahwa setiap segitiga dengan dua garis bagi sudut dengan panjang yang sama adalah sama kaki. Teorema ini dirumuskan oleh C. L. Lehmus pada tahun 1840. Jakob Steiner, nama lain dari teorema tersebut, adalah salah satu matematikawan yang pertama kali menyediakan solusi dari teorema tersebut.[26] Walaupun pada awalnya dirumuskan hanya untuk garis bagi dalam, teorema tersebut bekerja untuk banyak (tapi tidak semua) kasus ketika dua garis bagi sudut luar adalah sama panjang. Segitiga sama kaki 30-30-120 membuat kasus batas untuk variasi teorema ini, karena segitiga tersebut mempunyai empat garis bagi sudut yang sama (dua garis bagi sudut dalam, dan dua garis bagi sudut luar).[27]
Jari-jari

Rumus jari-jari dalam dan jari-jari luar untuk segitiga sama kaki dapat diperoleh dari rumus jari-jari dalam dan jari-jari luar untuk sebarang segitiga.[28] Jari-jari lingkaran dalam dari segitiga sama kaki dengan panjang sisi , alas , dan tinggi sama dengan[14]
Pusat lingkaran terletak pada sumbu simetri segitiga. Segitiga sama kaki mempunyai lingkaran dalam terbesar di antara segitiga lainnya dengan alas dan sudut puncak yang sama. Segitiga sama kaki juga mempunyai luas dan keliling di antara kelas segitiga yang sama.[29]
Jari-jari lingkaran luar sama dengan:[14]
Persegi dalam
Untuk sebarang segitiga sama kaki, terdapat satu buah persegi dengan sisinya kolinear (segaris) dengan alas segitiga, dan dengan dua buah titik pojok persegi yang berhadapan dengan sisi segitiga. Segitiga Calabi merupakan segitiga sama kaki istimewa yang memiliki sifat bahwa dua buah persegi dalam lainnya, dengan sisinya kolinear dengan sisi segitiga, mempunyai ukuran yang sama dengan alas persegi.[8] Hero dari Iskandariyah menyediakan teorema yang lebih lama. Teorema tersebut mengatakan bahwa untuk sebarang segitiga sama kaki dengan alas dan tinggi , maka panjang sisi dari persegi dalam pada alas segitiga sama dengan[30]
Pembagian pisah sebarang bangun menjadi segitiga sama kaki

Untuk sebarang bilangan bulat , maka sebarang segitiga dapat dibagi menjadi segitiga sama kaki.[31] Dalam segitiga siku-siku, garis berat dari hipotenusa (yaitu, ruas garis dari titik tengah suatu hipotenusa ke titik sudut yang berupa siku-siku) membagi segitiga siku-siku menjadi dua segitiga sama kaki. Hal ini dikarenakan titik tengah suatu hipotenusa merupakan pusat lingkaran luar dari segitiga siku-siku, dan masing-masing dari dua segitiga yang dibuat melalui pembagian mempunyai dua jari-jari yang sama sebagai dua sisi segitiga.[32] Mirip dengan cara sebelumnya, segitiga lancip dapat dibagi menjadi tiga segitiga sama kaki melalui ruas garis dari pusat lingkaran luarnya,[33] tetapi metode ini tidak dapat dilakukan untuk segitiga tumpul, karena pusat lingkaran luarnya terletak di luar segitiga.[28]
Dengan memperumum pembagian suatu segitiga lancip, sebarang poligon siklik yang mempunyai pusat lingkaran luar di dalamnya dapat dibagi menjadi segitiga sama kaki dengan jari-jari dari lingkaran tersebut melalui titik sudutnya. Lebih-lebih, semua jari-jari lingkaran yang mempunyai panjang yang sama menyiratkan bahwa semua segitiga di dalamnya adalah sama kaki. Pembagian bangun tersebut dapat dipakai untuk mendapatkan rumus luas poligon sebagai suatu fungsi dari panjang sisinya, bahkan dapat dipakai untuk poligon siklik yang tidak mempunyai pusat lingkaran luar di dalamnya. Rumus tersebut merupakan perumuman dari rumus Heron untuk segitiga dan rumus Brahmagupta untuk segi empat siklik.[34]
Sisi diagonal belah ketupat membaginya menjadi dua segitiga sama kaki yang kongruen. Mirip dengan cara yang serupa, salah satu dari dua sisi diagonal layang-layang membaginya menjadi dua segitiga sama kaki, tetapi sayangnya tidak kongruen kecuali ketika bentuknya berupa belah ketupat.[35]
Penerapan
Dalam arsitektur dan desain
Segitiga sama kaki sering ditemukan di dalam arsitektur seperti atap pelana dan pedimen. Segitiga tumpul sama kaki dipakai dalam arsitektur Yunani kuno beserta tiruan sebelumnya, tetapi diganti dengan segitiga lancip sama kaki dalam arsitektur Gotik.[6]
Adapun bentuk segitiga sama kaki lainnya dalam arsitektur pada masa Abad Pertengahan, yaitu segitiga sama kaki Mesir. Segitiga tersebut memiliki sudut tumpul, tetapi menyerupai segitiga sama sisi, dan tingginya sebanding dengan 5/8 dari alasnya.[36] Segitiga sama kaki Mesir telah dibawa kembali ke penggunaannya dalam arsitektur modern oleh Hendrik Petrus Berlage, seorang arsitek asal Belanda.[37]

Struktur tiang penopang Warren biasanya disusun berupa segitiga sama kaki, walaupun terkadang terdapat tiang vertikal yang juga dipakai sebagai penopang struktur tersebut.[38] Permukaan yang berpolakan segitiga sama kaki tumpul dapat dipakai untuk membentuk struktur deployable. Struktur tersebut mempunyai dua keadaan stabil: permukaan pada struktur dengan keadaan yang tidak dilipat diperpanjang menjadi tiang yang berbentuk tabung, dan struktur dengan keadaan lipat yang melipatnya menjadi bentuk prisma yang lebih kompak sehingga dapat diangkut dengan mudah.[39] Pola pengubinan yang sama membentuk alas tekukan Yoshimura (Yoshimura buckling), suatu pola yang dibentuk ketika permukaan tabung ditekan secara aksial.[40] Pola tersebut juga membentuk lentera Schwarz, suatu contoh yang dipakai dalam matematika untuk memperlihatkan bahwa luas dari permukaan mulus tidak selalu dapat diaproksimasi dengan akurat oleh polihedron yang konvergen menuju permukaannya.[41]
Dalam desain grafis dan seni dekoratif, segitiga sama kaki seringkali dipakai dalam budaya di seluruh dunia. Pemakaian tersebut setidaknya berawal dari masa awal Neolitikum[42] hingga ke zaman modern.[43] Segitiga sama kaki biasanya menggambarkan elemen desain dalam bendera dan heraldik. Contohnya seperti bendera Guyana dengan alasnya yang vertikal, atau alasnya yang horizontal seperti bendera Saint Lucia, yang menggambarkan pulau gunung.[44]
Segitiga sama kaki juga mempunyai kegunaan dalam agama ataupun hal-hal mistik, seperti meditasi Sri Yantra dalam agama Hindu.[45]
Dalam cabang selain matematika
Jika persamaan kubik dengan koefisien real mempunyai tiga akar penyelesaian yang bukan bilangan real, maka ketiga akar-akar tersebut digambarkan dalam bidang kompleks sebagai diagram Argand, dan membentuk titik puncak segitiga sama kaki yang sumbu simetrinya berimpitan dengan sumbu (real) horizontal. Hal ini dikarenakan akar kompleks merupakan konjugat kompleks sehingga akar kompleks simetri terhadap sumbu real.[46]
Di dalam mekanika benda langit, masalah tiga benda telah dikaji dalam kasus istimewa. Ketiga benda tersebut membentuk suatu segitiga sama kaki, karena dengan mengasumsi bahwa benda-benda disusun sedemikian rupa akan mengurangi jumlah derajat kebebasan dari sistem tanpa mereduksinya ke kasus titik Lagrangian terselesaikan ketika benda-benda tersebut membentuk segitiga sama sisi. Contoh pertama terkait masalah tiga benda yang diperlihatkan mempunyai alunan tak terbatas dapat ditemukan di dalam masalah tiga benda sama kaki.[47]
Sejarah dan kekeliruan
Praktisi matematika asal Mesir kuno dan Babilonia sudah mengetahui bagaimana cara menghitung luas dari segitiga sama kaki, jauh sebelum matematikawan Yunani kuno mempelajari segitiga sama kaki. Masalah-masalah tentang jenis ini tercatat di dalam Papirus Matematika Moskow dan Papirus Matematika Rhind.[48]
Teorema yang mengatakan bahwa sudut alas suatu segitiga sama kaki terdapat di Euclid, Proposisi I.5,[49] dan hasil dari teorema itu disebut pons asinorum (berarti jembatan keledai) atau teorema segitiga sama kaki. Penjelasan yang mirip dengan namanya memuat sebuah teori, yang dikarenakan Euklides menggunakan diagram dalam hasil buktinya menyerupai sebuah jembatan, atau dikarenakan hasil pertama miliknya yang sangat sulit. Oleh sebab itu, hasil tersebut dipisahkan kepada orang yang memahami geometri Euklides dan kepada orang yang tidak memahaminya.[50]
Ada sebuah bukti kekeliruan terkenal yang mengatakan bahwa semua segitiga adalah sama kaki. Robin Wilson mengaitkan argumen tersebut dengan Lewis Carroll,[51] yang menerbitkannya pada tahun 1899, tetapi W. W. Rouse Ball menerbitkannya pada tahun 1892 dan kemudian menuliskan bahwa Carroll memperoleh argumen darinya.[52] Kekeliruan tersebut terjadi ketika Eukildes gagal memahami konsep "keantaraan" (betweenness) sehingga mengakibatkan kedwiartian dari kata di dalam dan di luar bangun.[53]
Catatan
- ^ Heath 1956, hlm. 187, Definisi 20.
- ^ Stahl 2003, hlm. 37.
- ^ Usiskin & Griffin 2008, hlm. 4.
- ^ Jacobs 1974, hlm. 144.
- ^ a b Gottschau, Haverkort & Matzke 2018.
- ^ a b c d Lardner 1840, hlm. 46.
- ^ Barnes 2012.
- ^ a b Conway & Guy 1996.
- ^ Loeb 1992.
- ^ Langley 1922.
- ^ Montroll 2009.
- ^ a b c d Hadamard 2008, hlm. 23.
- ^ a b Guinand 1984.
- ^ a b c d e Harris & Stöcker 1998, hlm. 78.
- ^ Salvadori & Wright 1998.
- ^ Hadamard 2008, Latihan 5, hlm. 29.
- ^ Kahan 2014.
- ^ Young 2011, hlm. 298.
- ^ Young 2011, hlm. 398.
- ^ Alsina & Nelsen 2009, hlm. 71.
- ^ Baloglou & Helfgott 2008, Persamaan (1).
- ^ Wickelgren 2012.
- ^ Baloglou & Helfgott 2008, Teorema 2.
- ^ Arslanagić.
- ^ Oxman 2005.
- ^ Gilbert & MacDonnell 1963.
- ^ Conway & Ryba 2014.
- ^ a b Harris & Stöcker 1998, hlm. 75.
- ^ Alsina & Nelsen 2009, hlm. 67.
- ^ Gandz 1940.
- ^ Lord 1982. Lihat Hadamard 2008, Latihan 340, hlm. 270.
- ^ Posamentier & Lehmann 2012, hlm. 24.
- ^ Bezdek & Bisztriczky 2015.
- ^ Robbins 1995.
- ^ Usiskin & Griffin 2008, hlm. 51.
- ^ Lavedan 1947.
- ^ Padovan 2002.
- ^ Ketchum 1920.
- ^ Pellegrino 2002.
- ^ Yoshimura 1955.
- ^ Schwarz 1890.
- ^ Washburn 1984.
- ^ Jakway 1922.
- ^ Smith 2014.
- ^ Bolton, Nicol & Macleod 1977.
- ^ Bardell 2016.
- ^ Diacu & Holmes 1999.
- ^ Høyrup. "Banyak Egiptolog sebelumnya" percaya bahwa bangsa Mesir menggunakan rumus tentang luas segitiga yang kurang tepat, yang berbunyi hasil kali dari alas dengan sisi. Walaupun demikian, Vasily mendukung pandangan tersebut bahwa bangsa Mesir menggunakan rumus yang benar, yaitu hasil kali dari alas dengan sisi Clagett 1989. Hal ini menimbulkan sisa pertanyaan mengenai terjemahan dari salah satu kata yang terdapat di dalam papirus Rhind, dan kata tersebut diterjemahkan sebagai tinggi (atau lebih tepatnya sebagai perbandingan tinggi dengan alas), sehingga rumus tersebut benar Gunn & Peet 1929, hlm. 173–174.
- ^ Heath 1956, hlm. 251.
- ^ Venema 2006, hlm. 89.
- ^ Wilson 2008.
- ^ Ball & Coxeter 1987.
- ^ Specht et al. 2015.
Rujukan
- Alsina, Claudi; Nelsen, Roger B. (2009), When less is more: Visualizing basic inequalities, The Dolciani Mathematical Expositions, 36, Mathematical Association of America, Washington, DC, ISBN 978-0-88385-342-9, MR 2498836
- Arslanagić, Šefket, "Problem η44", Inequalities proposed in Crux Mathematicorum (PDF), hlm. 151
- Ball, W. W. Rouse; Coxeter, H. S. M. (1987) [1892], Mathematical Recreations and Essays (edisi ke-13th), Dover, footnote, p. 77, ISBN 0-486-25357-0
- Baloglou, George; Helfgott, Michel (2008), "Angles, area, and perimeter caught in a cubic" (PDF), Forum Geometricorum, 8: 13–25, MR 2373294
- Bardell, Nicholas S. (2016), "Cubic polynomials with real or complex coefficients: The full picture" (PDF), Australian Senior Mathematics Journal, 30 (2): 5–26
- Barnes, John (2012), Gems of Geometry (edisi ke-2nd, illustrated), Springer, hlm. 27, ISBN 9783642309649
- Bezdek, András; Bisztriczky, Ted (2015), "Finding equal-diameter triangulations in polygons", Beiträge zur Algebra und Geometrie, 56 (2): 541–549, doi:10.1007/s13366-014-0206-6, MR 3391189
- Bolton, Nicholas J; Nicol, D.; Macleod, G. (March 1977), "The geometry of the Śrī-yantra", Religion, 7 (1): 66–85, doi:10.1016/0048-721x(77)90008-2
- Clagett, Marshall (1989), Ancient Egyptian Science: Ancient Egyptian mathematics, American Philosophical Society, Footnote 68, pp. 195–197, ISBN 9780871692320
- Conway, J.H.; Guy, R.K. (1996), "Calabi's Triangle", The Book of Numbers, New York: Springer-Verlag, hlm. 206
- Conway, John; Ryba, Alex (July 2014), "The Steiner–Lehmus angle-bisector theorem", The Mathematical Gazette, 98 (542): 193–203, doi:10.1017/s0025557200001236
- Diacu, Florin; Holmes, Philip (1999), Celestial Encounters: The Origins of Chaos and Stability, Princeton Science Library, Princeton University Press, hlm. 122, ISBN 9780691005454
- Gandz, Solomon (1940), "Studies in Babylonian mathematics. III. Isoperimetric problems and the origin of the quadratic equations", Isis, 32: 101–115 (1947), doi:10.1086/347645, MR 0017683. See in particular p. 111.
- Gilbert, G.; MacDonnell, D. (1963), "The Steiner–Lehmus Theorem", Classroom Notes, American Mathematical Monthly, 70 (1): 79–80, doi:10.2307/2312796, MR 1531983
- Gottschau, Marinus; Haverkort, Herman; Matzke, Kilian (2018), "Reptilings and space-filling curves for acute triangles", Discrete & Computational Geometry, 60 (1): 170–199, arXiv:1603.01382
 , doi:10.1007/s00454-017-9953-0
, doi:10.1007/s00454-017-9953-0 - Guinand, Andrew P. (1984), "Euler lines, tritangent centers, and their triangles", American Mathematical Monthly, 91 (5): 290–300, doi:10.2307/2322671, MR 0740243
- Gunn, Battiscombe; Peet, T. Eric (May 1929), "Four geometrical problems from the Moscow Mathematical Papyrus", The Journal of Egyptian Archaeology, 15 (1): 167–185, doi:10.1177/030751332901500130, JSTOR 3854111
- Hadamard, Jacques (2008), Lessons in Geometry: Plane geometry, diterjemahkan oleh Saul, Mark, American Mathematical Society, ISBN 9780821843673
- Harris, John W.; Stöcker, Horst (1998), Handbook of mathematics and computational science, New York: Springer-Verlag, doi:10.1007/978-1-4612-5317-4, ISBN 0-387-94746-9, MR 1621531
- Heath, Thomas L. (1956) [1925], The Thirteen Books of Euclid's Elements, 1 (edisi ke-2nd), New York: Dover Publications, ISBN 0-486-60088-2
- Høyrup, Jens, "Geometry in Mesopotamia and Egypt", Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, Springer Netherlands, hlm. 1019–1023, doi:10.1007/978-1-4020-4425-0_8619
- Ionin, Yury J. (2009), "Isosceles sets", Electronic Journal of Combinatorics, 16 (1): R141:1–R141:24, doi:10.37236/230
 , MR 2577309
, MR 2577309 - Jacobs, Harold R. (1974), Geometry, W. H. Freeman and Co., ISBN 0-7167-0456-0
- Jakway, Bernard C. (1922), The Principles of Interior Decoration, Macmillan, hlm. 48
- Kahan, W. (September 4, 2014), "Miscalculating Area and Angles of a Needle-like Triangle" (PDF), Lecture Notes for Introductory Numerical Analysis Classes, University of California, Berkeley
- Ketchum, Milo Smith (1920), The Design of Highway Bridges of Steel, Timber and Concrete, New York: McGraw-Hill, hlm. 107
- Langley, E. M. (1922), "Problem 644", The Mathematical Gazette, 11: 173
- Lardner, Dionysius (1840), A Treatise on Geometry and Its Application in the Arts, The Cabinet Cyclopædia, London
- Lavedan, Pierre (1947), French Architecture, Penguin Books, hlm. 44
- Loeb, Arthur (1992), Concepts and Images: Visual Mathematics, Boston: Birkhäuser Boston, hlm. 180, ISBN 0-8176-3620-X
- Lord, N. J. (June 1982), "66.16 Isosceles subdivisions of triangles", The Mathematical Gazette, 66 (436): 136, doi:10.2307/3617750
- Montroll, John (2009), Origami Polyhedra Design, A K Peters, hlm. 6, ISBN 9781439871065
- Oxman, Victor (2005), "On the existence of triangles with given lengths of one side, the opposite and one adjacent angle bisectors" (PDF), Forum Geometricorum, 5: 21–22, MR 2141652
- Padovan, Richard (2002), Towards Universality: Le Corbusier, Mies, and De Stijl, Psychology Press, hlm. 128, ISBN 9780415259620
- Pellegrino, S. (2002), Deployable Structures, CISM International Centre for Mechanical Sciences, 412, Springer, hlm. 99–100, ISBN 9783211836859
- Posamentier, Alfred S.; Lehmann, Ingmar (2012), The Secrets of Triangles: A Mathematical Journey, Amherst, NY: Prometheus Books, hlm. 387, ISBN 978-1-61614-587-3, MR 2963520
- Robbins, David P. (1995), "Areas of polygons inscribed in a circle", American Mathematical Monthly, 102 (6): 523–530, doi:10.2307/2974766, MR 1336638
- Salvadori, Mario; Wright, Joseph P. (1998), Math Games for Middle School: Challenges and Skill-Builders for Students at Every Level, Chicago Review Press, hlm. 70–71, ISBN 9781569767276
- Schwarz, H. A. (1890), Gesammelte Mathematische Abhandlungen von H. A. Schwarz, Verlag von Julius Springer, hlm. 309–311
- Smith, Whitney (June 26, 2014), "Flag of Saint Lucia", Encyclopædia Britannica, diakses tanggal 2018-09-12
- Specht, Edward John; Jones, Harold Trainer; Calkins, Keith G.; Rhoads, Donald H. (2015), Euclidean geometry and its subgeometries, Springer, Cham, hlm. 64, doi:10.1007/978-3-319-23775-6, ISBN 978-3-319-23774-9, MR 3445044
- Stahl, Saul (2003), Geometry from Euclid to Knots, Prentice-Hall, ISBN 0-13-032927-4
- Usiskin, Zalman; Griffin, Jennifer (2008), The Classification of Quadrilaterals: A Study in Definition, Research in Mathematics Education, Information Age Publishing, ISBN 9781607526001
- Venema, Gerard A. (2006), Foundations of Geometry, Prentice-Hall, ISBN 0-13-143700-3
- Washburn, Dorothy K. (July 1984), "A study of the red on cream and cream on red designs on Early Neolithic ceramics from Nea Nikomedeia", American Journal of Archaeology, 88 (3): 305, doi:10.2307/504554
- Wickelgren, Wayne A. (2012), How to Solve Mathematical Problems, Dover Books on Mathematics, Courier Corporation, hlm. 222–224, ISBN 9780486152684.
- Wilson, Robin (2008), Lewis Carroll in Numberland: His fantastical mathematical logical life, an agony in eight fits, Penguin Books, hlm. 169–170, ISBN 978-0-14-101610-8, MR 2455534
- Yoshimura, Yoshimaru (July 1955), On the mechanism of buckling of a circular cylindrical shell under axial compression, Technical Memorandum 1390, National Advisory Committee for Aeronautics
- Young, Cynthia Y. (2011), Trigonometry, John Wiley & Sons, ISBN 9780470648025
Pranala luar
- (Inggris) Weisstein, Eric W., "Isosceles triangle", MathWorld


































