Heksagon: Perbedaan antara revisi
Bara Zeroun (bicara | kontrib) Tidak ada ringkasan suntingan Tag: VisualEditor Suntingan perangkat seluler Suntingan peramban seluler |
|||
| (16 revisi perantara oleh 8 pengguna tidak ditampilkan) | |||
| Baris 1: | Baris 1: | ||
{{Cleanup|reason=Messy|date=Agustus 2020}} |
|||
[[Berkas:HexagonConstructionAni.gif| |
[[Berkas:HexagonConstructionAni.gif|kiri|jmpl|Menggambar segienam beraturan dengan [[jangka]] dan [[mistar]]. Metode ini dituliskan oleh [[Euclides]] dalam ''[[Elements (Euclides)|Elements]]'', Buku IV, Proposisi 15.]] |
||
Dalam [[geometri]], ''' |
Dalam [[geometri]], '''Segi enam''' adalah sebuah segi banyak (''[[poligon]]'') dengan enam sisi dan enam titik sudut. Sebuah segienam beraturan memiliki [[simbol Schläfli]] {6}. |
||
{| border="1" bgcolor="#ffffff" cellpadding="5" align="right" style="margin-left:10px" width="250" |
{| border="1" bgcolor="#ffffff" cellpadding="5" align="right" style="margin-left:10px" width="250" |
||
!bgcolor=#e7dcc3 colspan=2|Segienam beraturan |
!bgcolor=#e7dcc3 colspan=2|Segienam beraturan |
||
|- |
|- |
||
|align=center colspan=2|[[Berkas: |
|align=center colspan=2|[[Berkas:Regular_polygon_6 annotated.svg|250px]]{{br}}Segienam beraturan, {6} |
||
|- |
|- |
||
|bgcolor=#e7dcc3|[[sisi]] dan [[titik sudut]]||6 |
|bgcolor=#e7dcc3|[[sisi]] dan [[titik sudut]]||6 |
||
| Baris 14: | Baris 15: | ||
|bgcolor=#e7dcc3|[[Grup simetri]]||[[Simetri dihedral|Dihedral]] (D<sub>6</sub>) |
|bgcolor=#e7dcc3|[[Grup simetri]]||[[Simetri dihedral|Dihedral]] (D<sub>6</sub>) |
||
|- |
|- |
||
|bgcolor=#e7dcc3|[[Luas]]{{br}}(''s''=panjang sisi)||<math> |
|bgcolor=#e7dcc3|[[Luas]]{{br}}(''s''=panjang sisi)||<math>L = \frac{3s^2}{2}\cot \frac{\pi}{6} = \frac{3 \sqrt{3}}{2}s^2</math>{{br}}<math> \simeq 2.598076211 s^2.</math> |
||
|- |
|- |
||
|bgcolor=#e7dcc3|[[Sudut |
|bgcolor=#e7dcc3|[[Sudut dalam]]||120° |
||
|} |
|} |
||
== Kontruksi == |
|||
[[Berkas:Hexagon Reguler Tertulis di Circle.gif|thumb|Kontruksi pada heksagon]] |
|||
[[Berkas:HexagonConstructionAni.gif|kiri|jmpl|Menggambar segienam beraturan dengan [[jangka]] dan [[mistar]]. Metode ini dituliskan oleh [[Euclides]] dalam ''[[Elements (Euclides)|Elements]]'', Buku IV, Proposisi 15.]] |
|||
== Segienam beraturan == |
== Segienam beraturan == |
||
| Baris 32: | Baris 37: | ||
Berkas:Honey_comb.jpg|Sarang [[lebah madu]] |
Berkas:Honey_comb.jpg|Sarang [[lebah madu]] |
||
Berkas:Carapax.svg|''[[Scutum]]'' dari [[karapas]] [[kura-kura]] |
Berkas:Carapax.svg|''[[Scutum]]'' dari [[karapas]] [[kura-kura]] |
||
Berkas:Saturn_hexagonal_north_pole_feature.jpg|Awan kutub utara di [[Saturnus]], ditemukan oleh [[Voyager 1]] dan [[Cassini-Huygens|Cassini]] [http://www.nasa.gov/mission_pages/cassini/multimedia/pia09188.html] [http://www.nasa.gov/mission_pages/cassini/media/cassini-20070327.html] |
Berkas:Saturn_hexagonal_north_pole_feature.jpg|Awan kutub utara di [[Saturnus]], ditemukan oleh [[Voyager 1]] dan [[Cassini-Huygens|Cassini]] [http://www.nasa.gov/mission_pages/cassini/multimedia/pia09188.html] {{Webarchive|url=https://web.archive.org/web/20100216182237/http://www.nasa.gov/mission_pages/cassini/multimedia/pia09188.html |date=2010-02-16 }} [http://www.nasa.gov/mission_pages/cassini/media/cassini-20070327.html] {{Webarchive|url=https://web.archive.org/web/20100927072602/http://www.nasa.gov/mission_pages/cassini/media/cassini-20070327.html |date=2010-09-27 }} |
||
[http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1988Icar...76..335G&db_key=AST&data_type=HTML&format=] |
|||
Berkas:Hexa-peri-hexabenzocoronene ChemEurJ 2000 1834 commons.jpg|Struktur kristal dari ''[[koronen]]'' yang terbentuk dari cincin [[aromatis]] heksagonal, ditemukan oleh Müllen dkk., Chem. Eur. J., 2000, 1834-1839. |
Berkas:Hexa-peri-hexabenzocoronene ChemEurJ 2000 1834 commons.jpg|Struktur kristal dari ''[[koronen]]'' yang terbentuk dari cincin [[aromatis]] heksagonal, ditemukan oleh Müllen dkk., Chem. Eur. J., 2000, 1834-1839. |
||
Berkas:Giants causeway closeup.jpg|Kolom [[basal]] alami di ''[[Giant's Causeway]]'', [[Irlandia]] |
Berkas:Giants causeway closeup.jpg|Kolom [[basal]] alami di ''[[Giant's Causeway]]'', [[Irlandia]] |
||
Berkas:Fort-Jefferson Dry-Tortugas.jpg|Gambar udara dari [[Fort Jefferson]] di [[Dry Tortugas National Park|Taman Nasional Dry Tortugas]], [[Amerika Serikat]] |
Berkas:Fort-Jefferson Dry-Tortugas.jpg|Gambar udara dari [[Fort Jefferson]] di [[Dry Tortugas National Park|Taman Nasional Dry Tortugas]], [[Amerika Serikat]] |
||
Berkas:Jwst front view.jpg|Cermin dari [[Teleskop Webb]] dibuat dari 18 potongan segienam. |
Berkas:Jwst front view.jpg|Cermin dari [[Teleskop Webb]] dibuat dari 18 potongan segienam. |
||
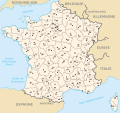
Berkas:Départements de France.svg| Negara [[ |
Berkas:Départements de France.svg| Negara [[Prancis]] berbentuk mirip segienam, sehingga kadang-kadang disebut "L'hexagone" (sang segienam). |
||
Berkas:Hexagon War.jpg|[[Hexagon War]], acara kuis di [[Trans7]] dengan arena segienam. |
Berkas:Hexagon War.jpg|[[Hexagon War]], acara kuis di [[Trans7]] dengan arena segienam. |
||
</gallery> |
</gallery> |
||
| Baris 44: | Baris 48: | ||
== Pranala luar == |
== Pranala luar == |
||
* {{MathWorld|title=Hexagon|urlname=Hexagon}} |
* {{MathWorld|title=Hexagon|urlname=Hexagon}} |
||
* [http://www.mathopenref.com/hexagon.html Definition and properties of a hexagon] With interactive animation |
* [http://www.mathopenref.com/hexagon.html Definition and properties of a hexagon] {{Webarchive|url=https://web.archive.org/web/20160220052134/http://www.mathopenref.com/hexagon.html |date=2016-02-20 }} With interactive animation |
||
* [http://www.nasa.gov/mission_pages/cassini/media/cassini-20070327.html Cassini Images Bizarre Hexagon on Saturn] |
* [http://www.nasa.gov/mission_pages/cassini/media/cassini-20070327.html Cassini Images Bizarre Hexagon on Saturn] {{Webarchive|url=https://web.archive.org/web/20100927072602/http://www.nasa.gov/mission_pages/cassini/media/cassini-20070327.html |date=2010-09-27 }} |
||
* [http://www.nasa.gov/mission_pages/cassini/multimedia/pia09188.html Saturn's Strange Hexagon] |
* [http://www.nasa.gov/mission_pages/cassini/multimedia/pia09188.html Saturn's Strange Hexagon] {{Webarchive|url=https://web.archive.org/web/20100216182237/http://www.nasa.gov/mission_pages/cassini/multimedia/pia09188.html |date=2010-02-16 }} |
||
* [http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1988Icar...76..335G&db_key=AST&data_type=HTML&format= A hexagonal feature around Saturn's North Pole] |
* [http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1988Icar...76..335G&db_key=AST&data_type=HTML&format= A hexagonal feature around Saturn's North Pole] {{Webarchive|url=https://web.archive.org/web/20170809033803/http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1988Icar...76..335G&db_key=AST&data_type=HTML&format= |date=2017-08-09 }} |
||
* [http://space.com/scienceastronomy/070327_saturn_hex.html "Bizarre Hexagon Spotted on Saturn"] - from [[Space.com]] (27 March 2007) |
* [http://space.com/scienceastronomy/070327_saturn_hex.html "Bizarre Hexagon Spotted on Saturn"] {{Webarchive|url=https://web.archive.org/web/20101224035625/http://www.space.com/scienceastronomy/070327_saturn_hex.html |date=2010-12-24 }} - from [[Space.com]] (27 March 2007) |
||
{{Poligon}} |
{{Poligon}} |
||
{{Authority control}} |
|||
[[Kategori:Poligon]] |
[[Kategori:Poligon]] |
||
Revisi per 22 Februari 2024 13.13
artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Masalah khususnya adalah: Messy |

Dalam geometri, Segi enam adalah sebuah segi banyak (poligon) dengan enam sisi dan enam titik sudut. Sebuah segienam beraturan memiliki simbol Schläfli {6}.
| Segienam beraturan | |
|---|---|
 Segienam beraturan, {6} | |
| sisi dan titik sudut | 6 |
| Simbol Schläfli | {6} t{3} |
| Diagram Coxeter–Dynkin | |
| Grup simetri | Dihedral (D6) |
| Luas (s=panjang sisi) |
|
| Sudut dalam | 120° |
Kontruksi

Segienam beraturan
Suatu segienam beraturan adalah suatu segienam dengan panjang sisi dan besar sudut dalam yang sama. Sudut dalam pada segienam beraturan adalah 120°. Segienam beraturan memiliki 6 simetri garis dan 6 simetri putar. Diagonal terpanjang dari segienam beraturan, yang menghubungkan dua titik sudut berseberangan, panjangnya adalah dua kali panjang satu sisinya. Jadi, segienam beraturan ini dapat dibagi menjadi enam segitiga sama sisi.
Sejumlah segienam dapat disusun bersama-sama dengan cara mempertemukan tiga segienam pada masing-masing salah satu sudutnya. Susunan ini digunakan lebah madu untuk membuat sarangnya, karena susunan segienam merupakan bentuk yang paling efisien dari segi ruang dan bahan bangunan.
Luas dari sebuah segienam beraturan dengan panjang sisi s dihitung dengan rumus , sedangkan kelilingnya , diameter besar , dan diameter kecil .
Segienam di alam dan buatan manusia
-
Sarang lebah madu
-
Awan kutub utara di Saturnus, ditemukan oleh Voyager 1 dan Cassini [1] Diarsipkan 2010-02-16 di Wayback Machine. [2] Diarsipkan 2010-09-27 di Wayback Machine.
-
Cermin dari Teleskop Webb dibuat dari 18 potongan segienam.
-
Negara Prancis berbentuk mirip segienam, sehingga kadang-kadang disebut "L'hexagone" (sang segienam).
-
Hexagon War, acara kuis di Trans7 dengan arena segienam.
Pranala luar
- (Inggris) Weisstein, Eric W. "Hexagon". MathWorld.
- Definition and properties of a hexagon Diarsipkan 2016-02-20 di Wayback Machine. With interactive animation
- Cassini Images Bizarre Hexagon on Saturn Diarsipkan 2010-09-27 di Wayback Machine.
- Saturn's Strange Hexagon Diarsipkan 2010-02-16 di Wayback Machine.
- A hexagonal feature around Saturn's North Pole Diarsipkan 2017-08-09 di Wayback Machine.
- "Bizarre Hexagon Spotted on Saturn" Diarsipkan 2010-12-24 di Wayback Machine. - from Space.com (27 March 2007)









![Awan kutub utara di Saturnus, ditemukan oleh Voyager 1 dan Cassini [1] Diarsipkan 2010-02-16 di Wayback Machine. [2] Diarsipkan 2010-09-27 di Wayback Machine.](http://upload.wikimedia.org/wikipedia/commons/thumb/3/3e/Saturn_hexagonal_north_pole_feature.jpg/120px-Saturn_hexagonal_north_pole_feature.jpg)