Ruang vektor: Perbedaan antara revisi

Konten dihapus Konten ditambahkan

Sebaris

Revisi terkini sejak 2 Juli 2024 20.33

Ruang vektor adalah struktur matematika yang dibentuk oleh sekumpulan vektor, yaitu objek yang dapat dijumlahkan dan dikalikan dengan suatu bilangan, yang dinamakan skalar. Skalar sering adalah bilangan riil, tetapi kita juga dapat merumuskan ruang vektor dengan perkalian skalar dengan bilangan kompleks, bilangan rasional, atau bahkan medan. Operasi penjumlahan dan perkalian vektor mesti memenuhi persyaratan tertentu yang dinamakan aksioma. Contoh ruang vektor adalah vektor Euklides yang sering digunakan untuk melambangkan besaran fisika seperti gaya. Dua gaya dengan jenis sama dapat dijumlahkan untuk menghasilkan gaya ketiga, dan perkalian vektor gaya dengan bilangan riil adalah vektor gaya lain. Vektor yang melambangkan perpindahan pada bidang atau pada ruang tiga dimensi juga membentuk ruang vektor.

Ruang vektor merupakan subjek dari aljabar linear, dan dipahami dengan baik dari sudut pandang ini, karena ruang vektor dicirikan oleh dimensinya, yang menspesifikasikan banyaknya arah independen dalam ruang. Teori ruang vektor juga ditingkatkan dengan memperkenalkan struktur tambahan, seperti norma atau hasilkali dalam. Ruang seperti ini muncul dengan alamiah dalam analisis matematika, dalam bentuk ruang fungsi berdimensi takhingga, dengan vektornya adalah fungsi.

Secara historis, gagasan awal yang berbuah pada konsep ruang vektor dapat dilacak dari geometri analitik abad ke-17, matriks, sistem persamaan linear, dan vektor Euklides. Pembahasan modern yang lebih abstrak pertama kali dirumuskan oleh Giuseppe Peano pada akhir abad ke-19, yang meliput objek lebih umum daripada ruang Euklides, namun kebanyakan teori tersebut dapat dipandang sebagai perluasan gagasan geometri klasik seperti garis, bidang, dan analognya yang berdimensi lebih tinggi.

Saat ini, ruang vektor diterapkan di seluruh bidang matematika, sains dan rekayasa. Ruang vektor adalah konsep aljabar linear yang sesuai untuk menghadapi sistem persamaan linear, menawarkan kerangka kerja untuk deret Fourier (yang digunakan dalam pemampatan citra), atau menyediakan lingkungan yang dapat digunakan untuk teknik solusi persamaan diferensial parsial. Lebih jauh lagi, ruang vektor memberikan cara abstrak dan bebas koordinat untuk berurusan dengan objek geometris dan fisis seperti tensor. Pada gilirannya ini memungkinkan pemeriksaan sifat lokal manifold menggunakan teknik pelinearan. Ruang vektor dapat dirampatkan ke beberapa arah, dan menghasilkan konsep lebih lanjut dalam geometri dan aljabar abstrak.

Pendahuluan dan definisi

Konsep ruang vektor pertama-tama akan dijelaskan dengan menjelaskan dua contoh khusus:

Contoh pertama: panah suatu bidang

Contoh pertama ruang vektor terdiri dari panah dalam bidang tetap, dimulai dari satu titik tetap. Ini digunakan dalam fisika untuk menjelaskan gaya s atau kecepatan. Diberikan dua panah seperti, $v$ dan $w$ , jajaran genjang yang direntang oleh dua panah ini berisi satu panah diagonal yang juga dimulai dari titik awal. Panah baru ini disebut jumlah dari dua panah, dan dilambangkan $v + w$ .^[1] Dalam kasus khusus dari dua anak panah pada garis yang sama, jumlahnya adalah panah pada garis ini yang panjangnya adalah jumlah atau perbedaan panjangnya, tergantung pada apakah panah tersebut memiliki arah yang sama. Operasi lain yang dapat dilakukan dengan panah adalah penskalaan: diberikan bilangan riil $a$ positif, panah yang searah dengan $v$ , tetapi dilatasi atau dikecilkan dengan mengalikan panjangnya dengan $a$ , disebut perkalian dari $v$ dengan $a$ . Itu dilambangkan $a v$ . Jika $a$ negatif, $a v$ didefinisikan sebagai panah yang menunjuk ke arah yang berlawanan.

Berikut ini adalah beberapa contoh: jika $a = 2$ , vektor yang dihasilkan $a w$ memiliki arah yang sama dengan $w$ , tetapi direntangkan menjadi dua kali lipat panjang $w$ (gambar kanan bawah). Sama halnya, $2 w$ adalah jumlah $w + w$ . Bahkan, $(-1) v = - v$ memiliki arah berlawanan dan panjang yang sama $v$ (vektor biru menunjuk ke bawah pada gambar kanan).

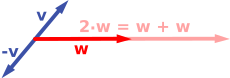
Contoh kedua: pasangan angka yang diurutkan

Contoh kunci kedua dari ruang vektor disediakan oleh pasangan bilangan riil $x$ dan $y$ . (Urutan komponen $x$ dan $y$ signifikan, sehingga pasangan seperti itu juga disebut pasangan terurut.) Pasangan seperti itu ditulis sebagai $(x, y)$ . Penjumlahan dari dua pasangan tersebut dan perkalian pasangan dengan bilangan didefinisikan sebagai berikut:

$(x_{1},y_{1})+(x_{2},y_{2})=(x_{1}+x_{2},y_{1}+y_{2})$

dan

$a(x,y)=(ax,ay)$ .

Contoh pertama di atas berkurang menjadi yang satu ini, jika panah diwakili oleh pasangan koordinat Kartesius dari titik ujungnya.

Definisi

Dalam artikel ini, vektor direpresentasikan dengan huruf tebal untuk membedakannya dari skalar.^{[nb 1]}

Sebuah ruang vektor di atas bidang $F$ adalah himpunan $V$ bersama dengan dua operasi yang memenuhi delapan aksioma tercantum di bawah ini. Berikut ini, $V \times V$ menunjukkan produk Cartesian dari $V$ dengan dirinya sendiri, dan $\to$ menunjukkan pemetaan dari satu himpunan ke himpunan lainnya.

Elemen $V$ biasanya disebut vektor . Elemen $F$ biasanya disebut skalar . Simbol umum untuk menunjukkan ruang vektor termasuk $U$ , $V$ dan $W$ .^[1]

Dalam dua contoh di atas, bidang adalah bidang dari bilangan real, dan himpunan vektor terdiri dari panah planar dengan titik awal tetap dan pasangan bilangan real.

Untuk memenuhi syarat sebagai ruang vektor, himpunan $V$ dan operasi penjumlahan dan perkalian harus mematuhi sejumlah persyaratan yang disebut aksioma.^[2] Ini tercantum dalam tabel di bawah ini, di mana $u$ , $v$ dan $w$ menunjukkan vektor arbitrer di $V$ , dan $a$ dan $b$ menunjukkan skalar di $F$ .^[3]^[4]

Aksioma	Rumus
Asosiatif tambahan	$u + (v + w) = (u + v) + w$
Komutatif tambahan	$u + v = v + u$
Elemen identitas penambahan	Ada elemen $0 \in V$ , disebut vektor nol , sepertiv $v + 0 = v$ untuk $v \in V$ .
Elemen invers penambahan	Untuk setiap $v \in V$ , ada elemen $- v \in V$ , disebut aditif invers dari $v$ , seperti yang $v + (- v) = 0$ .
Kompatibilitas dari perkalian skalar dengan perkalian bidang	$a (b v) = (ab) v$ ^{[nb 2]}
Elemen identitas perkalian skalar	$1 v = v$ , dengan $1$ menunjukkan multiplicative identity di $F$ .
Distributivitas perkalian skalar sehubungan dengan penambahan vektor	$a (u + v) = a u + a v$
Distributivitas perkalian skalar sehubungan dengan penambahan medan	$(a + b) v = a v + b v$

Aksioma ini menggeneralisasi properti vektor yang diperkenalkan pada contoh di atas. Memang, hasil penjumlahan dua pasangan berurutan (seperti contoh kedua di atas) tidak bergantung pada urutan penjumlahan:

(x v, y v) + (x w, y w) = (x w, y w) + (x v, y v)

.

Demikian juga, dalam contoh geometris vektor sebagai panah, $v + w = w + v$ karena jajar genjang yang menentukan jumlah vektor tidak bergantung pada urutan vektor. Semua aksioma lainnya dapat diverifikasi dengan cara yang sama pada kedua contoh. Jadi, dengan mengabaikan sifat konkret dari jenis vektor tertentu, definisi menggabungkan dua dan lebih banyak contoh dalam satu pengertian ruang vektor.

Pengurangan dua vektor dan pembagian dengan skalar (bukan nol) dapat didefinisikan sebagai

{\begin{aligned}\mathbf {v} -\mathbf {w} &=\mathbf {v} +(-\mathbf {w} )\\{\frac {\mathbf {v} }{a}}&={\frac {1}{a}}\mathbf {v} \end{aligned}}

.

Ketika bidang skalar $F$ adalah bilangan real $R$ , ruang vektor disebut ruang vektor nyata . Jika bidang skalar adalah bilangan kompleks $C$ , ruang vektor disebut ruang vektor kompleks . Kedua kasus ini adalah yang paling sering digunakan dalam bidang teknik. Definisi umum ruang vektor memungkinkan skalar menjadi elemen dari setiap bidang $F$ tetap. Gagasan tersebut kemudian dikenal sebagai $F$ - ruang vektor atau ruang vektor di atas $F$ . Bidang pada dasarnya adalah sekumpulan angka yang memiliki operasi penambahan, pengurangan, perkalian dan pembagian.^{[nb 3]} Misalnya, bilangan rasional membentuk suatu bidang.

Berbeda dengan intuisi yang berasal dari vektor pada bidang dan kasus berdimensi lebih tinggi, dalam ruang vektor umum, tidak ada gagasan tentang kedekatan, sudut atau jarak. Untuk menangani hal-hal tersebut, jenis ruang vektor tertentu diperkenalkan; lihat Ruang vektor dengan struktur tambahan di bawah untuk informasi selengkapnya.

Rumus alternatif dan konsekuensi dasar

Penjumlahan vektor dan perkalian skalar adalah operasi, memenuhi sifat penutupan: $u + v$ dan $a v$ berada di $V$ untuk $a$ pada $F$ , dan $u$ , $v$ ke $V$ . Beberapa sumber yang lebih tua menyebutkan sifat-sifat ini sebagai aksioma yang terpisah.^[5]

Dalam bahasa aljabar abstrak, empat aksioma pertama ekivalen dengan mensyaratkan himpunan vektor menjadi grup Abelian di bawah tambahan. Aksioma yang tersisa memberi grup ini struktur $F$ -modul. Dengan kata lain, ada ring homomorphism $f$ dari bidang $F$ ke dalam gelanggang endomorfisme dari grup vektor. Kemudian perkalian skalar $a v$ didefinisikan sebagai $(f (a))(v)$ .^[6]

Sejarah

Ruang vektor berasal dari geometri affine, melalui pengenalan koordinat pada bidang atau ruang tiga dimensi. Sekitar 1636, ahli matematika Prancis René Descartes dan Pierre de Fermat mendirikan geometri analitik dengan mengidentifikasi solusi persamaan dua variabel dengan titik-titik pada bidang kurva.^[7] Untuk mencapai solusi geometris tanpa menggunakan koordinat, Bolzano diperkenalkan, pada tahun 1804, operasi tertentu pada titik, garis dan bidang, yang merupakan pendahulu vektor.^[8] This work was made use of in the conception of barycentric coordinates by Möbius in 1827.^[9] Landasan dari definisi vektor adalah Bellavitis 'pengertian bipoint, segmen berorientasi salah satu ujungnya adalah asal dan yang lain target. Vektor dipertimbangkan kembali dengan penyajian bilangan kompleks oleh Argand dan Hamilton dan dimulainya Kuarternion oleh yang terakhir.^[10] Mereka adalah elemen dalam R² dan R⁴; memperlakukan mereka menggunakan kombinasi linier s kembali ke Laguerre pada tahun 1867, yang juga mendefinisikan sistem persamaan linear.

Pada tahun 1857, Cayley memperkenalkan notasi matriks yang memungkinkan harmonisasi dan penyederhanaan peta linear. Sekitar waktu yang sama, Grassmann mempelajari kalkulus barycentric yang diprakarsai oleh Mbius. Dia membayangkan kumpulan objek abstrak yang diberkahi dengan operasi.^[11] Dalam karyanya, konsep kebebasan linear dan dimensi, serta produk skalar hadir. Sebenarnya karya Grassmann tahun 1844 melebihi kerangka vektor ruang, karena perkaliannya yang mempertimbangkan, juga, membawanya ke apa yang sekarang disebut aljabar. Matematikawan Italia Peano adalah orang pertama yang memberikan definisi modern ruang vektor dan peta linier pada tahun 1888.^[12]

Perkembangan penting dari ruang vektor adalah karena pembangunan ruang fungsi oleh Henri Lebesgue. Ini kemudian diresmikan oleh Banach dan Hilbert, sekitar 1920.^[13] Pada saat itu, aljabar dan bidang baru analisis fungsional mulai berinteraksi, terutama dengan konsep-konsep kunci seperti Ruang L^p dan ruang Hilbert.^[14] Juga pada saat ini, studi pertama tentang ruang vektor berdimensi tak hingga telah dilakukan.

Contoh

Ruang koordinat

Contoh paling sederhana dari ruang vektor di atas bidang $F$ adalah bidang itu sendiri, dilengkapi dengan penjumlahan dan perkalian standarnya. Lebih umum lagi, semua $n$ -tupel (urutan panjang $n$ )

(a 1, a 2, ..., a n)

dari elemen $F$ membentuk ruang vektor yang biasanya dilambangkan $F n$ dan disebut ruang koordinat.^[15] Kasus $n = 1$ adalah contoh paling sederhana yang disebutkan di atas, di mana bidang $F$ juga dianggap sebagai ruang vektor di atasnya. Kasus $F = R$ and $n = 2$ telah dibahas dalam pendahuluan di atas.

Bilangan kompleks dan ekstensi bidang lainnya

Himpunan bilangan kompleks $C$ , Artinya, angka yang bisa dituliskan dalam bentuk $x + iy$ untuk bilangan real $x$ dan $y$ di mana $i$ adalah satuan imajiner , bentuk ruang vektor di atas real dengan penjumlahan dan perkalian seperti biasa: $(x + iy) + (a + ib) = (x + a) + i (y + b)$ dan $c \cdot (x + iy) = (c \cdot x) + i (c \cdot y)$ untuk bilangan real $x$ , $y$ , $a$ , $b$ dan $c$ . Berbagai aksioma ruang vektor mengikuti fakta bahwa aturan yang sama berlaku untuk aritmatika bilangan kompleks.

Faktanya, contoh bilangan kompleks pada dasarnya sama (yaitu isomorfik ) dengan ruang vektor pasangan terurut bilangan real yang disebutkan di atas: jika kita memikirkan bilangan kompleks $x + i y$ sebagai mewakili urutan $(x, y)$ di bidang kompleks kemudian kita melihat bahwa aturan penjumlahan dan perkalian skalar sama persis dengan yang ada di contoh sebelumnya.

Secara lebih umum, ekstensi bidang menyediakan kelas lain dari contoh ruang vektor, terutama dalam aljabar dan teori bilangan aljabar: bidang $F$ berisi bidang lebih kecil $E$ adalah ruang vektor- $E$ , dengan operasi perkalian dan penjumlahan yang diberikan $F$ .^[16] Misalnya, bilangan kompleks adalah ruang vektor $R$ , dan ekstensi bidang $\mathbf {Q} (i{\sqrt {5}})$ adalah vektor ruang atas $Q$ .

Ruang fungsi

Fungsi dari himpunan tetap $Ω$ ke bidang $F$ juga membentuk ruang vektor, dengan melakukan penjumlahan dan perkalian skalar searah jarum jam. Artinya, jumlah dari dua fungsi $f$ dan $g$ adalah fungsi $(f + g)$ diberikan oleh

(f + g)(w) = f (w) + g (w)

,

dan juga untuk perkalian. Ruang fungsi seperti itu terjadi dalam banyak situasi geometris, ketika $Ω$ adalah garis nyata atau interval, atau himpunan bagian lainnya dari $R$ . Banyak gagasan dalam topologi dan analisis, seperti kontinuitas, integrabilitas atau diferensiabilitas berperilaku baik sehubungan dengan linearitas: penjumlahan dan kelipatan skalar dari fungsi yang memiliki sifat seperti itu masih memiliki sifat itu.^[17] Oleh karena itu, himpunan fungsi tersebut adalah ruang vektor. Mereka dipelajari secara lebih rinci menggunakan metode analisis fungsional, lihat di bawah.^{[butuh klarifikasi]} Batasan aljabar juga menghasilkan ruang vektor: ruang vektor $F [x]$ diberikan oleh fungsi polinomial:

f (x) = r 0 + r 1 x + ... + r n -1 x n -1 + r n x n

, dimana koefisien

r 0, ..., r n

berada di

F

.^[18]

Persamaan linear

Sistem persamaan linear homogen s terkait erat dengan ruang vektor.^[19] For example, the solutions of

$a$	$+$	$3 b$	$+$	$c$	$= 0$
$4 a$	$+$	$2 b$	$+$	$2 c$	$= 0$

diberikan dengan tiga kali lipat dengan sembarang $a$ , $b = a /2$ , dan $c = -5 a /2$ . Mereka membentuk ruang vektor: penjumlahan dan kelipatan skalar dari tiga kali lipat masih memenuhi rasio yang sama dari ketiga variabel; jadi mereka juga solusi. Matriks dapat digunakan untuk memadatkan beberapa persamaan linier seperti di atas menjadi satu persamaan vektor, yaitu

A x = 0

,

dimana $A =$ ${\begin{bmatrix}1&3&1\\4&2&2\end{bmatrix}}$ is matriks yang berisi koefisien dari persamaan yang diberikan, $x$ adalah vektor $(a, b, c)$ , $A x$ menunjukkan produk matriks, dan $0 = (0, 0)$ adalah vektor nol. Dengan nada yang sama, solusi dari persamaan diferensial linier homogen membentuk ruang vektor. Sebagai contoh,

f''(x) + 2 f'(x) + f (x) = 0

hasil $f (x) = a e - x + bx e - x$ , dimana $a$ dan $b$ adalah konstanta arbitrer, dan $e x$ adalah fungsi eksponensial alami.

Definisi formal

Sebuah ruang vektor (atas medan F) adalah himpunan V, bersama-sama dengan dua operasi, yaitu penjumlahan vektor dan perkalian skalar, dan memenuhi aksioma-aksioma berikut (untuk semua $\mathbf {u} ,\mathbf {v} ,\mathbf {w} \in V$ dan $a,b\in F$ ):

Aksioma	Pernyataan
Sifat asosiatif penjumlahan	u + (v + w) = (u + v) + w.
Sifat komutatif penjumlahan	v + w = w + v.
Elemen identitas penjumlahan	Terdapat elemen 0 ∈ V, dinamakan sebagai vektor nol, sedemikian sehingga v + 0 = v untuk semua v ∈ V.
Elemen invers penjumlahan	Untuk semua v ∈ V, terdapat elemen w ∈ V, dinamakan sebagai invers penjumlahan v, sedemikan sehingga v + w = 0. Invers penjumlahan ini dilambangkan sebagai −v.
Sifat distributif perkalian skalar terhadap penjumlahan vektor	a(v + w) = av + aw.
Sifat distributif perkalian skalar terhadap penjumlahan medan	(a + b)v = av + bv.
Kesesuaian perkalian skalar dengan perkalian medan	a(bv) = (ab)v ^[20]
Elemen identitas pada perkalian skalar	1v = v, dengan 1 melambangkan entitas perkalian dalam F.

Dalam peta linear

Kasus khusus yang penting adalah ketika $V = W$ , di mana peta linearnya disebut endomorfisme (linear) dari $V$ . Terkadang istilah operator linear dipakai untuk kasus ini.^[21] Dalam kebiasaan yang lain, operator linear membolehkan $V$ dan $W$ yang berbeda, tetapi mereka harus merupakan urang vektor real.^[22] Terkadang istilah fungsi linear memiliki arti yang sama dengan peta linear, sedangkan dalam geometri analisis artinya berbeda.

Sebuah peta linear selalu memetakan subruang linear ke subruang linear (mungkin dengan dimension yang lebih rendah);^[23] contohnya pemetaan sebuah bidang yang melalui titik nol ke sebuah bidang, garis lurus atau titik. Peta linear biasanya dilambangkan sebagai matriks, dan contoh sederhananya adalah transformasi linear rotasi dan pencerminan.

Dalam bahasa aljabar abstrak, sebuah peta linear merupakan sebuah homoformisme modul. Dalam bahasa teori kategori, sebuah peta linear merupakan sebuah morfisme dalam kategori modul pada sebuah gelanggang.

Lihat pula

Vektor (matematika dan fisika), untuk daftar berbagai macam vektor

Catatan

^ Ini juga umum, terutama dalam fisika, untuk menunjukkan vektor dengan panah di atasnya: $Templat:Vec$ .
^ Aksioma ini dan selanjutnya mengacu pada dua operasi yang berbeda: perkalian skalar: $b v$ ; dan perkalian lapangan: $ab$ . Mereka tidak menegaskan asosiatif dari kedua operasi tersebut. Secara lebih formal, perkalian skalar adalah aksi monoid dari perkalian monoid bidang $F$ pada ruang vektor $V$ .
^ Some authors (such as Brown 1991) batasi perhatian pada bidang $R$ atau $C$ , tetapi sebagian besar teori tidak berubah untuk bidang arbitrer.

Kutipan

^ ^a ^b "Comprehensive List of Algebra Symbols". Math Vault (dalam bahasa Inggris). 2020-03-25. Diakses tanggal 2020-08-23.
^ Roman 2005, ch. 1, p. 27
^ "5: Vector Spaces". Mathematics LibreTexts (dalam bahasa Inggris). 2016-02-29. Diakses tanggal 2020-08-23.
^ Weisstein, Eric W. "Vector Space". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2020-08-23.
^ van der Waerden 1993, Ch. 19
^ Bourbaki 1998, §II.1.1. Bourbaki menyebut grup homomorfisme $f (a)$ homotheties.
^ Bourbaki 1969, ch. "Algèbre linéaire et algèbre multilinéaire", pp. 78–91.
^ Bolzano 1804.
^ Möbius 1827.
^ Hamilton 1853.
^ Grassmann 2000.
^ Peano 1888, ch. IX.
^ Banach 1922.
^ Dorier 1995, Moore 1995.
^ Lang 1987, ch. I.1
^ Lang 2002, ch. V.1
^ Lang 1993, ch. XII.3., p. 335
^ Lang 1987, ch. IX.1
^ Lang 1987, ch. VI.3.
^ Aksioma ini tidak menyatakan sifat asosiatif operasi, karena ada dua operasi dalam hal ini, perkalian skalar: bv; dan perkalian medan: ab.
^ Transformasi linear dari $V$ ke $V$ sering disebut operator linear di $V$ Rudin 1976, hlm. 207
^ Misalkan $V$ dan $W$ adalah dua ruang vektor real. Sebuat pemetaan dari $V$ ke $W$ disebut sebuah 'pemetaan linear' atau 'transformasi linear' atau 'operator linear' [...] dari $V$ ke $W$ , apabila
${\textstyle a(u+v)=au+av}$ untuk setiap ${\textstyle u,v\in V}$ ,
${\textstyle a(\lambda u)=\lambda au}$ untuk setiap $u\in V$ dan semua $λ$ real. Bronshtein, Semendyayev 2004, hlm. 316
^
Rudin 1991, hlm. 14
Berikut beberapa sifat dari pemetaan linear ${\textstyle \Lambda :X\to Y}$ ${\textstyle \Lambda :X\to Y}$ yang buktinya sangat mudah jadi kita tidak menuliskannya; diasumsikan bahwa ${\textstyle A\subset X}$ ${\textstyle A\subset X}$ dan ${\textstyle B\subset Y}$ ${\textstyle B\subset Y}$ :
1. ${\textstyle \Lambda 0=0.}$
2. Jika $A$ merupakan sebuah subruang (atau sebuah himpunan konveks, atau sebuah himpunan seimbang) hal yang sama berlaku juga di ${\textstyle \Lambda (A)}$
3. Jika $B$ merupakan sebuah subruang (atau sebuah himpunan konveks, atau sebuah himpunan seimbang) hal yang sama berlaku juga di ${\textstyle \Lambda ^{-1}(B)}$
4. Secara khusus, himpunan:
  $\Lambda ^{-1}(\{0\})=\{x\in X:\Lambda x=0\}={N}(\Lambda )$
  merupakan sebuah subruang dari $X$ , disebut ruang nol dari ${\textstyle \Lambda }$ .

Referensi

Aljabar

Artin, Michael (1991), Algebra, Prentice Hall, ISBN 978-0-89871-510-1
Blass, Andreas (1984), "Existence of bases implies the axiom of choice", Axiomatic set theory (Boulder, Colorado, 1983), Contemporary Mathematics, 31, Providence, R.I.: American Mathematical Society, hlm. 31–33, MR 0763890
Brown, William A. (1991), Matrices and vector spaces, New York: M. Dekker, ISBN 978-0-8247-8419-5
Lang, Serge (1987), Linear algebra, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96412-6
Templat:Lang Algebra
Mac Lane, Saunders (1999), Algebra (edisi ke-3rd), hlm. 193–222, ISBN 978-0-8218-1646-2
Meyer, Carl D. (2000), Matrix Analysis and Applied Linear Algebra, SIAM, ISBN 978-0-89871-454-8
Roman, Steven (2005), Advanced Linear Algebra, Graduate Texts in Mathematics, 135 (edisi ke-2nd), Berlin, New York: Springer-Verlag, ISBN 978-0-387-24766-3
Spindler, Karlheinz (1993), Abstract Algebra with Applications: Volume 1: Vector spaces and groups, CRC, ISBN 978-0-8247-9144-5
van der Waerden, Bartel Leendert (1993), Algebra (dalam bahasa Jerman) (edisi ke-9th), Berlin, New York: Springer-Verlag, ISBN 978-3-540-56799-8

Analisis

Bourbaki, Nicolas (1987), Topological vector spaces, Elements of mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-13627-9
Bourbaki, Nicolas (2004), Integration I, Berlin, New York: Springer-Verlag, ISBN 978-3-540-41129-1
Braun, Martin (1993), Differential equations and their applications: an introduction to applied mathematics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-97894-9
BSE-3 (2001) [1994], "Tangent plane", dalam Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
Choquet, Gustave (1966), Topology, Boston, MA: Academic Press
Dennery, Philippe; Krzywicki, Andre (1996), Mathematics for Physicists, Courier Dover Publications, ISBN 978-0-486-69193-0
Dudley, Richard M. (1989), Real analysis and probability, The Wadsworth & Brooks/Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN 978-0-534-10050-6
Dunham, William (2005), The Calculus Gallery, Princeton University Press, ISBN 978-0-691-09565-3
Evans, Lawrence C. (1998), Partial differential equations, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0772-9
Folland, Gerald B. (1992), Fourier Analysis and Its Applications, Brooks-Cole, ISBN 978-0-534-17094-3
Gasquet, Claude; Witomski, Patrick (1999), Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets, Texts in Applied Mathematics, New York: Springer-Verlag, ISBN 978-0-387-98485-8
Ifeachor, Emmanuel C.; Jervis, Barrie W. (2001), Digital Signal Processing: A Practical Approach (edisi ke-2nd), Harlow, Essex, England: Prentice-Hall (dipublikasikan tanggal 2002), ISBN 978-0-201-59619-9
Krantz, Steven G. (1999), A Panorama of Harmonic Analysis, Carus Mathematical Monographs, Washington, DC: Mathematical Association of America, ISBN 978-0-88385-031-2
Kreyszig, Erwin (1988), Advanced Engineering Mathematics (edisi ke-6th), New York: John Wiley & Sons, ISBN 978-0-471-85824-9
Kreyszig, Erwin (1989), Introductory functional analysis with applications, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-50459-7, MR 0992618
Lang, Serge (1983), Real analysis, Addison-Wesley, ISBN 978-0-201-14179-5
Lang, Serge (1993), Real and functional analysis, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94001-4
Loomis, Lynn H. (1953), An introduction to abstract harmonic analysis, Toronto-New York–London: D. Van Nostrand Company, Inc., hlm. x+190, hdl:2027/uc1.b4250788 
Templat:Narici Beckenstein Topological Vector Spaces
Templat:Schaefer Wolff Topological Vector Spaces
Treves, François (1967), Topological vector spaces, distributions and kernels, Boston, MA: Academic Press

Referensi sejarah

Banach, Stefan (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)" (PDF), Fundamenta Mathematicae (dalam bahasa Prancis), 3: 133–181, doi:10.4064/fm-3-1-133-181, ISSN 0016-2736
Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) (dalam bahasa Jerman)
Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics) (dalam bahasa Prancis), Paris: Hermann
Dorier, Jean-Luc (1995), "A general outline of the genesis of vector space theory", Historia Mathematica, 22 (3): 227–261, doi:10.1006/hmat.1995.1024 , MR 1347828
Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (dalam bahasa Prancis), Chez Firmin Didot, père et fils
Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (dalam bahasa Jerman), O. Wigand , reprint: Grassmann, Hermann (2000), Kannenberg, L.C., ed., Extension Theory, diterjemahkan oleh Kannenberg, Lloyd C., Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2031-5
Hamilton, William Rowan (1853), Lectures on Quaternions, Royal Irish Academy
Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) (dalam bahasa Jerman), diarsipkan dari versi asli tanggal 2006-11-23
Moore, Gregory H. (1995), "The axiomatization of linear algebra: 1875–1940", Historia Mathematica, 22 (3): 262–303, doi:10.1006/hmat.1995.1025 
Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (dalam bahasa Italia), Turin
Peano, G. (1901) Formulario mathematico: vct axioms via Internet Archive

Referensi lebih lanjut

Ashcroft, Neil; Mermin, N. David (1976), Solid State Physics, Toronto: Thomson Learning, ISBN 978-0-03-083993-1
Atiyah, Michael Francis (1989), K-theory, Advanced Book Classics (edisi ke-2nd), Addison-Wesley, ISBN 978-0-201-09394-0, MR 1043170
Bourbaki, Nicolas (1998), Elements of Mathematics : Algebra I Chapters 1-3, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64243-5
Bourbaki, Nicolas (1989), General Topology. Chapters 1-4, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64241-1
Coxeter, Harold Scott MacDonald (1987), Projective Geometry (edisi ke-2nd), Berlin, New York: Springer-Verlag, ISBN 978-0-387-96532-1
Eisenberg, Murray; Guy, Robert (1979), "A proof of the hairy ball theorem", The American Mathematical Monthly, 86 (7): 572–574, doi:10.2307/2320587, JSTOR 2320587
Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics, 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94269-8, MR 1322960
Goldrei, Derek (1996), Classic Set Theory: A guided independent study (edisi ke-1st), London: Chapman and Hall, ISBN 978-0-412-60610-6
Griffiths, David J. (1995), Introduction to Quantum Mechanics, Upper Saddle River, NJ: Prentice Hall, ISBN 978-0-13-124405-4
Halmos, Paul R. (1974), Finite-dimensional vector spaces, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90093-3
Halpern, James D. (Jun 1966), "Bases in Vector Spaces and the Axiom of Choice", Proceedings of the American Mathematical Society, 17 (3): 670–673, doi:10.2307/2035388 , JSTOR 2035388
Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013), Calculus : Single and Multivariable (edisi ke-6), John Wiley & Sons, ISBN 978-0470-88861-2
Husemoller, Dale (1994), Fibre Bundles (edisi ke-3rd), Berlin, New York: Springer-Verlag, ISBN 978-0-387-94087-8
Jost, Jürgen (2005), Riemannian Geometry and Geometric Analysis (edisi ke-4th), Berlin, New York: Springer-Verlag, ISBN 978-3-540-25907-7
Kreyszig, Erwin (1991), Differential geometry, New York: Dover Publications, hlm. xiv+352, ISBN 978-0-486-66721-8
Kreyszig, Erwin (1999), Advanced Engineering Mathematics (edisi ke-8th), New York: John Wiley & Sons, ISBN 978-0-471-15496-9
Luenberger, David (1997), Optimization by vector space methods, New York: John Wiley & Sons, ISBN 978-0-471-18117-0
Mac Lane, Saunders (1998), Categories for the Working Mathematician (edisi ke-2nd), Berlin, New York: Springer-Verlag, ISBN 978-0-387-98403-2
Misner, Charles W.; Thorne, Kip; Wheeler, John Archibald (1973), Gravitation, W. H. Freeman, ISBN 978-0-7167-0344-0
Naber, Gregory L. (2003), The geometry of Minkowski spacetime, New York: Dover Publications, ISBN 978-0-486-43235-9, MR 2044239
Schönhage, A.; Strassen, Volker (1971), "Schnelle Multiplikation großer Zahlen (Fast multiplication of big numbers)", Computing (dalam bahasa Jerman), 7 (3–4): 281–292, doi:10.1007/bf02242355, ISSN 0010-485X
Spivak, Michael (1999), A Comprehensive Introduction to Differential Geometry (Volume Two), Houston, TX: Publish or Perish
Stewart, Ian (1975), Galois Theory, Chapman and Hall Mathematics Series, London: Chapman and Hall, ISBN 978-0-412-10800-6
Varadarajan, V. S. (1974), Lie groups, Lie algebras, and their representations, Prentice Hall, ISBN 978-0-13-535732-3
Wallace, G.K. (Feb 1992), "The JPEG still picture compression standard" (PDF), IEEE Transactions on Consumer Electronics, 38 (1): xviii–xxxiv, CiteSeerX 10.1.1.318.4292 , doi:10.1109/30.125072, ISSN 0098-3063, diarsipkan dari versi asli (PDF) tanggal 2007-01-13, diakses tanggal 2017-10-25
Templat:Weibel IHA

Pranala luar

Hazewinkel, Michiel, ed. (2001) [1994], "Vector space", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4

[2] Ini juga umum, terutama dalam fisika, untuk menunjukkan vektor dengan panah di atasnya: $Templat:Vec$ .

[6] Aksioma ini dan selanjutnya mengacu pada dua operasi yang berbeda: perkalian skalar: $b v$ ; dan perkalian lapangan: $ab$ . Mereka tidak menegaskan asosiatif dari kedua operasi tersebut. Secara lebih formal, perkalian skalar adalah aksi monoid dari perkalian monoid bidang $F$ pada ruang vektor $V$ .

[7] Some authors (such as Brown 1991) batasi perhatian pada bidang $R$ atau $C$ , tetapi sebagian besar teori tidak berubah untuk bidang arbitrer.

[:0-1] "Comprehensive List of Algebra Symbols". Math Vault (dalam bahasa Inggris). 2020-03-25. Diakses tanggal 2020-08-23.

[3] Roman 2005, ch. 1, p. 27

[4] "5: Vector Spaces". Mathematics LibreTexts (dalam bahasa Inggris). 2016-02-29. Diakses tanggal 2020-08-23.

[5] Weisstein, Eric W. "Vector Space". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2020-08-23.

[8] van der Waerden 1993, Ch. 19

[9] Bourbaki 1998, §II.1.1. Bourbaki menyebut grup homomorfisme $f (a)$ homotheties.

[10] Bourbaki 1969, ch. "Algèbre linéaire et algèbre multilinéaire", pp. 78–91.

[11] Bolzano 1804.

[12] Möbius 1827.

[13] Hamilton 1853.

[14] Grassmann 2000.

[15] Peano 1888, ch. IX.

[16] Banach 1922.

[17] Dorier 1995, Moore 1995.

[18] Lang 1987, ch. I.1

[19] Lang 2002, ch. V.1

[20] Lang 1993, ch. XII.3., p. 335

[21] Lang 1987, ch. IX.1

[22] Lang 1987, ch. VI.3.

[nb-23] Aksioma ini tidak menyatakan sifat asosiatif operasi, karena ada dua operasi dalam hal ini, perkalian skalar: bv; dan perkalian medan: ab.

[24] Transformasi linear dari $V$ ke $V$ sering disebut operator linear di $V$ Rudin 1976, hlm. 207

[25] Misalkan $V$ dan $W$ adalah dua ruang vektor real. Sebuat pemetaan dari $V$ ke $W$ disebut sebuah 'pemetaan linear' atau 'transformasi linear' atau 'operator linear' [...] dari $V$ ke $W$ , apabila
${\textstyle a(u+v)=au+av}$ untuk setiap ${\textstyle u,v\in V}$ ,
${\textstyle a(\lambda u)=\lambda au}$ untuk setiap $u\in V$ dan semua $λ$ real. Bronshtein, Semendyayev 2004, hlm. 316

[26] Rudin 1991, hlm. 14
Berikut beberapa sifat dari pemetaan linear ${\textstyle \Lambda :X\to Y}$ yang buktinya sangat mudah jadi kita tidak menuliskannya; diasumsikan bahwa ${\textstyle A\subset X}$ dan ${\textstyle B\subset Y}$ :
${\textstyle \Lambda 0=0.}$
Jika $A$ merupakan sebuah subruang (atau sebuah himpunan konveks, atau sebuah himpunan seimbang) hal yang sama berlaku juga di ${\textstyle \Lambda (A)}$
Jika $B$ merupakan sebuah subruang (atau sebuah himpunan konveks, atau sebuah himpunan seimbang) hal yang sama berlaku juga di ${\textstyle \Lambda ^{-1}(B)}$
Secara khusus, himpunan:
$\Lambda ^{-1}(\{0\})=\{x\in X:\Lambda x=0\}={N}(\Lambda )$
merupakan sebuah subruang dari $X$ , disebut ruang nol dari ${\textstyle \Lambda }$ .

[27] ${\textstyle \Lambda 0=0.}$

[28] Jika $A$ merupakan sebuah subruang (atau sebuah himpunan konveks, atau sebuah himpunan seimbang) hal yang sama berlaku juga di ${\textstyle \Lambda (A)}$

[29] Jika $B$ merupakan sebuah subruang (atau sebuah himpunan konveks, atau sebuah himpunan seimbang) hal yang sama berlaku juga di ${\textstyle \Lambda ^{-1}(B)}$

[30] Secara khusus, himpunan:
$\Lambda ^{-1}(\{0\})=\{x\in X:\Lambda x=0\}={N}(\Lambda )$
merupakan sebuah subruang dari $X$ , disebut ruang nol dari ${\textstyle \Lambda }$ .

[31] ${\textstyle \Lambda 0=0.}$

[32] Jika $A$ merupakan sebuah subruang (atau sebuah himpunan konveks, atau sebuah himpunan seimbang) hal yang sama berlaku juga di ${\textstyle \Lambda (A)}$

[33] Jika $B$ merupakan sebuah subruang (atau sebuah himpunan konveks, atau sebuah himpunan seimbang) hal yang sama berlaku juga di ${\textstyle \Lambda ^{-1}(B)}$

[34] Secara khusus, himpunan:
$\Lambda ^{-1}(\{0\})=\{x\in X:\Lambda x=0\}={N}(\Lambda )$
merupakan sebuah subruang dari $X$ , disebut ruang nol dari ${\textstyle \Lambda }$ .

[1]

[nb 1]

[2]

[3]

[4]

[nb 2]

[nb 3]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

l b s Aljabar linear
Konsep dasar	Skalar Vektor Ruang vektor Perkalian skalar Proyeksi vektor Rentang linear Peta linear Proyeksi linear Kebebasan linear Kombinasi linear Basis Vektor kolom dan baris Ruang kolom dan baris Keortogonalan Kernel Nilai eigen dan vektor eigen Hasil kali luar Ruang hasil kali dalam Hasil kali titik Transpos Proses Gram–Schmidt Persamaan linear
Aljabar vektor	Hasil kali silang Hasil kali tripel Hasil kali silang tujuh dimensi
Aljabar multilinear	Aljabar geometri Aljabar eksterior Bivektor Multivektor Tensor Morfisme luar
Matriks	Blok Penguraian Dapat dibalik Minor Perkalian Rank Transformasi Aturan Cramer Eliminasi Gauss Determinan
Konstruksi aljabar	Dual Hasil kali tensor Jumlah langsung Kuosien Ruang fungsi Subruang
Numerik	Floating-point Stabilitas numerik Basic Linear Algebra Subprograms (BLAS) Matriks rongga Perbandingan pustaka aljabar linear Perbandingan perangkat lunak analisis numerik
Kategori Garis besar Portal matematika Wikibuku