Kekisi (tatanan)
| Relasi biner | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Simbol "✓" menunjukkan bahwa sifat kolom diperlukan dalam definisi baris. Misalnya, definisi relasi ekuivalen diperlukan menjadi simetris. Semua definisi secara diam-diam memerlukan ketransitifan dan refleksivitas. |
| Struktur aljabar |
|---|
Kisi adalah struktur abstrak digunakan dalam subdisiplin matematika dari teori order dan aljabar abstrak. Himpunan terurut sebagian di mana dua elemen memiliki supremum (juga disebut batas atas terkecil atau gabung) dan infimum (juga disebut batas bawah terbesar atau bertemu). Contoh dari bilangan asli, dengan diurutkan oleh pembagian, dimana supremum adalah kelipatan persekutuan terkecil dan infimum adalah pembagi persekutuan terbesar.
Kisi dikarakterisasi sebagai struktur aljabar menggunakan aksioma atik identitas. Karena kedua definisi tersebut ekuivalen, teori kisi yang menggunakan teori urutan dan aljabar universal. Semikisi salah satu bagian kisi adalah aljabar Heyting dan Boolean. Struktur "kisi" digunakan teori-urutan serta deskripsi aljabar.
Kisi sebagai himpunan berurutan sebagian
Jika (L, ≤) adalah himpunan berurutan sebagian (pohimpunan), dan S ⊆ L adalah himpunan bagian arbitrer, maka elemen u ∈ L adalah sebagai batas atas dari S jika s ≤ u untuk s ∈ S. Batas atas u dari S sebagai batas bagian atas, atau gabung, supremum, jika u ≤ x untuk batas atas x dari S. Satu himpunan dari batad atas terkecil, tidak lebih dari satu. Dualitas l ∈ L sebagai batas bawah dari S jika l ≤ s untuk s ∈ S. Batad bawah l dari S sebagai batas bawah terbesar, atau bertemu, minimal, jika x ≤ l untuk batad bawah x dari S.
Rangkaian urutan sebagian (L, ≤) disebut gabung-semikisi jika himpunan bagian dua elemen {a, b} ⊆ L memiliki gabungan (yaitu batas atas terkecil), dan disebut bertemu-semikisi jika himpunan bagian dua elemen memiliki pertemuan (yaitu batas bawah terbesar), dilambangkan dengan a ∨ b dan a ∧ b. (L, ≤) disebut kisi jika gabungan dan bertemu-semikisi. Definisi ∨ dan ∧ adalah operasi biner. Kedua operasi tersebut monoton dengan urutan: a1 ≤ a2 dan b1 ≤ b2 dengan a1 ∨ b1 ≤ a2 ∨ b2 dan a1 ∧ b1 ≤ a2 ∧ b2.
Argumen induksi bahwa himpunan bagian hingga tidak kosong dari kisi memiliki batas atas terkecil dan batas bawah terbesar. Dengan asumsi tambahan, kesimpulan lebih lanjut dimungkinkan; lihat Kompleknes (teori order) untuk diskusi lebih lanjut tentang subjek ini. Bagaimana dapat mengubah definisi di atas dalam kaitannya dengan keberadaan koneksi Galois diantara himpunan terurut sebagian terkait, pendekatan khusus untuk teori kategori pendekatan kisi, dan untuk analisis konsep formal.
Batas kisi adalah kisi dengan elemen terbesar (juga disebut elemen maksimum, atau atas, dan dilambangkan dengan 1, atau dengan ) dan elemen terkecil (juga disebut minimum, atau bawah, dilambangkan dengan 0 atau dengan ), yaitu
- 0 ≤ x ≤ 1 untuk x di L.
Kisi dibatasi dengan menambahkan elemen buatan terbesar dan terkecil, dan kisi hingga tidak kosong dibatasi, dengan gabungan (berurutan dengan gabung dan bertemu) dari semua elemen, dilambangkan dengan (berurutan ) dimana .
Himpunan berurutan sebagian adalah kisi hingga jika dan hanya jika himpunan elemen hingga (termasuk himpunan kosong) yaitu gabungan dan pertemuan. Untuk elemen x dari sebuah poset tirivial (adalah prinsip vacuous) dan , dan elemen poset adalah batas atas dan batas bawah dari himpunan kosong. Gabungan dari himpunan kosong adalah elemen terkecil , dan bertemu himpunan kosong adalah elemen terbesar . Asosiatif dan komutatifitas bertemu dan gabungan: gabungan dari gabungan himpunan berhingga sama dengan gabungan himpunan, dan dua kali, pertemuan gabungan himpunan hingga sama dengan pertemuan pertemuan himpunan, yaitu, untuk himpunan bagian hingga A dan B dari poset L,
dan
B adalah himpunan kosong,
dan
konsisten dengan .
Elemen kisi y dengan elemen penutup x, jika y > x, maka z adalah y > z > x.[1]
Kisi sebagai struktur aljabar
Kisi umum
Struktur aljabar , dari himpunan dan dua biner, operasi komutatif dan asosiatif , dan , adalah kisi jika identitas aksiomatik berikut untuk elemen disebut hukum absorpsi.
Dua identitas berikut sebagai aksioma, keduanya menggunakan dua hukum absorpsi.[note 1] Maka ini disebut hukum idempoten.
Aksioma menggunakan dan adalah semikisi. Hukum absorpsi, dari aksioma di atas di mana keduanya bertemu dan bergabung, membedakan kisi dari sembarang struktur semikisi dan memastikan bahwa dua semikisi berinteraksi dengan tepat. Secara khusus, setiap semikisi adalah dualitas dari yang lain.
Kisi hingga
Kisi hingga adalah struktur aljabar dengan bentuk dan adalah kisi (kisi bawah) dari elemen identitas untuk operasi penggabungan , dan (bagian atas kisi) adalah elemen identitas untuk operasi meet .
Lihat semikisi untuk informasi lebih lanjut.
Koneksi ke struktur aljabar lainnya
Kisi memiliki beberapa koneksi ke relasi struktur aljabar grup. Karena bertemu dan bergabung dengan komute dan asosiasi, kisi dapat dianggap terdiri dari dua komutatif semigrup yang memiliki domain yang sama. Untuk kisi hingga, semigrup sebenarnya adalah komutatif monoid. Hukum absorpsi adalah identitas penentu dalam teori kisi.
Dengan komutatifitas, asosiatif, dan idempotensi, gabung dan bertemu sebagai operasi pada himpunan hingga tidak kosong, bukan pada relasi elemen. Dalam kisi hingga, gabungan dan pertemuan dari himpunan kosong juga mendefinisikan (sebagai dan ). Hal ini membuat kisi hingga dari kisi umum, dan banyak penulis mengharuskan semua kisi menggunakan batas.
Interpretasi aljabar kisi antara peran penting dalam aljabar universal.
Relasi antara dua definisi
Kisi teori-orde antara dua operasi biner ∨ dan ∧. Karena hukum komutatif, asosiatif dan absorpsi dengan diverifikasi untuk operasi, maka (L, ∨, ∧) dalam kisi dalam arti aljabar.
Kebalikannya, dengan kisi ditentukan aljabar (L, ∨, ∧), satu menentukan urutan parsial ≤ di L dengan
- a ≤ b jika a = a ∧ b, atau
- a ≤ b jika b = a ∨ b,
untuk elemen a dan b dari L. Hukum absorpsi bahwa kedua definisi adalah ekuivalen:
a = a ∧ b dengan b = b ∨ (b ∧ a) = (a ∧ b) ∨ b = a ∨ b
dan dualitas untuk arah lain.
Relasi ≤ digunakan untuk mendefinisikan urutan parsial di mana biner bertemu dan bergabung diberikan melalui operasi asli ∨ dan ∧.
Karena dua definisi kisi adalah ekuivalen, dengan menggunakan aspek dari kedua definisi tersebut dengan tujuan digunakan.
Contoh
-
Gambar 1: Himpunan bagian dari {x, y, z}, di bawah himpunan inklusi. Nama "kisi" disarankan oleh bentuk diagram Hasse yang menggambarkannya.
-
Gambar 2: Kisi pembagi bilangan bulat 60, diurutkan dengan "membagi".
-
Gambar 3: Kisi partisi dari {1, 2, 3, 4}, order dari "refines".
-
Gambar 4: Kisi bilangan bulat positif, diurutkan dari ≤.
-
Gambar 5: Kisi pasangan bilangan bulat nonnegatif, diurutkan berdasarkan komponen.
- Untuk himpunan A, himpunan bagian dari A (disebut himpunan pangkat dari A) urutan himpunan bagian inklusi untuk kisi hingga A dengan himpunan kosong. Himpunan perpotongan dan satuan menafsirkan bertemu dan bergabung (lihat Gambar 1).
- Untuk himpunan A, himpunan bagian hingga dari A, diurutkan dengan penyertaan, juga merupakan kisi, dan dibatasi jika dan hanya jika A hingga.
- Untuk himpunan A, diurutkan dengan partisi adalah kisi (lihat Gambar 3).
- Bilangan bulat positif dalam urutan membentuk kisi, di bawah operasi "min" dan "max". 1 bagian bawah; tidak memiliki bagian atas (lihat Gambar 4).
- Persegi Kartesius dari bilangan asli, diurutkan sehingga (a, b) ≤ (c, d) jika a ≤ c dan b ≤ d. Relasi (0, 0) adalah elemen bawah; tidak memiliki bagian atas (lihat Gambar 5).
- Bilangan asli dari bentuk kisi di bawah operasi pembagi persekutuan terbesar dan kelipatan persekutuan terkecil, dengan persekutuan sebagai relasi urutan: a ≤ b jika a membagi b maka 1 bagian bawah; 0 teratas. Gambar 2 menunjukkan subkisi hingga.
- Kisi kompleks adalah kisi hingga (spesifik). Kelas dari praktisi contoh.
- Himpunan elemen kompak dari aritmetika kisi kompleks adalah kisi dengan elemen terkecil, dimana operasi kisi dengan membatasi operasi kisi aritmetika. Sifat khusus yang membedakan kisi aritmetika dari kisi aljabar, dimana pemadatannya hanya membentuk gabungan-semikisi. Kedua kelas kisi kompleks dipelajari di teori domain.
Contoh kisi lebih lanjut untuk sifat tambahan yang dibahas di bawah ini.
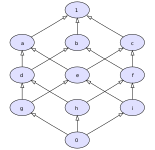
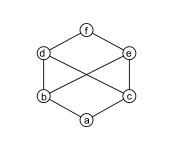
Contoh non-kisi
 |
 |
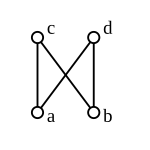 |
Sebagian besar rangkaian yang diurutkan sebagian bukanlah kisi, termasuk berikut ini.
- Poset diskrit, artinya poset x ≤ y dengan x = y, adalah kisi jika dan hanya jika memiliki banyak satu elemen. Secara khusus, poset diskrit dua elemen bukanlah kisi.
- Maka himpunan {1, 2, 3, 6} sebagian diurutkan berdasarkan pembagian adalah kisi, himpunan {1, 2, 3} jadi bukan kisi karena urutan 2, 3 tidak memiliki gabungan; maka, 2, 3 tidak memiliki pertemuan {2, 3, 6}.
- Himpunan {1, 2, 3, 12, 18, 36} sebagian urutan pembagian bukan kisi. Bagian elemen memiliki batas atas dan batas bawah, tetapi 2, 3 memiliki tiga batas atas, yaitu 12, 18, dan 36, tidak memiliki terkecil dari ketiga yang dapat dibagi. Bagian 12, 18 memiliki tiga batas bawah, yaitu 1, 2, dan 3, tidak memiliki bagian terbesar dari ketiganya yang dapat dibagi (2 dan 3 tidak saling membagi).
Morfisme kisi

Gagasan tentang morfisme antara dua kisi mengalir dengan mudah dari definisi aljabar atas. Maka dua kisi (L, ∨L, ∧L) dan (M, ∨M, ∧M), kisi homomorfisme dari L menjadi M adalah fungsi f : L → M untuk a, b ∈ L:
- f(a ∨L b) = f(a) ∨M f(b), dan
- f(a ∧L b) = f(a) ∧M f(b).
Jadi f adalah homomorfisme dari dua semikisi. Jika kisi dengan struktur. Secara khusus, homomorfisme kisi berbatas (biasanya disebut "homomorfisme kisi") f antara dua kisi berbatas L dan M memiliki sifat berikut:
- f(0L) = 0M , and
- f(1L) = 1M .
Dalam rumus teori-ordo, bahwa homomorfisme kisi adalah fungsi pengawetan pertemuan dan penggabungan biner. Untuk kisi berbatas, penggunaan elemen terkecil dan terbesar gabungan dan pertemuan himpunan kosong.
Homomorfisme kisi monoton dengan relasi keteraturan terkait; lihat Fungsi pemeliharaan batas. Kebalikannya tidak benar: monotonisitas tidak menggunakan untuk bertemu dan bergabung (lihat Gambar 9), meskipun pemelihara order bijeksi adalah homomorfisme dari fungsi pembalikan.
Maka dan antara dua kisi dengan 0 dan 1. Homomorfisme dari ke disebut separating-0,1 jika dan hanya jika ( yaitu 0) dan ( yaitu 1).
Lihat pula
- Gabungan dan bertemu
- Peta kisi
- Kisi Orthocomplemented
- Total order
- Ideal dan filter (gagasan ganda)
- Skew lattice (generalisasi untuk non-commutative join and meet)
- Kisi Eulerian
- Kisi Post
- Kisi Tamari
- Kisi-kisi Muda – Fibonacci
- kisi sederhana-0,1
Aplikasi yang menggunakan teori kisi
Perhatikan bahwa dalam banyak aplikasi, set hanya berupa kisi parsial: tidak elemen memiliki pertemuan atau penggabungan.
- Topologi Pointless
- Kisi subgrup
- Ruang spektral
- Subruang varian
- Operator penutupan
- Interpretasi abstrak
- Kisi subsumsi
- Teori himpunan Fuzzy
- Algebraizasi logika orde pertama
- Semantik bahasa pemrograman
- Teori domain
- Ontologi (ilmu komputer)
- Warisan berganda
- Analisis konsep formal dan penambang kisi (teori dan alat)
- Filter Bloom
- Aliran informasi
- Pengoptimalan ordinal
- Logika kuantum
- Grafik median
- Ruang kaji
- Induksi bahasa reguler
- Pemodelan analogis
Catatan
- ^ a ∨ a = a ∨ (a ∧ (a ∨ a)) = a, dan dua kali untuk hukum idempoten lainnya.Dedekind, Richard (1897), "Über Zerlegungen von Zahlen durch ihre grössten gemeinsamen Teiler", Braunschweiger Festschrift: 1–40.
Referensi
- ^ Grätzer 1996, hlm. 52.
Monographs available free online:
- Burris, Stanley N., and Sankappanavar, H. P., 1981. A Course in Universal Algebra. Springer-Verlag. ISBN 3-540-90578-2.
- Jipsen, Peter, and Henry Rose, Varieties of Lattices, Lecture Notes in Mathematics 1533, Springer Verlag, 1992. ISBN 0-387-56314-8.
- Nation, J. B., Notes on Lattice Theory. Chapters 1-6. Chapters 7–12; Appendices 1–3.
Elementary texts recommended for those with limited mathematical maturity:
- Donnellan, Thomas, 1968. Lattice Theory. Pergamon.
- Grätzer, George, 1971. Lattice Theory: First concepts and distributive lattices. W. H. Freeman.
The standard contemporary introductory text, somewhat harder than the above:
- Davey, B. A.; Priestley, H. A. (2002), Introduction to Lattices and Order, Cambridge University Press, ISBN 978-0-521-78451-1
Advanced monographs:
- Garrett Birkhoff, 1967. Lattice Theory, 3rd ed. Vol. 25 of AMS Colloquium Publications. American Mathematical Society.
- Robert P. Dilworth and Crawley, Peter, 1973. Algebraic Theory of Lattices. Prentice-Hall. ISBN 978-0-13-022269-5.
- Grätzer, George (1996) [1978]. General Lattice Theory
 (edisi ke-Second). Basel: Birkhäuser. ISBN 978-3-7643-6996-5.
(edisi ke-Second). Basel: Birkhäuser. ISBN 978-3-7643-6996-5.
On free lattices:
- R. Freese, J. Jezek, and J. B. Nation, 1985. "Free Lattices". Mathematical Surveys and Monographs Vol. 42. Mathematical Association of America.
- Johnstone, P. T., 1982. Stone spaces. Cambridge Studies in Advanced Mathematics 3. Cambridge University Press.
On the history of lattice theory:
- Štĕpánka Bilová (2001). Eduard Fuchs, ed. Lattice theory — its birth and life (PDF). Prometheus. hlm. 250–257.
On applications of lattice theory:
- Garrett Birkhoff (1967). James C. Abbot, ed. What can Lattices do for you?. Van Nostrand. Table of contents
Pranala luar
- Hazewinkel, Michiel, ed. (2001) [1994], "Lattice-ordered group", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
- Weisstein, Eric W. "Lattice". MathWorld.
- J.B. Nation, Notes on Lattice Theory, unpublished course notes available as two PDF files.
- Ralph Freese, "Lattice Theory Homepage".
- Templat:OEIS el



















































