Bilangan bulat: Perbedaan antara revisi

Konten dihapus Konten ditambahkan

Sebaris

Revisi terkini sejak 24 Oktober 2024 23.54

Bilangan bulat dapat dianggap sebagai titik-titik diskret yang berjarak sama sepanjang garis bilangan. Pada gambar ini, bilangan-bilangan bulat positif ditandai dengan warna hijau dan bilangan-bilangan bulat negatif dengan warna biru.

Bilangan bulat adalah bilangan yang dapat dituliskan tanpa komponen desimal atau pecahan. Sebagai contoh, 21, 4, 0, -3, -67 dan -2048 merupakan bilangan bulat, sedangkan 9,75 , 5 12 , dan ${\sqrt {5}}$ bukan.

Himpunan bilangan bulat terdiri dari angka 0, semua bilangan bulat positif $\{1,2,3,\dots \}$ (juga disebut dengan bilangan asli), dan invers aditif-nya, semua bilangan bulat negatif $\{-1,-2,-3,\dots \}$ .^[1]^[2] Dalam matematika, himpunan ini sering dilambangkan dengan $\mathbb {Z}$ ,^[3] atau huruf tebal ( $\mathbf {Z}$ ). Huruf kapital Z yang digunakan berasal dari kata Zahlen, yang berarti bilangan dalam bahasa Jerman.^[4]^[5]^[6]^[7]

Himpunan bilangan bulat merupakan subhimpunan dari himpunan bilangan rasional, sekaligus juga dari bilangan riil.

Subhimpunan $\mathbb {Z}$ yang hanya terdiri dari angka 0 dan bilangan-bilangan bulat positif disebut dengan bilangan cacah.^[8] Himpunan $\mathbb {Z}$ sendiri merupakan subhimpunan dari himpunan bilangan rasional,^[9] karena nilainya dapat ditulis sebagai pecahan dengan penyebut 1. Bilangan rasional selanjutnya merupakan subhimpunan dari himpunan bilangan riil.^[10]

Notasi

Simbol $\mathbb {Z}$ sebagai himpunan bilangan bulat digunakan oleh banyak penulis untuk menyatakan beberapa jenis himpunan.

Notasi $\mathbb {Z} ^{+}$ ,^[11] $\mathbb {Z} _{+}$ , atau $\mathbb {Z} ^{>}$ , digunakan untuk melambangkan bilangan bulat positif (disebut juga bilangan asli).
Notasi $\mathbb {Z} ^{-}$ melambangkan bilangan bulat negatif.^[12]
Notasi bilangan bulat taknegatif dapat ditulis sebagai $\mathbb {Z} ^{0+}$ atau $\mathbb {Z} ^{\geq }$
Notasi bilangan bulat taknol ditulis $\mathbb {Z} ^{\neq 0}$ atau $\mathbb {Z} ^{*}$ .^{[nb 1]}

Notasi lain yang berkaitan dengan simbol himpunan bilangan bulat adalah $\mathbb {Z} _{n}$ , yang melambangkan himpunan bilangan bulat modulo- $n$ , yaitu himpunan semua kelas kekongruenan dari bilangan bulat modulo $n$ . Sedangkan notasi $\mathbb {Z} ^{n}$ melambangkan kekisi bilangan bulat.^[13] Notasi lainnya, yaitu ${\tfrac {1}{2}}\mathbb {Z}$ melambangkan setengah bilangan bulat.^[14]

Sifat-sifat aljabar

Seperti himpunan bilangan asli, $\mathbb {Z}$ tertutup terhadap operasi penjumlahan dan perkalian. Artinya, penjumlahan maupun perkalian dari dua bilangan bulat akan menghasilkan bilangan bulat.^[15]^[16] $\mathbb {Z}$ juga tertutup terhadap operasi pengurangan karena mengandung 0 dan bilangan-bilangan negatif, berbeda halnya dengan bilangan asli. Namun karena hasil pembagian dua bilangan bulat belum tentu berupa bilangan bulat pula (contohnya 1 ketika dibagi dengan 2), $\mathbb {Z}$ tidak tertutup terhadap pembagian. Walaupun bilangan asli tertutup terhadap eksponensiasi, sifat ini tidak berlaku pada bilangan bulat, karena hasil eksponensiasi dapat berbentuk pecahan ketika eksponen bernilai negatif.

Tabel berikut berisi daftar beberapa sifat dasar operasi penambahan dan perkalian, untuk sembarang bilangan bulat $a$ , $b$ , dan $c$ :

	Penambahan	Perkalian
Ketertutupan	$a+b$ adalah bilangan bulat	$a\times b$ adalah bilangan bulat
Asosiatif	$a+(b+c)=(a+b)+c$	$a\times (b\times c)=(a\times b)\times c$
Komutatif	$a+b=b+a$	$a\times b=b\times a$
Elemen identitas	$a+0=a$	$a\times 1=a$
Elemen invers	$a+(-a)=0$	$a\times {\frac {1}{a}}=1$
Distributif	$a\times (b+c)=(a\times b)+(a\times c)$

Empat sifat pertama untuk perkalian yang ditulis dalam tabel, menyatakan bahwa $\mathbb {Z}$ dalam operasi perkalian merupakan suatu monoid komutatif. Namun, tidak semua bilangan bulat memiliki invers perkalian (contohnya angka 2), mengakibatkan $\mathbb {Z}$ dalam perkalian bukan suatu grup. Tidak lengkapnya invers perkalian untuk setiap elemen setara dengan pernyataan $\mathbb {Z}$ tidak tertutup dalam pembagian, mengartikan bahwa $\mathbb {Z}$ bukan suatu lapangan. Lapangan terkecil yang mengandung bilangan bulat sebagai sublapangan adalah lapangan bilangan rasional.

Lima sifat pertama untuk penjumlahan yang ditulis dalam tabel, menyatakan bahwa $\mathbb {Z}$ dalam penjumlahan merupakan suatu grup Abelian. Himpunan $\mathbb {Z}$ juga merupakan suatu grup siklik, karena semua bilangan bulat bukan 0 dapat ditulis sebagai penjumlahan terhingga $1+1+\dots +1$ atau $(-1)+(-1)+\dots +(-1)$ . Malahan, $\mathbb {Z}$ dalam penjumlahan adalah satu-satunya grup siklik tak hingga — dalam artian semua grup siklik tak hingga bersifat isomorfik dengan $\mathbb {Z}$ .

Semua sifat pada tabel (kecuali baris terakhir), ketika digunakan bersama-sama, mengartikan bahwa $\mathbb {Z}$ dengan penjumlahan dan perkalian membentuk suatu gelanggang komutatif dengan elemen identitas. Gelanggang ini adalah fondasi semua objek struktur aljabar.

Walaupun pembagian yang umum tidak terdefinisi di $\mathbb {Z}$ , operasi pembagian "dengan sisa" dapat didefinisikan. Pembagian ini disebut pembagian Euklides, dan memiliki sifat penting berikut: untuk sembarang dua bilangan bulat $a$ dan $b$ dengan $b\neq 0$ , akan ada bilangan bulat unik $q$ dan $r$ yang memenuhi $a=qb+r$ dan $0\leq r<|b|$ , dengan notasi $|b|$ berarti nilai mutlak dari $b$ . Bilangan $q$ disebut hasil bagi dan $r$ disebut sisa pembagian $a$ oleh $b$ . Algoritme Euklides menggunakan serangkaian operasi pembagian Euklides untuk menghitung faktor persekutuan terbesar.

Sifat keterurutan

Himpunan bilangan bulat dapat diurutkan, secara alami dari nilai terkecil hingga terbesar: $\cdots <-3<-2<-1<0<1<2<3<\cdots$ . Dua bilangan bulat dibandingkan dengan lambang-lambang yaitu lebih dari, kurang dari, lebih dari atau sama dengan, atau kurang dari atau sama dengan, masing-masing dilambangkan sebagai $>$ , $<$ , $\geq$ , dan $\leq$ . Bilangan bulat disebut bilangan positif jika nilainya $>0$ dan disebut bilangan negatif jika nilainya $<0$ . Sedangkan penggunaan tanda $\leq$ menyatakan bahwa bilangan tidak positif, dan penggunaan tanda $\geq$ menyatakan bahwa bilangan tidak negatif.^[17]

Pengurutan bilangan bulat kompatibel dengan sifat-sifat aljabar, dalam artian:

Jika $a<b$ dan $c<d$ , maka $a+c<b+d$
Jika $a<b$ dan $0<c$ , maka $ac<bc$

Hal ini menyimpulkan $\mathbb {Z}$ dan definisi keterurutan di atas akan membentuk suatu gelanggang terurut.

Konstruksi

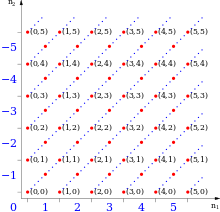
Dalam pengajaran di sekolah, bilangan bulat umumnya didefinisikan secara intuitif sebagai kumpulan bilangan asli, angka nol, dan negatif dari kumpulan bilangan asli (maksudnya $\{-1,-2,-3,\dots \}$ ). Namun, definisi ini memerlukan banyak kasus (setiap operasi perlu didefinisikan untuk setiap kombinasi jenis bilangan) dan menyulitkan untuk membuktikan bahwa bilangan bulat memenuhi berbagai rumus aritmetika.^[18] Karena itu, matematika yang modern menggunakan definisi yang lebih lebih abstrak,^[19] yang memungkinkan operasi-operasi aritmetika didefinisikan tanpa perlu membaginya dalam kasus-kasus.^[20] Bilangan bulat selanjutnya dikonstruksi (didefinisikan) secara formal sebagai kelas-kelas ekuivalensi dari pasangan terurut bilangan asli $(a,b)$ .^[21]

Pasangan $(a,b)$ dapat dianggap sebagai hasil dari mengurangi $b$ dari $a$ .^[21] Untuk memastikan bahwa 1 − 2 dan 4 − 5 menghasilkan bilangan yang sama, relasi ekuivalensi $~$ didefinisikan pada pasangan-pasangan ini dengan aturan:

(a,b)\sim (c,d)

tepat ketika

a+d=b+c

.

Operasi penjumlahan dan perkalian bilangan bulat selanjutnya dapat didefinisikan dalam operasi ekuivalensi pada bilangan asli.^[21] Dengan menggunakan notasi $[(a,b)]$ untuk menyatakan kelas ekuivalensi yang memiliki $(a,b)$ sebagai anggota, dapat dituliskan:

[(a,b)]+[(c,d)]:=[(a+c,b+d)]

.

[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]

.

Invers (lawan) penjumlahan dari suatu bilangan bulat dapat dihasilkan dengan menukar urutan dari pasangan:

-[(a,b)]:=[(b,a)]

.

Sehingga operasi pengurangan dapat didefinisikan sebagai penjumlahan dari invers penjumlahan:

[(a,b)]-[(c,d)]:=[(a+d,b+c)]

.

Pengurutan yang standar pada bilangan-bilangan bulat dapat dituliskan sebagai:

[(a,b)]<[(c,d)]

jika dan hanya jika

a+d<b+c

.

Lebih lanjut, setiap kelas ekuivalen memiliki satu anggota unik yang berbentuk $(n,0)$ atau $(0,n)$ (atau keduanya secara bersamaan). Sehingga pada gilirannya, kelas $[(n,0)]$ dapat diwakilkan oleh bilangan asli $n$ , sedangkan kelas $[(0,n)]$ diwakilkan oleh bilangan $-n$ . Angka $-0=0$ mewakili kelas $[(0,0)]$ . Secara umum, kelas $[(a,b)]$ diwakili oleh bilangan bulat

{\begin{cases}a-b,&{\mbox{jika }}a\geq b\\-(b-a),&{\mbox{jika }}a<b\end{cases}}

Cara konstruksi bilangan bulat seperti di atas menghasilkan representasi bilangan bulat sebagai $\{\dots ,-2,-1,0,1,2,\dots \}$ yang familiar. Berikut beberapa contoh bilangan bulat dan kelas ekuivalen yang diwakilinya:

{\begin{aligned}0&=[(0,0)]&=[(1,1)]&=\cdots &&=[(k,k)]\\1&=[(1,0)]&=[(2,1)]&=\cdots &&=[(k+1,k)]\\-1&=[(0,1)]&=[(1,2)]&=\cdots &&=[(k,k+1)]\\2&=[(2,0)]&=[(3,1)]&=\cdots &&=[(k+2,k)]\\-2&=[(0,2)]&=[(1,3)]&=\cdots &&=[(k,k+2)]\end{aligned}}

Kardinalitas

Kardinalitas dari himpunan bilangan bulat sama dengan $ℵ 0$ (alef-nol). Pernyataan ini dapat ditunjukkan dengan membuat suatu fungsi bijeksi dari $\mathbb {Z}$ ke himpunan bilangan cacah $\mathbb {N} =\{0,1,2,...\}$ . Fungsi tersebut dapat didefinisikan sebagai

f(x)={\begin{cases}-2x,&{\mbox{jika }}x\leq 0\\2x-1,&{\mbox{jika }}x>0\end{cases}}

Fungsi ini akan menghasilkan grafik (himpunan dari pasangan $(x,f(x))$ sebagai berikut:

\{\dots (-4,8),(-3,6),(-2,4),(-1,2),(0,0),(1,1),(2,3),(3,5),\dots \}

.

Fungsi invers dari bijeksi tersebut didefinisikan sebagai

{\begin{cases}g(2x)=-x\\g(2x-1)=x\end{cases}}

yang menghasilkan grafik

\{(0,0),(1,1),(2,-1),(3,2),(4,-2),(5,-3),\dots \}

.

Dalam ilmu komputer

Dalam ilmu komputer, integer (Bahasa Inggris untuk kata "bilangan bulat") umumnya merupakan suatu tipe data primitif di bahasa-bahasa pemrograman. Namun, tipe data integer hanya dapat merepresentasikan subset dari semua bilangan bulat, karena komputer memiliki kapasitas yang terbatas. Sebagai contoh, tipe data integer dalam bahasa pemrograman Pascal hanya mampu menyimpan bilangan bulat yang bernilai diantara $-32768$ sampai $32767$ . Pada representasi two's complement yang umum digunakan, tanda hanya didefinisikan untuk membedakan "bilangan negatif" dan "bilangan tak negatif", bukan "bilangan negatif, positif, dan 0" (walaupun, sebenarnya komputer juga dapat menentukan apakah suatu nilai integer benar-benar bernilai positif). Pada beberapa bahasa pemrograman, aproksimasi bilangan bulat dengan panjang [digit] konstan (fixed-length integer) umumnya diwakili oleh tipe data int atau Integer (seperti pada Algol68, C, Java, Delphi, dll.).

Representasi bilangan bulat dengan panjang digit fleksibel (bahasa Inggris: variable-length integer representation), seperti tipe data bignums, dapat menyimpan sembarang bilangan bulat asalkan dapat disimpan di memori komputer. Implementasi lain dari tipe data integer menggunakan ukuran yang konstan/tetap, sehingga hanya dapat menyimpan nilai bilangan bulat dalam suatu selang tertentu. Ukuran yang dipakai umumnya merupakan banyaknya bits (4, 8, 16, dst.) atau panjang digit desimal yang mudah diingat (misalnya, 9 digit atau 10 digit).

Perumuman

Bilangan bulat Gauss

Dalam teori bilangan, bilangan bulat Gauss adalah bilangan kompleks, dimana bagian riil dan bagian imajiner adalah bilangan bulat, dengan penambahan dan perkalian biasa terhadap bilangan kompleks akan membentuk ranah integral. Bilangan bulat Gauss dapat dilambangkan sebagai $\mathbf {Z} [i]$ ^[22] dan dapat rumuskan ini sebagai $\mathbf {Z} [i]=\{a+bi\mid a,b\in \mathbb {Z} \}$

Rumus di atas memberikan keterangan, di mana $i$ adalah bilangan khayal.

Bilangan bulat Eisenstein

Bilangan bulat Eisenstein, dinamai dari Gotthold Eisenstein, atau dikenal juga sebagai bilangan bulat Eisenstein–Jacobi, adalah bilangan dengan bentuk $a+b\omega$ .^[23] Bilangan bulat Eisenstein dapat dinyatakan sebagai

\mathbf {Z} [\omega ]=\{a+b\omega \mid a,b\in \mathbb {Z} \}

dimana $\omega ={\frac {-1+i{\sqrt {3}}}{2}}$ .^[23]

Aplikasi bilangan bulat

Sebuah termometer yang menunjukkan suhu sekitar $-17^{\circ }{\mbox{C}}$ .

Salah satu penerapan yang paling umum dan yang paling sering ditemui mengenai bilangan bulat adalah pengukuran kuantitatif yang menyatakan panas dan dingin, disebut suhu. Suhu pada termometer dapat menyatakan skalanya bernilai positif maupun negatif.^[24] Misalnya, terdapat sebuah kota dengan suhu sekitar 23 derajat Celsius. Hal tersebut dapat dituliskan " $23^{\circ }{\mbox{C}}$ ". Contoh lainnya adalah sebuah pegunungan bersalju yang suhu terdinginnya mencapai titik ekstrem, yaitu sekitar $-1^{\circ }{\mbox{C}}$ .

Dalam bidang ekonomi, bilangan bulat diterapkan sebagai keuntungan dan kerugian pada suatu keuangan.^[25] Dalam oseanografi, bilangan bulat dipakai untuk para penyelam dan kapten kapal selam laut untuk mengetahui ketinggian dalam laut — dengan kata lain ketinggian negatif.^[26]

Lihat pula

Catatan kaki

^ Dengan kata lain, ini adalah himpunan bilangan bulat tanpa elemen 0, yakni himpunan $\{\dots ,-2,-1,1,2,\dots \}$ .

Rujukan

^ santoso, Kiki Wahyu (2020-07-21). "√ Pengertian Bilangan Bulat dan Contohnya [LENGKAP] ..." Saintif (dalam bahasa Inggris). Diakses tanggal 2020-08-20.
^ Weisstein, Eric W. "Whole Number". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2021-11-12.
^ "Set of Integers Symbol (ℤ)". wumbo.net. Diarsipkan dari versi asli tanggal 2021-11-14. Diakses tanggal 2021-11-14.
^ "Compendium of Mathematical Symbols". Math Vault (dalam bahasa Inggris). 2020-03-01. Diakses tanggal 2020-08-19.
^ Weisstein, Eric W. "Integer". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2020-08-11.
^ Miller, Jeff (2010-08-29). "Earliest Uses of Symbols of Number Theory". Diarsipkan dari versi asli tanggal 2010-01-31. Diakses tanggal 2010-09-20.
^ Peter Jephson Cameron (1998). Introduction to Algebra. Oxford University Press. hlm. 4. ISBN 978-0-19-850195-4. Diarsipkan dari versi asli tanggal 2016-12-08. Diakses tanggal 2016-02-15.
^ Pasinggi, Yonathan Saba (2019). Kesulitan Memahami Konsep Bilangan Cacah di Sekolah Dasar (PDF). Gowa: Agma. hlm. 17.
^ "Intermediate Algebra, Tutorial 3: Sets of Numbers". www.wtamu.edu. Diakses tanggal 2021-11-15.
^ "CK12-Foundation". flexbooks.ck12.org. Diakses tanggal 2021-11-15.
^ Weisstein, Eric W. "Positive Integer". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2021-11-13.
^ Weisstein, Eric W. "Negative Integer". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2021-11-13.
^ Daniele Micciancio, Lattice Algorithms and Applications, Introduction to Lattices
^ Turaev, V. G. (2010). Quantum invariants of knots and 3-manifolds (edisi ke-2nd rev. ed). Berlin: De Gruyter. hlm. 390. ISBN 978-3-11-022184-8. OCLC 650811823. Pemeliharaan CS1: Teks tambahan (link)
^ Buron, Dozon. "Properties of Multiplication of Integers (Definition and Examples)". BYJUS (dalam bahasa Inggris). Diakses tanggal 2021-11-12.
^ "Closure Property of Integers CBSE Class 7 Math Notes". edusaksham.com. Diakses tanggal 2021-11-12.
^ Abdussakir (2014). Matematika dalam Al-Qur'an (PDF). Malang: UIN-Maliki Press. hlm. 83. ISBN 978-602-958-440-0.
^ Mendelson, Elliott (2008). Number Systems and the Foundations of Analysis. Dover Books on Mathematics. Courier Dover Publications. hlm. 86. ISBN 978-0-486-45792-5. Diarsipkan dari versi asli tanggal 2016-12-08. Diakses tanggal 2016-02-15. .
^ Ivorra Castillo: Álgebra
^ Frobisher, Len (1999). Learning to Teach Number: A Handbook for Students and Teachers in the Primary School. The Stanley Thornes Teaching Primary Maths Series. Nelson Thornes. hlm. 126. ISBN 978-0-7487-3515-0. Diarsipkan dari versi asli tanggal 2016-12-08. Diakses tanggal 2016-02-15. .
^ ^a ^b ^c Campbell, Howard E. (1970). The structure of arithmetic. Appleton-Century-Crofts. hlm. 83. ISBN 978-0-390-16895-5.
^ (Fraleigh 1976, hlm. 286)
^ ^a ^b Weisstein, Eric W. "Eisenstein Integer". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2021-11-15.
^ "Applications of Integers - Math Central". mathcentral.uregina.ca. Diakses tanggal 2021-11-15.
^ "Welcome to CK-12 Foundation | CK-12 Foundation". www.ck12.org. Diakses tanggal 2021-11-15.
^ Wahyudin, Sudrajat (2003). Ensiklopedi Matematika dan Peradaban Manusia. Tarity Samudra Berlian. hlm. 43. ISBN 979-8855-06-X.

Pranala luar

Brilliant Math and Science – Integers

[13] Dengan kata lain, ini adalah himpunan bilangan bulat tanpa elemen 0, yakni himpunan $\{\dots ,-2,-1,1,2,\dots \}$ .

[1] santoso, Kiki Wahyu (2020-07-21). "√ Pengertian Bilangan Bulat dan Contohnya [LENGKAP] ..." Saintif (dalam bahasa Inggris). Diakses tanggal 2020-08-20.

[2] Weisstein, Eric W. "Whole Number". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2021-11-12.

[3] "Set of Integers Symbol (ℤ)". wumbo.net. Diarsipkan dari versi asli tanggal 2021-11-14. Diakses tanggal 2021-11-14.

[4] "Compendium of Mathematical Symbols". Math Vault (dalam bahasa Inggris). 2020-03-01. Diakses tanggal 2020-08-19.

[5] Weisstein, Eric W. "Integer". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2020-08-11.

[6] Miller, Jeff (2010-08-29). "Earliest Uses of Symbols of Number Theory". Diarsipkan dari versi asli tanggal 2010-01-31. Diakses tanggal 2010-09-20.

[Cameron1998-7] Peter Jephson Cameron (1998). Introduction to Algebra. Oxford University Press. hlm. 4. ISBN 978-0-19-850195-4. Diarsipkan dari versi asli tanggal 2016-12-08. Diakses tanggal 2016-02-15.

[8] Pasinggi, Yonathan Saba (2019). Kesulitan Memahami Konsep Bilangan Cacah di Sekolah Dasar (PDF). Gowa: Agma. hlm. 17.

[:6-9] "Intermediate Algebra, Tutorial 3: Sets of Numbers". www.wtamu.edu. Diakses tanggal 2021-11-15.

[10] "CK12-Foundation". flexbooks.ck12.org. Diakses tanggal 2021-11-15.

[11] Weisstein, Eric W. "Positive Integer". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2021-11-13.

[12] Weisstein, Eric W. "Negative Integer". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2021-11-13.

[14] Daniele Micciancio, Lattice Algorithms and Applications, Introduction to Lattices

[15] Turaev, V. G. (2010). Quantum invariants of knots and 3-manifolds (edisi ke-2nd rev. ed). Berlin: De Gruyter. hlm. 390. ISBN 978-3-11-022184-8. OCLC 650811823. Pemeliharaan CS1: Teks tambahan (link)

[:3-16] Buron, Dozon. "Properties of Multiplication of Integers (Definition and Examples)". BYJUS (dalam bahasa Inggris). Diakses tanggal 2021-11-12.

[:2-17] "Closure Property of Integers CBSE Class 7 Math Notes". edusaksham.com. Diakses tanggal 2021-11-12.

[18] Abdussakir (2014). Matematika dalam Al-Qur'an (PDF). Malang: UIN-Maliki Press. hlm. 83. ISBN 978-602-958-440-0.

[19] Mendelson, Elliott (2008). Number Systems and the Foundations of Analysis. Dover Books on Mathematics. Courier Dover Publications. hlm. 86. ISBN 978-0-486-45792-5. Diarsipkan dari versi asli tanggal 2016-12-08. Diakses tanggal 2016-02-15. .

[20] Ivorra Castillo: Álgebra

[21] Frobisher, Len (1999). Learning to Teach Number: A Handbook for Students and Teachers in the Primary School. The Stanley Thornes Teaching Primary Maths Series. Nelson Thornes. hlm. 126. ISBN 978-0-7487-3515-0. Diarsipkan dari versi asli tanggal 2016-12-08. Diakses tanggal 2016-02-15. .

[Campbell-1970-p83-22] Campbell, Howard E. (1970). The structure of arithmetic. Appleton-Century-Crofts. hlm. 83. ISBN 978-0-390-16895-5.

[Fraleigh_1976_286-23] (Fraleigh 1976, hlm. 286)

[:5-24] Weisstein, Eric W. "Eisenstein Integer". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2021-11-15.

[25] "Applications of Integers - Math Central". mathcentral.uregina.ca. Diakses tanggal 2021-11-15.

[26] "Welcome to CK-12 Foundation | CK-12 Foundation". www.ck12.org. Diakses tanggal 2021-11-15.

[27] Wahyudin, Sudrajat (2003). Ensiklopedi Matematika dan Peradaban Manusia. Tarity Samudra Berlian. hlm. 43. ISBN 979-8855-06-X.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[nb 1]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

l b s Sistem bilangan
Himpunan terhitung	Bilangan asli ( $\scriptstyle \mathbb {N}$ ) Bilangan bulat ( $\scriptstyle \mathbb {Z}$ ) Bilangan rasional ( $\scriptstyle \mathbb {Q}$ ) Bilangan aljabar ( $\scriptstyle {\overline {\mathbb {Q} }}$ ) Perioda Bilangan terkomputasi Bilangan aritmetis
Bilangan riil dan cabangan	Bilangan riil ( $\scriptstyle \mathbb {R}$ ) Bilangan kompleks ( $\scriptstyle \mathbb {C}$ ) Kuaternion ( $\scriptstyle \mathbb {H}$ ) Oktonion ( $\scriptstyle \mathbb {O}$ ) Sedenion ( $\scriptstyle \mathbb {S}$ ) Aljabar Cayley–Dickson Bilangan rangkap Bilangan kompleks hiperbolik Bilangan hiperkompleks Bilangan superreal Bilangan irasional Bilangan transenden Bilangan hiperreal Bilangan surreal
Sistem lain	Bilangan kardinal Bilangan ordinal Bilangan p-adik Bilangan supernatural