Aljabar elementer

{\overset {}{\underset {}{x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}}}

Rumus kuadrat, yang merupakan solusi dari persamaan kuadrat

ax^{2}+bx+c=0

dimana

a\neq 0

. Di sini simbol

a, b, c

mewakili bilangan arbitrer, dan

x

adalah variabel yang mewakili solusi persamaan.

Plot dua dimensi (kurva merah) dari persamaan aljabar $y=x^{2}-x-2$

Aljabar elementer adalah bentuk fundamental dan dasar dari aljabar, yang diajarkan kepada murid yang dianggap sedikit atau tidak memiliki pengetahuan tentang matematika yang lebih jauh daripada aritmetika (berhitung). Bila dalam aritmetika hanya bilangan dan operasi aritmetika (seperti +, -, ×, ÷) yang ditemukan, dalam aljabar kita juga menggunakan simbol (seperti x dan y, atau a dan b) untuk mewakili bilangan. Simbol seperti ini disebut sebagai variabel atau peubah. Penggunaan simbol seperti ini berguna karena:

Memungkinkan perampatan (generalisasi) persamaan dan pertidaksamaan aritmetika untuk dinyatakan sebagai hukum (seperti a + b = b + a untuk semua a dan b), dan karena itu merupakan langkah pertama untuk studi sistematis terhadap sifat-sifat sistem bilangan riil.
Memungkinkan merujuk kepada bilangan yang tidak diketahui. Dalam konteks suatu masalah, variabel mungkin mewakili suatu nilai yang belum diketahui, tetapi dapat ditemukan lewat perumusan dan manipulasi persamaan matematika
Memungkinkan penjelajahan hubungan matematika antara besaran-besaran (misalnya, "bila kamu menjual x karcis, keuntunganmu adalah 3x − 1000 rupiah").

Ketiganya adalah untaian utama dari aljabar elementer, yang mesti dibedakan dari aljabar abstrak, yang merupakan wilayah studi lebih lanjut.

Dalam aljabar elementer, sebuah "pernyataan matematika" boleh terdiri dari bilangan, variabel, dan operasi aritmetika. Ini biasanya ditulis dengan 'pangkat yang lebih tinggi' diletakkan di kiri; contohnya:

x+3\,

y^{2}+2x-3\,

z^{7}+a(b+x^{3})+42/y-\pi .\,

Dalam aljabar yang lebih lanjut, suatu pernyataan juga mungkin memiliki fungsi elementer.

Sebuah "persamaan" adalah klaim bahwa dua pernyataan adalah sama. Sebagian persamaan berlaku untuk semua nilai variabel (seperti a + b = b + a). Persamaan seperti ini dinamakan "identitas". Persamaan "bersyarat" berlaku hanya untuk sebagian nilai variabel yang mungkin: x² − 1 = 4. Nilai-nilai variabel yang membuat persamaan tersebut berlaku disebut pemecahan atau "solusi" persamaan.

Notasi aljabar

Notasi aljabar menjelaskan aturan dan ketentuan penulisan ekspresi matematika, serta terminologi yang digunakan untuk membicarakan bagian-bagian ekspresi. Misalnya ekspresi $3x^{2}-2xy+c$ memiliki komponen berikut:

Koefisien adalah nilai numerik, atau huruf yang mewakili konstanta numerik, yang mengalikan variabel (operator dihilangkan). A term adalah adend atau penjumlahan, grup koefisien, variabel, konstanta, dan eksponen yang dapat dipisahkan dari suku lain dengan plus dan minus.^[1] Huruf mewakili variabel dan konstanta. Sesuai ketentuan, huruf di awal alfabet (yaitu $a,b,c$ ) biasanya digunakan untuk mewakili konstanta, dan yang mendekati akhir alfabet (misalnya $x,y$ dan $z$ ) digunakan untuk mewakili variabel .^[2] Biasanya ditulis miring.^[3]

Operasi aljabar bekerja dengan cara yang sama seperti operasi aritmetika,^[4] seperti penambahan, pengurangan, perkalian, pembagian dan eksponensiasi.^[5] dan diterapkan pada variabel dan suku aljabar. Simbol perkalian biasanya dihilangkan, dan diterapkan ketika tidak ada ruang antara dua variabel atau suku, atau ketika koefisien digunakan. Misalnya, $3\times x^{2}$ ditulis sebagai $3x^{2}$ , dan $2\times x\times y$ ditulis $2xy$ .^[6]

Biasanya suku dengan pangkat tertinggi (eksponen), ditulis di sebelah kiri, misalnya, $x^{2}$ ditulis di sebelah kiri $x$ . Ketika koefisien adalah satu, biasanya dihilangkan (misalnya $1x^{2}$ is written $x^{2}$ ).^[7] Begitu juga saat eksponen (pangkat) adalah satu, (misalnya $3x^{1}$ ditulis $3x$ ).^[8] Jika eksponennya nol, hasilnya selalu 1 (misalnya $x^{0}$ selalu ditulis ulang menjadi $1$ ).^[9] Namun $0^{0}$ , karena tidak terdefinisi, seharusnya tidak muncul dalam ekspresi, dan perhatian harus diberikan dalam menyederhanakan ekspresi di mana variabel mungkin muncul dalam eksponen.

Notasi alternatif

Jenis notasi lain digunakan dalam ekspresi aljabar ketika pemformatan yang diperlukan tidak tersedia, atau tidak dapat tersirat, seperti di mana hanya huruf dan simbol variabel. Sebagai ilustrasi, eksponen biasanya diformat menggunakan superskrip, misalnya $x^{2}$ , dalam teks biasa, dan dalam bahasa markup TeX, simbol tanda sisipan "^" mewakili eksponensiasi, jadi $x^{2}$ ditulis sebagai "x^2".,^[10]^[11] serta beberapa bahasa pemrograman seperti Lua. Dalam bahasa pemrograman seperti Ada,^[12] Fortran,^[13] Perl,^[14] Python ^[15] and Ruby,^[16] tanda bintang ganda digunakan, jadi $x^{2}$ ditulis sebagai "x**2". Banyak bahasa pemrograman dan kalkulator menggunakan tanda bintang tunggal untuk mewakili simbol perkalian,^[17] dan itu harus digunakan secara eksplisit, misalnya, $3x$ ditulis "3*x".

Konsep

Variabel

Aljabar elementer dalam aritmetika^[18] dengan memasukkan huruf yang disebut variabel untuk mewakili angka umum (tidak ditentukan). Ini berguna karena beberapa alasan.

Variabel mungkin mewakili angka yang nilainya belum diketahui. Misalnya, jika suhu hari ini, 20 derajat lebih tinggi dari suhu hari sebelumnya, maka P dari soal tersebut dapat dijelaskan secara aljabar sebagai $C=P+20$ .^[19]
Variabel memungkinkan seseorang untuk menggambarkan masalah umum,^[20] tanpa menentukan nilai kuantitas yang terlibat. Misalnya, dapat dinyatakan secara spesifik bahwa 5 menit sama dengan $60\times 5=300$ detik. Deskripsi yang lebih umum (aljabar) mungkin menyatakan bahwa jumlah detik, $s=60\times m$ , dimana m adalah jumlah menit.
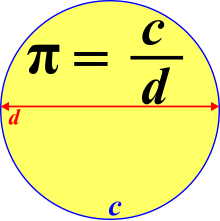
Variabel memungkinkan untuk mendeskripsikan hubungan matematis antara besaran yang mungkin berbeda.^[21] Misalnya, hubungan antara keliling, c, dan diameter, d, dari sebuah lingkaran dijelaskan oleh $\pi =c/d$ .
Variabel memungkinkan untuk mendeskripsikan beberapa properti matematika. Misalnya, sifat dasar penjumlahan adalah komutativitas yang menyatakan bahwa urutan bilangan yang dijumlahkan tidak menjadi masalah. Komutatifitas dinyatakan secara aljabar sebagai $(a+b)=(b+a)$ .^[22]

Menyederhanakan ekspresi

Ekspresi aljabar dapat dievaluasi dan disederhanakan, berdasarkan sifat dasar operasi aritmetika (penambahan, pengurangan, perkalian, pembagian dan eksponensiasi). Sebagai contoh,

Suku ditambahkan dan disederhanakan menggunakan koefisien. Misalnya, $x+x+x$ dapat disederhanakan menjadi $3x$ (dengan 3 adalah koefisien numerik).
Suku yang dikalikan disederhanakan menggunakan eksponen. Sebagai contoh, $x\times x\times x$ direpresentasikan sebagai $x^{3}$
Seperti istilah ditambahkan,^[23] sebagai contoh, $2x^{2}+3ab-x^{2}+ab$ ditulis sebagai $x^{2}+4ab$ , karena istilah yang mengandung $x^{2}$ , dan istilah yang mengandung $ab$ .
Tanda kurung dapat "dikalikan", menggunakan sifat distributif. Misalnya, $x(2x+3)$ dapat ditulis sebagai $(x\times 2x)+(x\times 3)$ ditulis sebagai $2x^{2}+3x$
Ekspresi dapat difaktorkan. Misalnya, $6x^{5}+3x^{2}$ , dengan membagi kedua suku dengan $3x^{2}$ dapat ditulis sebagai $3x^{2}(2x^{3}+1)$

Persamaan

Sebuah persamaan menyatakan bahwa dua ekspresi sama dengan menggunakan simbol persamaan, = (tanda sama dengan).^[24] Salah satu persamaan paling terkenal menjelaskan hukum Pythagoras yang berkaitan dengan panjang sisi segitiga sudut siku-siku:^[25]

c^{2}=a^{2}+b^{2}

Persamaan ini digunakan bahwa $c^{2}$ , merepresentasikan kuadrat dari panjang sisi yang merupakan sisi miring, sisi yang berlawanan dengan sudut siku-siku, sama dengan jumlah (penambahan) kuadrat dari dua sisi lainnya yang panjangnya diwakili oleh $a$ dan $b$ .

Persamaan adalah dua ekspresi memiliki nilai yang sama dan sama. Beberapa persamaan benar untuk semua nilai variabel yang terlibat (seperti $a+b=b+a$ ); persamaan disebut identitas. Persamaan kondisional benar hanya untuk beberapa nilai dari variabel yang terlibat, misalnya $x^{2}-1=8$ hanya benar untuk $x=3$ and $x=-3$ . Nilai variabel yang membuat persamaan menjadi benar adalah solusi dari persamaan dan dapat ditemukan melalui pemecah persamaan.

Jenis persamaan lainnya adalah pertidaksamaan. Pertidaksamaan digunakan untuk menunjukkan bahwa satu sisi persamaan lebih besar, atau lebih kecil, dari sisi lainnya. Simbol yang digunakan untuk ini adalah: $a>b$ di mana $>$ mewakili 'lebih besar dari', dan $a<b$ dimana $<$ mewakili 'kurang dari'. Sama seperti persamaan persamaan standar, angka dapat ditambahkan, dikurangi, dikalikan atau dibagi. Satu-satunya pengecualian adalah saat mengalikan atau membagi dengan bilangan negatif, simbol pertidaksamaan harus dibalik.

Substitusi

Substitusi menggantikan suku-suku dalam suatu ekspresi untuk membuat ekspresi baru. Mengganti 3 untuk $a$ dalam ekspresi tersebut $a *5$ membuat ekspresi baru $3*5$ dengan arti $15$ . Mengganti istilah pernyataan membuat pernyataan baru. Jika pernyataan asli benar secara independen dari nilai istilah, pernyataan yang dibuat oleh substitusi juga benar. Oleh karena itu, definisi dapat dibuat dalam istilah simbolik dan ditafsirkan melalui substitusi: jika $a^{2}:=a\times a$ dimaksudkan sebagai definisi dari $a^{2},$ karena produk dari $a$ dengan dirinya sendiri, menggantikan $3$ untuk $a$ menginformasikan kepada pembaca pernyataan ini bahwa $3^{2}$ sebagai $3 \times 3 = 9$ . Seringkali tidak diketahui apakah pernyataan itu benar terlepas dari nilai istilah. Dan, substitusi memungkinkan untuk mendapatkan batasan pada nilai yang mungkin, atau menunjukkan kondisi apa yang dipegang pernyataan itu. Misalnya, pernyataan $x + 1 = 0$ , if $x$ diganti dengan $1$ , ini menyiratkan $1 + 1 = 2 = 0$ , yang salah, yang menyiratkan bahwa jika $x + 1 = 0$ maka $x$ tidak bisa menjadi $1$ .

Lihat pula

Referensi

Leonhard Euler, Elements of Algebra, 1770. English translation Tarquin Press, 2007, ISBN 978-1-899618-79-8, also online digitized editions^[26] 2006,^[27] 1822.
Charles Smith, A Treatise on Algebra, in Cornell University Library Historical Math Monographs.
Redden, John. Elementary Algebra Diarsipkan 2016-06-10 di Wayback Machine.. Flat World Knowledge, 2011

^ Richard N. Aufmann, Joanne Lockwood, Introductory Algebra: An Applied Approach, Publisher Cengage Learning, 2010, ISBN 1439046042, 9781439046043, page 78
^ William L. Hosch (editor), The Britannica Guide to Algebra and Trigonometry, Britannica Educational Publishing, The Rosen Publishing Group, 2010, ISBN 1615302190, 9781615302192, page 71
^ James E. Gentle, Numerical Linear Algebra for Applications in Statistics, Publisher: Springer, 1998, ISBN 0387985425, 9780387985428, 221 halaman, [James E. Gentle halaman 183]
^ Horatio Nelson Robinson, New elementary algebra: containing the rudiments of science for schools and academies, Ivison, Phinney, Blakeman, & Co., 1866, page 7
^ Ron Larson, Robert Hostetler, Bruce H. Edwards, Algebra And Trigonometry: A Graphing Approach, Publisher: Cengage Learning, 2007, ISBN 061885195X, 9780618851959, 1114 pages, page 6
^ Sin Kwai Meng, Chip Wai Lung, Ng Song Beng, "Algebraic notation", in Mathematics Matters Secondary 1 Express Textbook, Publisher Panpac Education Pte Ltd, ISBN 9812738827, 9789812738820, page 68
^ David Alan Herzog, Teach Yourself Visually Algebra, Publisher John Wiley & Sons, 2008, ISBN 0470185597, 9780470185599, 304 halaman, page 72
^ John C. Peterson, Technical Mathematics With Calculus, Publisher Cengage Learning, 2003, ISBN 0766861899, 9780766861893, 1613 halaman, page 31
^ Jerome E. Kaufmann, Karen L. Schwitters, Algebra for College Students, Publisher Cengage Learning, 2010, ISBN 0538733543, 9780538733540, 803 pages, halaman 222
^ Ramesh Bangia, Dictionary of Information Technology, Publisher Laxmi Publications, Ltd., 2010, ISBN 9380298153, 9789380298153, page 212
^ George Grätzer, Langkah Pertama di LaTeX, Publisher Springer, 1999, ISBN 0817641327, 9780817641320, halaman 17
^ S. Tucker Taft, Robert A. Duff, Randall L. Brukardt, Erhard Ploedereder, Pascal Leroy, Ada 2005 Reference Manual, Volume 4348 dari Catatan Kuliah di Ilmu Komputer, Penerbit Springer, 2007, ISBN 3540693351, 9783540693352, halaman 13
^ C. Xavier, Fortran 77 And Numerical Methods, Penerbit New Age International, 1994, ISBN 812240670X, 9788122406702, halaman 20
^ Randal Schwartz, Brian Foy, Tom Phoenix, Learning Perl, Publisher O'Reilly Media, Inc., 2011, ISBN 1449313140, 9781449313142, halaman 24
^ Matthew A. Telles, Python Power!: The Comprehensive Guide, Publisher Course Technology PTR, 2008, ISBN 1598631586, 9781598631586, halaman 46
^ Kevin C. Baird, Ruby by Example: Concepts and Code, Publisher No Starch Press, 2007, ISBN 1593271484, 9781593271480, page 72
^ William P. Berlinghoff, Fernando Q. Gouvêa, Math through the Ages: A Gentle History for Teachers and Others, Publisher MAA, 2004, ISBN 0883857367, 9780883857366, halaman 75
^ Thomas Sonnabend, Mathematics for Teachers: An Interactive Approach for Grades K-8, Penerbit: Cengage Learning, 2009, ISBN 0495561665, 9780495561668, 759 pages, halaman xvii
^ Lewis Hirsch, Arthur Goodman, Understanding Elementary Algebra With Geometry: A Course for College Students, Penerbit: Cengage Learning, 2005, ISBN 0534999727, 9780534999728, 654 halaman, halaman 48
^ Lawrence S. Leff, College Algebra: Barron's Ez-101 Study Keys, Penerbit: Seri Pendidikan Barron, 2005, ISBN 0764129147, 9780764129148, 230 pages, halaman 2
^ Ron Larson, Kimberly Nolting, Elementary Algebra, Publisher: Cengage Learning, 2009, ISBN 0547102275, 9780547102276, 622 halaman, halaman 210
^ Charles P. McKeague, Elementary Algebra, Penerbit: Cengage Learning, 2011, ISBN 0840064217, 9780840064219, 571 halaman, halaman 49
^ Andrew Marx, Shortcut Algebra I: A Quick and Easy Way to Increase Your Algebra I Knowledge and Test Scores, Penerbit Kaplan Publishing, 2007, ISBN 1419552880, 9781419552885, 288 halaman, halaman 51^{[pranala nonaktif permanen]}
^ Mark Clark, Cynthia Anfinson, Beginning Algebra: Connecting Concepts Through Applications, Pembelajaran Cengage Penerbit, 2011, ISBN 0534419380, 9780534419387, 793 pages, halaman 134
^ Alan S. Tussy, R. David Gustafson, Elementary and Intermediate Algebra, Pembelajaran Cengage Penerbit, 2012, ISBN 1111567689, 9781111567682, 1163 pages, halaman 493
^ Euler's Elements of Algebra Diarsipkan 2011-04-13 di Wayback Machine.
^ Euler, Leonhard; Hewlett, John; Horner, Francis; Bernoulli, Jean; Lagrange, Joseph Louis (4 May 2018). "Elements of Algebra". Longman, Orme. Diakses tanggal 4 May 2018 – via Google Books.

Pranala luar

Media tentang Elementary algebra di Wikimedia Commons

[1] Richard N. Aufmann, Joanne Lockwood, Introductory Algebra: An Applied Approach, Publisher Cengage Learning, 2010, ISBN 1439046042, 9781439046043, page 78

[2] William L. Hosch (editor), The Britannica Guide to Algebra and Trigonometry, Britannica Educational Publishing, The Rosen Publishing Group, 2010, ISBN 1615302190, 9781615302192, page 71

[3] James E. Gentle, Numerical Linear Algebra for Applications in Statistics, Publisher: Springer, 1998, ISBN 0387985425, 9780387985428, 221 halaman, [James E. Gentle halaman 183]

[4] Horatio Nelson Robinson, New elementary algebra: containing the rudiments of science for schools and academies, Ivison, Phinney, Blakeman, & Co., 1866, page 7

[5] Ron Larson, Robert Hostetler, Bruce H. Edwards, Algebra And Trigonometry: A Graphing Approach, Publisher: Cengage Learning, 2007, ISBN 061885195X, 9780618851959, 1114 pages, page 6

[6] Sin Kwai Meng, Chip Wai Lung, Ng Song Beng, "Algebraic notation", in Mathematics Matters Secondary 1 Express Textbook, Publisher Panpac Education Pte Ltd, ISBN 9812738827, 9789812738820, page 68

[7] David Alan Herzog, Teach Yourself Visually Algebra, Publisher John Wiley & Sons, 2008, ISBN 0470185597, 9780470185599, 304 halaman, page 72

[8] John C. Peterson, Technical Mathematics With Calculus, Publisher Cengage Learning, 2003, ISBN 0766861899, 9780766861893, 1613 halaman, page 31

[9] Jerome E. Kaufmann, Karen L. Schwitters, Algebra for College Students, Publisher Cengage Learning, 2010, ISBN 0538733543, 9780538733540, 803 pages, halaman 222

[10] Ramesh Bangia, Dictionary of Information Technology, Publisher Laxmi Publications, Ltd., 2010, ISBN 9380298153, 9789380298153, page 212

[11] George Grätzer, Langkah Pertama di LaTeX, Publisher Springer, 1999, ISBN 0817641327, 9780817641320, halaman 17

[12] S. Tucker Taft, Robert A. Duff, Randall L. Brukardt, Erhard Ploedereder, Pascal Leroy, Ada 2005 Reference Manual, Volume 4348 dari Catatan Kuliah di Ilmu Komputer, Penerbit Springer, 2007, ISBN 3540693351, 9783540693352, halaman 13

[13] C. Xavier, Fortran 77 And Numerical Methods, Penerbit New Age International, 1994, ISBN 812240670X, 9788122406702, halaman 20

[14] Randal Schwartz, Brian Foy, Tom Phoenix, Learning Perl, Publisher O'Reilly Media, Inc., 2011, ISBN 1449313140, 9781449313142, halaman 24

[15] Matthew A. Telles, Python Power!: The Comprehensive Guide, Publisher Course Technology PTR, 2008, ISBN 1598631586, 9781598631586, halaman 46

[16] Kevin C. Baird, Ruby by Example: Concepts and Code, Publisher No Starch Press, 2007, ISBN 1593271484, 9781593271480, page 72

[17] William P. Berlinghoff, Fernando Q. Gouvêa, Math through the Ages: A Gentle History for Teachers and Others, Publisher MAA, 2004, ISBN 0883857367, 9780883857366, halaman 75

[18] Thomas Sonnabend, Mathematics for Teachers: An Interactive Approach for Grades K-8, Penerbit: Cengage Learning, 2009, ISBN 0495561665, 9780495561668, 759 pages, halaman xvii

[19] Lewis Hirsch, Arthur Goodman, Understanding Elementary Algebra With Geometry: A Course for College Students, Penerbit: Cengage Learning, 2005, ISBN 0534999727, 9780534999728, 654 halaman, halaman 48

[20] Lawrence S. Leff, College Algebra: Barron's Ez-101 Study Keys, Penerbit: Seri Pendidikan Barron, 2005, ISBN 0764129147, 9780764129148, 230 pages, halaman 2

[21] Ron Larson, Kimberly Nolting, Elementary Algebra, Publisher: Cengage Learning, 2009, ISBN 0547102275, 9780547102276, 622 halaman, halaman 210

[22] Charles P. McKeague, Elementary Algebra, Penerbit: Cengage Learning, 2011, ISBN 0840064217, 9780840064219, 571 halaman, halaman 49

[23] Andrew Marx, Shortcut Algebra I: A Quick and Easy Way to Increase Your Algebra I Knowledge and Test Scores, Penerbit Kaplan Publishing, 2007, ISBN 1419552880, 9781419552885, 288 halaman, halaman 51^{[pranala nonaktif permanen]}

[24] Mark Clark, Cynthia Anfinson, Beginning Algebra: Connecting Concepts Through Applications, Pembelajaran Cengage Penerbit, 2011, ISBN 0534419380, 9780534419387, 793 pages, halaman 134

[25] Alan S. Tussy, R. David Gustafson, Elementary and Intermediate Algebra, Pembelajaran Cengage Penerbit, 2012, ISBN 1111567689, 9781111567682, 1163 pages, halaman 493

[26] Euler's Elements of Algebra Diarsipkan 2011-04-13 di Wayback Machine.

[27] Euler, Leonhard; Hewlett, John; Horner, Francis; Bernoulli, Jean; Lagrange, Joseph Louis (4 May 2018). "Elements of Algebra". Longman, Orme. Diakses tanggal 4 May 2018 – via Google Books.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

l b s Aljabar
Bidang	Aljabar abstrak Teori kategori Aljabar elementer Teori-K Aljabar komutatif Aljabar nonkomutatif Teori order Aljabar universal
Struktur aljabar	Grup (teori) Gelanggang (teori) Modul (teori) Medan Gelanggang polinomial (Polinomial) Aljabar komposisi
Aljabar linear	Matriks (teori) Ruang vektor (Vektor) Modul Ruang produk dalam (produk titik) Ruang Hilbert
Aljabar multilinear	Aljabar tensor Aljabar eksterior Aljabar simetris Aljabar geometris (Multivektor)
Daftar topik	Aljabar abstrak Struktur aljabar Teori grup Aljabar linear
Glosarium	Aljabar linear Teori medan Teori gelanggang Teori tatanan
Halaman yang terkait	Matematika Sejarah aljabar
Kategori Portal Matematika Wikibuku Dasar Linear Abstrak Wikiversitas Linear Abstrak

l b s Matematika (Bidang matematika)
Fondasi	Filsafat matematika Logika matematika Teori himpunan Teori informasi Teori kategori Teori tipe
Aljabar	Abstrak Elementer Homologis Komutatif Linear Multilinear Universal Teori grup Teori representasi
Analisis	Kalkulus Analisis fungsional Analisis harmonik Analisis kompleks Analisis real Persamaan diferensial Teori ukuran Teori sistem dinamis
Diskret	Kombinatorika Teori graf Teori order
Geometri	Aljabar Analitis Diferensial Diskrit Euklides Hingga Trigonometri
Komputasi	Analisis numerik (Topik) Ilmu komputer Komputasi simbolik Teori komputasi Teori kompleksitas komputasi Optimisasi matematika
Teori bilangan	Aritmetika Geometri Diophantine Teori bilangan aljabar Teori bilangan analitis
Topologi	Teori homotopi Aljabar Diferensial Geometris Umum
Terapan	Matematika biologi Matematika ekonomi Matematika keuangan Fisika matematis Kimia matematika Psikologi matematis Statistika Statistika matematika Teori peluang Ilmu sistem (Teori kendali, Teori permainan, Riset operasi)
Divisi	Matematika murni Matematika terapan Matematika diskret Matematika komputasi
Topik terkait	Matematika dan seni Matematika rekreasi Pendidikan matematika Sejarah matematika
Kategori Portal matematika Kerangka Daftar