Kalkulus: Perbedaan antara revisi

Konten dihapus Konten ditambahkan

Sebaris

Revisi terkini sejak 29 Juni 2023 10.00

Kalkulus (bahasa Latin: calculus, artinya "batu kecil", untuk menghitung) adalah cabang ilmu matematika yang mencakup limit, turunan, integral, dan deret takterhingga. Kalkulus adalah ilmu yang mempelajari perubahan, sebagaimana geometri yang mempelajari bentuk dan aljabar yang mempelajari operasi dan penerapannya untuk memecahkan persamaan. Kalkulus memiliki aplikasi yang luas dalam bidang-bidang sains, ekonomi, dan teknik; serta dapat memecahkan berbagai masalah yang tidak dapat dipecahkan dengan aljabar elementer.^[1]

Kalkulus memiliki dua cabang utama, kalkulus diferensial dan kalkulus integral yang saling berhubungan melalui teorema dasar kalkulus. Contoh cabang kalkulus yang lain adalah kalkulus proposisional, kalkulus variasi, kalkulus lambda, dan kalkulus proses. Pelajaran kalkulus adalah pintu gerbang menuju pelajaran matematika lainnya yang lebih tinggi, yang khusus mempelajari fungsi dan limit, yang secara umum dinamakan analisis matematika.^[1]

Sejarah

*Sir Isaac Newton* adalah salah seorang penemu dan kontributor kalkulus yang terkenal.

Perkembangan

Sejarah perkembangan kalkulus bisa ditilik pada beberapa periode zaman, yaitu zaman kuno, zaman pertengahan, dan zaman modern. Pada periode zaman kuno, beberapa pemikiran tentang kalkulus integral telah muncul, tetapi tidak dikembangkan dengan baik dan sistematis.^[2] Perhitungan volume dan luas yang merupakan fungsi utama dari kalkulus integral bisa ditelusuri kembali pada Papirus Moskwa Mesir (c. 1800 SM). Pada papirus tersebut, orang Mesir telah mampu menghitung volume piramida terpancung.^[3] Archimedes mengembangkan pemikiran ini lebih jauh dan menciptakan heuristik yang menyerupai kalkulus integral.^[4]

Pada zaman pertengahan, matematikawan India, Aryabhata, menggunakan konsep kecil tak terhingga pada tahun 499 dan mengekspresikan masalah astronomi dalam bentuk persamaan diferensial dasar.^[5] Persamaan ini kemudian mengantar Bhāskara II pada abad ke-12 untuk mengembangkan bentuk awal turunan yang mewakili perubahan yang sangat kecil takterhingga dan menjelaskan bentuk awal dari "Teorema Rolle".^[6] Sekitar tahun 1000, matematikawan Irak Ibn al-Haytham (Alhazen) menjadi orang pertama yang menurunkan rumus perhitungan hasil jumlah pangkat empat, dan dengan menggunakan induksi matematika, dia mengembangkan suatu metode untuk menurunkan rumus umum dari hasil pangkat integral yang sangat penting terhadap perkembangan kalkulus integral.^[7] Pada abad ke-12, seorang Persia Sharaf al-Din al-Tusi menemukan turunan dari fungsi kubik, sebuah hasil yang penting dalam kalkulus diferensial.^[8] Pada abad ke-14, Madhava, bersama dengan matematikawan-astronom dari mazhab astronomi dan matematika Kerala, menjelaskan kasus khusus dari deret Taylor,^[9] yang dituliskan dalam teks Yuktibhasa.^[10]^[11]^[12]

Pada zaman modern, penemuan independen terjadi pada awal abad ke-17 di Jepang oleh matematikawan seperti Seki Kowa. Di Eropa, beberapa matematikawan seperti John Wallis dan Isaac Barrow memberikan terobosan dalam kalkulus.^[13] James Gregory membuktikan sebuah kasus khusus dari teorema dasar kalkulus pada tahun 1668.^[14]

Leibniz dan Newton mendorong pemikiran-pemikiran ini bersama sebagai sebuah kesatuan dan kedua orang ilmuwan tersebut dianggap sebagai penemu kalkulus secara terpisah dalam waktu yang hampir bersamaan. Newton mengaplikasikan kalkulus secara umum ke bidang fisika sementara Leibniz mengembangkan notasi-notasi kalkulus yang banyak digunakan sekarang.^[14]

Ketika Newton dan Leibniz mempublikasikan hasil mereka untuk pertama kali, timbul kontroversi di antara matematikawan tentang mana yang lebih pantas untuk menerima penghargaan terhadap kerja mereka. Newton menurunkan hasil kerjanya terlebih dahulu, tetapi Leibniz yang pertama kali mempublikasikannya. Newton menuduh Leibniz mencuri pemikirannya dari catatan-catatan yang tidak dipublikasikan, yang sering dipinjamkan Newton kepada beberapa anggota dari Royal Society.^[15]

Pemeriksaan secara terperinci menunjukkan bahwa keduanya bekerja secara terpisah, dengan Leibniz memulai dari integral dan Newton dari turunan. Sekarang, baik Newton dan Leibniz diberikan penghargaan dalam mengembangkan kalkulus secara terpisah. Adalah Leibniz yang memberikan nama kepada ilmu cabang matematika ini sebagai kalkulus, sedangkan Newton menamakannya "The science of fluxions".^[15]

Sejak itu, banyak matematikawan yang memberikan kontribusi terhadap pengembangan lebih lanjut dari kalkulus. Salah satu karya perdana yang paling lengkap mengenai analisis finit dan infinitesimal ditulis pada tahun 1748 oleh Maria Gaetana Agnesi.^[16]

Pengaruh penting

Walau beberapa konsep kalkulus telah dikembangkan terlebih dahulu di Mesir, Yunani, Tiongkok, India, Iraq, Persia, dan Jepang, penggunaaan kalkulus modern dimulai di Eropa pada abad ke-17 sewaktu Isaac Newton dan Gottfried Wilhelm Leibniz mengembangkan prinsip dasar kalkulus. Hasil kerja mereka kemudian memberikan pengaruh yang kuat terhadap perkembangan fisika.^[14]

Aplikasi kalkulus diferensial meliputi perhitungan kecepatan dan percepatan, kemiringan suatu kurva, dan optimalisasi. Aplikasi dari kalkulus integral meliputi perhitungan luas, volume, panjang busur, pusat massa, kerja, dan tekanan. Aplikasi lebih jauh meliputi deret pangkat dan deret Fourier.^[14]

Kalkulus juga digunakan untuk mendapatkan pemahaman yang lebih rinci mengenai ruang, waktu, dan gerak. Selama berabad-abad, para matematikawan dan filsuf berusaha memecahkan paradoks yang meliputi pembagian bilangan dengan nol ataupun jumlah dari deret takterhingga. Seorang filsuf Yunani kuno memberikan beberapa contoh terkenal seperti paradoks Zeno. Kalkulus memberikan solusi, terutama di bidang limit dan deret takterhingga, yang kemudian berhasil memecahkan paradoks tersebut.^[14]

Prinsip dasar

Limit dan kecil tak terhingga

Kalkulus pada umumnya dikembangkan dengan memanipulasi sejumlah kuantitas yang sangat kecil. Objek ini, yang dapat diperlakukan sebagai angka, adalah sangat kecil. Sebuah bilangan dx yang kecilnya tak terhingga dapat lebih besar daripada 0, namun lebih kecil daripada bilangan apapun pada deret 1, 12, 13, ... dan bilangan real positif apapun. Setiap perkalian dengan kecil tak terhingga (infinitesimal) tetaplah kecil tak terhingga, dengan kata lain kecil tak terhingga tidak memenuhi "ciri-ciri Archimedes". Dari sudut pandang ini, kalkulus adalah sekumpulan teknik untuk memanipulasi kecil tak terhingga.^[17]

Pada abad ke-19, konsep kecil tak terhingga ini ditinggalkan karena tidak cukup cermat, sebaliknya ia digantikan oleh konsep limit (matematika). Limit menjelaskan nilai suatu fungsi pada nilai input tertentu dengan hasil dari nilai input terdekat. Dari sudut pandang ini, kalkulus adalah sekumpulan teknik memanipulasi limit-limit tertentu.^[17] Secara cermat, definisi limit suatu fungsi adalah:

Diberikan fungsi $f(x)$ yang didefinisikan pada interval di $p$ , terkecuali mungkin pada $p$ itu sendiri. Ketika $x$ mendekati $p$ , maka limit $f(x)$ dapat dikatakan mendekati $L$ , dan dituliskan sebagai:
$\lim _{x\to p}{f(x)}=L$

jika, untuk setiap bilangan $\varepsilon >0$ , terdapat bilangan $\delta >0$ yang berkoresponden dengannya sedemikian rupa untuk setiap $x$ :

$0<|x-p|<\delta \Longrightarrow |f(x)-L|<\varepsilon \,$

Turunan

Turunan dari suatu fungsi mewakili perubahan yang sangat kecil dari fungsi tersebut terhadap variabelnya. Proses menemukan turunan dari suatu fungsi disebut sebagai pendiferensialan ataupun diferensiasi.^[1]

Secara matematis, turunan fungsi $f(x)$ terhadap variabel $x$ adalah $f'$ yang nilainya pada titik $x$ adalah:

f'(x)=\lim _{h\to 0}{f(x+h)-f(x) \over {h}}

,

dengan syarat limit tersebut ada. Jika $f'$ ada pada titik $x$ tertentu, maka $f'$ dapat dikatakan terdiferensialkan (memiliki turunan) pada $x$ , dan jika $f'$ ada di setiap titik pada domain $f$ , maka $f$ dapat disebut terdiferensialkan.

Jika $z=x+h$ , $h=z-x$ , dan $h$ mendekati 0 jika dan hanya jika $z$ mendekati $x$ , maka definisi turunan di atas dapat ditulis pula sebagai:

f'(x)=\lim _{z\to x}{f(z)-f(x) \over {z-x}}

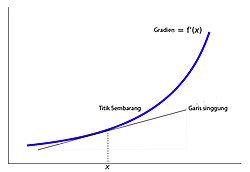
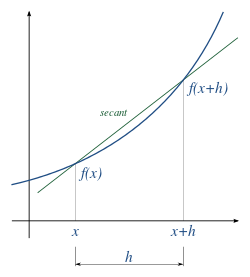
Perhatikan bahwa ekspresi ${f(x+h)-f(x) \over {h}}$ pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik $(x,f(x))$ dan $(x+h,f(x))$ pada kurva $f(x)$ . Ketika limit $h$ mendekati 0, maka kemiringan dari garis singgung yang diperoleh menyinggung kurva $f(x)$ pada titik $x$ . Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi $f(x)$ merupakan gradien dari fungsi tersebut.^[1]

Sebagai contoh, untuk menemukan gradien dari fungsi $f(x)=x^{2}$ pada titik (3,9):

{\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-9 \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}

Ilmu yang mempelajari definisi, sifat, dan aplikasi dari turunan atau kemiringan dari sebuah grafik disebut kalkulus diferensial

Garis singgung sebagai limit dari garis sekan. Turunan dari kurva $f(x)$ di suatu titik adalah kemiringan dari garis singgung yang menyinggung kurva pada titik tersebut. Kemiringan ini ditentukan dengan memakai nilai limit dari kemiringan garis sekan.

Notasi pendiferensialan

Terdapat berbagai macam notasi matematika yang dapat digunakan untuk menyatakan turunan, meliputi notasi Leibniz, notasi Lagrange, notasi Newton, dan notasi Euler.^[1]

Notasi Leibniz diperkenalkan oleh Gottfried Leibniz dan merupakan salah satu notasi yang paling awal digunakan. Ia sering digunakan terutama ketika hubungan antar $y=f(x)$ dipandang sebagai hubungan fungsional antara variabel bebas dengan variabel terikat. Turunan dari fungsi tersebut terhadap $x$ ditulis sebagai:^[15]

{\frac {dy}{dx}},\quad {\frac {df}{dx}}(x),

ataupun

{\frac {d}{dx}}f(x).

Notasi Lagrange diperkenalkan oleh Joseph Louis Lagrange dan merupakan notasi yang paling sering digunakan. Dalam notasi ini, turunan fungsi $f(x)$ ditulis sebagai $f'(x)$ ataupun hanya $f'$ .

Notasi Newton, juga disebut sebagai notasi titik, menempatkan titik di atas fungsi untuk menandakan turunan. Jika $y=f(t)$ , maka ${\dot {y}}$ mewakili turunan $y$ terhadap $t$ . Notasi ini hampir secara eksklusif digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang fisika dan bidang matematika yang berhubungan dengan fisika.

Notasi Euler menggunakan operator diferensial $D$ yang diterapkan pada fungsi $f$ untuk memberikan turunan pertamanya $Df$ . Jika $y=f(x)$ adalah variabel terikat, maka $x$ seringkali dilekatkan pada $x$ untuk mengklarifikasikan keterbebasan variabel $x$ Notasi Euler kemudian ditulis sebagai:

D_{x}y\,

atau

D_{x}f(x)\,

.

Notasi Euler ini sering digunakan dalam menyelesaikan persamaan diferensial linear.

	Notasi Leibniz	Notasi Lagrange	Notasi Newton	Notasi Euler
Turunan $f(x)$ terhadap $x$	${\frac {d}{dx}}f(x)$	$f'(x)$	${\dot {y}}$ dengan $y=f(x)$	$D_{x}f(x)\,$

Integral

Integral merupakan suatu objek matematika yang dapat diinterpretasikan sebagai luas wilayah ataupun generalisasi suatu wilayah. Proses menemukan integral suatu fungsi disebut sebagai pengintegralan ataupun integrasi. Integral dibagi menjadi dua, yaitu: integral tertentu dan integral tak tentu. Notasi matematika yang digunakan untuk menyatakan integral adalah $\int \,$ , seperti huruf S yang memanjang (S singkatan dari "Sum" yang berarti penjumlahan).^[1]

Integral tertentu

Diberikan suatu fungsi $f$ bervariabel real $x$ dan interval antara $[a,b]$ pada garis real, integral tertentu:

\int _{a}^{b}f(x)\,dx\,,

secara informal didefinisikan sebagai luas daerah pada bidang- $xy$ yang dibatasi oleh kurva grafik $f$ , sumbu- $x$ , dan garis vertikal $x=a$ dan $x=b$ .

Pada notasi integral di atas: $a$ adalah batas bawah dan $b$ adalah batas atas yang menentukan domain pengintegralan, $f$ adalah integran yang akan dievaluasi terhadap $x$ pada interval $[a,b]$ , dan $dx$ adalah variabel pengintegralan.

Seiring dengan semakin banyaknya subinterval dan semakin sempitnya lebar subinterval yang diambil, luas keseluruhan batangan akan semakin mendekati luas daerah di bawah kurva.

Terdapat berbagai jenis pendefinisian formal integral tertentu, namun yang paling umumnya digunakan adalah definisi integral Riemann. Integral Riemann didefinisikan sebagai limit dari "penjumlahan Riemann". Misalkan ingin mencari luas daerah yang dibatasi oleh fungsi $f$ pada interval tertutup $[a,b]$ . Dalam mencari luas daerah tersebut, interval $[a,b]$ dapat dibagi menjadi banyak subinterval yang lebarnya tidak perlu sama, dan memilih sejumlah $n-1$ titik $\{x_{1},x_{2},x_{3},\dots ,x_{n-1}\}$ antara $a$ dengan $b$ sehingga memenuhi hubungan:^[18]

a=x_{0}\leq x_{1}\leq x_{2}\leq \cdots \leq x_{n-1}\leq x_{n}=b.\,\!

Himpunan $P=\{x_{0},x_{1},x_{2},\ldots ,x_{n-1},x_{n}\}\,$ tersebut dapat dikatakan sebagai partisi $[a,b]$ , yang membagi $[a,b]$ menjadi sejumlah $n$ subinterval $[x_{0},x_{1}],[x_{1},x_{2}],\ldots ,[x_{n-1},x_{n}]$ . Lebar subinterval pertama $[x_{0},x_{1}]$ dinyatakan sebagai $\Delta x_{1}$ , demikian pula lebar subinterval ke-i dinyatakan sebagai $\Delta x_{i}=x_{i}-x_{i-1}$ . Pada tiap-tiap subinterval inilah dipilih suatu titik sembarang, dan pada subinterval ke- $i$ tersebut dipilih titik sembarang $t_{i}$ . Maka pada tiap-tiap subinterval akan terdapat batangan persegi panjang yang lebarnya sebesar $\Delta x$ dan tingginya berawal dari sumbu $x$ sampai menyentuh titik $(t_{i},f(t_{i}))$ pada kurva. Jika luas tiap-tiap batangan tersebut dihitung dengan mengalikan ƒ(t_i)· Δx_i dan menjumlahkan keseluruhan luas daerah batangan tersebut, maka akan didapatkan:

S_{p}=\sum _{i=1}^{n}f(t_{i})\Delta x_{i}

Penjumlahan $S_{p}$ disebut sebagai penjumlahan Riemann untuk $f$ pada interval $[a,b]$ . Perhatikan bahwa semakin kecil subinterval partisi yang diambil, hasil penjumlahan Riemann ini akan semakin mendekati nilai luas daerah yang diinginkan. Jika limit dari norma partisi $\lVert P\rVert$ mendekati nol, maka didapatkan luas daerah tersebut.^[18]

Secara cermat, definisi integral tertentu sebagai limit dari penjumlahan Riemann adalah:^[18]

Diberikan $f(x)$ sebagai fungsi yang terdefinisikan pada interval tertutup $[a,b]$ . Bilangan $I$ dikatakan sebagai integral tertentu $f$ di sepanjang $[a,b]$ dan bahwa $I$ adalah limit dari penjumlahan Riemann $\sum _{i=1}^{n}f(t_{i})\Delta x_{i}$ jikamemenuhi syarat berikut: Untuk setiap bilangan $\varepsilon >0$ , terdapat sebuah bilangan $\delta >0$ yang berkorespondensi dengannya sedemikian rupa untuk setiap partisi $P=\{x_{0},x_{1},\ldots ,x_{n}\}$ di sepanjang $[a,b]$ dengan $\lVert P\rVert <\delta$ dan pilihan $t_{i}$ apapun pada $[x_{k-1},t_{i}]$ , maka didapatkan
$\left|\sum _{i=1}^{n}f(t_{i})\Delta x_{i}-I\right|<\varepsilon .$

Secara matematis dapat ditulis:

\lim _{\lVert P\rVert \to 0}\sum _{i=1}^{n}f(t_{i})\Delta x_{i}=I=\int _{a}^{b}f(x)\,dx

Jika masing-masing partisi mempunyai sejumlah $n$ subinterval yang sama, maka lebar $\Delta x={\tfrac {b-a}{n}}$ , sehingga persamaan di atas dapat pula ditulis sebagai:

\lim _{n\to \infty }\sum _{i=1}^{n}f(t_{i})\Delta x=I=\int _{a}^{b}f(x)\,dx

Limit ini selalu diambil ketika norma partisi mendekati nol dan jumlah subinterval yang ada mendekati tak terhingga banyaknya.^[18]

Contoh

Sebagai contoh, jika integral tertentu $\int _{0}^{b}x\,dx$ dihitung untuk mencari luas daerah $A$ di bawah kurva $y=x$ pada interval $[0,b]$ , $b>0$ , maka perhitungan integral tertentu $\int _{0}^{b}x\,dx$ sebagai limit dari penjumlahan Riemannnya adalah $\lim _{\lVert P\rVert \to 0}\sum _{i=1}^{n}f(t_{i})\Delta x_{i}$

Pemilihan partisi ataupun titik $t_{i}$ secara sembarang akan menghasilkan nilai yang sama sepanjang norma partisi tersebut mendekati nol. Jika partisi $P$ yang dipilih membagi-bagi interval $[0,b]$ menjadi $n$ subinterval yang berlebar sama $\Delta x={\tfrac {b-0}{n}}={\tfrac {b}{n}}$ dan titik $t_{i}$ yang dipilih adalah titik akhir kiri setiap subinterval, partisi yang didapatkan adalah $P=\{0,{\tfrac {b}{n}},{\tfrac {2b}{n}},{\tfrac {3b}{n}},\ldots ,{\tfrac {nb}{n}}\}$ dan $t_{i}={\tfrac {ib}{n}}$ , sehingga:

{\begin{aligned}\int _{0}^{b}f(x)\,dx&=\lim _{n\to \infty }\sum _{i=1}^{n}f(t_{i})\Delta x\\&=\lim _{n\to \infty }\sum _{i=1}^{n}{\frac {ib}{n}}.{\frac {b}{n}}\\&=\lim _{n\to \infty }\sum _{i=1}^{n}{\frac {ib^{2}}{n^{2}}}\\&=\lim _{n\to \infty }{\frac {b^{2}}{n^{2}}}\sum _{i=1}^{n}i\\&=\lim _{n\to \infty }{\frac {b^{2}}{n^{2}}}.{\frac {n(n+1)}{2}}\\&=\lim _{n\to \infty }{\frac {b^{2}}{2}}(1+{\frac {1}{n}})\\\end{aligned}}

Seiring dengan $n$ mendekati tak terhingga dan norma partisi $\lVert P\rVert$ mendekati 0, maka didapatkan:

\int _{0}^{b}f(x)\,dx=A={\frac {b^{2}}{2}}

Dalam praktiknya, penerapan definisi integral tertentu dalam mencari nilai integral tertentu tersebut jarang sekali digunakan karena tidak praktis. Teorema dasar kalkulus (lihat bagian bawah) memberikan cara yang lebih praktis dalam mencari nilai integral tertentu.^[1]

Integral tak tentu

Manakala integral tertentu adalah sebuah bilangan yang besarnya ditentukan dengan mengambil limit penjumlahan Riemann, yang diasosiasikan dengan partisi interval tertutup yang norma partisinya mendekati nol, teorema dasar kalkulus (lihat bagian bawah) menyatakan bahwa integral tertentu sebuah fungsi kontinu dapat dihitung dengan mudah jika antiturunan/antiderivatif fungsi tersebut dapat dicari melalui teorema berikut.^[1]

Jika
$F'\!(x)={\frac {d}{dx}}F(x)=f(x).$

maka keseluruhan himpunan antiturunan/antiderivatif sebuah fungsi $f$ adalah integral tak tentu ataupun primitif dari $f$ terhadap $x$ dan dituliskan secara matematis sebagai:

$\int f(x)dx=F(x)+C$

Bentuk $F(x)+C$ adalah antiderivatif umum $f$ dan $C$ adalah konstanta sembarang.

Misalkan terdapat sebuah fungsi $f(x)=x^{2}$ , maka integral tak tentu ataupun antiturunan dari fungsi tersebut adalah:

\int x^{2}dx={\frac {1}{3}}x^{3}+C

.

Perhatikan bahwa integral tertentu berbeda dengan integral tak tentu. Integral tertentu dalam bentuk $\int _{a}^{b}f(x)\,dx$ adalah sebuah bilangan, manakala integral tak tentu: $\int f(x)\,dx$ adalah sebuah fungsi yang memiliki tambahan konstanta sembarang $C$ .

Teorema dasar

Teorema dasar kalkulus menyatakan bahwa turunan dan integral adalah dua operasi yang saling berlawanan. Lebih tepatnya, teorema ini menghubungkan nilai dari anti derivatif dengan integral tertentu. Karena lebih mudah menghitung sebuah anti derivatif daripada menerapkan definisi integral tertentu, teorema dasar kalkulus memberikan cara yang praktis dalam menghitung integral tertentu.^[1]

Teorema dasar kalkulus menyatakan:

Jika sebuah fungsi $f$ adalah kontinu pada interval $[a,b]$ dan jika $F$ adalah fungsi yang mana turunannya adalah $f$ pada interval $(a,b)$ , maka
$\int _{a}^{b}f(x)\,dx=F(b)-F(a).$

Lebih lanjut, untuk setiap $x$ di interval $(a,b)$ ,

$F'(x)={\frac {d}{dx}}\int _{a}^{x}f(t)\,dt=f(x).$

Sebagai contoh, jika ingin menghitung nilai integral $\int _{a}^{b}x\,dx$ , daripada menggunakan definisi integral tertentu sebagai limit dari penjumlahan Riemann (lihat bagian atas), maka teorema dasar kalkulus dapat digunakan dalam menghitung nilai integral tersebut.

Antiderivatif dari fungsi $f(x)=x\,$ adalah $F(x)={\tfrac {1}{2}}x^{2}+C$ . Oleh sebab itu, menurut dengan teorema dasar kalkulus, nilai dari integral tertentu $\int _{a}^{b}x\,dx$ adalah:

{\begin{aligned}\int _{a}^{b}x\,dx&=F(b)-F(a)\\&={\frac {1}{2}}b^{2}-{\frac {1}{2}}a^{2}\\\end{aligned}}

Jika ingin mencari luas daerah $A$ terhadap kurva $y=x$ pada interval $[0,b]$ , $b>0$ , maka didapatkan:

\int _{0}^{b}x\,dx={\frac {b^{2}}{2}}

Perhatikan bahwa hasil yang didapatkan dengan menggunakan teorema dasar kalkulus ini adalah sama dengan hasil yang didapatkan dengan menerapkan definisi integral tertentu (lihat bagian atas). Oleh karena lebih praktis, teorema dasar kalkulus sering digunakan untuk mencari nilai integral tertentu.^[1]

Aplikasi

Pola spiral logaritma cangkang Nautilus adalah contoh klasik untuk menggambarkan perkembangan dan perubahan yang berkaitan dengan kalkulus.

Kalkulus digunakan di setiap cabang sains fisik, sains komputer, statistika, teknik, ekonomi, bisnis, kedokteran, kependudukan, dan di bidang-bidang lainnya. Setiap konsep di mekanika klasik saling berhubungan melalui kalkulus. Massa dari sebuah benda dengan massa jenis yang tidak diketahui, momen inersia dari suatu objek, dan total energi dari sebuah objek dapat ditentukan dengan menggunakan kalkulus.^[1]

Dalam subdisiplin listrik dan magnetisme, kalkulus dapat digunakan untuk mencari total aliran (fluks) dari sebuah medan elektromagnetik. Contoh historis lainnya adalah penggunaan kalkulus di hukum gerak Newton, dinyatakan sebagai laju perubahan yang merujuk pada turunan: Laju perubahan momentum dari sebuah benda adalah sama dengan resultan gaya yang bekerja pada benda tersebut dengan arah yang sama.^[1]

Bahkan rumus umum dari hukum kedua Newton: Gaya = Massa × Percepatan, menggunakan perumusan kalkulus diferensial karena percepatan bisa dinyatakan sebagai turunan dari kecepatan. Teori elektromagnetik Maxwell dan teori relativitas Einstein juga dirumuskan menggunakan kalkulus diferensial.^[1]

Lihat pula

Referensi

^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m Latorre, Donald R.; Kenelly, John W.; Reed, Iris B.; Biggers, Sherry (2007), Calculus Concepts: An Applied Approach to the Mathematics of Change, Cengage Learning, hlm. 2, ISBN 0-618-78981-2, diarsipkan dari versi asli tanggal 2023-03-27, diakses tanggal 2013-11-08 , Chapter 1, p 2 Diarsipkan 2023-03-27 di Wayback Machine.
^ Morris Kline, Mathematical thought from ancient to modern times, Vol. I
^ Helmer Aslaksen. Why Calculus? Diarsipkan 2010-10-14 di Wayback Machine. National University of Singapore.
^ Archimedes, Method, in The Works of Archimedes ISBN 978-0-521-66160-7
^ "Aryabhata the Elder". Diarsipkan dari versi asli tanggal 2015-07-11. Diakses tanggal 2007-08-09.
^ Ian G. Pearce. Bhaskaracharya II. Diarsipkan 2016-09-01 di Wayback Machine.
^ Victor J. Katz (1995). "Ideas of Calculus in Islam and India", Mathematics Magazine 68 (3), hlm. 163-174.
^ J. L. Berggren (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat", Journal of the American Oriental Society 110 (2), hlm. 304-309.
^ "Madhava". Biography of Madhava. School of Mathematics and Statistics University of St Andrews, Scotland. Diarsipkan dari versi asli tanggal 2006-05-14. Diakses tanggal 2006-09-13.
^ "An overview of Indian mathematics". Indian Maths. School of Mathematics and Statistics University of St Andrews, Scotland. Diarsipkan dari versi asli tanggal 2006-07-03. Diakses tanggal 2006-07-07.
^ "Science and technology in free India" (PDF). Government of Kerala — Kerala Call, September 2004. Prof.C.G.Ramachandran Nair. Diarsipkan dari versi asli (PDF) tanggal 2006-08-21. Diakses tanggal 2006-07-09.
^ Charles Whish (1835). Transactions of the Royal Asiatic Society of Great Britain and Ireland.
^ The geometrical lectures of Isaac Barrow, translated, with notes and proofs, and a discussion on the advance made therein on the work of his predecessors in the infinitesimal calculus. Chicago: Open Court. 1916.
^ ^a ^b ^c ^d ^e Simmons, George F. (2007). Calculus Gems: Brief Lives and Memorable Mathematics. Mathematical Association of America. hlm. 98. ISBN 0-88385-561-5.
^ ^a ^b ^c Leibniz, Gottfried Wilhelm. The Early Mathematical Manuscripts of Leibniz. Cosimo, Inc., 2008. hlm. 228. Online Copy
^ Unlu, Elif (1995). "Maria Gaetana Agnesi". Agnes Scott College. Diarsipkan dari versi asli tanggal 1998-12-03. Diakses tanggal 2013-11-08.
^ ^a ^b Larson, Ron; Edwards, Bruce H. (2010). Calculus of a single variable (edisi ke-Ninth). Brooks/Cole, Cengage Learning. ISBN 978-0-547-20998-2.
^ ^a ^b ^c ^d Bernard Riemann. "Über die Darstellbarkeit einer Function durch eine trigonometrische Reihe" (On the representability of a function by a trigonometric series; i.e., when can a function be represented by a trigonometric series). Makalah ini diserahkan kepada Universitas Göttingen pada tahun 1854 sebagai Habilitationsschrift Riemann (kualifikasi untuk menjadi instruktur). Diterbitkan pada tahun 1868 dalam Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen (Proceedings of the Royal Philosophical Society at Göttingen), vol. 13, hlm. 87-132. (dapat dibaca di sini Diarsipkan 2023-03-27 di Wayback Machine..) Definisi integral Riemann, lihat bagian 4, "Über der Begriff eines bestimmten Integrals und den Umfang seiner Gültigkeit" (On the concept of a definite integral and the extent of its validity), hlm. 101-103.

Daftar pustaka

Donald A. McQuarrie (2003). Mathematical Methods for Scientists and Engineers, University Science Books. ISBN 978-1-891389-24-5
James Stewart (2002). Calculus: Early Transcendentals, 5th ed., Brooks Cole. ISBN 978-0-534-39321-2

Sumber lain

Bacaan lebih lanjut

Robert A. Adams. (1999) ISBN 978-0-201-39607-2 Calculus: A complete course.
Albers, Donald J.; Richard D. Anderson and Don O. Loftsgaarden, ed. (1986) Undergraduate Programs in the Mathematics and Computer Sciences: The 1985-1986 Survei, Mathematical Association of America No. 7,
John L. Bell: A Primer of Infinitesimal Analysis, Cambridge University Press, 1998. ISBN 978-0-521-62401-5.
Florian Cajori, "The History of Notations of the Calculus." Annals of Mathematics, 2nd Ser., Vol. 25, No. 1 (Sep., 1923), hlm. 1-46.
Leonid P. Lebedev and Michael J. Cloud: "Approximating Perfection: a Mathematician's Journey into the World of Mechanics, Ch. 1: The Tools of Calculus", Princeton Univ. Press, 2004
Cliff Pickover. (2003) ISBN 978-0-471-26987-8 Calculus and Pizza: A Math Cookbook for the Hungry Mind.
Michael Spivak. (Sept 1994) ISBN 978-0-914098-89-8 Calculus. Publish or Perish publishing.
Silvanus P. Thompson dan Martin Gardner. (1998) ISBN 978-0-312-18548-0 Calculus Made Easy.
Mathematical Association of America. (1988) Calculus for a New Century; A Pump, Not a Filter, The Association, Stony Brook, NY. ED 300 252.
Thomas/Finney. (1996) ISBN 978-0-201-53174-9 Calculus and Analytic geometry 9th, Addison Wesley.
Weisstein, Eric W. "Second Fundamental Theorem of Calculus." dari MathWorld—A Wolfram Web Resource.

Pustaka daring

Crowell, B., (2003). "Calculus" Light and Matter, Fullerton. Retrieved 6th May 2007 from http://www.lightandmatter.com/calc/calc.pdf
Garrett, P., (2006). "Notes on first year calculus" University of Minnesota. Retrieved 6th May 2007 from http://www.math.umn.edu/~garrett/calculus/first_year/notes.pdf
Faraz, H., (2006). "Understanding Calculus" Retrieved Retrieved 6th May 2007 from Understanding Calculus, URL http://www.understandingcalculus.com/ (HTML only)
Keisler, H. J., (2000). "Elementary Calculus: An Approach Using Infinitesimals" Retrieved 6th May 2007 from http://www.math.wisc.edu/~keisler/keislercalc1.pdf
Mauch, S. (2004). "Sean's Applied Math Book" California Institute of Technology. Retrieved 6th May 2007 from http://www.cacr.caltech.edu/~sean/applied_math.pdf Diarsipkan 2007-06-14 di Wayback Machine.
Sloughter, Dan., (2000) "Difference Equations to Differential Equations: An introduction to calculus". Retrieved 6th May 2007 from http://math.furman.edu/~dcs/book/
Stroyan, K.D., (2004). "A brief introduction to infinitesimal calculus" University of Iowa. Retrieved 6th May 2007 from http://www.math.uiowa.edu/~stroyan/InfsmlCalculus/InfsmlCalc.htm Diarsipkan 2005-09-11 di Wayback Machine. (HTML only)
Strang, G. (1991) "Calculus" Massachusetts Institute of Technology. Retrieved 6th May 2007 from http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm.

Halaman web

Calculus.org: The Calculus page di Universitas California, Davis
COW: Calculus on the Web di Universitas Temple
Online Integrator (WebMathematica) dari Wolfram Research
The Role of Calculus in College Mathematics Diarsipkan 2021-07-26 di Wayback Machine. dari ERICDigests.org
OpenCourseWare Calculus Diarsipkan 2010-05-05 di Wayback Machine. dari Institut Teknologi Massachusetts
Infinitesimal Calculus Encyclopaedia of Mathematics, Michiel Hazewinkel ed. .

[concepts-1] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m Latorre, Donald R.; Kenelly, John W.; Reed, Iris B.; Biggers, Sherry (2007), Calculus Concepts: An Applied Approach to the Mathematics of Change, Cengage Learning, hlm. 2, ISBN 0-618-78981-2, diarsipkan dari versi asli tanggal 2023-03-27, diakses tanggal 2013-11-08 , Chapter 1, p 2 Diarsipkan 2023-03-27 di Wayback Machine.

[2] Morris Kline, Mathematical thought from ancient to modern times, Vol. I

[Aslaksen-3] Helmer Aslaksen. Why Calculus? Diarsipkan 2010-10-14 di Wayback Machine. National University of Singapore.

[4] Archimedes, Method, in The Works of Archimedes ISBN 978-0-521-66160-7

[5] "Aryabhata the Elder". Diarsipkan dari versi asli tanggal 2015-07-11. Diakses tanggal 2007-08-09.

[6] Ian G. Pearce. Bhaskaracharya II. Diarsipkan 2016-09-01 di Wayback Machine.

[7] Victor J. Katz (1995). "Ideas of Calculus in Islam and India", Mathematics Magazine 68 (3), hlm. 163-174.

[8] J. L. Berggren (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat", Journal of the American Oriental Society 110 (2), hlm. 304-309.

[madhava-9] "Madhava". Biography of Madhava. School of Mathematics and Statistics University of St Andrews, Scotland. Diarsipkan dari versi asli tanggal 2006-05-14. Diakses tanggal 2006-09-13.

[scotlnd-10] "An overview of Indian mathematics". Indian Maths. School of Mathematics and Statistics University of St Andrews, Scotland. Diarsipkan dari versi asli tanggal 2006-07-03. Diakses tanggal 2006-07-07.

[pdffile3-11] "Science and technology in free India" (PDF). Government of Kerala — Kerala Call, September 2004. Prof.C.G.Ramachandran Nair. Diarsipkan dari versi asli (PDF) tanggal 2006-08-21. Diakses tanggal 2006-07-09.

[charles-12] Charles Whish (1835). Transactions of the Royal Asiatic Society of Great Britain and Ireland.

[13] The geometrical lectures of Isaac Barrow, translated, with notes and proofs, and a discussion on the advance made therein on the work of his predecessors in the infinitesimal calculus. Chicago: Open Court. 1916.

[Simmons-14] Simmons, George F. (2007). Calculus Gems: Brief Lives and Memorable Mathematics. Mathematical Association of America. hlm. 98. ISBN 0-88385-561-5.

[leibniz-15] Leibniz, Gottfried Wilhelm. The Early Mathematical Manuscripts of Leibniz. Cosimo, Inc., 2008. hlm. 228. Online Copy

[16] Unlu, Elif (1995). "Maria Gaetana Agnesi". Agnes Scott College. Diarsipkan dari versi asli tanggal 1998-12-03. Diakses tanggal 2013-11-08.

[Larson-17] Larson, Ron; Edwards, Bruce H. (2010). Calculus of a single variable (edisi ke-Ninth). Brooks/Cole, Cengage Learning. ISBN 978-0-547-20998-2.

[riemann-18] Bernard Riemann. "Über die Darstellbarkeit einer Function durch eine trigonometrische Reihe" (On the representability of a function by a trigonometric series; i.e., when can a function be represented by a trigonometric series). Makalah ini diserahkan kepada Universitas Göttingen pada tahun 1854 sebagai Habilitationsschrift Riemann (kualifikasi untuk menjadi instruktur). Diterbitkan pada tahun 1868 dalam Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen (Proceedings of the Royal Philosophical Society at Göttingen), vol. 13, hlm. 87-132. (dapat dibaca di sini Diarsipkan 2023-03-27 di Wayback Machine..) Definisi integral Riemann, lihat bagian 4, "Über der Begriff eines bestimmten Integrals und den Umfang seiner Gültigkeit" (On the concept of a definite integral and the extent of its validity), hlm. 101-103.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

l b s Matematika (Bidang matematika)
Fondasi	Filsafat matematika Logika matematika Teori himpunan Teori informasi Teori kategori Teori tipe
Aljabar	Abstrak Elementer Homologis Komutatif Linear Multilinear Universal Teori grup Teori representasi
Analisis	Kalkulus Analisis fungsional Analisis harmonik Analisis kompleks Analisis real Persamaan diferensial Teori ukuran Teori sistem dinamis
Diskret	Kombinatorika Teori graf Teori order
Geometri	Aljabar Analitis Diferensial Diskrit Euklides Hingga Trigonometri
Komputasi	Analisis numerik (Topik) Ilmu komputer Komputasi simbolik Teori komputasi Teori kompleksitas komputasi Optimisasi matematika
Teori bilangan	Aritmetika Geometri Diophantine Teori bilangan aljabar Teori bilangan analitis
Topologi	Teori homotopi Aljabar Diferensial Geometris Umum
Terapan	Matematika biologi Matematika ekonomi Matematika keuangan Fisika matematis Kimia matematika Psikologi matematis Statistika Statistika matematika Teori peluang Ilmu sistem (Teori kendali, Teori permainan, Riset operasi)
Divisi	Matematika murni Matematika terapan Matematika diskret Matematika komputasi
Topik terkait	Matematika dan seni Matematika rekreasi Pendidikan matematika Sejarah matematika
Kategori Portal matematika Kerangka Daftar