Logaritma: Perbedaan antara revisi
Taman kodok (bicara | kontrib) →Kalkulus: tambah dikit lagi |
Fitur saranan suntingan: 3 pranala ditambahkan. |
||
| (424 revisi antara oleh lebih dari 100 100 pengguna tak ditampilkan) | |||
| Baris 1: | Baris 1: | ||
[[Berkas:Logarithm plots.png|jmpl|300x300px|Grafik fungsi logaritma dengan tiga bilangan pokok yang umum. Titik khusus {{math|<sup>''b''</sup>log ''b'' {{=}} 1}} diperlihatkan oleh garis bertitik, dan semua kurva fungsi memotong di {{math|1=<sup>''b''</sup>log 1 = 0}}.]]{{Operasi aritmetika}} |
|||
[[Gambar:Logarithms.png|thumb|300px|Grafik logaritma terhadap basis yang berbeda. <span style="color:red">merah</span> adalah terhadap basis e, <span style="color:green">hijau</span> adalah terhadap basis 10, dan <span style="color:purple">ungu</span> adalah terhadap basis 1.7. Perhatikan bahwa grafik logaritma terhadap basis yang berbeda selalu melewati titik (1,0)]] |
|||
Dalam [[matematika]], '''logaritma''' adalah [[fungsi invers]] dari [[eksponensiasi]]. Dengan kata lain, logaritma dari {{mvar|x}} adalah [[eksponen]] dengan [[bilangan pokok]] {{mvar|b}} yang dipangkatkan dengan bilangan konstan lain agar memperoleh nilai {{mvar|x}}. Kasus sederhana dalam logaritma adalah menghitung jumlah munculnya faktor yang sama dalam perkalian berulang. Sebagai contoh, {{math|1000 {{=}} 10 × 10 × 10 {{=}} 10<sup>3</sup>}} dibaca, "logaritma 1000 dengan bilangan pokok 10 sama dengan 3" atau dinotasikan sebagai {{math|<sup>10</sup>log (1000) {{=}} 3}}. Logaritma dari {{mvar|x}} dengan ''bilangan pokok'' {{mvar|b}} dilambangkan {{math|<sup>''b''</sup>log ''x''}}. Terkadang logaritma dilambangkan sebagai {{math|log<sub>''b''</sub> (''x'')}} atau tanpa menggunakan tanda kurung, {{math|log<sub>''b''</sub> ''x''}}, atau bahkan tanpa menggunakan bilangan pokok khusus, {{math|log ''x''}}. |
|||
'''Logaritma''' adalah operasi [[matematika]] yang merupakan kebalikan dari eksponen atau [[pemangkatan]]. |
|||
Ada tiga bilangan pokok logaritma yang umum beserta kegunaannya. Logaritma dengan bilangan pokok {{math|10}} ({{math|1=''b'' = 10}}) disebut sebagai [[logaritma umum]], yang biasanya dipakai dalam ilmu sains dan rekayasa. Logaritma dengan dengan bilangan pokok [[E (konstanta matematika)|bilangan {{Math|''e''}}]] ({{math|''b'' ≈ 2.718}}) disebut sebagai [[logaritma alami]], yang dipakai dengan luas dalam matematika dan fisika, karena dapat mempermudah perhitungan [[integral]] dan [[turunan]]. Logaritma dengan bilangan pokok {{math|2}} ({{math|1=''b'' = 2}}) disebut sebagai [[logaritma biner]], yang seringkali dipakai dalam [[ilmu komputer]]. |
|||
Rumus dasar logaritma: |
|||
Logaritma diperkenalkan oleh [[John Napier]] pada tahun 1614 sebagai alat yang menyederhanakan perhitungan.<ref>{{citation|url=http://archive.org/details/johnnapierinvent00hobsiala|title=John Napier and the invention of logarithms, 1614; a lecture|last=Hobson|first=Ernest William|date=1914|publisher=Cambridge : University Press|others=University of California Libraries}}</ref> Logaritma dipakai lebih cepat dalam navigator, ilmu sains, rekayasa, ilmu ukur wilayah, dan bidang lainnya untuk lebih mempermudah perhitungan nilai yang sangat akurat. Dengan menggunakan [[Tabel matematika|tabel logaritma]], cara yang membosankan seperti mengalikan digit yang banyak dapat digantikan dengan melihat tabel dan penjumlahan yang lebih mudah. Ini dapat dilakukan karena logaritma dari [[Darab (matematika)|hasil kali]] bilangan merupakan logaritma dari [[Penjumlahan|jumlah]] faktor bilangan: |
|||
b<sup>c</sup>= a ditulis sebagai <sup>b</sup>log a = c (b disebut basis) |
|||
: <math> ^b\!\log(xy) = \, ^b\!\log x + \, ^b\!\log y,</math> |
|||
Beberapa orang menuliskan <sup>b</sup>log a = c sebagai log<sub>b</sub>a = c. |
|||
asalkan bahwa {{mvar|b}}, {{mvar|x}} dan {{mvar|y}} bilangan positif dan {{math|''b'' ≠ 1}}. [[Mistar hitung]] yang juga berasal dari logaritma dapat mempermudah perhitungan tanpa menggunakan tabel, namun perhitungannya kurang akurat. [[Leonhard Euler]] mengaitkan gagasan logaritma saat ini dengan [[fungsi eksponensial]] pada abad ke-18, dan juga memperkenalkan huruf {{mvar|e}} sebagai bilangan pokok dari logaritma alami.<ref>{{citation|title=Theory of complex functions|last=Remmert, Reinhold.|date=1991|publisher=Springer-Verlag|isbn=0387971955|location=New York|oclc=21118309}}</ref> |
|||
== Basis == |
|||
Penerapan [[skala logaritmik]] dipakai dalam mengurangi kuantitas yang sangat besar menjadi lebih kecil. Sebagai contoh, [[desibel]] (dB) adalah [[satuan]] yang digunakan untuk menyatakan [[Tingkat (kuantitas logaritmik)|rasio sebagai logaritma]], sebagian besar untuk kekuatan sinyal dan amplitudo (contoh umumnya pada [[tekanan suara]]). Dalam kimia, [[pH]] mengukur [[Asam|keasaman]] dari [[larutan berair]] melalui logaritma. Logaritma umumnya dipakai dalam [[rumus]] ilmiah, dalam pengukuran [[Teori kompleksitas komputasi|kompleksitas algoritma]] dan objek geometris yang disebut sebagai [[fraktal]]. Logaritma juga membantu untuk menjelaskan [[frekuensi]] rasio [[Interval (musik)|interval musik]], ditemukan di rumus yang menghitung [[bilangan prima]] atau [[Hampiran Stirling|hampiran]] [[faktorial]], memberikan gambaran dalam [[psikofisika]], dan dapat membantu perhitungan [[akuntansi forensik]]. |
|||
Basis yang sering dipakai atau paling banyak dipakai adalah basis 10, e≈ 2.71828... dan 2. |
|||
Konsep logaritma sebagai invers dari eksponensiasi juga memperluas ke struktur matematika lain. Namun pada umumnya, logaritma cenderung merupakan fungsi bernilai banyak. Sebagai contoh, [[logaritma kompleks]] merupakan [[Fungsi invers|invers]] dari fungsi eksponensial pada [[bilangan kompleks]]. Mirip dengan contoh sebelumnya, [[logaritma diskret]] dalam grup hingga, merupakan invers fungsi eksponensial bernilai banyak yang memiliki kegunaan dalam [[kriptografi kunci publik]]. |
|||
== Notasi == |
|||
== Alasan == |
|||
*Di Indonesia, kebanyakan buku pelajaran Matematika menggunakan notasi <sup>b</sup>log a daripada log<sub>b</sub>a. Buku-buku Matematika berbahasa Inggris menggunakan notasi log<sub>b</sub>a |
|||
[[Berkas:Binary logarithm plot with grid.png|right|thumb|upright=1.35|alt=Grafik memperlihatkan kurva logaritmik yang memotong\ sumbu-''x'' di {{math|''x''= 1}} dan mendekati negatif takhingga di sepanjang garis sumbu-''y''.|ka|jmpl|Gambar memperlihatkan [[Grafik fungsi|grafik]] logaritma dengan bilangan pokok 2 memotong [[Sistem koordinat Cartesius|sumbu-''x'']] di {{math|''x'' {{=}} 1}} dan melalui titik {{nowrap|(2, 1)}}, {{nowrap|(4, 2)}}, dan {{nowrap|(8, 3)}}, sebagai contoh, {{math|log<sub>2</sub>(8) {{=}} 3}} dan {{math|2<sup>3</sup> {{=}} 8}}. Grafik tersebut dengan sembarang mendekati sumbu-{{mvar|y}}, namun [[Asimtot|tidak mendekati sumbu-''x'']].]] |
|||
*Beberapa orang menulis ''ln a'' sebagai ganti ''<sup>e</sup>log a'', ''log a'' sebagai ganti ''<sup>10</sup>log a'' dan ''ld a'' sebagai ganti ''<sup>2</sup>log a''. |
|||
Operasi aritmetika yang paling dasar adalah [[penambahan]], [[perkalian]], dan [[Eksponensiasi|eksponen]]. Kebalikan dari penambahan adalah [[pengurangan]], dan kebalikan dari perkalian adalah [[pembagian]]. Mirip dengan contoh sebelumnya, logaritma merupakan kebalikan (atau invers) dari operasi [[eksponensiasi]]. Eksponensiasi adalah bilangan ''bilangan pokok'' {{mvar|b}} yang ketika dipangkatkan dengan {{mvar|y}} memberikan nilai {{mvar|x}}. Ini dirumuskan sebagai |
|||
*Pada kebanyakan kalkulator, LOG menunjuk kepada logaritma berbasis 10 dan LN menunjuk kepada logaritma berbasis e. |
|||
*Pada beberapa bahasa pemrograman komputer seperti [[C]],[[C++]],[[Java]] dan [[BASIC]], LOG menunjuk kepada logaritma berbasis e. |
|||
*Terkadang Log x (huruf besar L) menunjuk kepada <sup>10</sup>log x dan log x (huruf kecil L) menunjuk kepada <sup>e</sup>log x. |
|||
: <math>b^y=x.</math> |
|||
== Mencari nilai logaritma == |
|||
Cara untuk mencari nilai logaritma antara lain dengan menggunakan: |
|||
*[[Tabel]] |
|||
*[[Kalkulator]] (yang sudah dilengkapi fitur log) |
|||
Sebagai contoh, {{math|2}} pangkat {{math|3}} memberikan nilai {{math|8}}. Secara matematis, <math>2^3 = 8</math>. |
|||
== Rumus == |
|||
*<sup>x</sup>log x = 1 |
|||
*<sup>x^n</sup>log x<sup>m</sup> = m/n |
|||
*<sup>b</sup>log x + <sup>b</sup>log y = <sup>b</sup>log (x.y) |
|||
*<sup>b</sup>log x - <sup>b</sup>log y = <sup>b</sup>log (x:y) |
|||
*(<sup>a</sup>log b)(<sup>b</sup>log c) = <sup>a</sup>log c |
|||
*<sup>b</sup> log x<sup>n</sup> = n.<sup>b</sup>log x |
|||
*<sup>b</sup> log x = <sup>k</sup>log x : <sup>k</sup>log b |
|||
Logaritma dengan bilangan pokok {{mvar|b}} adalah operasi invers yang menyediakan nilai keluaran {{mvar|y}} dari nilai masukan {{mvar|x}}. Hal ini mengartikan bahwa {{math|1=''y'' = <sup>b</sup>log ''x''}} ekuivalen dengan {{math|1=''x'' = ''b''<sup>''y''</sup>}}, jika {{mvar|b}} [[bilangan real]] positif. (Jika {{mvar|b}} bukanlah bilangan real positif, eksponensiasi dan logaritma dapat terdefinisi tetapi membutuhkan beberapa nilai, sehingga definisi darinya semakin rumit.) |
|||
Salah satu alasan bersejarah utamanya dalam memperkenalkan logaritma adalah rumus |
|||
== Kegunaan logaritma == |
|||
Logaritma sering digunakan untuk memecahkan persamaan yang pangkatnya tidak diketahui. Turunannya mudah dicari dan karena itu logaritma sering digunakan sebagai solusi dari [[integral]]. Dalam persamaan ''b''<sup>''n''</sup> = ''x'', ''b'' dapat dicari dengan [[akar (matematika)|pengakaran]], ''n'' dengan logaritma, dan ''x'' dengan [[fungsi eksponensial]]. |
|||
: <math>^b\!\log(xy)= \,^b\!\log x + \,^b\!\log y,</math> |
|||
===Sains dan teknik=== |
|||
Dalam sains, terdapat banyak besaran yang umumnya diekspresikan dengan logaritma. Sebabnya, dan contoh-contoh yang lebih lengkap, dapat dilihat di [[skala logaritmik]]. |
|||
yang dapat mempermudah perhitungan nilai perkalian dan pembagian dengan penjumlahan, pengurangan, dan melihat [[tabel logaritma]]. Perhitungan ini dipakai sebelum komputer ditemukan. |
|||
* Negatif dari logaritma berbasis 10 digunakan dalam [[kimia]] untuk mengekspresikan [[konsentrasi]] ion hidronium ([[pH]]). Contohnya, konsentrasi ion hidronium pada [[air]] adalah 10<sup>−7</sup> pada suhu 25 °C, sehingga pH-nya 7. |
|||
== Definisi == |
|||
* Satuan ''bel'' (dengan simbol B) adalah satuan pengukur perbandingan (rasio), seperti perbandingan nilai [[daya]] dan [[tegangan]]. Kebanyakan digunakan dalam bidang [[telekomunikasi]], [[elektronik]], dan [[akustik]]. Salah satu sebab digunakannya logaritma adalah karena [[telinga]] manusia mempersepsikan suara yang terdengar secara logaritmik. Satuan Bel dinamakan untuk mengenang jasa [[Alexander Graham Bell]], seorang penemu di bidang telekomunikasi. Satuan [[desibel]] (dB), yang sama dengan 0.1 bel, lebih sering digunakan. |
|||
Diberikan [[bilangan real]] positif {{mvar|1=''b''}} sehingga {{math|1=''b'' ≠ 1}}, maka ''logaritma'' dari bilangan real positif {{mvar|x}} terhadap bilangan pokok {{mvar|b}}{{refn|Perbatasan {{mvar|x}} dan {{mvar|b}} dijelaskan pada bagian [[#Sifat analitik|"Sifat analitik"]].|group=nb}} adalah eksponen dengan bilangan pokok {{mvar|b}} yang dipangkatkan bilangan agar memperoleh nilai {{mvar|x}}. Dengan kata lain, logaritma bilangan pokok {{mvar|b}} dari {{mvar|x}} adalah bilangan real {{mvar|y}} sehingga {{math|1=''b''<sup>''y''</sup> = ''x''}}.<ref>{{Citation|last1=Kate|first1=S.K.|last2=Bhapkar|first2=H.R.|title=Basics Of Mathematics|location=Pune|publisher=Technical Publications|isbn=978-81-8431-755-8|year=2009|url={{google books |plainurl=y |id=v4R0GSJtEQ4C|page=1}}}}{{Pranala mati|date=Februari 2023 |bot=InternetArchiveBot |fix-attempted=yes }}, chapter 1</ref> Logaritma dilambangkan sebagai {{math|<sup>''b''</sup>log ''x''}} (dibaca "logaritma {{mvar|x}} dengan bilangan pokok {{mvar|b}}"). Terdapat definisi yang mirip dan lebih ringkas mengatakan bahwa fungsi {{math|<sup>''b''</sup>log}} [[Fungsi invers|invers]] dengan fungsi {{math|1=''x'' ↦ ''b''<sup>''x''</sup>}}. |
|||
Sebagai contoh, {{math|1=<sup>2</sup>log 16 = 4}}, karena {{math|1=2<sup>4</sup> = 2 × 2 × 2 × 2 = 16}}. Logaritma juga dapat bernilai negatif, contohnya {{math|1=<sup>2</sup>log {{sfrac|1=1|2=2}} = –1}}, karena {{math|1=2<sup>–1</sup> = {{sfrac|1=1|2=2<sup>1</sup>}} = {{sfrac|1=1|2=2}}}}. Logaritma juga berupa nilai desimal, sebagai contoh {{math|<sup>10</sup>log 150}} kira-kira sama dengan 2,176 karena terletak di antara 2 dan 3, dan begitupula 150 terletak antara {{math|1=10<sup>2</sup> = 100}} dan {{math|1=10<sup>3</sup> = 1000}}. Adapun sifat logaritma bahwa untuk setiap {{mvar|b}}, {{math|1=<sup>''b''</sup>log ''b'' = 1}} karena {{math|1=''b''<sup>1</sup> = {{mvar|b}}}}, dan {{math|1=<sup>''b''</sup>log 1 = 0}} karena {{math|1=''b''<sup>0</sup> = 1}}. |
|||
* [[Skala Richter]] mengukur intensitas [[gempa bumi]] dengan menggunakan skala logaritma berbasis 10. |
|||
== Identitas logaritma == |
|||
* Dalam astronomi, [[magnitudo]] yang mengukur terangnya bintang menggunakan skala logaritmik, karena [[mata]] manusia mempersepsikan terang secara logaritmik. |
|||
{{Main|Daftar identitas logaritma}} |
|||
Ada beberapa rumus penting yang mengaitkan logaritma dengan yang lainnya.<ref>Semua pernyataan di bagian ini dapat ditemukan pada {{Harvard citations|last1=Shirali|first1=Shailesh|year=2002|loc=bagian 4|nb=yes}}. Sebagai contoh, {{Harvard citations|last1=Downing|first1=Douglas|year=2003|loc=hlm. 275}}, atau {{Harvard citations|last1=Kate|last2=Bhapkar|year=2009|loc=hlm. 1-1|nb=yes}}.</ref> |
|||
=== Hasil kali, hasil bagi, pangkat, dan akar === |
|||
=== Penghitungan yang lebih mudah === |
|||
Logaritma dari hasil kali merupakan jumlah logaritma dari bilangan yang dikalikan, dan logaritma dari hasil bagi dari dua bilangan merupakan selisih logaritma. Logaritma dari bilangan pangkat ke-{{Mvar|p}} sama dengan ''{{Mvar|p}}'' dikali logaritma dari bilangan tersendiri, dan logaritma bilangan akar ke-{{Mvar|p}} sama dengan logaritma dibagi dengan {{Mvar|p}}. Tabel berikut memuat daftar sifat-sifat logaritma tersebut beserta contohnya. Masing-masing identitas ini diperoleh dari hasil substitusi dari definisi logaritma <math>x = b^{\, ^b\!\log x}</math> atau <math>y = b^{\, ^b\!\log y}</math> pada ruas kiri persamaan. |
|||
{| class="wikitable" style="margin: 0 auto;" |
|||
! |
|||
!Rumus |
|||
!Contoh |
|||
|- |
|||
|Hasil kali |
|||
|<math display="inline">^b\!\log(x y) = \, ^b\!\log x + \, ^b\!\log y</math> |
|||
|<math display="inline">^3\!\log 243 = \, ^3\!\log (9 \cdot 27) = ^3\!\log 9 + \, ^3\!\log 27 = 2 + 3 = 5</math> |
|||
|- |
|||
|Hasil bagi |
|||
|<math display="inline">^b\!\log \!\frac{x}{y} = \, ^b\!\log x - \, ^b\!\log y</math> |
|||
|<math display="inline">^2\!\log 16 = \, ^2\!\log \!\frac{64}{4} = \, ^2\!\log 64 - \, ^2\!\log 4 = 6 - 2 = 4</math> |
|||
|- |
|||
|Pangkat |
|||
|<math display="inline">^b\!\log\left(x^p\right) = p \, ^b\!\log x</math> |
|||
|<math display="inline">^2\!\log 64 = \, ^2\!\log \left(2^6\right) = 6 \cdot \, ^2\!\log 2 = 6</math> |
|||
|- |
|||
|Akar |
|||
|<math display="inline">^b\!\log \sqrt[p]{x} = \frac{^b\!\log x}{p}</math> |
|||
|<math display="inline">^{10}\!\log \sqrt{1000} = \, \frac{1}{2}\cdot \, ^{10}\!\log 1000 = \frac{3}{2} = 1,5</math> |
|||
|} |
|||
=== Mengubah bilangan pokok ===<!-- This section is linked from [[Mathematica]] --> |
|||
Logaritma {{math|<sup>''b''</sup>log ''x''}} dapat dihitung sebagai hasil bagi logaritma {{mvar|x}} dengan logaritma {{mvar|b}} terhadap bilangan pokok sembarang {{Mvar|k}}. Secara matematis dirumuskan sebagai: |
|||
: <math> ^b\!\log x = \frac{^k\!\log x}{^k\!\log b}.\, </math> |
|||
{{Collapse top|title=Bukti konversi antara logaritma dari bilangan pokok sembarang|width=80%}} |
|||
Dimulai dari identitas berikut |
|||
: <math> x = b^{^b\!\log x}, </math> |
|||
ini dapat menerapkan {{math|<sup>''k''</sup>log}} pada kedua ruas sehingga memperoleh |
|||
: <math> ^k\!\log x = \, ^k\!\log \left(b^{^b\!\log x}\right) = \, ^b\!\log x \cdot \, ^k\!\log b</math>. |
|||
Ketika mencari penyelesaian untuk {{math|1=<sup>''b''</sup>log ''x''}}, maka menghasilkan persamaan: |
|||
: <math> ^b\!\log x = \frac{^k\!\log x}{^k\!\log b}</math>. |
|||
Hal ini memperlihatkan faktor konversi dari nilai {{math|1=<sup>''k''</sup>log}} ke nilai {{math|1=<sup>''b''</sup>log}} yang serupa agar memperoleh bentuk {{math|1={{sfrac|1=1|2=<sup>''k''</sup>log ''b''}}}} |
|||
{{Collapse bottom}}[[Kalkulator ilmiah]] merupakan alat yang menghitung logaritma dengan bilangan pokok 10 dan {{mvar|[[e (konstanta matematika)|e]]}}.<ref>{{Citation|last1=Bernstein|first1=Stephen|last2=Bernstein|first2=Ruth|title=Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability|publisher=[[McGraw-Hill]]|location=New York|series=Schaum's outline series|isbn=978-0-07-005023-5|year=1999|url=https://archive.org/details/schaumsoutlineof00bern}}, hlm. 21</ref> Logaritma terhadap setiap bilangan pokok {{mvar|b}} dapat ditentukan menggunakan kedua logaritma tersebut melalui rumus sebelumnya: |
|||
: <math> ^b\!\log x = \frac{^{10}\!\log x}{^{10}\!\log b} = \frac{^{e}\!\log x}{^{e}\!\log b}.</math> |
|||
Diberikan suatu bilangan {{mvar|x}} dan logaritma {{math|1=''y'' = <sup>''b''</sup>log ''x''}}, dengan {{mvar|b}} adalah bilangan pokok yang tidak diketahui. Bilangan pokok tersebut dapat dinyatakan dengan |
|||
: <math> b = x^\frac{1}{y},</math> |
|||
Rumus ini dapat diperlihatkan dengan mengambil persamaan yang mendefinisikan {{math|1=''x'' = ''b''<sup><sup>''b''</sup>log ''x''</sup> = ''b''<sup>''y''</sup>}}, lalu dipangkatkan dengan {{math|1={{sfrac|1=1|2=y}}}}. |
|||
== Bilangan pokok khusus == |
|||
[[Berkas:Log4.svg|jmpl|Grafik logaritma dengan bilangan pokok 0,5; 2; dan {{mvar|e}}]] |
|||
Secara khusus, terdapat tiga bilangan pokok yang umum di antara semua pilihan bilangan pokok pada logaritma. Ketiga bilangan pokok tersebut adalah {{math|1=''b'' = 10}}, {{math|1=''b'' = [[e (konstanta matematika)|''e'']]}} (konstanta [[bilangan irasional]] yang kira-kira sama dengan 2,71828), dan {{math|1=''b'' = 2}} ([[logaritma biner]]). Dalam [[analisis matematika]], logaritma dengan bilangan pokok {{mvar|e}} tersebar karena sifat analitik yang dijelaskan di bawah. Di sisi lain, logaritma dengan {{nowrap|bilangan pokok 10}} mudah dipakai dalam perhitungan [[Transmisi manual|manual]] dalam sistem bilangan [[desimal]]:<ref>{{Citation|last1=Downing|first1=Douglas|title=Algebra the Easy Way|series=Barron's Educational Series|location=Hauppauge, NY|publisher=Barron's|isbn=978-0-7641-1972-9|date=2003|url=https://archive.org/details/algebraeasyway00down_0}}, chapter 17, hlm. 275</ref> |
|||
: <math>^{10}\!\log(10 x) = \, ^{10}\!\log 10 + \, ^{10}\!\log x = 1 + \, ^{10}\!\log x.\ </math> |
|||
Jadi, {{math|<sup>10</sup>log ''x''}} berkaitan dengan jumlah [[Digit|digit desimal]] dari bilangan bulat positif {{mvar|x}}: jumlah digitnya merupakan [[bilangan bulat]] terkecil yang lebih besar dari {{math|<sup>10</sup>log ''x''}}.<ref>{{Citation|last1=Wegener|first1=Ingo|title=Complexity theory: exploring the limits of efficient algorithms|publisher=[[Springer-Verlag]]|location=Berlin, New York|isbn=978-3-540-21045-0|date=2005}}, hlm. 20</ref> Sebagai contoh, {{math|<sup>10</sup>log 1430}} kira-kira sama dengan 3,15. Bilangan berikutnya merupakan jumlah digit dari 1430, yaitu 4. Dalam [[teori informasi]], logaritma alami dipakai dalam [[Nat (unit)|nat]] dan logaritma dengan bilangan pokok 2 dipakai dalam [[bit]] sebagai satuan dasar informasi.<ref>{{citation|title=Information Theory|first=Jan C. A.|last=Van der Lubbe|publisher=Cambridge University Press|date=1997|isbn=978-0-521-46760-5|page=3|url={{google books |plainurl=y |id=tBuI_6MQTcwC|page=3}}}}</ref> Logaritma biner juga dipakai dalam [[ilmu komputer]], dengan [[sistem biner]] ditemukan dimana-mana. Dalam [[teori musik]], rasio tinggi nada kedua (yaitu [[oktaf]]) ditemukan dimana-mana dan jumlah [[Sen (musik)|sen]] antara setiap dua tinggi nada dirumuskan sebagai konstanta 1200 dikali logaritma dari rasio (yaitu, 100 sen per [[setengah nada]] dengan [[temperamen sama]]). Dalam [[fotografi]], logaritma dengan bilangan pokok dua dipakai untuk mengukur [[nilai pajanan]], [[Luminans|tingkatan cahaya]], [[Kecepatan rana|waktu eksposur]], [[tingkap]], dan [[kecepatan film]] dalam "stop".<ref>{{citation|title=The Manual of Photography|first1=Elizabeth|last1=Allen|first2=Sophie|last2=Triantaphillidou|publisher=Taylor & Francis|date=2011|isbn=978-0-240-52037-7|page=228|url={{google books |plainurl=y |id=IfWivY3mIgAC|page=228}}}}</ref> |
|||
Tabel berikut memuat notasi-notasi umum mengenai bilangan pokok beserta bidang yang dipakai. Selain {{math|<sup>''b''</sup>log ''x''}}, adapula notasi logaritma lain yang ditulis sebagai {{math|log<sub>''b''</sub> ''x''}}, dan juga seperti {{math|log ''x''}}. Pada kolom "Notasi ISO" memuat penamaan yang disarankan [[Organisasi Standardisasi Internasional]], yakni [[ISO 80000-2]].<ref>Quantities and units–Part 2: Mathematics (ISO 80000-2:2019); EN ISO 80000-2</ref> Karena notasi {{math|log {{mvar|x}}}} telah dipakai untuk ketiga bilangan pokok di atas (atau ketika bilangan pokok belum ditentukan), bilangan pokok yang dimaksud harus sering diduga tergantung konteks atau bidangnya. Sebagai contoh, {{Math|log}} biasanya mengacu pada {{math|<sup>2</sup>log}} dalam ilmu komputer, dan {{Math|log}} mengacu pada {{math|<sup>''e''</sup>log}}.<ref>{{citation|first1=Michael T.|last1=Goodrich|author1-link=Michael T. Goodrich|first2=Roberto|last2=Tamassia|author2-link=Roberto Tamassia|title=Algorithm Design: Foundations, Analysis, and Internet Examples|publisher=John Wiley & Sons|date=2002|page=23}}{{quote|1=One of the interesting and sometimes even surprising aspects of the analysis of data structures and algorithms is the ubiquitous presence of logarithms ... As is the custom in the computing literature, we omit writing the base {{mvar|b}} of the logarithm when {{math|1=''b'' = 2}}.}}Terjemahan:{{quote|1=Salah satu hal yang menarik dan terkadang yang paling mengejutkan dalam aspek dari analisis struktur data beserta algoritma adalah bahwa keberadaan logaritma ada dimana-mana ... Menjadi kebiasaan dalam literatur komputer, kita menghilangkan penulisan bilangan pokok {{mvar|b}} dari logaritma ketika {{math|1=''b'' = 2}}.}}</ref> Dalam konteks lainnya, {{Math|log}} seringkali mengacu pada {{math|<sup>10</sup>log}}.<ref>{{citation|title=Introduction to Applied Mathematics for Environmental Science|edition=illustrated|first1=David F.|last1=Parkhurst|publisher=Springer Science & Business Media|date=2007|isbn=978-0-387-34228-3|page=288|url={{google books |plainurl=y |id=h6yq_lOr8Z4C|page=288 }}}}</ref> |
|||
Logaritma memindahkan fokus penghitungan dari bilangan normal ke pangkat-pangkat (eksponen). Bila basis logaritmanya sama, maka beberapa jenis penghitungan menjadi lebih mudah menggunakan logaritma:: |
|||
{| class="wikitable" style="text-align:center; margin:1em auto 1em auto;" |
|||
{| style="border:1px solid" align="center" |
|||
! scope="col" |Bilangan pokok |
|||
|- align="center" |
|||
{{mvar|b}} |
|||
! Penghitungan dengan angka !! Penghitungan dengan eksponen !! Identitas Logaritma |
|||
! scope="col" |Nama {{Math|<sup>''b''</sup>log ''x''}} |
|||
|- align="center" |
|||
! scope="col" |Notasi ISO |
|||
| <math> \!\, a b </math> || <math> \!\, A + B </math> || <math> \!\, \log(a b) = \log(a) + \log(b) </math> |
|||
! scope="col" |Notasi lain |
|||
|- align="center" |
|||
! scope="col" |Dipakai dalam bidang |
|||
| <math> \!\, a / b </math> || <math> \!\, A - B </math> || <math> \!\, \log(a / b) = \log(a) - \log(b) </math> |
|||
|- |
|||
|- align="center" |
|||
! scope="row" |2 |
|||
| <math> \!\, a ^ b </math> || <math> \!\, A b </math> || <math> \!\, \log(a ^ b) = b \log(a) </math> |
|||
|[[logaritma biner]] |
|||
|- align="center" |
|||
|{{math|lb ''x''}}<ref name="gullberg">{{Citation|title=Mathematics: from the birth of numbers.|author=Gullberg, Jan|location=New York|publisher=W. W. Norton & Co|date=1997|isbn=978-0-393-04002-9|url-access=registration|url=https://archive.org/details/mathematicsfromb1997gull}}</ref> |
|||
| <math> \!\, \sqrt[b]{a} </math> || <math> \!\, A / b </math> || <math> \!\, \log(\sqrt[b]{a}) = \frac{\log(a)}{b} </math> |
|||
|{{math|ld ''x''}}, {{math|log ''x''}}, {{math|lg ''x''}},<ref>See footnote 1 in {{citation|last1=Perl|first1=Yehoshua|last2=Reingold|first2=Edward M.|title=Understanding the complexity of interpolation search|journal=Information Processing Letters|date=December 1977|volume=6|issue=6|pages=219–22|doi=10.1016/0020-0190(77)90072-2}}</ref> {{math|<sup>2</sup>log ''x''}} |
|||
|[[ilmu komputer]], [[teori informasi]], [[bioinformatika]], [[teori musik]], [[fotografi]] |
|||
|- |
|||
! scope="row" |{{mvar|e}} |
|||
|[[logaritma alami]] |
|||
|{{math|ln ''x''}}{{refn|Beberapa para matematikawan menolak notasi ini. Dalam otobiografinya pada tahun 1985, [[Paul Halmos]] mengkritik bahwa "notasi ln bersifat kekanak-kanakan", karena menurutnya para matematikawan menggunakan notasi tersebut.<ref> |
|||
{{Citation |
|||
|title = I Want to Be a Mathematician: An Automathography |
|||
|author = Paul Halmos |
|||
|publisher = Springer-Verlag |
|||
|location=Berlin, New York |
|||
|date = 1985 |
|||
|isbn=978-0-387-96078-4 |
|||
}}</ref> |
|||
Notasi tersebut ditemukan oleh seorang matematikawan bernama [[Irving Stringham]].<ref> |
|||
{{Citation |
|||
|title = Uniplanar algebra: being part I of a propædeutic to the higher mathematical analysis |
|||
|author = Irving Stringham |
|||
|publisher = The Berkeley Press |
|||
|date = 1893 |
|||
|page = xiii |
|||
|url = {{google books |plainurl=y |id=hPEKAQAAIAAJ|page=13}} |
|||
}}</ref><ref> |
|||
{{Citation|title = Introduction to Financial Technology|author = Roy S. Freedman|publisher = Academic Press|location=Amsterdam|date = 2006|isbn=978-0-12-370478-8|page = 59|url = {{google books |plainurl=y |id=APJ7QeR_XPkC|page=5}}}}</ref>|name=adaa|group=nb}} |
|||
|{{math|log {{mvar|x}}}} (dipakai dalam matematika<ref>Lihat Teorema 3.29 di {{citation|last1=Rudin|first1=Walter|title=Principles of mathematical analysis|date=1984|publisher=McGraw-Hill International|location=Auckland|isbn=978-0-07-085613-4|edition=3rd ed., International student|url=https://archive.org/details/principlesofmath00rudi}}</ref> dan beberapa [[bahasa pemrograman]] lainnya{{refn|Contohnya seperti [[C (bahasa pemrograman)|C]], [[Java (bahasa pemrograman)|Java]], [[Haskell (bahasa pemrograman)|Haskell]], and [[Bahasa pemrograman BASIC|BASIC]].|group=nb}}), {{math|<sup>''e''</sup>log ''x''}} |
|||
|matematika, fisika, kimia, |
|||
[[statistik]], [[ekonomi]], teori informasi, dan rekayasa |
|||
|- |
|||
! scope="row" |10 |
|||
|[[logaritma biasa]] |
|||
|{{math|lg ''x''}} |
|||
|{{math|log ''x''}}, {{math|<sup>10</sup>log ''x''}} |
|||
(dipakai dalam rekayasa, biologi, dan astronomi) |
|||
|bidang berbagai [[rekayasa]] (lihat [[Decibel|desibel]] dan lihat di bawah), |
|||
[[tabel]] logaritma, [[kalkulator]] genggam, [[spektroskopi]] |
|||
|- |
|||
! scope="row" |{{mvar|b}} |
|||
|logaritma dengan bilangan pokok {{mvar|b}} |
|||
|{{math|<sup>''b''</sup>log ''x''}} |
|||
| |
|||
|matematika |
|||
|} |
|} |
||
== Sejarah == |
|||
Sifat-sifat diatas membuat penghitungan dengan eksponen menjadi lebih mudah, dan penggunaan logaritma sangat penting, terutama sebelum tersedianya [[kalkulator]] sebagai hasil perkembangan teknologi modern. |
|||
{{Main|Sejarah logaritma}} |
|||
'''Sejarah logaritma''' yang dimulai dari Eropa pada abad ketujuh belas merupakan penemuan [[Fungsi (matematika)|fungsi]] terbaru yang memperluas dunia analisis di luar keterbatasan metode aljabar. Metode logaritma dikemukakan secara terbuka oleh [[John Napier]] pada tahun 1614, dalam bukunya yang berjudul ''[[Mirifici Logarithmorum Canonis Descriptio]]''.<ref>{{citation|first=John|last=Napier|author-link=John Napier|title=Mirifici Logarithmorum Canonis Descriptio|trans-title=The Description of the Wonderful Rule of Logarithms|language=la|location=Edinburgh, Scotland|publisher=Andrew Hart|year=1614|url=http://gdz.sub.uni-goettingen.de/dms/load/img/?PPN=PPN527914568&DMDID=DMDLOG_0001&LOGID=LOG_0001&PHYSID=PHYS_0001}}</ref><ref>{{Citation|first=Ernest William|last=Hobson|title=John Napier and the invention of logarithms, 1614|year=1914|publisher=The University Press|location=Cambridge|url=https://archive.org/details/johnnapierinvent00hobsiala}}</ref> Namun, teknik-teknik lain sebelum penemuan Napier sudah ada dengan keterbatasan metode yang serupa, contohnya seperti [[prosthafaeresis]] atau penggunaan tabel barisan, yang dikembangkan dengan luas oleh [[Jost Bürgi]] sekitar tahun 1600.<ref name="folkerts">{{citation|last1=Folkerts|first1=Menso|last2=Launert|first2=Dieter|last3=Thom|first3=Andreas|arxiv=1510.03180|doi=10.1016/j.hm.2016.03.001|issue=2|journal=[[Historia Mathematica]]|mr=3489006|pages=133–147|title=Jost Bürgi's method for calculating sines|volume=43|year=2016|s2cid=119326088}}</ref><ref>{{MacTutor|id=Burgi|title=Jost Bürgi (1552–1632)}}</ref> Napier menciptakan istilah untuk logaritma dalam [[bahasa Latin]] Tengah, “logaritmus”, yang berasal dari gabungan dua kata Yunani, ''logos'' “proporsi, rasio, kata” + ''arithmos'' “bilangan”. Secara harfiah, "logaritmus" berarti “bilangan rasio”. |
|||
[[Logaritma umum]] dari bilangan adalah indeks dari perpangkatan sepuluh yang sama dengan bilangan tersebut.<ref>William Gardner (1742) ''Tables of Logarithms''</ref> Bilangan yang sangat membutuhkan banyak angka merupakan kiasan kasar untuk logaritma umum, dan [[Archimedes]] menyebutnya sebagai “orde bilangan”.<ref>{{citation|last=Pierce|first=R. C. Jr.|date=January 1977|doi=10.2307/3026878|issue=1|journal=[[The Two-Year College Mathematics Journal]]|jstor=3026878|pages=22–26|title=A brief history of logarithms|volume=8}}</ref> Logaritma real pertama adalah metode heuristik yang mengubah perkalian menjadi penjumlahan, sehingga memudahkan perhitungan yang cepat. Ada beberapa metode yang menggunakan tabel yang diperoleh dari identitas trigonometri,<ref>Enrique Gonzales-Velasco (2011) ''Journey through Mathematics–Creative Episodes in its History'', §2.4 Hyperbolic logarithms, hlm. 117, Springer {{isbn|978-0-387-92153-2}}</ref> dan metode tersebut dinamakan [[prosthafaeresis]]. |
|||
Untuk mengkali dua angka, yang diperlukan adalah melihat logaritma masing-masing angka dalam tabel, menjumlahkannya, dan melihat antilog jumlah tersebut dalam tabel. Untuk mengitung pangkat atau akar dari sebuah bilangan, logaritma bilangan tersebut dapat dilihat di tabel, lalu hanya mengkali atau membagi dengan ''radix'' pangkat atau akar tersebut. |
|||
Penemuan [[Fungsi (matematika)|fungsi]] yang dikenal saat ini sebagai [[logaritma alami]], berawal dari saat [[Grégoire de Saint-Vincent]] mencoba menggambarkan [[Kuadratur (matematika)|kuadratur]] [[hiperbola]] persegi panjang. Archimedes menulis risalah yang berjudul ''[[Quadrature of the Parabola|The Quadrature of the Parabola]]'' pada abad ke-3 SM, tetapi kuadratur hiperbola menghindari semua upayanya hingga Saint-Vincent menerbitkan hasilnya pada tahun 1647. Logaritma yang mengaitkan [[barisan dan deret geometri]] dalam [[Argumen dari fungsi|argumen]] dan nilai [[barisan dan deret aritmetika]], meminta [[A. A. de Sarasa|Antonio de Sarasa]] untuk mengaitkan kuadratur Saint-Vincent dan tradisi logaritma dalam [[prosthafaeresis]] sehingga mengarah ke sebuah persamaan kata untuk logaritma alami, yaitu "logaritma hiperbolik". [[Christiaan Huygens]] dan [[James Gregory (matematikawan)|James Gregory]] mulai mengenali fungsi baru tersebut. [[Gottfried Wilhelm Leibniz|Leibniz]] memakai notasi Log y pada tahun 1675,<ref>[[Florian Cajori]] (1913) "History of the exponential and logarithm concepts", [[American Mathematical Monthly]] 20: 5, 35, 75, 107, 148, 173, 205.</ref> dan tahun berikutnya ia mengaitkannya dengan [[Kalkulus integral|integral]] |
|||
=== Kalkulus === |
|||
[[Turunan]] fungsi logaritma adalah |
|||
: <math>\frac{d}{dx} \log_b(x) = \frac{1}{x \ln(b)} = \frac{\log_b(e)}{x}</math> |
|||
dimana ln adalah logaritma natural, yaitu logaritma yang berbasis ''e''. Jika ''b'' = ''e'', maka rumus diatas dapat disederhanakan menjadi |
|||
: <math>\frac{d}{dx} \ln(x) = \frac{1}{x}.</math> |
|||
: <math>\int \frac{dy}{y}.</math> |
|||
[[Integral]] fungsi logaritma adalah |
|||
: <math>\int \log_b(x) \,dx = x \log_b(x) - \frac{x}{\ln(b)} + C = x \log_b \left(\frac{x}{e}\right) + C.</math> |
|||
Sebelum Euler mengembangkan konsep modernnya tentang logaritma alami kompleks, [[Roger Cotes#Matematika|Roger Cotes]] memperlihatkan hasil yang hampir sama pada tahun 1714 bahwa<ref>{{citation|last1=Stillwell|first1=J.|title=Mathematics and Its History|date=2010|publisher=Springer|edition=3}}</ref> |
|||
== Penghitungan nilai logaritma == |
|||
Nilai logaritma dengan basis b dapat dihitung dengan rumus dibawah ini. |
|||
: <math> |
: <math>\log(\cos \theta + i\sin \theta) = i\theta</math>. |
||
== Tabel logaritma, mistar hitung, dan penerapan bersejarah == |
|||
Sedangkan untuk logaritma berbasis e dan berbasis 2, terdapat prosedur-prosedur yang umum. (Lihat juga artikel [[logaritma natural]] dan [[logaritma biner]]. |
|||
[[Berkas:Logarithms Britannica 1797.png|ka|jmpl|360x360px|Penjelasan logaritma dalam ''[[Encyclopædia Britannica]]'' pada tahun 1797.]] |
|||
Dengan menyederhanakan perhitungan yang rumit sebelum adanya mesin hitung komputer, logaritma berkontribusi pada kemajuan pengetahuan, khususnya [[astronomi]]. Logaritma sangat penting terhadap kemajuan dalam [[Ilmu ukur wilayah|survei]], [[navigasi benda langit]], dan cabang lainnya. [[Pierre-Simon Laplace]] menyebut logaritma sebagai |
|||
:: "...kecerdasan yang mengagumkan, [sebuah alat] yang mengurangi pekerjaan berbulan-bulan menjadi beberapa hari, menggandakan kehidupan astronom, dan menghindarinya dari kesalahan dan rasa jijik yang tak terpisahkan dari perhitungan yang panjang."<ref>{{Citation|last1=Bryant|first1=Walter W.|title=A History of Astronomy|url=https://archive.org/stream/ahistoryastrono01bryagoog#page/n72/mode/2up|publisher=Methuen & Co|location=London|year=1907}}, hlm. 44<br>Teks asli:{{quote|1="...[a]n admirable artifice which, by reducing to a few days the labour of many months, doubles the life of the astronomer, and spares him the errors and disgust inseparable from long calculations."}}</ref> |
|||
{{anchor|Antilogaritma}}Karena fungsi {{math|''f''(''x'') {{=}} {{mvar|b}}<sup>''x''</sup>}} adalah fungsi invers dari {{math|<sup>''b''</sup>log ''x''}}, maka fungsi tersebut disebut sebagai '''antilogaritma'''.<ref>{{Citation|editor1-last=Abramowitz|editor1-first=Milton|editor1-link=Milton Abramowitz|editor2-last=Stegun|editor2-first=Irene A.|editor2-link=Irene Stegun|title=Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables|publisher=[[Dover Publications]]|location=New York|isbn=978-0-486-61272-0|edition=10th|year=1972|title-link=Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables}}, bagian 4.7., hlm. 89</ref> Saat ini, antilogaritma lebih sering disebut [[fungsi eksponensial]]. |
|||
[[Kategori:Matematika]] |
|||
=== Tabel logaritma === |
|||
[[bg:Логаритъм]] |
|||
Sebuah alat penting yang memungkinkan penggunaan logaritma adalah [[tabel logaritma]].<ref>{{Citation|last1=Campbell-Kelly|first1=Martin|title=The history of mathematical tables: from Sumer to spreadsheets|title-link=The History of Mathematical Tables|publisher=[[Oxford University Press]]|series=Oxford scholarship online|isbn=978-0-19-850841-0|year=2003}}, bagian 2</ref> Tabel logaritma pertama kali disusun oleh [[Henry Briggs (matematikawan)|Henry Briggs]] pada tahun 1617 setelah penemuan Napier, tetapi penemuannya menggunakan 10 sebagai bilangan pokok. Tabel pertamanya memuat [[logaritma umum]] dari semua bilangan bulat yang berkisar antara 1 dengan 1000, dengan ketepatan yang dimiliki 14 digit, dan kemudian ia membuat tabel dengan kisaran yang besar. Tabel tersebut mencantumkan nilai <math>^{10}\!\log x</math> untuk setiap bilangan <math>x</math> dalam kisaran dan ketepatan tertentu. Karena bilangan yang berbeda dengan faktor 10 memiliki logaritma yang berbeda dengan bilangan bulat, logaritma dengan bilangan pokok 10 digunakan secara universal untuk perhitungan, sehingga disebut logaritma umum. Logaritma umum dari <math>x</math> dipisahkan menjadi [[Fungsi bilangan bulat terbesar dan terkecil|bagian bilangan bulat]] yang dikenal sebagai karakteristik, dan [[bagian pecahan]] ({{Lang-en|fractional part}}) yang dikenal sebagai [[Logaritma umum#Mantissa dan karakteristiknya|mantissa]]. Tabel logaritma hanya perlu menyertakan mantissa, karena karakteristik logaritma umum dapat dengan mudah ditentukan dengan menghitung angka dari titik desimal.<ref>{{Citation|last1=Spiegel|first1=Murray R.|last2=Moyer|first2=R.E.|title=Schaum's outline of college algebra|publisher=[[McGraw-Hill]]|location=New York|series=Schaum's outline series|isbn=978-0-07-145227-4|year=2006}}, hlm. 264</ref> Karakteristik logaritma umum dari <math>10 \cdot x</math> sama dengan satu ditambah karakteristik <math>x</math>, dan mantissanya sama. Dengan menggunakan tabel logartima dengan tiga digit, nilai logaritma dari 3542 kira-kira sama dengan |
|||
[[ca:Logaritme]] |
|||
[[cs:Logaritmus]] |
|||
: <math>^{10}\!\log 3542 = \,^{10}\!\log (1000 \cdot 3,542) = 3 + \,^{10}\!\log 3,542 \approx 3 + \,^{10}\!\log 3,54</math> |
|||
[[da:Logaritme]] |
|||
[[de:Logarithmus]] |
|||
Nilainya dengan ketepatan yang sangat tinggi dapat diperoleh melalui [[interpolasi]]: |
|||
[[en:Logarithm]] |
|||
[[es:Logaritmo]] |
|||
: <math>^{10}\!\log 3542 \approx 3 + ^{10}\!\log 3,54 + 0,2 \cdot (\, ^{10}\!\log 3,55 - \,^{10}\!\log 3,54)</math> |
|||
[[eo:Logaritmo]] |
|||
[[fr:Logarithme]] |
|||
Nilai <math>10^x</math> dapat ditentukan dengan pencarian terbalik pada tabel yang sama, karena logaritma merupakan [[fungsi monoton]]. |
|||
[[gl:Función logaritmo]] |
|||
[[ko:로그]] |
|||
=== Perhitungan === |
|||
[[io:Logaritmo]] |
|||
Hasil kali atau hasil bagi dari dua bilangan positif {{Mvar|c}} dan ''{{Mvar|d}}'' biasanya dihitung sebagai penambahan dan pengurangan logaritma. Hasil kali {{Math|''cd''}} berasal dari antilogaritma dari penambahan dan hasil bagi {{Math|{{sfrac|1=''c''|2=''d''}}}} berasal dari antilogaritma dari pengurangan, melalui tabel yang sama: |
|||
[[it:Logaritmo]] |
|||
[[he:לוגריתם]] |
|||
: <math> cd = 10^{\, ^{10}\!\log c} \, 10^{\,^{10}\!\log d} = 10^{\,^{10}\!\log c \, + \, ^{10}\!\log d}</math> |
|||
[[la:Logarithmus]] |
|||
[[lv:Logaritms]] |
|||
dan |
|||
[[hu:Logaritmus]] |
|||
[[nl:Logaritme]] |
|||
: <math>\frac c d = c d^{-1} = 10^{\, ^{10}\!\log c \, - \, ^{10}\!\log d}.</math> |
|||
[[ja:対数]] |
|||
[[no:Logaritme]] |
|||
Untuk perhitungan manual yang meminta ketelitian yang cukup besar, melakukan pencarian kedua logaritma, menghitung jumlah atau selisihnya, dan mencari antilogaritma jauh lebih cepat daripada menghitung perkalian dengan metode sebelumnya seperti [[prosthafaeresis]], yang mengandalkan [[identitas trigonometri]]. |
|||
[[pl:Logarytm]] |
|||
[[pt:Logaritmo]] |
|||
Perhitungan pangkat direduksi menjadi perkalian, dan sedangkan perhitungan [[Akar ke-n|akar]] direduksi menjadi pembagian. Pernyataan ini dapat dilihat sebagai |
|||
[[ro:Logaritm]] |
|||
[[ru:Логарифм]] |
|||
: <math>c^d = \left(10^{\, ^{10}\!\log c}\right)^d = 10^{\, d \, ^{10}\!\log c}</math> |
|||
[[sk:Logaritmus]] |
|||
[[sl:Logaritem]] |
|||
dan |
|||
[[sr:Логаритам]] |
|||
[[fi:Logaritmi]] |
|||
: <math>\sqrt[d]{c} = c^\frac{1}{d} = 10^{\frac{1}{d} \, ^{10}\!\log c}.</math> |
|||
[[sv:Logaritm]] |
|||
[[tr:Logaritma]] |
|||
Perhitungan trigonometri dilengkapi dengan tabel-tabel yang memuat logaritma umum dari [[fungsi trigonometri]]. |
|||
[[zh:对数]] |
|||
=== Mistar hitung === |
|||
Penerapan penting lainnya adalah [[mistar hitung]], sepasang skala yang dibagi secara logaritmik yang digunakan dalam perhitungan. Adapun skala logaritmik yang tidak memiliki sorong, [[mistar Gunter]], ditemukan tak lama setelah penemuan Napier dan disempurnakan oleh [[William Oughtred]] untuk menciptakan sepasang skala logaritmik yang dapat dipindahkan terhadap satu sama lain, yaitu mistar hitung. Angka yang ditempatkan pada skala hitung pada jarak sebanding dengan selisih antara logaritmanya. Menggeser skala atas dengan tepat berarti menambahkan logaritma secara mekanis, seperti yang diilustrasikan berikut ini: |
|||
[[Berkas:Slide rule example2 with labels.svg|al=alt=A slide rule: two rectangles with logarithmically ticked axes, arrangement to add the distance from 1 to 2 to the distance from 1 to 3, indicating the product 6.|pus|jmpl|550x550px|Penggambaran skema mengenai mistar hitung. Dimulai dari 2 pada skala di bawah, lalu tambahkan dengan jarak ke 3 pada skala atas agar mencapai hasil kali 6. Mistar hitung bekerja karena ditandai sedemikian rupa sehingga jarak dari 1 ke {{math|1=''x''}} sebanding dengan logaritma {{math|1=''x''}}.]] |
|||
Sebagai contoh, dengan menambahkan jarak dari 1 ke 2 pada skala di bagian bawah ke jarak dari 1 ke 3 pada skala di bagian atas menghasilkan hasil kali 6, yang dibacakan di bagian bawah. Mistar hitung adalah sebuah alat menghitung yang penting bagi para insinyur dan ilmuwan hingga tahun 1970-an, karena dengan mengorbankan ketepatan nilai memungkinkan perhitungan yang jauh lebih cepat daripada teknik berdasarkan tabel.<ref name="ReferenceA2">{{Citation|last1=Maor|first1=Eli|title=E: The Story of a Number|publisher=[[Princeton University Press]]|isbn=978-0-691-14134-3|year=2009|at=bagian 1, 13}}</ref> |
|||
== Sifat analitik == |
|||
Kajian yang lebih dalam mengenai logaritma memerlukan sebuah konsep yang disebut ''[[Fungsi (matematika)|fungsi]]''. Fungsi merupakan sebuah kaidah yang dipetakan suatu bilangan akan menghasilkan bilangan lain.<ref>{{citation|last1=Devlin|first1=Keith|author1-link=Keith Devlin|title=Sets, functions, and logic: an introduction to abstract mathematics|publisher=Chapman & Hall/CRC|location=Boca Raton, Fla|edition=3rd|series=Chapman & Hall/CRC mathematics|isbn=978-1-58488-449-1|year=2004|url={{google books |plainurl=y |id=uQHF7bcm4k4C}}}}, atau lihat referensinya di [[Fungsi (matematika)#Referensi|fungsi]].</ref> Contohnya seperti fungsi yang menghasilkan bilangan konstan {{mvar|b}}, yang dipangkatkan setiap bilangan real {{mvar|x}}. Fungsi ini secara matematis ditulis sebagai {{math|1=''f''(''x'') = {{mvar|b}}<sup> ''x''</sup>}}. Ketika {{mvar|b}} positif dan tak sama dengan 1, maka {{Mvar|f}} adalah fungsi terbalikkan ketika dianggap sebagai fungsi dengan interval dari bilangan real ke bilangan real positif. |
|||
=== Keberadaan === |
|||
Misalkan {{mvar|b}} adalah bilangan real positif yang tidak sama dengan 1 dan misalkan {{math|1=''f''(''x'') = {{mvar|b}}<sup> ''x''</sup>}}. Pernyataan yang diikuti dari [[teorema nilai antara]] ini,<ref name="LangIII.3">{{Citation|last1=Lang|first1=Serge|title=Undergraduate analysis|year=1997|series=[[Undergraduate Texts in Mathematics]]|edition=2nd|location=Berlin, New York|publisher=[[Springer-Verlag]]|doi=10.1007/978-1-4757-2698-5|isbn=978-0-387-94841-6|mr=1476913|author1-link=Serge Lang}}, bagian III.3</ref> merupakan hasil standar dalam analisis real yang mengatakan bahwa setiap fungsi monoton sempurna dan kontinu merupakan fungsi bijektif antara ranah ({{Lang-en|domain}}) dan kisarannya ({{Lang-en|range}}). Pernyataan saat ini mengatakan bahwa {{mvar|f}} yang [[Fungsi monoton|menaik sempurna]] (untuk {{math|''b'' > 1}}), atau menurun sempurna (untuk {{math|0 < {{mvar|b}} < 1}})<ref name="LangIV.2">{{Harvard citations|last1=Lang|year=1997|nb=yes|loc=bagian IV.2}}</ref> merupakan [[fungsi kontinu]], memiliki ranah <math>\R</math> dan memiliki kisaran <math>\R_{> 0}</math>. Oleh karena itu, {{Mvar|f}} adalah fungsi bijeksi dari <math>\R</math> ke <math>\R_{>0}</math>. Dengan kata lain, untuk setiap bilangan real positif {{Mvar|y}}, terdapat setidaknya satu bilangan real {{Mvar|x}} sehingga <math>b^x = y</math>. |
|||
Misalkan <math>^b\!\log\colon\R_{>0}\to\R</math> yang menyatakan invers dari fungsi {{Mvar|f}}. Dalam artian, {{math|<sup>''b''</sup>log ''y''}} adalah bilangan real tunggal {{mvar|x}} sehingga <math>b^x = y</math>. Fungsi ini disebut ''fungsi logaritma'' dengan bilangan pokok-{{Mvar|b}} atau ''fungsi logaritmik'' (atau ''logaritma'' saja). |
|||
=== Karakterisasi melalui rumus hasil kali === |
|||
Pada dasarnya, fungsi {{math|<sup>''b''</sup>log ''x''}} juga dapat dikarakterisasikan melalui rumus hasil kali |
|||
: <math>^b\!\log(xy) = \, ^b\!\log x + \, ^b\!\log y.</math> |
|||
Lebih tepatnya, logaritma untuk setiap bilangan pokok {{math|''b'' > 1}} yang hanya merupakan [[Fungsi menaik|fungsi {{Math|''f''}} naik]] dari bilangan real positif ke bilangan real memenuhi sifat bahwa {{math|1=''f''(''b'') = 1}} dan<ref>{{citation|title=Foundations of Modern Analysis|volume=1|last=Dieudonné|first=Jean|page=84|year=1969|publisher=Academic Press}} item (4.3.1)</ref> |
|||
: <math>f(xy)=f(x)+f(y).</math> |
|||
=== Grafik fungsi logaritma === |
|||
[[Berkas:Logarithm inversefunctiontoexp.svg|al=The graphs of two functions.|ka|jmpl|Grafik fungsi logaritma {{math|<sup>''b''</sup>log (''x'')}} (berwarna biru) diperoleh dengan [[Refleksi (matematika)|mencerminkan]] grafik fungsi {{math|''b''<sup>''x''</sup>}} (berwarna merah) di garis diagonal({{math|1=''x'' = {{mvar|y}}}}).]] |
|||
Seperti yang dibahas sebelumnya, fungsi {{math|<sup>''b''</sup>log}} invers terhadap fungsi eksponensial <math>x\mapsto b^x</math>. Karena itu, [[Grafik fungsi|grafiknya]] berkorespondensi dengan satu sama lain saat menukar koordinat-{{mvar|x}} dan koordinat-{{mvar|y}} (atau saat melakukan pencerminan di garis diagonal {{Math|1=''x'' = ''y''}}), seperti yang diperlihatkan sebagai berikut: sebuah titik {{math|1=(''t'', ''u'' = {{mvar|b}}<sup>''t''</sup>)}} pada grafik dari {{Mvar|f}} menghasilkan sebuah titik {{math|1=(''u'', ''t'' = <sup>''b''</sup>log ''u'')}} pada grafik logaritma dan sebaliknya. Akibatnya, {{math|<sup>''b''</sup>log (''x'')}} [[Limit barisan|divergen menuju takhingga]] (dalam artian semakin besar dari setiap bilangan yang diberikan) jika {{mvar|x}} naik menuju takhingga, asalkan {{mvar|b}} lebih besar dari satu. Pada kasus tersebut, {{math|<sup>''b''</sup>log(''x'')}} merupakan [[fungsi menaik]]. Sedangkan untuk kasus {{math|''b'' < 1}}, {{math|<sup>''b''</sup>log (''x'')}} cenderung menuju ke negatif takhingga. Ketika {{mvar|x}} mendekati nol, {{math|<sup>''b''</sup>log ''x''}} menuju ke negatif takhingga untuk {{math|''b'' > 1}} dan menuju ke plus takhingga untuk {{math|''b'' < 1}}. |
|||
=== Turunan dan antiturunan === |
|||
[[Berkas:Logarithm derivative.svg|al=Sebuah grafik fungsi logaritma dan sebuah garis yang menyinggungnya di sebuah titik.|ka|jmpl|220x220px|Grafik fungsi [[logaritma alami]] (berwarna hijau) beserta garis singgungnya di {{math|''x'' {{=}} 1,5}} (berwarna hitam)]] |
|||
Sifat analitik tentang fungsi adalah melalui fungsi inversnya.<ref name="LangIII.3" /> Jadi, ketika {{math|1=''f''(''x'') = {{mvar|b}}<sup>''x''</sup>}} adalah fungsi kontinu dan [[Fungsi terdiferensialkan|terdiferensialkan]], maka {{math|<sup>''b''</sup>log ''y''}} fungsi kontinu dan terdiferensialkan juga. Penjelasan kasarnya, sebuah fungsi kontinu adalah terdiferensialkan jika grafiknya tidak mempunyai "ujung" yang tajam. Lebih lanjut, ketika [[turunan]] dari {{math|''f''(''x'')}} menghitung nilai {{math|ln(''b'') ''b''<sup>''x''</sup>}} melalui sifat-sifat [[fungsi eksponensial]], [[aturan rantai]] menyiratkan bahwa turunan dari {{math|<sup>''b''</sup>log ''x''}} dirumuskan sebagai <ref name="LangIV.2" /><ref>{{citation|work=Wolfram Alpha|title=Calculation of ''d/dx(Log(b,x))''|publisher=[[Wolfram Research]]|access-date=15 Maret 2011|url=http://www.wolframalpha.com/input/?i=d/dx(Log(b,x))}}</ref> |
|||
: <math>\frac{d}{dx} \, ^b\!\log x = \frac{1}{x\ln b}. </math> |
|||
Artinya, [[kemiringan]] dari [[garis singgung]] yang menyinggung grafik logaritma dengan bilangan pokok {{math|''b''}} di titik {{math|(''x'', <sup>''b''</sup>log (''x''))}} sama dengan {{math|{{sfrac|1=1|2=''x'' ln(''b'')}}}}. |
|||
Turunan dari {{Math|ln(''x'')}} adalah {{Math|{{sfrac|1=1|2=''x''}}}}, yang berarti ini menyiratkan bahwa {{Math|ln(''x'')}} adalah [[integral]] tunggal dari {{math|{{sfrac|1=1|2=''x''}}}} yang mempunyai nilai 0 untuk {{math|1=''x'' = 1}}. Hal ini merupakan rumus paling sederhana yang mendorong sifat "alami" pada logaritma alami, dan hal ini juga merupakan salah satu alasan pentingnya konstanta [[E (konstanta matematika)|{{Mvar|e}}]]. |
|||
Turunan dengan argumen fungsional rampat {{math|''f''(''x'')}} dirumuskan sebagai |
|||
: <math>\frac{d}{dx} \ln f(x) = \frac{f'(x)}{f(x)}.</math> |
|||
Hasil bagi pada ruas kanan disebut [[turunan logaritmik]] dari ''{{Mvar|f}}'' dan menghitung {{math|''f<nowiki>'</nowiki>''(''x'')}} melalui turunan dari {{math|ln(''f''(''x''))}} dikenal sebagai [[pendiferensialan logaritmik]].<ref>{{Citation|last1=Kline|first1=Morris|author1-link=Morris Kline|title=Calculus: an intuitive and physical approach|publisher=[[Dover Publications]]|location=New York|series=Dover books on mathematics|isbn=978-0-486-40453-0|year=1998}}, hlm. 386</ref> Antiturunan dari [[logaritma alami]] {{math|ln(''x'')}} dirumuskan sebagai:<ref>{{citation|work=Wolfram Alpha|title=Calculation of ''Integrate(ln(x))''|publisher=Wolfram Research|access-date=15 Maret 2011|url=http://www.wolframalpha.com/input/?i=Integrate(ln(x))}}</ref> |
|||
: <math>\int \ln(x) \,dx = x \ln(x) - x + C.</math> |
|||
Terdapat [[Daftar integral dari fungsi logaritmik|rumus yang berkaitan]], seperti antiturunan dari logaritma dengan bilangan pokok lainnya dapat diperoleh dari persamaan ini dengan mengubah bilangan pokoknya.<ref>{{Harvard citations|editor1-last=Abramowitz|editor2-last=Stegun|year=1972|nb=yes|loc=hlm. 69}}</ref> |
|||
=== Representasi integral mengenai fungsi logaritma === |
|||
[[Berkas:Natural logarithm integral.svg|al=A hyperbola with part of the area underneath shaded in grey.|jmpl|[[Logaritma alami|Logaritma natural]] dari ''{{Mvar|t}}'' adalah luas yang diwarnai di bawah grafik fungsi {{math|1=''f''(''x'') = {{sfrac|1=1|2=''x''}}}}.]] |
|||
[[Logaritma alami]] dari {{Mvar|t}} dapat didefinisikan sebagai [[integral tentu]]: |
|||
: <math>\ln t = \int_1^t \frac{1}{x} \, dx.</math> |
|||
Definisi ini menguntungkan karena tidak bergantung pada fungsi eksponensial atau fungsi trigonometri apapun, dan definisi ini merupakan sebuah integral dari fungsi timbal balik sederhana. Penjelasan dalam integral, {{math|ln(''t'')}} sama dengan luas antara sumbu-{{mvar|x}} dan grafik fungsi {{math|{{sfrac|1=1|2=''x''}}}}, yang berkisar dari {{math|1=''x'' = 1}} ke {{math|1=''x'' = ''t''}}. Penjelasan ini juga merupakan akibat dari [[teorema dasar kalkulus]], dan bahkan turunan dari {{math|ln(''x'')}} sama dengan {{math|{{sfrac|1=1|2=''x''}}}}. Rumus logaritma hasil kali dan pangkat dapat diperoleh melalui definisi ini.<ref>{{Citation|last1=Courant|first1=Richard|title=Differential and integral calculus. Vol. I|publisher=[[John Wiley & Sons]]|location=New York|series=Wiley Classics Library|isbn=978-0-471-60842-4|mr=1009558|year=1988}}, bagian III.6</ref> Sebagai contoh, rumus hasil kali {{math|1=ln(''tu'') = ln(''t'') + ln(''u'')}} dapat disimpulkan sebagai: |
|||
: <math> \ln(tu) = \int_1^{tu} \frac{1}{x} \, dx \ \stackrel {(1)} = \int_1^{t} \frac{1}{x} \, dx + \int_t^{tu} \frac{1}{x} \, dx \ \stackrel {(2)} = \ln(t) + \int_1^u \frac{1}{w} \, dw = \ln(t) + \ln(u).</math> |
|||
Persamaan (1) membagi integral menjadi dua bagian, sementara (2) mengubah variabel {{Math|''w''}} menjadi {{Math|{{sfrac|1=''x''|2=''t''}}}}. Pada ilustrasi dibawah, pembagian integral tersebut dapat disamakan dengan pembagian luasnya menjadi bagian berwarna kuning dan biru. Dengan mengukur luas berwarna biru kembali secara vertikal melalui faktor {{Mvar|t}} dan menyusutnya melalui faktor yang sama secara horizontal tidak mengubah ukuran luasnya. Dengan memindahkan daerah biru ke daerah kuning, luasnya menyesuaikan grafik fungsi {{math|1=''f''(''x'') = {{sfrac|1=1|2=''x''}}}} lagi. Oleh karena itu, luas biru di sebelah kiri, yang merupakan integral dari fungsi {{math|''f''(''x'')}} dengan interval dari {{Mvar|t}} hingga {{Mvar|tu}} sama dengan integral dari fungsi yang sama dengan interval 1 hingga {{Mvar|u}}. Hal ini membenarkan persamaan (2) melalui bukti geometri lainnya. |
|||
[[Berkas:Natural logarithm product formula proven geometrically.svg|al=Fungsi hiperbola digambarkan dua kali. Luas di bawah fungsi dibagi menjadi bagian yang berbeda.|pus|jmpl|500x500px|Sebuah bukti visual tentang rumus hasil kali dari logaritma natural]] |
|||
Rumus pangkat {{math|1=ln(''t''<sup>''r''</sup>) = ''r'' ln(''t'')}} dapat real dalam cara yang serupa: |
|||
: <math> |
|||
\ln(t^r) = \int_1^{t^r} \frac{1}{x}dx = \int_1^t \frac{1}{w^r} \left(rw^{r - 1} \, dw\right) = r \int_1^t \frac{1}{w} \, dw = r \ln(t). |
|||
</math> |
|||
Persamaan kedua menggunakan perubahan variabel {{math|1=''w'' = {{mvar|x}}<sup>{{sfrac|1=1|2=''r''}}</sup>}} melalui [[integral substitusi]]. |
|||
Jumlah keseluruhan timbal balik dari bilangan asli yang dirumuskan |
|||
: <math>1 + \frac 1 2 + \frac 1 3 + \cdots + \frac 1 n = \sum_{k=1}^n \frac{1}{k},</math> |
|||
disebut [[Deret harmonik (matematika)|deret harmonik]]. Deret ini sangat terkait erat dengan [[logaritma alami]], yang dinyatakan melalui pernyataan berikut: ketika {{Mvar|n}} cenderung menuju [[Tak hingga|takhingga]], selisih dari |
|||
: <math>\sum_{k=1}^n \frac{1}{k} - \ln(n),</math> |
|||
[[Limit barisan|konvergen]] (yakni mendekati dengan sembarang) ke sebuah bilangan yang dikenal sebagai [[konstanta Euler–Mascheroni]] {{math|1=''γ'' = 0,5772...}}. Kaitan antara deret harmonik dan logaritma natural membantu dalam menganalisis kinerja algoritma seperti ''[[quicksort]]''.<ref>{{Citation|last1=Havil|first1=Julian|title=Gamma: Exploring Euler's Constant|publisher=[[Princeton University Press]]|isbn=978-0-691-09983-5|year=2003}}, bagian 11.5 dan 13.8</ref> |
|||
=== Transendensi logaritma === |
|||
Bilangan real yang bukan merupakan [[bilangan aljabar]] disebut bilangan transendental<ref>{{citation|title=Selected papers on number theory and algebraic geometry|volume=172|first1=Katsumi|last1=Nomizu|location=Providence, RI|publisher=AMS Bookstore|year=1996|isbn=978-0-8218-0445-2|page=21|url={{google books |plainurl=y |id=uDDxdu0lrWAC|page=21}}}}</ref>. Sebagai contoh, {{math|1=[[Pi|''{{pi}}'']]}} dan {{math|1=''[[E (konstanta matematika)|e]]}}'' adalah bilangan transendental, sedangkan <math>\sqrt{2-\sqrt 3}</math> bukan. Hampir semua [[bilangan real]] adalah [[Bilangan transendental|transendental]]. Logaritma merupakan sebuah contoh [[fungsi transendental]]. [[Teorema Gelfond–Schneider]] mengatakan bahwa logaritma biasanya memberikan nilai transendental.<ref>{{Citation|last1=Baker|first1=Alan|title=Transcendental number theory|publisher=[[Cambridge University Press]]|isbn=978-0-521-20461-3|year=1975}}, hlm. 10</ref> |
|||
== Perhitungan == |
|||
[[Berkas:Logarithm keys.jpg|jmpl|Tombol logaritma (LOG sebagai bilangan pokok 10 dan LN sebagai bilangan pokok {{mvar|e}}) pada sebuah kalkulator grafik [[TI-83 series|TI-83 Plus]].]] |
|||
Logaritma merupakan alat hitung yang mudah pada beberapa kasus, seperti {{math|1=<sup>10</sup>log 1000 = 3}}. Logaritma pada umumnya dapat dihitung melalui [[deret kuasa]] atau [[rata-rata aritmetika–geometrik]], atau didapatkan kembali dari tabel logaritma (sebelum adanya perhitungan logaritma) yang menyediakan ketepatan nilai konstan.<ref>{{Citation|last1=Muller|first1=Jean-Michel|title=Elementary functions|publisher=Birkhäuser Boston|location=Boston, MA|edition=2nd|isbn=978-0-8176-4372-0|year=2006}}, bagian 4.2.2 (hlm. 72) dan 5.5.2 (hlm. 95)</ref><ref>{{Citation|last1=Hart|last2=Cheney|last3=Lawson|year=1968|publisher=John Wiley|location=New York|title=Computer Approximations|series=SIAM Series in Applied Mathematics|display-authors=etal}}, bagian 6.3, hlm. 105–11</ref> [[Metode Newton]], sebuah metode berulang yang menyelesaikan persamaan melalui hampiran, juga dapat dipakai untuk menghitung logaritma, karena fungsi inversnya (yaitu fungsi eksponensial), dapat dihitung dengan cepat.<ref>{{Citation|last1=Zhang|first1=M.|last2=Delgado-Frias|first2=J.G.|last3=Vassiliadis|first3=S.|title=Table driven Newton scheme for high precision logarithm generation|doi=10.1049/ip-cdt:19941268|journal=IEE Proceedings - Computers and Digital Techniques|issn=1350-2387|volume=141|year=1994|issue=5|pages=281–92}}, bagian 1 for an overview</ref> Dengan melihat tabel logaritma, metode yang mirip dengan [[CORDIC]] dapat dipakai untuk menghitung logaritma hanya dengan menggunakan operasi penambahan dan [[Geseran aritmetika|geseran bit]].<ref>{{Citation|url=https://semanticscholar.org/paper/b3741168ba25f23b694cf8f9c80fb4f2aabce513|first=J.E.|last=Meggitt|title=Pseudo Division and Pseudo Multiplication Processes|journal=IBM Journal of Research and Development|date=April 1962|doi=10.1147/rd.62.0210|volume=6|issue=2|pages=210–26|s2cid=19387286}}</ref><ref>{{Citation|last=Kahan|first=W.|author-link=William Kahan|title=Pseudo-Division Algorithms for Floating-Point Logarithms and Exponentials|date=20 May 2001}}</ref> Terlebih lagi, [[Logaritma biner#Algoritma|algoritma dari logaritma biner]] menghitung {{math|lb(''x'')}} [[Rekursi|secara berulang]] berdasarkan penguadratan {{mvar|x}} yang berulang dan menggunakan ekspresi |
|||
: <math>^2\!\log\left(x^2\right) = 2 \cdot \, ^2\!\log |x|.</math> |
|||
=== Deret pangkat === |
|||
==== Deret Taylor ==== |
|||
[[Berkas:Taylor approximation of natural logarithm.gif|al=An animation showing increasingly good approximations of the logarithm graph.|jmpl|Deret Taylor dari {{math|ln(''z'')}} berpusat di {{math|''z'' {{=}} 1}}. Animasi berikut memperlihatkan 10 hampiran pertama beserta dengan hampiran yang ke-99 dan yang ke-100. Hampiran tersebut tidak konvergen karena melebihi jarak 1 dari pusatnya.]] |
|||
Untuk setiap bilangan {{mvar|z}} yang memenuhi sifat {{math|0 < ''z'' ≤ 2}}, maka berlaku rumus:{{refn|Deret yang sama berlaku untuk nilai utama dari logaritma kompleks untuk bilangan kompleks {{mvar|z}} yang memenuhi {{math|{{!}}''z'' − 1{{!}} < 1}}.|group=nb}}<ref name="AbramowitzStegunp.68">{{Harvard citations|editor1-last=Abramowitz|editor2-last=Stegun|year=1972|nb=yes|loc=hlm. 68}}</ref> |
|||
: <math> |
|||
\begin{align}\ln (z) &= \frac{(z-1)^1}{1} - \frac{(z-1)^2}{2} + \frac{(z-1)^3}{3} - \frac{(z-1)^4}{4} + \cdots \\ |
|||
&= \sum_{k=1}^\infty (-1)^{k+1}\frac{(z-1)^k}{k} |
|||
\end{align} |
|||
</math> |
|||
Pernyataan di atas merupakan tulisan singkat untuk mengatakan bahwa {{math|ln(''z'')}} dapat diaproksimasi sebagai bilangan yang lebih-lebih akurat lagi melalui ekspresi berikut: |
|||
: <math> |
|||
\begin{array}{lllll} |
|||
(z-1) & & \\ |
|||
(z-1) & - & \frac{(z-1)^2}{2} & \\ |
|||
(z-1) & - & \frac{(z-1)^2}{2} & + & \frac{(z-1)^3}{3} \\ |
|||
\vdots & |
|||
\end{array} |
|||
</math> |
|||
Sebagai contoh, pendekatan ketiga saat {{math|''z'' {{=}} 1,5}} memberikan nilai 0,4167. Nilai tersebut kira-kira 0,011 lebih besar dari {{math|ln(1,5) {{=}} 0,405465}}. [[Deret (matematika)|Deret]] ini yang mengaproksimasi {{math|ln(''z'')}} dengan ketepatan nilai sembarang, menyediakan jumlah dari nilai yang dijumlahkan cukup besar. Dalam kalkulus elementer, {{math|ln(''z'')}} adalah [[limit]] dari deret ini dan juga merupakan [[deret Taylor]] dari [[logaritma alami]] di {{math|1=''z'' = 1}}. Deret Taylor dari {{math|ln(''z'')}} khususnya menyediakan alat yang berguna untuk mengaproksimasi {{math|ln(1 + ''z'')}} ketika {{mvar|z}} bernilai kecil, {{math|{{!}}''z''{{!}} < 1}}: |
|||
: <math> |
|||
\ln (1+z) = z - \frac{z^2}{2} +\frac{z^3}{3}\cdots \approx z. |
|||
</math> |
|||
Sebagai contoh, hampiran orde pertama memberikan nilai hampiran {{math|ln(1,1) ≈ 0,1}} ketika {{math|1=''z'' = 0,1}}, yang galatnya 5% lebih kecil dari nilai eksak 0,0953. |
|||
==== Deret lebih efisien ==== |
|||
Deret lainnya berasal dari [[Fungsi hiperbolik invers#Fungsi tangen hiperbolik invers|fungsi tangen hiperbolik invers]]: |
|||
: <math> |
|||
\ln (z) = 2\cdot\operatorname{artanh}\,\frac{z-1}{z+1} = 2 \left (\frac{z-1}{z+1} + \frac{1}{3}{\left(\frac{z-1}{z+1}\right)}^3 + \frac{1}{5}{\left(\frac{z-1}{z+1}\right)}^5 + \cdots \right), |
|||
</math> |
|||
untuk setiap bilangan real {{math|''z'' > 0}}.{{refn|Deret yang sama berlaku untuk nilai utama dari logaritma kompleks untuk bilangan kompleks {{mvar|z}} dengan bagian real positif.|group=nb}}<ref name="AbramowitzStegunp.68" /> Dengan menggunakan [[notasi Sigma]], ruas kanan pada rumus di atas juga dapat ditulis sebagai |
|||
: <math>\ln (z) = 2\sum_{k=0}^\infty\frac{1}{2k+1}\left(\frac{z-1}{z+1}\right)^{2k+1}.</math> |
|||
Deret ini dapat diturunkan dari deret Taylor di atas, yang konvergen lebih cepat daripada deret Taylor, khususnya jika {{mvar|z}} mendekati 1. Sebagai contoh, untuk {{math|1=''z'' = 1,5}}, tiga suku pertama dari deret kedua memberikan nilai hampiran {{math|ln(1,5)}} dengan galatnya sekitar {{val|3|e=-6}}. Kekonvergenan cepat untuk {{mvar|z}} yang mendekati 1 dapat dimanfaatkan sebagai berikut: diberikan sebuah hampiran dengan tingkat akurat yang rendah {{math|''y'' ≈ ln(''z'')}} dan memasukkan ke rumus |
|||
: <math>A = \frac z{\exp(y)},</math> |
|||
maka logaritma dari {{mvar|z}} dirumuskan: |
|||
: <math>\ln (z)=y+\ln (A).</math> |
|||
Hampiran awalan {{mvar|y}} yang lebih baik adalah dengan membuat nilai {{mvar|A}} mendekati ke 1, sehingga nilai logaritma dapat dihitung lebih efisien. Nilai {{mvar|A}} dapat dihitung melalui [[Fungsi eksponensial|deret eksponensial]] sehingga nilainya konvergen dengan cepat, asalkan nilai {{mvar|y}} tidak terlalu besar. Dengan menghitung logaritma dari {{mvar|z}} yang lebih besar dapat direduksi menjadi nilai {{mvar|z}} yang lebih kecil dengan menulis {{math|''z'' {{=}} ''a'' · 10<sup>''b''</sup>}}, sehingga {{math|ln(''z'') {{=}} ln(''a'') + {{mvar|b}} · ln(10)}}. |
|||
Terdapat metode yang sangat berkaitan dengannya dapat dipakai untuk menghitung logaritma dari bilangan bulat. Dengan memasukkan <math>\textstyle z=\frac{n+1}{n}</math> pada deret di atas, maka deret tersebut dapat ditulis sebagai berikut: |
|||
: <math>\ln (n+1) = \ln(n) + 2\sum_{k=0}^\infty\frac{1}{2k+1}\left(\frac{1}{2 n+1}\right)^{2k+1}.</math> |
|||
Jika diketahui logaritma dari suatu bilangan bulat {{mvar|n}} yang lebih besar, maka deret tersebut menghasilkan sebauah deret yang konvergen dengan cepat untuk {{math|log(''n''+1)}}, dengan [[laju konvergensi]] dari <math display="inline">\left(\frac{1}{2 n+1}\right)^{2}</math>. |
|||
=== Hampiran purata aritmetika-geometrik === |
|||
[[Purata aritmetika–geometrik]] atau [[rata-rata aritmetika–geometrik]] menghasilkan hampiran dari [[logaritma natural]] dengan tingkatan ketepatan yang tinggi. Pada tahun 1982, Sasaki dan Kanada memperlihatkan bahwa purata ini sangat cepat untuk ketepatan di antara 400 dan 1000 letak desimal, sementara metode deret Taylor biasanya lebih cepat ketika membutuhkan nilai yang kurang akurat. Dalam karyanya, {{math|ln(''x'')}} kira-kira sama dengan ketepatan dari {{math|2<sup>−''p''</sup>}} (atau {{Mvar|p}} bit yang tepat) melalui rumus berikut (karena [[Carl Friedrich Gauss]]):<ref>{{Citation|first1=T.|last1=Sasaki|first2=Y.|last2=Kanada|title=Practically fast multiple-precision evaluation of log(x)|journal=Journal of Information Processing|volume=5|issue=4|pages=247–50|year=1982|url=http://ci.nii.ac.jp/naid/110002673332|access-date=30 Maret 2011}}</ref><ref>{{Citation|first1=Timm|title=Stacs 99|last1=Ahrendt|publisher=Springer|location=Berlin, New York|series=Lecture notes in computer science|doi=10.1007/3-540-49116-3_28|volume=1564|year=1999|pages=302–12|isbn=978-3-540-65691-3|chapter=Fast Computations of the Exponential Function}}</ref> |
|||
: <math>\ln (x) \approx \frac{\pi}{2\, \mathrm{M}\!\left(1, 2^{2 - m}/x \right)} - m \ln(2).</math> |
|||
Notasi {{math|M(''x'', ''y'')}} menyatakan [[rata-rata aritmetika–geometrik]] dari {{mvar|x}} dan {{mvar|y}}. Purata ini didapatkan dengan menghitung rerata {{Math|(''x'' + ''y'')/2}} ([[purata aritmetika]]) dan <math display="inline">\sqrt{xy}</math> ([[purata geometrik]]) dari {{mvar|x}} dan {{mvar|y}} secara berulang, lalu misalkan kedua bilangan tersebut merupakan bilangan {{mvar|x}} dan {{mvar|y}} selanjutnya. Kedua bilangan tersebut konvergen dengan cepat menuju ke limit yang sama, yaitu {{math|M(''x'', ''y'')}}. Agar pasti bahwa nilai yang diperlukan tepat, maka pilih {{mvar|m}} sehingga |
|||
: <math>x \,2^m > 2^{p/2}.\, </math> |
|||
Bilangan {{mvar|m}} yang lebih besar membuat perhitungan {{math|M(''x'', ''y'')}}, dengan nilai awal {{mvar|x}} dan {{mvar|y}} yang merupakan nilai yang sangat jauh, mengambil langkah lebih lanjut agar nilainya konvergen, tetapi memberikan nilai yang lebih tepat. Konstanta seperti {{math|{{pi}}}} dan {{math|ln(2)}} dapat dihitung melalui deret yang konvergen dengan cepat. |
|||
=== Algoritma Feynman === |
|||
[[Richard Feynman]], yang mengerjakan [[proyek Manhattan]] di [[Los Alamos National Laboratory]], mengembangkan sebuah algoritma pengolahan bit untuk menghitung nilai logaritma. Algoritma tersebut menyerupai pembagian panjang, dan kemudian dipakai dalam sebuah anggota dari rangkaian subkomputer, [[Connection Machine]]. Bahkan bahwa setiap bilangan real {{Math|1 < ''x'' < 2}} yang dapat direpresentasikan sebagai hasil kali dari faktor yang berbeda dari bentuk {{Math|1 + 2<sup>−''k''</sup>}}, dipakai dalam algoritma ini. Algoritma ini dibangun secara berurutan bahwa hasil kali {{Mvar|P}}, yang dimulai dengan {{math|''P'' {{=}} 1}} dan {{math|''k'' {{=}} 1}}, mengatakan bahwa jika {{math|''P'' · (1 + 2<sup>−''k''</sup>) < ''x''}}, maka {{Mvar|P}} berubah menjadi {{math|''P'' · (1 + 2<sup>−''k''</sup>)}}, sehingga membuat nilai <math>k</math> menaik. Algoritma tersebut berhenti ketika {{Mvar|k}} cukup besar memberikan nilai akurat yang diinginkan. Karena {{Math|log(''x'')}} adalah jumlah dari suku berbentuk {{Math|log(1 + 2<sup>−''k''</sup>)}} yang berpadanan dengan nilai {{Mvar|k}} dan faktor {{Math|1 + 2<sup>−''k''</sup>}} adalah hasil kali dari {{Mvar|P}}, maka {{Math|log(''x'')}} dapat dihitung melalui operasi penambahan yang sederhana, yaitu menggunakan tabel dari {{Math|log(1 + 2<sup>−''k''</sup>)}} untuk semua {{Mvar|k}}. Setiap bilangan pokok dapat dipakai untuk tabel logaritma.<ref>{{citation|first=Danny|last=Hillis|author-link=Danny Hillis|title=Richard Feynman and The Connection Machine|journal=Physics Today|volume=42|issue=2|page=78|date=15 January 1989|doi=10.1063/1.881196|bibcode=1989PhT....42b..78H}}</ref> |
|||
== Penerapan == |
|||
[[Berkas:NautilusCutawayLogarithmicSpiral.jpg|al=A photograph of a nautilus' shell.|jmpl|Sebuah cangkang [[nautilus]] yang menampilkan bentuk spiral logaritmik.]] |
|||
Logaritma memiliki banyak penerapan di dalam maupun di luar matematika. Ada beberapa kejadian penerapan logaritma yang berkaitan dengan gagasan [[kekararan skala]]. Sebagai contoh, setiap ruangan yang terdapat di dalam sebuah cangkang [[nautilus]] memiliki kira-kira sama dengan jumlah salinan dari ruang selanjutnya, yang ditimbang melalui faktor konstanta. Contoh tersebut menyerupai bentuk [[spiral logaritmik]].<ref>{{Harvard citations|last1=Maor|year=2009|nb=yes|loc=hlm. 135}}</ref> [[Hukum Benford]] mengenai distribusi dari angka yang ditunjuk juga dapat dijelaskan melalui kekeraran skala.<ref>{{Citation|last1=Frey|first1=Bruce|title=Statistics hacks|publisher=[[O'Reilly Media|O'Reilly]]|location=Sebastopol, CA|series=Hacks Series|url={{google books |plainurl=y |id=HOPyiNb9UqwC|page=275}}|isbn=978-0-596-10164-0|year=2006}}, bab 6, bagian 64</ref> Logaritma juga berkaitan dengan benda yang memiliki [[Kemiripan diri sendiri|kemiripan terhadap diri sendiri]]. Sebagai contoh, logaritma muncul dalam analisis tentang algoritma yang menyelesaikan masalah dengan membaginya menjadi dua masalah lebih kecil yang serupa dan memotong kecil penyelesaiannya.<ref>{{Citation|last1=Ricciardi|first1=Luigi M.|title=Lectures in applied mathematics and informatics|url={{google books |plainurl=y |id=Cw4NAQAAIAAJ}}|publisher=Manchester University Press|location=Manchester|isbn=978-0-7190-2671-3|year=1990}}, hlm. 21, bagian 1.3.2</ref> Dimensi dari bentuk geometrik menyerupai diri sendiri, dalam artian bahwa bentuk yang bagiannya menyerupai gambarnya secara keseluruhan juga dirumuskan melalui logaritma. [[Skala logaritmik]] berguna untuk mengukur perubahan relatif nilai daripada selisih mutlaknya. Terlebih lagi, karena fungsi logaritmik {{math|log(''x'')}} menaik sangat lambat untuk nilai besar{{mvar|x}}, skala logaritmik biasanya menekan data ilmiah yang berskala besar. Logaritma juga muncul dalam rumus ilmiah numerik, seperti [[persamaan roket Tsiolkovsky]], [[persamaan Fenske]], atau [[persamaan Nernst]]. |
|||
=== Penerapannya dalam skala logaritmik === |
|||
{{Main|Skala logaritmik}} |
|||
[[Berkas:Germany Hyperinflation.svg|al=Grafik yang menggambarkan nilai dari waktu ke waktu. Melalui skala logaritma, garis pada grafik memperlihatkan nilainya yang menaik dengan cepat.|jmpl|Grafik logaritma memperlihatkan kenaikan harga mata uang [[Mark Jerman|''goldmark'']] di [[Papiermark Jerman|Papiermark]] selama berlangsungnya [[Inflasi di Republik Weimar|hiperinflasi di Jerman pada tahun 1920-an]]|kiri]] |
|||
Satuan kuantitas dalam ilmiah seringkali dinyatakan sebagai logaritma dari kuantitas lain, dengan menggunakan ''skala logaritmik''. Sebagai contoh, [[desibel]] merupakan [[Satuan|satuan pengukuran]] yang dikaitkan dengan perhitungan dari [[Tingkatan (kuantitas logaritma)|kuantitas]] [[skala logaritmik]]. Penguat desibel memberikan 10 kalinya logaritma biasa dari [[rasio]] [[Daya (fisika)|daya]] atau 20 kalinya logaritma biasa dari rasio [[Tegangan listrik|tegangan]]. Satuan inilah yang dipakai untuk mengukur rugi tingkatan ketegangan saat mentransmisi sinyal elektrik,<ref>{{Citation|last1=Bakshi|first1=U.A.|title=Telecommunication Engineering|publisher=Technical Publications|location=Pune|isbn=978-81-8431-725-1|year=2009|url={{google books |plainurl=y |id=EV4AF0XJO9wC|page=A5}}}}{{Pranala mati|date=Februari 2023 |bot=InternetArchiveBot |fix-attempted=yes }}, bagian 5.2</ref> yang bertujuan untuk menjelaskan tingkatan kekuatan aras daya suara dalam [[akustik]],<ref>{{Citation|last1=Maling|first1=George C.|editor1-last=Rossing|editor1-first=Thomas D.|title=Springer handbook of acoustics|publisher=[[Springer-Verlag]]|location=Berlin, New York|isbn=978-0-387-30446-5|year=2007|chapter=Noise}}, bagian 23.0.2</ref> serta mengukur [[absorbansi|penyerapan]] cahaya dalam bidang [[Spektrometer|spektrometri]] dan [[optika]]. Selain itu, desibel juga dipakai dalam [[nisbah sinyal-derau]] yang menjelaskan seberapa banyak [[Derau (elektronik)|derau]] dibandingkan dengan [[Sinyal (elektrik)|sinyal]] yang berguna.<ref>{{Citation|last1=Tashev|first1=Ivan Jelev|title=Sound Capture and Processing: Practical Approaches|publisher=[[John Wiley & Sons]]|location=New York|isbn=978-0-470-31983-3|year=2009|url={{google books |plainurl=y |id=plll9smnbOIC|page=48}}|page=98}}</ref> Mirip dengan tadi, [[nisbah puncak sinyal terhadap derau|nisbah puncak sinyal-derau]] biasanya dipakai menilai kualitas suara dan metode [[pemampatan citra]] melalui logaritma.<ref>{{Citation|last1=Chui|first1=C.K.|title=Wavelets: a mathematical tool for signal processing|publisher=[[Society for Industrial and Applied Mathematics]]|location=Philadelphia|series=SIAM monographs on mathematical modeling and computation|isbn=978-0-89871-384-8|year=1997|url={{google books |plainurl=y |id=N06Gu433PawC|page=180}}}}</ref> |
|||
Kekuatan gempa bumi diukur dengan mengambil logaritma umum dari energi yang dipancarkan saat terjadinya gempa dalam satuan [[skala magnitudo momen]] atau [[skala Richter|skala magnitudo Ritcher]]. Sebagai contoh, gempa berkekuatan 5,0 melepaskan 32 kali {{math|(10<sup>1,5</sup>)}} dan gempa berkekuatan 6,0 melepaskan 1000 kali{{math|(10<sup>3</sup>)}} energi berkekuatan 4,0.<ref>{{Citation|last1=Crauder|first1=Bruce|last2=Evans|first2=Benny|last3=Noell|first3=Alan|title=Functions and Change: A Modeling Approach to College Algebra|publisher=Cengage Learning|location=Boston|edition=4th|isbn=978-0-547-15669-9|year=2008}}, bagian 4.4.</ref> Skala logaritmik juga dipakai dalam [[Magnitudo semu|magnitudo kentara]] untuk mengukur kecerahan bintang.<ref>{{Citation|last1=Bradt|first1=Hale|title=Astronomy methods: a physical approach to astronomical observations|publisher=[[Cambridge University Press]]|series=Cambridge Planetary Science|isbn=978-0-521-53551-9|year=2004}}, bagian 8.3, hlm. 231</ref> Dalam [[kimia]], negatif dari logaritma desimal, yang disebut sebagai '''{{vanchor|kologaritma}}''' desimal, ditunjukkan dengan huruf "p".<ref name="Jens">{{cite journal|author=Nørby, Jens|year=2000|title=The origin and the meaning of the little p in pH|journal=Trends in Biochemical Sciences|volume=25|issue=1|pages=36–37|doi=10.1016/S0968-0004(99)01517-0|pmid=10637613}}</ref> Sebagai contoh, [[pH]] merupakan kologaritma desimal dari [[Aktivitas termodinamika|keaktifan]] dari [[ion]] berbentuk [[hidrogen]] {{chem|H|+|}} yang terbentuk dari air, [[hidronium]].<ref>{{Citation|author=IUPAC|title=Compendium of Chemical Terminology ("Gold Book")|edition=2nd|editor=A. D. McNaught, A. Wilkinson|publisher=Blackwell Scientific Publications|location=Oxford|year=1997|url=http://goldbook.iupac.org/P04524.html|isbn=978-0-9678550-9-7|doi=10.1351/goldbook|author-link=IUPAC|doi-access=free}}</ref> Keaktifan dari ion hidronium dalam air yang netral bernilai 10<sup>−7</sup> [[Molaritas|mol·L<sup>−1</sup>]], sehingga nilai pH adalah 7. Contoh lainnya, nilai pH dari asam cuka biasanya sekitar 3. Perbedaan nilai sebesar 4 sesuai dengan rasio 10<sup>4</sup> berdasarkan aktivitasnya, yaitu nilai dari aktivitas ion hidronium cuka sekitar 10<sup>−3</sup> mol·L<sup>−1</sup>. |
|||
Konsep skala logaritmik dapat dipakai dalam grafik (log-linear) [[Plot semilog|semilog]] bertujuan untuk memberikan visual terkait satu sumbu, yang biasanya berupa sumbu vertikal, diukur menggunakan perhitungan logaritma. Contohnya seperti grafik disamping menjelaskan nilai yang menaik dengan tajam dari 1 juta hingga 1 triliun ke dalam ruang yang sama (pada sumbu vertikal) saat grafiknya menaik dari 1 hingga 1 juta. Pada grafik tersebut, [[fungsi eksponensial]] {{math|1=''f''(''x'') = ''a'' · ''b''{{i sup|''x''}}}} muncul sebagai garis lurus dengan [[kemiringan]] yang sama dengan logaritma dari {{mvar|b}}. Selain itu, skala logaritma yang dapat dipakai dalam [[grafik log-log]] untuk mengukur sumbu vertikal dan horizontal, sehingga menyebabkan fungsi {{math|1=''f''(''x'') = ''a'' · ''x''{{i sup|''k''}}}} digambarkan sebagai garis lurus yang mempunyai kemiringan yang sama dengan bilangan yang dipangkat dengan {{mvar|k}}, diterapkan pada saat memberikan visual dan menganalisis [[hukum pangkat]].<ref>{{Citation|last1=Bird|first1=J.O.|title=Newnes engineering mathematics pocket book|publisher=Newnes|location=Oxford|edition=3rd|isbn=978-0-7506-4992-6|year=2001}}, bagian 34</ref> |
|||
=== Penerapannya dalam psikologi === |
|||
Penerapan logaritma juga terdapat dalam beberapa hukum yang menjelaskan tentang [[Persepsi|persepsi manusia]].<ref>{{Citation|last1=Goldstein|first1=E. Bruce|title=Encyclopedia of Perception|url={{google books |plainurl=y |id=Y4TOEN4f5ZMC}}|publisher=Sage|location=Thousand Oaks, CA|series=Encyclopedia of Perception|isbn=978-1-4129-4081-8|year=2009}}, hlm. 355–56</ref><ref>{{Citation|last1=Matthews|first1=Gerald|title=Human Performance: Cognition, Stress, and Individual Differences|url={{google books |plainurl=y |id=0XrpulSM1HUC}}|publisher=Psychology Press|location=Hove|isbn=978-0-415-04406-6|year=2000}}, hlm. 48</ref> Sebagai contoh, [[hukum Hick]] menjelaskan kaitan logaritmik antara waktu saat orang mengambil keputusan beserta jumlah keputusan yang dimiliki.<ref>{{Citation|last1=Welford|first1=A.T.|title=Fundamentals of skill|publisher=Methuen|location=London|isbn=978-0-416-03000-6|oclc=219156|year=1968}}, hlm. 61</ref> Hukum lainnya adalah [[hukum Fitts]], yang memprediksi bahwa waktu yang diperlukan saat bergerak ke daerah target dengan cepat sama dengan fungsi logaritmik dari jarak dan ukuran target.<ref>{{Citation|author=Paul M. Fitts|date=June 1954|title=The information capacity of the human motor system in controlling the amplitude of movement|journal=Journal of Experimental Psychology|volume=47|issue=6|pages=381–91|pmid=13174710|doi=10.1037/h0055392|s2cid=501599|url=https://semanticscholar.org/paper/3087289229146fc344560478aac366e4977749c0}}, reprinted in {{Citation|journal=Journal of Experimental Psychology: General|volume=121|issue=3|pages=262–69|year=1992|pmid=1402698|url=http://sing.stanford.edu/cs303-sp10/papers/1954-Fitts.pdf|access-date=30 March 2011|title=The information capacity of the human motor system in controlling the amplitude of movement|author=Paul M. Fitts|doi=10.1037/0096-3445.121.3.262}}</ref> Dalam [[psikofisika]], [[hukum Weber–Fechner]] mengatakan kaitan logaritmik dengan [[Stimulus (psikologi)|stimulus]] dan [[Indra (fisiologi)|sensasi]] yang dirasakan, contohnya seperti saat orang sedang membawa berat benda yang sesungguhnya dengan yang dirasakan.<ref>{{Citation|last1=Banerjee|first1=J.C.|title=Encyclopaedic dictionary of psychological terms|publisher=M.D. Publications|location=New Delhi|isbn=978-81-85880-28-0|oclc=33860167|year=1994|url={{google books |plainurl=y |id=Pwl5U2q5hfcC|page=306}}|page=304}}</ref> (Namun, "hukum" ini kurang realistis dengan model belakangan ini, seperti [[hukum perpangkatan Stevens]].<ref>{{Citation|last1=Nadel|first1=Lynn|author1-link=Lynn Nadel|title=Encyclopedia of cognitive science|publisher=[[John Wiley & Sons]]|location=New York|isbn=978-0-470-01619-0|year=2005}}, lemmas ''Psychophysics'' and ''Perception: Overview''</ref>) |
|||
Studi psikologi menemukan bahwa orang yang sedikit mempunyai pemahaman matematika cenderung mengestimasi nilai kuantitas dengan logaritma, atau dengan kata lain, bilangannya ditempatkan pada garis yang tidak ditandai berdasarkan perhitungan logaritma, sehingga 10 yang ditempatkan mendekati 100 dianggap sebagai 100 yang ditempatkan mendekati 1000. Orang yang memiliki pemahaman yang lebih tinggi memandang hal tersebut sebagai linear yang mengestimasi (letak angka 1000 yang berjarak 10 kali lebih jauh) pada beberapa kasus, namun logaritma dipakai pada saat memplot bilangan-bilangan yang sulit untuk diplotkan secara linear.<ref>{{Citation|doi=10.1111/1467-9280.02438|last1=Siegler|first1=Robert S.|last2=Opfer|first2=John E.|title=The Development of Numerical Estimation. Evidence for Multiple Representations of Numerical Quantity|volume=14|issue=3|pages=237–43|year=2003|journal=Psychological Science|url=http://www.psy.cmu.edu/~siegler/sieglerbooth-cd04.pdf|pmid=12741747|citeseerx=10.1.1.727.3696|s2cid=9583202|access-date=7 January 2011|archive-url=https://web.archive.org/web/20110517002232/http://www.psy.cmu.edu/~siegler/sieglerbooth-cd04.pdf|archive-date=17 May 2011|url-status=dead}}</ref><ref>{{Citation|last1=Dehaene|first1=Stanislas|last2=Izard|first2=Véronique|last3=Spelke|first3=Elizabeth|last4=Pica|first4=Pierre|title=Log or Linear? Distinct Intuitions of the Number Scale in Western and Amazonian Indigene Cultures|volume=320|issue=5880|pages=1217–20|doi=10.1126/science.1156540|pmc=2610411|pmid=18511690|year=2008|journal=Science|bibcode=2008Sci...320.1217D|citeseerx=10.1.1.362.2390}}</ref> |
|||
=== Penerapannya dalam teori peluang dan statistika === |
|||
{{multiple image |
|||
| total_width = 500 |
|||
| image1 = PDF-log_normal_distributions.svg |
|||
| alt1 = Tiga kurva fungsi kepadatan probabilitas yang asimetrik |
|||
| caption1 = Tiga [[fungsi kepekatan probabilitas|fungsi kepadatan probabilitas]] (PDF) dari variabel acak dengan sebaran log-normal. Parameter lokasi {{math|μ}} yang bernilai nol untuk semua tiga fungsi tersebut, merupakan purata logaritma dari variabel acak, bukan purata dari variabel tersendiri. |
|||
| image2 = Benfords_law_illustrated_by_world's_countries_population.png |
|||
| alt2 = A bar chart and a superimposed second chart. The two differ slightly, but both decrease in a similar fashion |
|||
| caption2 = Sebaran digit pertama (dalam bentuk persentase, dengan batang berwarna merah) dalam [[Daftar negara menurut jumlah penduduk|jumlah populasi dari 237 negara]] di dunia. Titik berwarna hitam menunjukkan sebaran yang diprediksi menurut hukum Benford. |
|||
| direction = horizontal |
|||
}} |
|||
Dalam [[teori probabilitas]], [[hukum bilangan besar]] mengatakan bahwa, untuk sebuah [[mata uang seimbang]], ketika jumlah pelemparan koin naik menuju takhingga, maka kesebandingan dari gambar kepala (atau ekor) yang diamati [[Distribusi binomial|mendekati satu setengah]]. Fluktuasi dari nilai kesebandingan yang bernilai satu setengah dijelaskan melalui hukum yang menggunakan logaritma, yaitu [[hukum logaritma teriterasi]].<ref>{{Citation|last1=Breiman|first1=Leo|title=Probability|publisher=[[Society for Industrial and Applied Mathematics]]|location=Philadelphia|series=Classics in applied mathematics|isbn=978-0-89871-296-4|year=1992}}, bagian 12.9</ref> |
|||
Logaritma muncul pula dalam [[sebaran log-normal]]. Ketika logaritma dari [[variabel acak]] mempunyai [[Distribusi normal|sebaran normal]], maka variabel dikatakan mempunyai sebaran log-normal.<ref>{{Citation|last1=Aitchison|first1=J.|last2=Brown|first2=J.A.C.|title=The lognormal distribution|publisher=[[Cambridge University Press]]|isbn=978-0-521-04011-2|oclc=301100935|year=1969}}</ref> Sebaran log-normal ditemukan dalam banyak bidang, dengan suatu variabel dibentuk sebagai hasil kali dari banyaknya variabel acak indenpenden bernilai positif. Contohnya seperti dalam mempelajari turbulensi.<ref>{{Citation|title=An introduction to turbulent flow|author=Jean Mathieu and Julian Scott|publisher=Cambridge University Press|year=2000|isbn=978-0-521-77538-0|page=50|url={{google books |plainurl=y |id=nVA53NEAx64C|page=50}}}}</ref> |
|||
Logaritma dipakai untuk menghitung [[pendugaan kemungkinan maksimum|estimasi kemungkinan maksimum]] dari [[model statistika]] parametrik. [[Fungsi kemungkinan]] pada model tersebut bergantung setidaknya satu [[model parametrik|parameter]] yang harus diestimasi. Nilai maksimum dari fungsi kemungkinan muncul di nilai parameter yang sama sebagai nilai maksimum logaritma kemungkinan (atau disebut ''log likelihood''), karena logaritma merupakan fungsi menaik. ''Log-likelihood'' adalah teknik yang memaksimumkan fungsi dengan mudah, khususnya untuk kemungkinan yang dikali mengenai variabel acak [[Independen (peluang)|independen]].<ref>{{Citation|last1=Rose|first1=Colin|last2=Smith|first2=Murray D.|title=Mathematical statistics with Mathematica|publisher=[[Springer-Verlag]]|location=Berlin, New York|series=Springer texts in statistics|isbn=978-0-387-95234-5|year=2002}}, bagian 11.3</ref> |
|||
[[Hukum Benford]] menjelaskan kemungkinan digit dalam [[himpunan data]] yang banyak, contohnya seperti tinggi bangunan. Menurut hukum Benford, kemungkinan bahwa digit desimal pertama suatu item dalam sampel data adalah {{Mvar|d}} (yang berkisar dari 1 hingga 9) sama dengan {{math|<sup>10</sup>log (''d'' + 1) − <sup>10</sup>log (''d'')}}, ''tanpa memperhatikan'' satuan pengukuran.<ref>{{Citation|last1=Tabachnikov|first1=Serge|author-link1=Sergei Tabachnikov|title=Geometry and Billiards|publisher=[[American Mathematical Society]]|location=Providence, RI|isbn=978-0-8218-3919-5|year=2005|pages=36–40}}, bagian 2.1</ref> Jadi, sekitar 30% data dapat diduga mempunyai 1 sebagai digit pertama, 18% dimulai dengan 2, dst. Penyimpangan dari hukum Benford dihitung oleh para akuntan untuk membantu mendeteksi penipuan data akuntansi.<ref>{{citation|title=The Effective Use of Benford's Law in Detecting Fraud in Accounting Data|first1=Cindy|last1=Durtschi|first2=William|last2=Hillison|first3=Carl|last3=Pacini|url=http://faculty.usfsp.edu/gkearns/Articles_Fraud/Benford%20Analysis%20Article.pdf|volume=V|pages=17–34|year=2004|journal=Journal of Forensic Accounting|archive-url=https://web.archive.org/web/20170829062510/http://faculty.usfsp.edu/gkearns/Articles_Fraud/Benford%20Analysis%20Article.pdf|archive-date=29 Agustus 2017|access-date=28 Mei 2018}}</ref> |
|||
=== Penerapannya dalam kompleksitas perhitungan === |
|||
Cabang dalam [[ilmu komputer]] yang mempelajari [[kompleksitas waktu|performa]] dari suatu [[algoritma]] dalam menyelesaikan persoalan atau masalah tertentu disebut [[analisis algoritma]].<ref name="Wegener">{{Citation|last1=Wegener|first1=Ingo|title=Complexity theory: exploring the limits of efficient algorithms|publisher=[[Springer-Verlag]]|location=Berlin, New York|isbn=978-3-540-21045-0|year=2005}}, hlm. 1–2</ref> Logaritma sangat penting dalam menjelaskan algoritma tersebut dengan [[Divide and Conquer|membagi suatu masalah]] menjadi lebih kecil, serta menghubungkan penyelesaian dari submasalah.<ref>{{Citation|last1=Harel|first1=David|last2=Feldman|first2=Yishai A.|title=Algorithmics: the spirit of computing|location=New York|publisher=[[Addison-Wesley]]|isbn=978-0-321-11784-7|year=2004}}, hlm. 143</ref> |
|||
Sebagai contoh, cara [[algoritma pencarian biner]] ({{lang-en|1=binary searching algorithm}}) dalam mencari bilangan dalam daftar yang tersortir adalah dengan memeriksa entri tengah dan meneruskannya di sebagian sebelum atau sesudah entri tengah jika tidak ditemukan bilangannya. Umumnya, algoritma ini memerlukan perbandingan {{math|<sup>2</sup>log (''N'')}}, dengan {{mvar|N}} adalah panjang daftar.<ref>{{citation|last=Knuth|first=Donald|author-link=Donald Knuth|title=The Art of Computer Programming|publisher=Addison-Wesley|location=Reading, MA|year=1998|isbn=978-0-201-89685-5|title-link=The Art of Computer Programming}}, bagian 6.2.1, hlm. 409–26</ref> Mirip dengan sebelumnya, algoritma [[urut gabung]]an menyortir daftar yang belum tersortir dengan membagi daftar menjadi setengah bagian dan mengurutkan daftar-daftar tersebut dahulu sebelum menggabungkan hasilnya. Algoritma urut gabungan biasanya memerlukan waktu yang [[Notasi O besar|kira-kira sebanding dengan]] {{math|''N'' · log(''N'')}}.<ref>{{Harvard citations|last=Knuth|first=Donald|year=1998|loc=bagian 5.2.4, hlm. 158–68|nb=yes}}</ref> Bilangan pokok logaritma tidak dijelaskan secara spesifik, karena hasilnya hanya berubah oleh faktor konstanta saat ada bilangan pokok lain yang sedang dipakai. Faktor konstanta biasanya diabaikan dalam analisis algoritma dalam [[Analisis algoritma#Model biaya|model biaya seragam]] ({{lang-en|1=uniform cost model}}) yang standar.<ref name="Wegener20">{{Citation|last1=Wegener|first1=Ingo|title=Complexity theory: exploring the limits of efficient algorithms|publisher=[[Springer-Verlag]]|location=Berlin, New York|isbn=978-3-540-21045-0|year=2005|page=20}}</ref> |
|||
Suatu fungsi {{math|''f''(''x'')}} dikatakan [[pertumbuhan logaritmik|bertumbuh secara logaritmik]] jika {{math|''f''(''x'')}} (setidaknya atau kira-kira) sebanding dengan logaritma dari {{mvar|x}}, namun istilah ini dipakai sebagai fungsi eksponensial dalam menjelaskan pertumbuhan organisme secara biologis.<ref>{{Citation|last1=Mohr|first1=Hans|last2=Schopfer|first2=Peter|title=Plant physiology|publisher=Springer-Verlag|location=Berlin, New York|isbn=978-3-540-58016-4|year=1995|url-access=registration|url=https://archive.org/details/plantphysiology0000mohr}}, bab 19, hlm. 298</ref> Sebagai contoh, setiap [[bilangan asli]] {{mvar|N}} dapat direpresentasikan dalam [[sistem bilangan biner|bentuk bilangan biner]] yang tidak lebih dari {{math|<sup>2</sup>log ''N'' + 1}} [[bit]]. Dengan kata lain, jumlah [[Memori (komputer)|memori]] diperlukan untuk menyimpan {{mvar|N}} pertumbuhan secara logaritmik dengan {{mvar|N}}. |
|||
=== Penerapannya dalam entropi dan ketidakteraturan === |
|||
[[Berkas:Chaotic Bunimovich stadium.png|thumb|al=Trayektori dua partikel berbentuk oval|[[Biliar dinamis|Bola biliar]] di atas meja biliar oval. Dua partikel yang bermula pada pusat meja dengan sudut luncur yang berbeda satu derajat, akan memiliki jalur yang amat berbeda karena [[Refleksi|pemantulan]] pada pinggir meja biliar]] |
|||
[[Entropi]] secara umum adalah ukuran dari ketidakteraturan dari suatu sistem. Dalam [[termodinamika statistik]], sebuah entropi, disimbolkan dengan {{Math|''S''}}, dari sebuah sistem, didefinisikan dengan: |
|||
: <math> S = - k \sum_i p_i \ln(p_i).\, </math> |
|||
Hasilnya adalah seluruh kondisi {{Mvar|i}} yang mungkin dari sistem yang dimaksud, contoh posisi dari partikel gas di dalam sebuah tangki. Lebih lanjut lagi, {{math|''p''<sub>''i''</sub>}} adalah kemungkinan bahwa kondisi {{Mvar|i}} telah tercapai dan {{mvar|k}} adalah [[konstanta Boltzmann]]. Sama halnya dengan [[Entropi (teori informasi)|entropi dalam teori informasi]] yang mengukur kuantitas dari informasi. Jika penerima pesan mengharapkan sejumlah {{mvar|N}} pesan yang mungkin diterima dengan besar kemungkinan masing-masing yang setara, maka sejumlah informasi yang tersampaikan oleh pesan tersebut dapat dikuantifikasi dengan bit {{math|<sup>2</sup>log ''N''}}.<ref>{{Citation|last1=Eco|first1=Umberto|author1-link=Umberto Eco|title=The open work|publisher=[[Harvard University Press]]|isbn=978-0-674-63976-8|year=1989}}, bagian III.I</ref> |
|||
[[Eksponen Lyapunov]] menggunakan logaritma untuk mengukur derajat ketidakteraturan dari sistem yang dinamis. Contoh partikel yang bergerak di meja biliar oval, di mana bahkan perubahan sekecil apapun dari kondisi awal dapat memberikan hasil, yaitu jalur yang dilalui, yang sangat berbeda. Sistem yang dimaksud disebut dengan [[teori chaos|kekacauan]] di dalam [[sistem deterministik]] karena galat yang kecil namun terukur dari kondisi awal dapat diprediksi akan memberikan hasil akhir yang sangat berbeda.<ref>{{Citation|last1=Sprott|first1=Julien Clinton|title=Elegant Chaos: Algebraically Simple Chaotic Flows|journal=Elegant Chaos: Algebraically Simple Chaotic Flows. Edited by Sprott Julien Clinton. Published by World Scientific Publishing Co. Pte. Ltd|url={{google books |plainurl=y |id=buILBDre9S4C}}|publisher=[[World Scientific]]|location=New Jersey|isbn=978-981-283-881-0|year=2010|bibcode=2010ecas.book.....S|doi=10.1142/7183}}, bagian 1.9</ref> Setidaknya satu eksponen Lyapunov dari sistem kekacauan yang deterministik akan bernilai positif. |
|||
=== Penerapannya dalam bangunan fraktal === |
|||
[[Berkas:Sierpinski dimension.svg|al=Parts of a triangle are removed in an iterated way.|ka|jmpl|400x400px|Segitiga Sierpinski (di sebelah kanan) dibangun dengan menggantikan [[segitiga sama sisi]] secara berulang dengan tiga salinan dirinya yang lebih kecil.]] |
|||
Logaritma muncul dalam definiisi [[Dimensi fraktal|dimensi]] [[fraktal]].<ref>{{Citation|last1=Helmberg|first1=Gilbert|title=Getting acquainted with fractals|publisher=Walter de Gruyter|series=De Gruyter Textbook|location=Berlin, New York|isbn=978-3-11-019092-2|year=2007}}</ref> Fraktal merupakan benda-benda geometri yang menyerupai dirinya, dalam artian bahwa benda geometri tersebut mereproduksi dirinya lebih kecil, penjelasan kasarnya, di seluruh strukturnya. Contohnya seperti [[segitiga Sierpiński]], dengan [[dimensi Hausdorff]]<nowiki/>nya adalah {{math|{{sfrac|1=ln(3)|2=ln(2)}} ≈ 1,58}}, dapat diliputi dengan tiga salinan dirinya, masing-masing sisinya dibagi menjadi setengah dari panjang awalnya. Adapula gagasan dimensi fraktal berdasarkan logaritma lainnya diperoleh dengan [[Dimensi menghitung kotak|menghitung jumlah kotak]] yang diperlukan untuk meliputi frakal dalam himpunan. |
|||
=== Penerapannya dalam musik === |
|||
{{multiple image |
|||
| direction = vertical |
|||
| width = 350 |
|||
| footer = Empat oktaf yang berbeda diperlihatkan pada skala linear, lalu diperlihatkan pada skala logaritmik (saat mendengarkannya dengan menggunakan telinga). |
|||
| image1 = 4Octaves.and.Frequencies.svg |
|||
| alt1 = Empat oktaf yang berbeda diperlihatkan pada skala linear. |
|||
| image2 = 4Octaves.and.Frequencies.Ears.svg |
|||
| alt2 = Empat oktaf yang berbeda diperlihatkan pada skala logaritmik. |
|||
}} |
|||
Logaritma berkaitan dengan bunyi nada dan [[Interval (musik)|interval]] dalam musik. Dalam [[temperamen sama]], perbandingan frekuensi bergantung pada interval di antara dua nada saja, bukan pada frekuensi yang spesifik atau [[tinggi nada|tinggi]] dari nada tunggal. Sebagai contoh, nada [[A (not musik)|''A'']] mempunyai frekuensi 440 [[Hertz|Hz]] dan [[B♭ (not musik)|''B-flat'']] mempunyai frekuensi 466 Hz. Interval antara nada ''A'' dengan ''B-flat'' ini digolongkan sebagai [[semi-nada]], karena intervalnya berada di antara ''B-flat'' dan [[B (not musik)|''B'']] (yang mempunyai frekuensi 493 Hz). Maka, perbandingan frekuensinya adalah: |
|||
: <math>\frac{466}{440} \approx \frac{493}{466} \approx 1,059 \approx \sqrt[12]2.</math> |
|||
Peran logaritma dalam musik dapat dipakai untuk menjelaskan interval berikut: suatu interval diukur dalam semi-nada dengan mengambil logaritma dengan {{Nowrap|bilangan pokok-{{math|2<sup>1/12</sup>}}}} dari perbandingan [[frekuensi]], sedangkan logaritma dengan {{Nowrap|bilangan pokok-{{math|2<sup>1/1200</sup>}}}} dari perbandingan frekuensi menyatakan interval dalam [[Sen (musik)|sen]], ratusan semi-nada. Logaritma yang terakhir dipakai untuk pengodean yang lebih halus, karena diperlukan untuk temperamen tak sama.<ref>{{Citation|last1=Wright|first1=David|title=Mathematics and music|location=Providence, RI|publisher=AMS Bookstore|isbn=978-0-8218-4873-9|year=2009}}, bab 5</ref> |
|||
{| class="wikitable" style="text-align:center; margin:1em auto 1em auto;" |
|||
|'''Interval''' (dua bunyi nada yang dimainkan dalam waktu yang sama) |
|||
|[[72 temperamen sama|Bunyi nada 1/12]] {{audio|1_step_in_72-et_on_C.mid|play}} |
|||
|[[Semi-nada]] {{audio|Minor_second_on_C.mid|play|help=no}} |
|||
|''[[Just major third]]'' {{audio|Just_major_third_on_C.mid|play|help=no}} |
|||
|''[[Major third]]'' {{audio|Major_third_on_C.mid|play|help=no}} |
|||
|''[[Tritone]]'' {{audio|Tritone_on_C.mid|play|help=no}} |
|||
|[[Oktaf]] {{audio|Perfect_octave_on_C.mid|play|help=no}} |
|||
|- |
|||
|'''Rasio frekuensi''' ''r'' |
|||
|<math>2^{\frac 1 {72}} \approx 1.0097</math> |
|||
|<math>2^{\frac 1 {12}} \approx 1.0595</math> |
|||
|<math>\tfrac 5 4 = 1.25</math> |
|||
|<math>\begin{align} 2^{\frac 4 {12}} & = \sqrt[3] 2 \\ & \approx 1.2599 \end{align} </math> |
|||
|<math>\begin{align} 2^{\frac 6 {12}} & = \sqrt 2 \\ & \approx 1.4142 \end{align} </math> |
|||
|<math> 2^{\frac {12} {12}} = 2 </math> |
|||
|- |
|||
|'''Jumlah semi-nada yang sama'''<math>^{\sqrt[12] 2}\!\log r = 12 \, ^2\!\log r</math> |
|||
|<math>\tfrac 1 6</math> |
|||
|<math>1</math> |
|||
|<math>\approx 3,8631</math> |
|||
|<math>4</math> |
|||
|<math>6</math> |
|||
|<math>12</math> |
|||
|- |
|||
|'''Jumlah sen yang sama'''<math>^{\sqrt[1200] 2}\!\log r = 1200 \, ^2\!\log r</math> |
|||
|<math>16 \tfrac 2 3</math> |
|||
|<math>100</math> |
|||
|<math>\approx 386,31</math> |
|||
|<math>400</math> |
|||
|<math>600</math> |
|||
|<math>1200</math> |
|||
|} |
|||
=== Penerapannya dalam teori bilangan === |
|||
[[Logaritma alami]] sangat berkaitan dengan salah satu topik dalam [[teori bilangan]], yaitu [[Fungsi pencacahan bilangan prima|menghitung bilangan prima]]. Untuk setiap [[bilangan bulat]] {{mvar|x}}, jumlah [[bilangan prima]] kurang dari sama dengan {{mvar|x}} dinyatakan sebagai {{math|[[fungsi pencacahan bilangan prima|{{pi}}(''x'')]]}}. [[Teorema bilangan prima]] mengatakan bahwa {{math|{{pi}}(''x'')}} kira-kira sama dengan |
|||
: <math>\frac{x}{\ln(x)},</math> |
|||
yang berarti bahwa fungsi pencacahan bilangan prima kira-kira sama dengan perbandingan dari {{math|{{pi}}(''x'')}} dan pecahan yang mendekati 1 ketika {{mvar|x}} menuju ke takhingga.<ref>{{Citation|last1=Bateman|first1=P.T.|last2=Diamond|first2=Harold G.|title=Analytic number theory: an introductory course|publisher=[[World Scientific]]|location=New Jersey|isbn=978-981-256-080-3|oclc=492669517|year=2004}}, teorema 4.1</ref> Akibatnya, peluang dari bilangan yang dipilih secara acak di antara 1 dan {{mvar|x}} adalah bilangan prima [[Kesebandingan (matematika)|berbanding]] terbalik dengan jumlah digit desimal {{mvar|x}}. Pendekatan {{math|{{pi}}(''x'')}} yang lebih baik merupakan [[Fungsi integral logaritmik|fungsi integral Euler]] {{math|Li(''x'')}}, yang didefinisikan sebagai |
|||
: <math> \mathrm{Li}(x) = \int_2^x \frac1{\ln(t)} \,dt. </math> |
|||
[[Hipotesis Riemann]], yang merupakan salah satu [[konjektur]] matemtika terbuka yang paling terlama, dapat dinyatakan dalam bentuk perbandingan {{math|{{pi}}(''x'')}} dan {{math|Li(''x'')}}.<ref>{{Harvard citations|last1=Bateman|first1=P. T.|last2=Diamond|year=2004|nb=yes|loc=Teoerma 8.15}}</ref> [[Teorema Erdős–Kac]] mengatakan bahwa jumlah [[Bilangan prima#Faktorisasi unik|faktor bilangan prima]] yang berbeda juga melibatkan [[logaritma alami]]. |
|||
Logaritma dari ''n'' [[faktorial]], {{math|1=''n''! = 1 · 2 · ... · ''n''}}, dirumuskan sebagai |
|||
: <math> \ln (n!) = \ln (1) + \ln (2) + \cdots + \ln (n).</math> |
|||
Rumus di atas dapat dipakai utnuk memperoleh sebuah hampiran dari {{math|''n''!}} untuk setiap bilangan {{mvar|n}} yang lebih besar, yaitu [[rumus Stirling]].<ref>{{Citation|last1=Slomson|first1=Alan B.|title=An introduction to combinatorics|publisher=[[CRC Press]]|location=London|isbn=978-0-412-35370-3|year=1991}}, bab 4</ref> |
|||
== Perumuman == |
|||
=== Logaritma kompleks === |
|||
{{Main|Logaritma kompleks}} |
|||
Semua [[bilangan kompleks]] {{mvar|a}} yang menyelesaikan persamaan |
|||
: <math>e^a=z</math> |
|||
disebut ''logaritma kompleks'' dari {{mvar|z}}, ketika {{mvar|z}} (dianggap sebagai) bilangan kompleks. Bilangan kompleks biasanya dinyatakan sebagai {{math|''z {{=}} x + iy''}}, dengan {{mvar|x}} dan {{mvar|y}} adalah bilangan real dan {{mvar|i}} adalah [[satuan imajiner]] (satuan yang dikuadratkan memberikan nilai −1). Bilangan kompleks dapat divisualisasikan melalui sebuah titik dalam [[bidang kompleks]], seperti yang diperlihatkan pada gambar berikut. [[Bilangan kompleks#Bidang kompleks polar|Bentuk polar]] menulis bilangan kompleks tak-nol {{mvar|z}} melalui titik [[nilai mutlak]], yang berarti jarak yang berupa bilangan bernilai real dan positif {{Mvar|r}} sama dengan titik {{mvar|z}} ke [[Titik nol|titik asalnya]]. Bentuk polar juga menulis sebuah sudut antara bilangan real pada sumbu-{{Math|Re}} (yakni sumbu-{{mvar|x}}) '' ''{{Math|Re}} dan garis yang melalui titik asal dan titik {{mvar|z}}. Sudut tersebut disebut sebagai [[Argumen (bilangan kompleks)|argumen]] dari {{mvar|z}}.[[Berkas:Complex number illustration multiple arguments.svg|al=Sebuah ilustrasi mengenai bentuk polar: sebuah titik yang dijelaskan melalui sebuah panah atau secara ekuivalen melalui panjang dan sudutnya ke sumbu-x.|jmpl|Bentuk polar dari {{math|''z {{=}} x + iy''}}. {{mvar|φ}} dan {{mvar|φ'}} adalah argumen dari {{mvar|z}}.]]Nilai mutlak {{mvar|r}} dari {{mvar|z}} dinyatakan sebagai |
|||
: <math>\textstyle r=\sqrt{x^2+y^2}.</math> |
|||
Dengan menggunakan pandangan geometris pada fungsi [[Sinus (trigonometri)|sinus]] dan [[kosinus]] beserta periodisitasnya dalam {{Math|2{{pi}}}}, setiap bilangan kompleks {{mvar|z}} dapat dinyatakan sebagai |
|||
: <math>z = x + iy = r (\cos \varphi + i \sin \varphi)= r (\cos (\varphi + 2k\pi) + i \sin (\varphi + 2k\pi)),</math> |
|||
untuk setiap bilangan bulat {{mvar|k}}. Nyatanya, argumen dari {{mvar|z}} tidak dijelaskan secara unik, yakni: bilangan {{mvar|φ}} dan {{Math|1=''φ''' = ''φ'' + 2''k''{{pi}}}} adalah argumen valid dari {{mvar|z}} untuk semua bilangan bulat {{mvar|k}}, karena menambahkan {{Math|2''k''{{pi}}}} [[radian]] atau ''k''⋅360°{{refn|Lihat [[radian]] untuk konversi antara 2[[pi|{{pi}}]] dengan 360 [[derajat (sudut)|derajat]].|group=nb}} ke bilangan {{mvar|φ}} berpadanan dengan "lilitan" di sekitar titik asal yang berputar berlawanan arah jarum jam sebanyak {{mvar|k}} [[Putaran (geometri)|putaran]]. Hasil bilangan kompleks selalu {{mvar|z}}, seperti yang diilustrasikan pada gambar untuk {{math|''k'' {{=}} 1}}. Setidaknya ada salah satu dari argumen {{mvar|z}} yang mungkin disebut sebagai ''argumen prinsip'', yang dilambangkan {{math|Arg(''z'')}}, dipilih dengan memerlukan putaran {{mvar|φ}} di [[Selang (matematika)|selang]] {{open-closed|−π, π}}<ref>{{Citation|last1=Ganguly|location=Kolkata|first1=S.|title=Elements of Complex Analysis|publisher=Academic Publishers|isbn=978-81-87504-86-3|year=2005}}, Definisi 1.6.3</ref> atau {{Math|[0, 2{{pi}})}}.<ref>{{Citation|last1=Nevanlinna|first1=Rolf Herman|author1-link=Rolf Nevanlinna|last2=Paatero|first2=Veikko|title=Introduction to complex analysis|journal=London: Hilger|location=Providence, RI|publisher=AMS Bookstore|isbn=978-0-8218-4399-4|year=2007|bibcode=1974aitc.book.....W}}, bagian 5.9</ref> Daerah-daerah tersebut, dengan argumen {{mvar|z}} ditentukan sekali disebut [[Cabang prinsip|''cabang'']] dari fungsi argumen. |
|||
[[Rumus Euler]] mengaitkan [[fungsi trigonometri]] [[Sinus (trigonometri)|sinus]] dan [[kosinus]] dengan [[Rumus Euler|eksponensial kompleks]]: |
|||
: <math>e^{i\varphi} = \cos \varphi + i\sin \varphi .</math> |
|||
Dengan menggunakan rumus di atas, dan periodisitasnya lagi, maka berlaku identitas berikut:<ref>{{Citation|last1=Moore|first1=Theral Orvis|last2=Hadlock|first2=Edwin H.|title=Complex analysis|publisher=[[World Scientific]]|location=Singapore|isbn=978-981-02-0246-0|year=1991}}, bagian 1.2</ref> |
|||
: <math> \begin{array}{lll}z& = & r \left (\cos \varphi + i \sin \varphi\right) \\ |
|||
& = & r \left (\cos(\varphi + 2k\pi) + i \sin(\varphi + 2k\pi)\right) \\ |
|||
& = & r e^{i (\varphi + 2k\pi)} \\ |
|||
& = & e^{\ln(r)} e^{i (\varphi + 2k\pi)} \\ |
|||
& = & e^{\ln(r) + i(\varphi + 2k\pi)} = e^{a_k}, |
|||
\end{array} |
|||
</math> |
|||
dengan {{math|ln(''r'')}} adalah fungsi logaritma real tunggal, {{math|''a''<sub>''k''</sub>}} menyatakan logaritma kompleks dari {{mvar|z}}, dan {{mvar|k}} bilangan bulat sembarang. Karena itu, logaritma kompleks dari {{mvar|z}}, yang semua bilangan kompleks {{math|''a''<sub>''k''</sub>}} untuk {{mvar|e}} pangkat {{math|''a''<sub>''k''</sub>}} sama dengan {{mvar|z}}, mempunyai tak berhingga banyaknya nilai |
|||
: <math>a_k = \ln (r) + i (\varphi + 2 k \pi),\quad</math> untuk bilangan bulat sembarang {{mvar|k}}. |
|||
[[Berkas:Complex log domain.svg|al=A density plot. In the middle there is a black point, at the negative axis the hue jumps sharply and evolves smoothly otherwise.|jmpl|Cabang prinsip (-{{pi}}, {{pi}}) dari prinsip logaritma kompleks, {{math|Log(''z'')}}. Titik berwarna hitam di {{math|''z'' {{=}} 1}} berpadanan dengan nilai titik nol dan warna yang lebih cerah mengacu pada nilai mutlak lebih besar. [[Rona]] dari warna mengkodekan argumen dari {{math|Log(''z'')}}.|kiri]] |
|||
Dengan mengambil {{mvar|k}} sehingga {{Math|''φ'' + 2''k''{{pi}}}} ada di dalam selang yang ditentukan untuk argumen prinsip, maka {{math|''a''<sub>''k''</sub>}} disebut ''nilai prinsip'' dari logaritma, dinotasikan sebagai {{math|Log(''z'')}}. Argumen prinsip setiap bilangan real positif {{mvar|x}} bernilai 0, jadi {{math|Log(''x'')}} adalah sebuah bilangan real yang sama dengan logaritma (alami). Akan tetapi, rumus logaritma tentang darab dan perpangkatan bilangan di atas [[Eksponensiasi#Kegagalan identitas perpangkatan dan logaritma|tidak memberikan perumuman]] terkait nilai prinsip dari logaritma kompleks.<ref>{{Citation|last1=Wilde|first1=Ivan Francis|title=Lecture notes on complex analysis|publisher=Imperial College Press|location=London|isbn=978-1-86094-642-4|year=2006|url=https://books.google.com/books?id=vrWES2W6vG0C&q=complex+logarithm&pg=PA97}}, teorema 6.1.</ref> |
|||
Ilustrasi tersebut menggambarkan {{math|Log(''z'')}}, membatasi argumen {{mvar|z}} dengan interval {{open-closed|−π, π}}. Cara memadankan cabang dari logaritma kompleks mempunyai ketakkontinuan di sepanjang sumbu-{{mvar|x}} real negatif, seperti yang dapat dilihat pada lompatan hue di gambar. Saat melintasi batas, ketakkontinuan tersebut dimulai dari lompatan hingga batas lain yang ada di cabang yang sama, dalam artian bahwa tiada perubahan dengan nilai-{{mvar|k}} dari cabang tetangga kontinu yang berpadanan. Lokus tersebut dinamakan [[potongan cabang]]. Dengan menghapus perbatasan argumen, maka relasi "argumen dari {{mvar|z}}" dan "logaritma dari {{mvar|z}}" menjadi [[fungsi bernilai banyak]]. |
|||
=== Kebalikan dari fungsi eksponensial lainnya === |
|||
Eksponensiasi muncul dalam cabang matematika dan fungsi inversnya seringkali mengacu pada logaritma. Sebagai contoh, [[logaritma matriks]] merupakan fungsi invers (bernilai banyak) dari [[eksponensial matriks]].<ref>{{Citation|last1=Higham|first1=Nicholas|author1-link=Nicholas Higham|title=Functions of Matrices. Theory and Computation|location=Philadelphia, PA|publisher=[[Society for Industrial and Applied Mathematics|SIAM]]|isbn=978-0-89871-646-7|year=2008}}, bab 11.</ref> Contohnya lain seperti [[Fungsi logaritma p-adic|fungsi logaritma ''p''-adic]], fungsi invers dari [[Fungsi eksponensial p-adic|fungsi eksponensial ''p''-adic]]. Kedua fungsi tersebut didefinisikan melalui deret Taylor yang analog dengan kasus bilangan real.<ref>{{Neukirch ANT|mode=cs2}}, bagian II.5.</ref> Dalam konteks [[geometri diferensial]], [[Peta eksponensial (geometri Riemann)|peta eksponensial]] memetakan [[ruang garis singgung]] di sebuah titik [[Lipatan terdiferensialkan|lipatan]] ke [[lingkungan (matematika)|lingkungan]] titik tersebut. Kebalikannya juga disebut peta logaritma.<ref>{{Citation|last1=Hancock|first1=Edwin R.|last2=Martin|first2=Ralph R.|last3=Sabin|first3=Malcolm A.|title=Mathematics of Surfaces XIII: 13th IMA International Conference York, UK, September 7–9, 2009 Proceedings|url=https://books.google.com/books?id=0cqCy9x7V_QC&pg=PA379|publisher=Springer|year=2009|page=379|isbn=978-3-642-03595-1}}</ref> |
|||
Dalam konteks [[grup hingga]], eksponensiasi dinyatakan dengan mengalikan satu anggota grup {{mvar|b}} dengan dirinya secara berulang. [[Logaritma diskret]] merupakan bilangan bulat ''{{mvar|n}}'' yang menyelesaikan persamaan |
|||
: <math>b^n = x,</math> |
|||
dengan {{mvar|x}} adalah anggota dari grup. Mengerjakan solusi eksponensiasi dapat dilakukan dengan efisien, namun logaritma diskret dipercayai bahwa sangat sulit untuk menghitungnya dalam beberapa grup. Asimetri dari grup tersebut mempunyai penerapan penting dalam [[kriptografi kunci publik]], contohnya seperti [[pertukaran kunci Diffie–Hellman]], sebuah pertukaran kunci sehari-hari yang memungkinkan pertukaran kunci [[kriptografi]] terhadap saluran informasi yang tidak diamankan.<ref>{{Citation|last1=Stinson|first1=Douglas Robert|title=Cryptography: Theory and Practice|publisher=[[CRC Press]]|location=London|edition=3rd|isbn=978-1-58488-508-5|year=2006}}</ref> [[Logaritma Zech]] berkaitan dengan logaritma diskret dalam grup perkalian anggota taknol dari [[medan hingga]].<ref>{{Citation|last1=Lidl|first1=Rudolf|last2=Niederreiter|first2=Harald|author2-link=Harald Niederreiter|title=Finite fields|publisher=Cambridge University Press|isbn=978-0-521-39231-0|year=1997|url-access=registration|url=https://archive.org/details/finitefields0000lidl_a8r3}}</ref> |
|||
{{anchor|double logarithm}}Adapun fungsi invers berupa logaritma lainnya. Fungsi tersebut di antaranya: ''logaritma ganda'' {{math|ln(ln(''x''))}} yang merupakan kebalikan dari [[fungsi eksponensial ganda]], ''[[superlogaritma]]'' yang merupakan kebalikan dari [[tetrasi]], [[fungsi Lambert W]] yang merupakan kebalikan dari fungsi {{math|''f''(''w'') {{=}} ''we<sup>w</sup>''}},<ref>{{Citation|last1=Corless|url=http://www.apmaths.uwo.ca/~djeffrey/Offprints/W-adv-cm.pdf|archive-date=14 Desember 2010|archive-url=https://web.archive.org/web/20101214110615/http://www.apmaths.uwo.ca/~djeffrey/Offprints/W-adv-cm.pdf|access-date=13 Februari 2011|s2cid=29028411|doi=10.1007/BF02124750|pages=329–59|volume=5|issn=1019-7168|journal=Advances in Computational Mathematics|year=1996|title=On the Lambert ''W'' function|first1=R.|author5-link=Donald Knuth|first5=Donald|last5=Knuth|first4=D.|last4=Jeffrey|first3=D.|last3=Hare|first2=G.|last2=Gonnet|url-status=dead}}</ref> dan [[logit]] yang merupakan kebalikan dari [[fungsi logistik]].<ref>{{Citation|last1=Cherkassky|first1=Vladimir|last2=Cherkassky|first2=Vladimir S.|last3=Mulier|first3=Filip|title=Learning from data: concepts, theory, and methods|publisher=[[John Wiley & Sons]]|location=New York|series=Wiley series on adaptive and learning systems for signal processing, communications, and control|isbn=978-0-471-68182-3|year=2007}}, hlm. 357</ref> |
|||
=== Konsep yang berkaitan === |
|||
Berdasarkan sudut pandang [[teori grup]], identitas {{math|log(''cd'') {{=}} log(''c'') + log(''d'')}} menyatakan [[isomorfisme grup]] antara bilangan [[Bilangan riil|riil]] positif terhadap perkalian bilangan riil positif terhadap penambahan. Fungsi logaritmik hanya isomorfisme kontinu antara grup.<ref>{{Citation|last1=Bourbaki|first1=Nicolas|author1-link=Nicolas Bourbaki|title=General topology. Chapters 5–10|publisher=[[Springer-Verlag]]|location=Berlin, New York|series=Elements of Mathematics|isbn=978-3-540-64563-4|mr=1726872|year=1998}}, bagian V.4.1</ref> Berdasarkan pengertian isomorfisme tersebut, [[ukuran Haar]] ([[ukuran Lebesgue]]) {{math|''dx''}} pada riil berpadanan dengan ukuran Haar {{math|{{sfrac|1=''dx''|2=''x''}}}} pada bilangan real positif.<ref>{{Citation|last1=Ambartzumian|first1=R.V.|author-link=Rouben V. Ambartzumian|title=Factorization calculus and geometric probability|publisher=[[Cambridge University Press]]|isbn=978-0-521-34535-4|year=1990|url-access=registration|url=https://archive.org/details/factorizationcal0000amba}}, bagian 1.4</ref> Bilangan riil taknegatif tidak hanya terhadap operasi perkalian, namun juga terhadap operasi penambahan, dan bilangan riil taknegatif membentuk [[semigelanggang]], yang disebut sebagai [[Semigelanggang#Probabilitas semigelanggang|semigelanggang probabilitas]], bahkan membentuk [[semigelanggang]]. Maka logaritma yang mengambil perkalian dengan penambahan (perkalian logaritma), dan mengambil penambahan dengan penambahan logaritma, memberikan [[isomorfisme]] semigelanggang di antara semigelanggang probabilitas dan [[semigelanggang logaritma]]. |
|||
Konsep ini juga terdapat di dalam [[analisis kompleks]] dan [[geometri aljabar]], yang [[Bentuk logaritmik|logaritmik satu bentuk ]]{{math|''df''/''f''}} adalah [[bentuk diferensial]] dengan [[Pole (analisis kompleks)|pole]] logaritmik.<ref>{{Citation|last1=Esnault|first1=Hélène|last2=Viehweg|first2=Eckart|title=Lectures on vanishing theorems|location=Basel, Boston|publisher=Birkhäuser Verlag|series=DMV Seminar|isbn=978-3-7643-2822-1|mr=1193913|year=1992|volume=20|doi=10.1007/978-3-0348-8600-0|citeseerx=10.1.1.178.3227}}, bagian 2</ref> |
|||
Selain itu, terdapat [[polilogaritma]], sebuah fungsi yang didefinisikan sebagai |
|||
: <math> \operatorname{Li}_s(z) = \sum_{k=1}^\infty {z^k \over k^s}. </math> |
|||
Fungsi ini mempunyai kaitan dengan [[logaritma alami]] dengan {{math|1=Li<sub>1</sub> (''z'') = −ln(1 − ''z'')}}. Terlebih lagi, ketika {{math|1=''z'' = 1}}, nilai dari {{math|Li<sub>''s''</sub> (1)}} sama dengan [[fungsi zeta Riemann]], yang dinyatakan sebagai {{math|ζ(''s'')}}.<ref>{{dlmf|id=25.12|first=T.M.|last=Apostol}}</ref> |
|||
== Lihat pula == |
|||
* [[Logaritma umum|Eksponen desimal]] (dex) |
|||
* [[Fungsi eksponensial]] |
|||
* [[Indeks artikel logaritma]] |
|||
* [[Notasi ilmiah#Notasi yang dinormalisasi|Notasi logaritmik]] |
|||
== Catatan == |
|||
{{reflist|30em|group=nb}} |
|||
== Referensi == |
|||
{{Reflist}} |
|||
== Pranala luar == |
|||
* {{Commons category-inline}} |
|||
* {{Wiktionary-inline}} |
|||
*{{sister-inline|project=v|links=[[v:Speak Math Now!/Week 9: Six rules of Exponents/Logarithms|A lesson on logarithms can be found on Wikiversity]]|short=yes}} |
|||
* {{MathWorld|Logarithm|Logarithm|mode=cs2}} |
|||
* [https://web.archive.org/web/20121218200616/http://www.khanacademy.org/math/algebra/logarithms-tutorial Khan Academy: Logarithms, free online micro lectures] |
|||
* {{springer|title=Logarithmic function|id=p/l060600}} |
|||
* {{Citation|author=Colin Byfleet|url=http://mediasite.oddl.fsu.edu/mediasite/Viewer/?peid=003298f9a02f468c8351c50488d6c479|title=Educational video on logarithms|access-date=12 October 2010}} |
|||
* {{Citation|author=Edward Wright|url=http://www.johnnapier.com/table_of_logarithms_001.htm|title=Translation of Napier's work on logarithms|access-date=12 October 2010|url-status=unfit|archive-url=https://web.archive.org/web/20021203005508/http://www.johnnapier.com/table_of_logarithms_001.htm|archive-date=3 December 2002}} |
|||
* {{Cite EB1911|wstitle=Logarithm|volume=16|pages=868–77|first=James Whitbread Lee|last=Glaisher|mode=cs2}} |
|||
{{Daftar fungsi matematika}}{{Authority control}} |
|||
[[Kategori:Matematika]] |
|||
[[Kategori:Persamaan diferensial]] |
|||
[[Kategori:Persamaan matematika]] |
|||
[[Kategori:Persamaan]] |
|||
Revisi terkini sejak 22 April 2024 02.06

| Operasi aritmetika | ||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
Dalam matematika, logaritma adalah fungsi invers dari eksponensiasi. Dengan kata lain, logaritma dari x adalah eksponen dengan bilangan pokok b yang dipangkatkan dengan bilangan konstan lain agar memperoleh nilai x. Kasus sederhana dalam logaritma adalah menghitung jumlah munculnya faktor yang sama dalam perkalian berulang. Sebagai contoh, 1000 = 10 × 10 × 10 = 103 dibaca, "logaritma 1000 dengan bilangan pokok 10 sama dengan 3" atau dinotasikan sebagai 10log (1000) = 3. Logaritma dari x dengan bilangan pokok b dilambangkan blog x. Terkadang logaritma dilambangkan sebagai logb (x) atau tanpa menggunakan tanda kurung, logb x, atau bahkan tanpa menggunakan bilangan pokok khusus, log x.
Ada tiga bilangan pokok logaritma yang umum beserta kegunaannya. Logaritma dengan bilangan pokok 10 (b = 10) disebut sebagai logaritma umum, yang biasanya dipakai dalam ilmu sains dan rekayasa. Logaritma dengan dengan bilangan pokok bilangan e (b ≈ 2.718) disebut sebagai logaritma alami, yang dipakai dengan luas dalam matematika dan fisika, karena dapat mempermudah perhitungan integral dan turunan. Logaritma dengan bilangan pokok 2 (b = 2) disebut sebagai logaritma biner, yang seringkali dipakai dalam ilmu komputer.
Logaritma diperkenalkan oleh John Napier pada tahun 1614 sebagai alat yang menyederhanakan perhitungan.[1] Logaritma dipakai lebih cepat dalam navigator, ilmu sains, rekayasa, ilmu ukur wilayah, dan bidang lainnya untuk lebih mempermudah perhitungan nilai yang sangat akurat. Dengan menggunakan tabel logaritma, cara yang membosankan seperti mengalikan digit yang banyak dapat digantikan dengan melihat tabel dan penjumlahan yang lebih mudah. Ini dapat dilakukan karena logaritma dari hasil kali bilangan merupakan logaritma dari jumlah faktor bilangan:
asalkan bahwa b, x dan y bilangan positif dan b ≠ 1. Mistar hitung yang juga berasal dari logaritma dapat mempermudah perhitungan tanpa menggunakan tabel, namun perhitungannya kurang akurat. Leonhard Euler mengaitkan gagasan logaritma saat ini dengan fungsi eksponensial pada abad ke-18, dan juga memperkenalkan huruf e sebagai bilangan pokok dari logaritma alami.[2]
Penerapan skala logaritmik dipakai dalam mengurangi kuantitas yang sangat besar menjadi lebih kecil. Sebagai contoh, desibel (dB) adalah satuan yang digunakan untuk menyatakan rasio sebagai logaritma, sebagian besar untuk kekuatan sinyal dan amplitudo (contoh umumnya pada tekanan suara). Dalam kimia, pH mengukur keasaman dari larutan berair melalui logaritma. Logaritma umumnya dipakai dalam rumus ilmiah, dalam pengukuran kompleksitas algoritma dan objek geometris yang disebut sebagai fraktal. Logaritma juga membantu untuk menjelaskan frekuensi rasio interval musik, ditemukan di rumus yang menghitung bilangan prima atau hampiran faktorial, memberikan gambaran dalam psikofisika, dan dapat membantu perhitungan akuntansi forensik.
Konsep logaritma sebagai invers dari eksponensiasi juga memperluas ke struktur matematika lain. Namun pada umumnya, logaritma cenderung merupakan fungsi bernilai banyak. Sebagai contoh, logaritma kompleks merupakan invers dari fungsi eksponensial pada bilangan kompleks. Mirip dengan contoh sebelumnya, logaritma diskret dalam grup hingga, merupakan invers fungsi eksponensial bernilai banyak yang memiliki kegunaan dalam kriptografi kunci publik.
Alasan
[sunting | sunting sumber]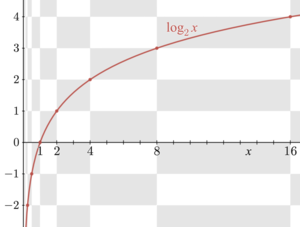
Operasi aritmetika yang paling dasar adalah penambahan, perkalian, dan eksponen. Kebalikan dari penambahan adalah pengurangan, dan kebalikan dari perkalian adalah pembagian. Mirip dengan contoh sebelumnya, logaritma merupakan kebalikan (atau invers) dari operasi eksponensiasi. Eksponensiasi adalah bilangan bilangan pokok b yang ketika dipangkatkan dengan y memberikan nilai x. Ini dirumuskan sebagai
Sebagai contoh, 2 pangkat 3 memberikan nilai 8. Secara matematis, .
Logaritma dengan bilangan pokok b adalah operasi invers yang menyediakan nilai keluaran y dari nilai masukan x. Hal ini mengartikan bahwa y = blog x ekuivalen dengan x = by, jika b bilangan real positif. (Jika b bukanlah bilangan real positif, eksponensiasi dan logaritma dapat terdefinisi tetapi membutuhkan beberapa nilai, sehingga definisi darinya semakin rumit.)
Salah satu alasan bersejarah utamanya dalam memperkenalkan logaritma adalah rumus
yang dapat mempermudah perhitungan nilai perkalian dan pembagian dengan penjumlahan, pengurangan, dan melihat tabel logaritma. Perhitungan ini dipakai sebelum komputer ditemukan.
Definisi
[sunting | sunting sumber]Diberikan bilangan real positif b sehingga b ≠ 1, maka logaritma dari bilangan real positif x terhadap bilangan pokok b[nb 1] adalah eksponen dengan bilangan pokok b yang dipangkatkan bilangan agar memperoleh nilai x. Dengan kata lain, logaritma bilangan pokok b dari x adalah bilangan real y sehingga by = x.[3] Logaritma dilambangkan sebagai blog x (dibaca "logaritma x dengan bilangan pokok b"). Terdapat definisi yang mirip dan lebih ringkas mengatakan bahwa fungsi blog invers dengan fungsi x ↦ bx.
Sebagai contoh, 2log 16 = 4, karena 24 = 2 × 2 × 2 × 2 = 16. Logaritma juga dapat bernilai negatif, contohnya 2log 12 = –1, karena 2–1 = 121 = 12. Logaritma juga berupa nilai desimal, sebagai contoh 10log 150 kira-kira sama dengan 2,176 karena terletak di antara 2 dan 3, dan begitupula 150 terletak antara 102 = 100 dan 103 = 1000. Adapun sifat logaritma bahwa untuk setiap b, blog b = 1 karena b1 = b, dan blog 1 = 0 karena b0 = 1.
Identitas logaritma
[sunting | sunting sumber]Ada beberapa rumus penting yang mengaitkan logaritma dengan yang lainnya.[4]
Hasil kali, hasil bagi, pangkat, dan akar
[sunting | sunting sumber]Logaritma dari hasil kali merupakan jumlah logaritma dari bilangan yang dikalikan, dan logaritma dari hasil bagi dari dua bilangan merupakan selisih logaritma. Logaritma dari bilangan pangkat ke-p sama dengan p dikali logaritma dari bilangan tersendiri, dan logaritma bilangan akar ke-p sama dengan logaritma dibagi dengan p. Tabel berikut memuat daftar sifat-sifat logaritma tersebut beserta contohnya. Masing-masing identitas ini diperoleh dari hasil substitusi dari definisi logaritma atau pada ruas kiri persamaan.
| Rumus | Contoh | |
|---|---|---|
| Hasil kali | ||
| Hasil bagi | ||
| Pangkat | ||
| Akar |
Mengubah bilangan pokok
[sunting | sunting sumber]Logaritma blog x dapat dihitung sebagai hasil bagi logaritma x dengan logaritma b terhadap bilangan pokok sembarang k. Secara matematis dirumuskan sebagai:
| Bukti konversi antara logaritma dari bilangan pokok sembarang |
|---|
|
Dimulai dari identitas berikut ini dapat menerapkan klog pada kedua ruas sehingga memperoleh
Ketika mencari penyelesaian untuk blog x, maka menghasilkan persamaan:
Hal ini memperlihatkan faktor konversi dari nilai klog ke nilai blog yang serupa agar memperoleh bentuk 1klog b |
Kalkulator ilmiah merupakan alat yang menghitung logaritma dengan bilangan pokok 10 dan e.[5] Logaritma terhadap setiap bilangan pokok b dapat ditentukan menggunakan kedua logaritma tersebut melalui rumus sebelumnya:
Diberikan suatu bilangan x dan logaritma y = blog x, dengan b adalah bilangan pokok yang tidak diketahui. Bilangan pokok tersebut dapat dinyatakan dengan
Rumus ini dapat diperlihatkan dengan mengambil persamaan yang mendefinisikan x = bblog x = by, lalu dipangkatkan dengan 1y.
Bilangan pokok khusus
[sunting | sunting sumber]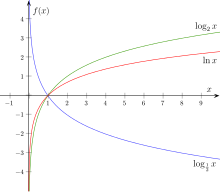
Secara khusus, terdapat tiga bilangan pokok yang umum di antara semua pilihan bilangan pokok pada logaritma. Ketiga bilangan pokok tersebut adalah b = 10, b = e (konstanta bilangan irasional yang kira-kira sama dengan 2,71828), dan b = 2 (logaritma biner). Dalam analisis matematika, logaritma dengan bilangan pokok e tersebar karena sifat analitik yang dijelaskan di bawah. Di sisi lain, logaritma dengan bilangan pokok 10 mudah dipakai dalam perhitungan manual dalam sistem bilangan desimal:[6]
Jadi, 10log x berkaitan dengan jumlah digit desimal dari bilangan bulat positif x: jumlah digitnya merupakan bilangan bulat terkecil yang lebih besar dari 10log x.[7] Sebagai contoh, 10log 1430 kira-kira sama dengan 3,15. Bilangan berikutnya merupakan jumlah digit dari 1430, yaitu 4. Dalam teori informasi, logaritma alami dipakai dalam nat dan logaritma dengan bilangan pokok 2 dipakai dalam bit sebagai satuan dasar informasi.[8] Logaritma biner juga dipakai dalam ilmu komputer, dengan sistem biner ditemukan dimana-mana. Dalam teori musik, rasio tinggi nada kedua (yaitu oktaf) ditemukan dimana-mana dan jumlah sen antara setiap dua tinggi nada dirumuskan sebagai konstanta 1200 dikali logaritma dari rasio (yaitu, 100 sen per setengah nada dengan temperamen sama). Dalam fotografi, logaritma dengan bilangan pokok dua dipakai untuk mengukur nilai pajanan, tingkatan cahaya, waktu eksposur, tingkap, dan kecepatan film dalam "stop".[9]
Tabel berikut memuat notasi-notasi umum mengenai bilangan pokok beserta bidang yang dipakai. Selain blog x, adapula notasi logaritma lain yang ditulis sebagai logb x, dan juga seperti log x. Pada kolom "Notasi ISO" memuat penamaan yang disarankan Organisasi Standardisasi Internasional, yakni ISO 80000-2.[10] Karena notasi log x telah dipakai untuk ketiga bilangan pokok di atas (atau ketika bilangan pokok belum ditentukan), bilangan pokok yang dimaksud harus sering diduga tergantung konteks atau bidangnya. Sebagai contoh, log biasanya mengacu pada 2log dalam ilmu komputer, dan log mengacu pada elog.[11] Dalam konteks lainnya, log seringkali mengacu pada 10log.[12]
| Bilangan pokok
b |
Nama blog x | Notasi ISO | Notasi lain | Dipakai dalam bidang |
|---|---|---|---|---|
| 2 | logaritma biner | lb x[13] | ld x, log x, lg x,[14] 2log x | ilmu komputer, teori informasi, bioinformatika, teori musik, fotografi |
| e | logaritma alami | ln x[nb 2] | log x (dipakai dalam matematika[18] dan beberapa bahasa pemrograman lainnya[nb 3]), elog x | matematika, fisika, kimia, |
| 10 | logaritma biasa | lg x | log x, 10log x
(dipakai dalam rekayasa, biologi, dan astronomi) |
bidang berbagai rekayasa (lihat desibel dan lihat di bawah),
tabel logaritma, kalkulator genggam, spektroskopi |
| b | logaritma dengan bilangan pokok b | blog x | matematika |
Sejarah
[sunting | sunting sumber]Sejarah logaritma yang dimulai dari Eropa pada abad ketujuh belas merupakan penemuan fungsi terbaru yang memperluas dunia analisis di luar keterbatasan metode aljabar. Metode logaritma dikemukakan secara terbuka oleh John Napier pada tahun 1614, dalam bukunya yang berjudul Mirifici Logarithmorum Canonis Descriptio.[19][20] Namun, teknik-teknik lain sebelum penemuan Napier sudah ada dengan keterbatasan metode yang serupa, contohnya seperti prosthafaeresis atau penggunaan tabel barisan, yang dikembangkan dengan luas oleh Jost Bürgi sekitar tahun 1600.[21][22] Napier menciptakan istilah untuk logaritma dalam bahasa Latin Tengah, “logaritmus”, yang berasal dari gabungan dua kata Yunani, logos “proporsi, rasio, kata” + arithmos “bilangan”. Secara harfiah, "logaritmus" berarti “bilangan rasio”.
Logaritma umum dari bilangan adalah indeks dari perpangkatan sepuluh yang sama dengan bilangan tersebut.[23] Bilangan yang sangat membutuhkan banyak angka merupakan kiasan kasar untuk logaritma umum, dan Archimedes menyebutnya sebagai “orde bilangan”.[24] Logaritma real pertama adalah metode heuristik yang mengubah perkalian menjadi penjumlahan, sehingga memudahkan perhitungan yang cepat. Ada beberapa metode yang menggunakan tabel yang diperoleh dari identitas trigonometri,[25] dan metode tersebut dinamakan prosthafaeresis.
Penemuan fungsi yang dikenal saat ini sebagai logaritma alami, berawal dari saat Grégoire de Saint-Vincent mencoba menggambarkan kuadratur hiperbola persegi panjang. Archimedes menulis risalah yang berjudul The Quadrature of the Parabola pada abad ke-3 SM, tetapi kuadratur hiperbola menghindari semua upayanya hingga Saint-Vincent menerbitkan hasilnya pada tahun 1647. Logaritma yang mengaitkan barisan dan deret geometri dalam argumen dan nilai barisan dan deret aritmetika, meminta Antonio de Sarasa untuk mengaitkan kuadratur Saint-Vincent dan tradisi logaritma dalam prosthafaeresis sehingga mengarah ke sebuah persamaan kata untuk logaritma alami, yaitu "logaritma hiperbolik". Christiaan Huygens dan James Gregory mulai mengenali fungsi baru tersebut. Leibniz memakai notasi Log y pada tahun 1675,[26] dan tahun berikutnya ia mengaitkannya dengan integral
Sebelum Euler mengembangkan konsep modernnya tentang logaritma alami kompleks, Roger Cotes memperlihatkan hasil yang hampir sama pada tahun 1714 bahwa[27]
- .
Tabel logaritma, mistar hitung, dan penerapan bersejarah
[sunting | sunting sumber]
Dengan menyederhanakan perhitungan yang rumit sebelum adanya mesin hitung komputer, logaritma berkontribusi pada kemajuan pengetahuan, khususnya astronomi. Logaritma sangat penting terhadap kemajuan dalam survei, navigasi benda langit, dan cabang lainnya. Pierre-Simon Laplace menyebut logaritma sebagai
- "...kecerdasan yang mengagumkan, [sebuah alat] yang mengurangi pekerjaan berbulan-bulan menjadi beberapa hari, menggandakan kehidupan astronom, dan menghindarinya dari kesalahan dan rasa jijik yang tak terpisahkan dari perhitungan yang panjang."[28]
Karena fungsi f(x) = bx adalah fungsi invers dari blog x, maka fungsi tersebut disebut sebagai antilogaritma.[29] Saat ini, antilogaritma lebih sering disebut fungsi eksponensial.
Tabel logaritma
[sunting | sunting sumber]Sebuah alat penting yang memungkinkan penggunaan logaritma adalah tabel logaritma.[30] Tabel logaritma pertama kali disusun oleh Henry Briggs pada tahun 1617 setelah penemuan Napier, tetapi penemuannya menggunakan 10 sebagai bilangan pokok. Tabel pertamanya memuat logaritma umum dari semua bilangan bulat yang berkisar antara 1 dengan 1000, dengan ketepatan yang dimiliki 14 digit, dan kemudian ia membuat tabel dengan kisaran yang besar. Tabel tersebut mencantumkan nilai untuk setiap bilangan dalam kisaran dan ketepatan tertentu. Karena bilangan yang berbeda dengan faktor 10 memiliki logaritma yang berbeda dengan bilangan bulat, logaritma dengan bilangan pokok 10 digunakan secara universal untuk perhitungan, sehingga disebut logaritma umum. Logaritma umum dari dipisahkan menjadi bagian bilangan bulat yang dikenal sebagai karakteristik, dan bagian pecahan (bahasa Inggris: fractional part) yang dikenal sebagai mantissa. Tabel logaritma hanya perlu menyertakan mantissa, karena karakteristik logaritma umum dapat dengan mudah ditentukan dengan menghitung angka dari titik desimal.[31] Karakteristik logaritma umum dari sama dengan satu ditambah karakteristik , dan mantissanya sama. Dengan menggunakan tabel logartima dengan tiga digit, nilai logaritma dari 3542 kira-kira sama dengan
Nilainya dengan ketepatan yang sangat tinggi dapat diperoleh melalui interpolasi:
Nilai dapat ditentukan dengan pencarian terbalik pada tabel yang sama, karena logaritma merupakan fungsi monoton.
Perhitungan
[sunting | sunting sumber]Hasil kali atau hasil bagi dari dua bilangan positif c dan d biasanya dihitung sebagai penambahan dan pengurangan logaritma. Hasil kali cd berasal dari antilogaritma dari penambahan dan hasil bagi cd berasal dari antilogaritma dari pengurangan, melalui tabel yang sama:
dan
Untuk perhitungan manual yang meminta ketelitian yang cukup besar, melakukan pencarian kedua logaritma, menghitung jumlah atau selisihnya, dan mencari antilogaritma jauh lebih cepat daripada menghitung perkalian dengan metode sebelumnya seperti prosthafaeresis, yang mengandalkan identitas trigonometri.
Perhitungan pangkat direduksi menjadi perkalian, dan sedangkan perhitungan akar direduksi menjadi pembagian. Pernyataan ini dapat dilihat sebagai
dan
Perhitungan trigonometri dilengkapi dengan tabel-tabel yang memuat logaritma umum dari fungsi trigonometri.
Mistar hitung
[sunting | sunting sumber]Penerapan penting lainnya adalah mistar hitung, sepasang skala yang dibagi secara logaritmik yang digunakan dalam perhitungan. Adapun skala logaritmik yang tidak memiliki sorong, mistar Gunter, ditemukan tak lama setelah penemuan Napier dan disempurnakan oleh William Oughtred untuk menciptakan sepasang skala logaritmik yang dapat dipindahkan terhadap satu sama lain, yaitu mistar hitung. Angka yang ditempatkan pada skala hitung pada jarak sebanding dengan selisih antara logaritmanya. Menggeser skala atas dengan tepat berarti menambahkan logaritma secara mekanis, seperti yang diilustrasikan berikut ini:

Sebagai contoh, dengan menambahkan jarak dari 1 ke 2 pada skala di bagian bawah ke jarak dari 1 ke 3 pada skala di bagian atas menghasilkan hasil kali 6, yang dibacakan di bagian bawah. Mistar hitung adalah sebuah alat menghitung yang penting bagi para insinyur dan ilmuwan hingga tahun 1970-an, karena dengan mengorbankan ketepatan nilai memungkinkan perhitungan yang jauh lebih cepat daripada teknik berdasarkan tabel.[32]
Sifat analitik
[sunting | sunting sumber]Kajian yang lebih dalam mengenai logaritma memerlukan sebuah konsep yang disebut fungsi. Fungsi merupakan sebuah kaidah yang dipetakan suatu bilangan akan menghasilkan bilangan lain.[33] Contohnya seperti fungsi yang menghasilkan bilangan konstan b, yang dipangkatkan setiap bilangan real x. Fungsi ini secara matematis ditulis sebagai f(x) = b x. Ketika b positif dan tak sama dengan 1, maka f adalah fungsi terbalikkan ketika dianggap sebagai fungsi dengan interval dari bilangan real ke bilangan real positif.
Keberadaan
[sunting | sunting sumber]Misalkan b adalah bilangan real positif yang tidak sama dengan 1 dan misalkan f(x) = b x. Pernyataan yang diikuti dari teorema nilai antara ini,[34] merupakan hasil standar dalam analisis real yang mengatakan bahwa setiap fungsi monoton sempurna dan kontinu merupakan fungsi bijektif antara ranah (bahasa Inggris: domain) dan kisarannya (bahasa Inggris: range). Pernyataan saat ini mengatakan bahwa f yang menaik sempurna (untuk b > 1), atau menurun sempurna (untuk 0 < b < 1)[35] merupakan fungsi kontinu, memiliki ranah dan memiliki kisaran . Oleh karena itu, f adalah fungsi bijeksi dari ke . Dengan kata lain, untuk setiap bilangan real positif y, terdapat setidaknya satu bilangan real x sehingga .
Misalkan yang menyatakan invers dari fungsi f. Dalam artian, blog y adalah bilangan real tunggal x sehingga . Fungsi ini disebut fungsi logaritma dengan bilangan pokok-b atau fungsi logaritmik (atau logaritma saja).
Karakterisasi melalui rumus hasil kali
[sunting | sunting sumber]Pada dasarnya, fungsi blog x juga dapat dikarakterisasikan melalui rumus hasil kali
Lebih tepatnya, logaritma untuk setiap bilangan pokok b > 1 yang hanya merupakan fungsi f naik dari bilangan real positif ke bilangan real memenuhi sifat bahwa f(b) = 1 dan[36]
Grafik fungsi logaritma
[sunting | sunting sumber]
Seperti yang dibahas sebelumnya, fungsi blog invers terhadap fungsi eksponensial . Karena itu, grafiknya berkorespondensi dengan satu sama lain saat menukar koordinat-x dan koordinat-y (atau saat melakukan pencerminan di garis diagonal x = y), seperti yang diperlihatkan sebagai berikut: sebuah titik (t, u = bt) pada grafik dari f menghasilkan sebuah titik (u, t = blog u) pada grafik logaritma dan sebaliknya. Akibatnya, blog (x) divergen menuju takhingga (dalam artian semakin besar dari setiap bilangan yang diberikan) jika x naik menuju takhingga, asalkan b lebih besar dari satu. Pada kasus tersebut, blog(x) merupakan fungsi menaik. Sedangkan untuk kasus b < 1, blog (x) cenderung menuju ke negatif takhingga. Ketika x mendekati nol, blog x menuju ke negatif takhingga untuk b > 1 dan menuju ke plus takhingga untuk b < 1.
Turunan dan antiturunan
[sunting | sunting sumber]
Sifat analitik tentang fungsi adalah melalui fungsi inversnya.[34] Jadi, ketika f(x) = bx adalah fungsi kontinu dan terdiferensialkan, maka blog y fungsi kontinu dan terdiferensialkan juga. Penjelasan kasarnya, sebuah fungsi kontinu adalah terdiferensialkan jika grafiknya tidak mempunyai "ujung" yang tajam. Lebih lanjut, ketika turunan dari f(x) menghitung nilai ln(b) bx melalui sifat-sifat fungsi eksponensial, aturan rantai menyiratkan bahwa turunan dari blog x dirumuskan sebagai [35][37]
Artinya, kemiringan dari garis singgung yang menyinggung grafik logaritma dengan bilangan pokok b di titik (x, blog (x)) sama dengan 1x ln(b).
Turunan dari ln(x) adalah 1x, yang berarti ini menyiratkan bahwa ln(x) adalah integral tunggal dari 1x yang mempunyai nilai 0 untuk x = 1. Hal ini merupakan rumus paling sederhana yang mendorong sifat "alami" pada logaritma alami, dan hal ini juga merupakan salah satu alasan pentingnya konstanta e.
Turunan dengan argumen fungsional rampat f(x) dirumuskan sebagai
Hasil bagi pada ruas kanan disebut turunan logaritmik dari f dan menghitung f'(x) melalui turunan dari ln(f(x)) dikenal sebagai pendiferensialan logaritmik.[38] Antiturunan dari logaritma alami ln(x) dirumuskan sebagai:[39]
Terdapat rumus yang berkaitan, seperti antiturunan dari logaritma dengan bilangan pokok lainnya dapat diperoleh dari persamaan ini dengan mengubah bilangan pokoknya.[40]
Representasi integral mengenai fungsi logaritma
[sunting | sunting sumber]
Logaritma alami dari t dapat didefinisikan sebagai integral tentu:
Definisi ini menguntungkan karena tidak bergantung pada fungsi eksponensial atau fungsi trigonometri apapun, dan definisi ini merupakan sebuah integral dari fungsi timbal balik sederhana. Penjelasan dalam integral, ln(t) sama dengan luas antara sumbu-x dan grafik fungsi 1x, yang berkisar dari x = 1 ke x = t. Penjelasan ini juga merupakan akibat dari teorema dasar kalkulus, dan bahkan turunan dari ln(x) sama dengan 1x. Rumus logaritma hasil kali dan pangkat dapat diperoleh melalui definisi ini.[41] Sebagai contoh, rumus hasil kali ln(tu) = ln(t) + ln(u) dapat disimpulkan sebagai:
Persamaan (1) membagi integral menjadi dua bagian, sementara (2) mengubah variabel w menjadi xt. Pada ilustrasi dibawah, pembagian integral tersebut dapat disamakan dengan pembagian luasnya menjadi bagian berwarna kuning dan biru. Dengan mengukur luas berwarna biru kembali secara vertikal melalui faktor t dan menyusutnya melalui faktor yang sama secara horizontal tidak mengubah ukuran luasnya. Dengan memindahkan daerah biru ke daerah kuning, luasnya menyesuaikan grafik fungsi f(x) = 1x lagi. Oleh karena itu, luas biru di sebelah kiri, yang merupakan integral dari fungsi f(x) dengan interval dari t hingga tu sama dengan integral dari fungsi yang sama dengan interval 1 hingga u. Hal ini membenarkan persamaan (2) melalui bukti geometri lainnya.

Rumus pangkat ln(tr) = r ln(t) dapat real dalam cara yang serupa:
Persamaan kedua menggunakan perubahan variabel w = x1r melalui integral substitusi.
Jumlah keseluruhan timbal balik dari bilangan asli yang dirumuskan
disebut deret harmonik. Deret ini sangat terkait erat dengan logaritma alami, yang dinyatakan melalui pernyataan berikut: ketika n cenderung menuju takhingga, selisih dari
konvergen (yakni mendekati dengan sembarang) ke sebuah bilangan yang dikenal sebagai konstanta Euler–Mascheroni γ = 0,5772.... Kaitan antara deret harmonik dan logaritma natural membantu dalam menganalisis kinerja algoritma seperti quicksort.[42]
Transendensi logaritma
[sunting | sunting sumber]Bilangan real yang bukan merupakan bilangan aljabar disebut bilangan transendental[43]. Sebagai contoh, π dan e adalah bilangan transendental, sedangkan bukan. Hampir semua bilangan real adalah transendental. Logaritma merupakan sebuah contoh fungsi transendental. Teorema Gelfond–Schneider mengatakan bahwa logaritma biasanya memberikan nilai transendental.[44]
Perhitungan
[sunting | sunting sumber]
Logaritma merupakan alat hitung yang mudah pada beberapa kasus, seperti 10log 1000 = 3. Logaritma pada umumnya dapat dihitung melalui deret kuasa atau rata-rata aritmetika–geometrik, atau didapatkan kembali dari tabel logaritma (sebelum adanya perhitungan logaritma) yang menyediakan ketepatan nilai konstan.[45][46] Metode Newton, sebuah metode berulang yang menyelesaikan persamaan melalui hampiran, juga dapat dipakai untuk menghitung logaritma, karena fungsi inversnya (yaitu fungsi eksponensial), dapat dihitung dengan cepat.[47] Dengan melihat tabel logaritma, metode yang mirip dengan CORDIC dapat dipakai untuk menghitung logaritma hanya dengan menggunakan operasi penambahan dan geseran bit.[48][49] Terlebih lagi, algoritma dari logaritma biner menghitung lb(x) secara berulang berdasarkan penguadratan x yang berulang dan menggunakan ekspresi
Deret pangkat
[sunting | sunting sumber]Deret Taylor
[sunting | sunting sumber]
Untuk setiap bilangan z yang memenuhi sifat 0 < z ≤ 2, maka berlaku rumus:[nb 4][50]
Pernyataan di atas merupakan tulisan singkat untuk mengatakan bahwa ln(z) dapat diaproksimasi sebagai bilangan yang lebih-lebih akurat lagi melalui ekspresi berikut:
Sebagai contoh, pendekatan ketiga saat z = 1,5 memberikan nilai 0,4167. Nilai tersebut kira-kira 0,011 lebih besar dari ln(1,5) = 0,405465. Deret ini yang mengaproksimasi ln(z) dengan ketepatan nilai sembarang, menyediakan jumlah dari nilai yang dijumlahkan cukup besar. Dalam kalkulus elementer, ln(z) adalah limit dari deret ini dan juga merupakan deret Taylor dari logaritma alami di z = 1. Deret Taylor dari ln(z) khususnya menyediakan alat yang berguna untuk mengaproksimasi ln(1 + z) ketika z bernilai kecil, |z| < 1:
Sebagai contoh, hampiran orde pertama memberikan nilai hampiran ln(1,1) ≈ 0,1 ketika z = 0,1, yang galatnya 5% lebih kecil dari nilai eksak 0,0953.
Deret lebih efisien
[sunting | sunting sumber]Deret lainnya berasal dari fungsi tangen hiperbolik invers:
untuk setiap bilangan real z > 0.[nb 5][50] Dengan menggunakan notasi Sigma, ruas kanan pada rumus di atas juga dapat ditulis sebagai
Deret ini dapat diturunkan dari deret Taylor di atas, yang konvergen lebih cepat daripada deret Taylor, khususnya jika z mendekati 1. Sebagai contoh, untuk z = 1,5, tiga suku pertama dari deret kedua memberikan nilai hampiran ln(1,5) dengan galatnya sekitar 3×10−6. Kekonvergenan cepat untuk z yang mendekati 1 dapat dimanfaatkan sebagai berikut: diberikan sebuah hampiran dengan tingkat akurat yang rendah y ≈ ln(z) dan memasukkan ke rumus
maka logaritma dari z dirumuskan:
Hampiran awalan y yang lebih baik adalah dengan membuat nilai A mendekati ke 1, sehingga nilai logaritma dapat dihitung lebih efisien. Nilai A dapat dihitung melalui deret eksponensial sehingga nilainya konvergen dengan cepat, asalkan nilai y tidak terlalu besar. Dengan menghitung logaritma dari z yang lebih besar dapat direduksi menjadi nilai z yang lebih kecil dengan menulis z = a · 10b, sehingga ln(z) = ln(a) + b · ln(10).
Terdapat metode yang sangat berkaitan dengannya dapat dipakai untuk menghitung logaritma dari bilangan bulat. Dengan memasukkan pada deret di atas, maka deret tersebut dapat ditulis sebagai berikut:
Jika diketahui logaritma dari suatu bilangan bulat n yang lebih besar, maka deret tersebut menghasilkan sebauah deret yang konvergen dengan cepat untuk log(n+1), dengan laju konvergensi dari .
Hampiran purata aritmetika-geometrik
[sunting | sunting sumber]Purata aritmetika–geometrik atau rata-rata aritmetika–geometrik menghasilkan hampiran dari logaritma natural dengan tingkatan ketepatan yang tinggi. Pada tahun 1982, Sasaki dan Kanada memperlihatkan bahwa purata ini sangat cepat untuk ketepatan di antara 400 dan 1000 letak desimal, sementara metode deret Taylor biasanya lebih cepat ketika membutuhkan nilai yang kurang akurat. Dalam karyanya, ln(x) kira-kira sama dengan ketepatan dari 2−p (atau p bit yang tepat) melalui rumus berikut (karena Carl Friedrich Gauss):[51][52]
Notasi M(x, y) menyatakan rata-rata aritmetika–geometrik dari x dan y. Purata ini didapatkan dengan menghitung rerata (x + y)/2 (purata aritmetika) dan (purata geometrik) dari x dan y secara berulang, lalu misalkan kedua bilangan tersebut merupakan bilangan x dan y selanjutnya. Kedua bilangan tersebut konvergen dengan cepat menuju ke limit yang sama, yaitu M(x, y). Agar pasti bahwa nilai yang diperlukan tepat, maka pilih m sehingga
Bilangan m yang lebih besar membuat perhitungan M(x, y), dengan nilai awal x dan y yang merupakan nilai yang sangat jauh, mengambil langkah lebih lanjut agar nilainya konvergen, tetapi memberikan nilai yang lebih tepat. Konstanta seperti π dan ln(2) dapat dihitung melalui deret yang konvergen dengan cepat.
Algoritma Feynman
[sunting | sunting sumber]Richard Feynman, yang mengerjakan proyek Manhattan di Los Alamos National Laboratory, mengembangkan sebuah algoritma pengolahan bit untuk menghitung nilai logaritma. Algoritma tersebut menyerupai pembagian panjang, dan kemudian dipakai dalam sebuah anggota dari rangkaian subkomputer, Connection Machine. Bahkan bahwa setiap bilangan real 1 < x < 2 yang dapat direpresentasikan sebagai hasil kali dari faktor yang berbeda dari bentuk 1 + 2−k, dipakai dalam algoritma ini. Algoritma ini dibangun secara berurutan bahwa hasil kali P, yang dimulai dengan P = 1 dan k = 1, mengatakan bahwa jika P · (1 + 2−k) < x, maka P berubah menjadi P · (1 + 2−k), sehingga membuat nilai menaik. Algoritma tersebut berhenti ketika k cukup besar memberikan nilai akurat yang diinginkan. Karena log(x) adalah jumlah dari suku berbentuk log(1 + 2−k) yang berpadanan dengan nilai k dan faktor 1 + 2−k adalah hasil kali dari P, maka log(x) dapat dihitung melalui operasi penambahan yang sederhana, yaitu menggunakan tabel dari log(1 + 2−k) untuk semua k. Setiap bilangan pokok dapat dipakai untuk tabel logaritma.[53]
Penerapan
[sunting | sunting sumber]
Logaritma memiliki banyak penerapan di dalam maupun di luar matematika. Ada beberapa kejadian penerapan logaritma yang berkaitan dengan gagasan kekararan skala. Sebagai contoh, setiap ruangan yang terdapat di dalam sebuah cangkang nautilus memiliki kira-kira sama dengan jumlah salinan dari ruang selanjutnya, yang ditimbang melalui faktor konstanta. Contoh tersebut menyerupai bentuk spiral logaritmik.[54] Hukum Benford mengenai distribusi dari angka yang ditunjuk juga dapat dijelaskan melalui kekeraran skala.[55] Logaritma juga berkaitan dengan benda yang memiliki kemiripan terhadap diri sendiri. Sebagai contoh, logaritma muncul dalam analisis tentang algoritma yang menyelesaikan masalah dengan membaginya menjadi dua masalah lebih kecil yang serupa dan memotong kecil penyelesaiannya.[56] Dimensi dari bentuk geometrik menyerupai diri sendiri, dalam artian bahwa bentuk yang bagiannya menyerupai gambarnya secara keseluruhan juga dirumuskan melalui logaritma. Skala logaritmik berguna untuk mengukur perubahan relatif nilai daripada selisih mutlaknya. Terlebih lagi, karena fungsi logaritmik log(x) menaik sangat lambat untuk nilai besarx, skala logaritmik biasanya menekan data ilmiah yang berskala besar. Logaritma juga muncul dalam rumus ilmiah numerik, seperti persamaan roket Tsiolkovsky, persamaan Fenske, atau persamaan Nernst.
Penerapannya dalam skala logaritmik
[sunting | sunting sumber]
Satuan kuantitas dalam ilmiah seringkali dinyatakan sebagai logaritma dari kuantitas lain, dengan menggunakan skala logaritmik. Sebagai contoh, desibel merupakan satuan pengukuran yang dikaitkan dengan perhitungan dari kuantitas skala logaritmik. Penguat desibel memberikan 10 kalinya logaritma biasa dari rasio daya atau 20 kalinya logaritma biasa dari rasio tegangan. Satuan inilah yang dipakai untuk mengukur rugi tingkatan ketegangan saat mentransmisi sinyal elektrik,[57] yang bertujuan untuk menjelaskan tingkatan kekuatan aras daya suara dalam akustik,[58] serta mengukur penyerapan cahaya dalam bidang spektrometri dan optika. Selain itu, desibel juga dipakai dalam nisbah sinyal-derau yang menjelaskan seberapa banyak derau dibandingkan dengan sinyal yang berguna.[59] Mirip dengan tadi, nisbah puncak sinyal-derau biasanya dipakai menilai kualitas suara dan metode pemampatan citra melalui logaritma.[60]
Kekuatan gempa bumi diukur dengan mengambil logaritma umum dari energi yang dipancarkan saat terjadinya gempa dalam satuan skala magnitudo momen atau skala magnitudo Ritcher. Sebagai contoh, gempa berkekuatan 5,0 melepaskan 32 kali (101,5) dan gempa berkekuatan 6,0 melepaskan 1000 kali(103) energi berkekuatan 4,0.[61] Skala logaritmik juga dipakai dalam magnitudo kentara untuk mengukur kecerahan bintang.[62] Dalam kimia, negatif dari logaritma desimal, yang disebut sebagai kologaritma desimal, ditunjukkan dengan huruf "p".[63] Sebagai contoh, pH merupakan kologaritma desimal dari keaktifan dari ion berbentuk hidrogen H+ yang terbentuk dari air, hidronium.[64] Keaktifan dari ion hidronium dalam air yang netral bernilai 10−7 mol·L−1, sehingga nilai pH adalah 7. Contoh lainnya, nilai pH dari asam cuka biasanya sekitar 3. Perbedaan nilai sebesar 4 sesuai dengan rasio 104 berdasarkan aktivitasnya, yaitu nilai dari aktivitas ion hidronium cuka sekitar 10−3 mol·L−1.
Konsep skala logaritmik dapat dipakai dalam grafik (log-linear) semilog bertujuan untuk memberikan visual terkait satu sumbu, yang biasanya berupa sumbu vertikal, diukur menggunakan perhitungan logaritma. Contohnya seperti grafik disamping menjelaskan nilai yang menaik dengan tajam dari 1 juta hingga 1 triliun ke dalam ruang yang sama (pada sumbu vertikal) saat grafiknya menaik dari 1 hingga 1 juta. Pada grafik tersebut, fungsi eksponensial f(x) = a · bx muncul sebagai garis lurus dengan kemiringan yang sama dengan logaritma dari b. Selain itu, skala logaritma yang dapat dipakai dalam grafik log-log untuk mengukur sumbu vertikal dan horizontal, sehingga menyebabkan fungsi f(x) = a · xk digambarkan sebagai garis lurus yang mempunyai kemiringan yang sama dengan bilangan yang dipangkat dengan k, diterapkan pada saat memberikan visual dan menganalisis hukum pangkat.[65]
Penerapannya dalam psikologi
[sunting | sunting sumber]Penerapan logaritma juga terdapat dalam beberapa hukum yang menjelaskan tentang persepsi manusia.[66][67] Sebagai contoh, hukum Hick menjelaskan kaitan logaritmik antara waktu saat orang mengambil keputusan beserta jumlah keputusan yang dimiliki.[68] Hukum lainnya adalah hukum Fitts, yang memprediksi bahwa waktu yang diperlukan saat bergerak ke daerah target dengan cepat sama dengan fungsi logaritmik dari jarak dan ukuran target.[69] Dalam psikofisika, hukum Weber–Fechner mengatakan kaitan logaritmik dengan stimulus dan sensasi yang dirasakan, contohnya seperti saat orang sedang membawa berat benda yang sesungguhnya dengan yang dirasakan.[70] (Namun, "hukum" ini kurang realistis dengan model belakangan ini, seperti hukum perpangkatan Stevens.[71])
Studi psikologi menemukan bahwa orang yang sedikit mempunyai pemahaman matematika cenderung mengestimasi nilai kuantitas dengan logaritma, atau dengan kata lain, bilangannya ditempatkan pada garis yang tidak ditandai berdasarkan perhitungan logaritma, sehingga 10 yang ditempatkan mendekati 100 dianggap sebagai 100 yang ditempatkan mendekati 1000. Orang yang memiliki pemahaman yang lebih tinggi memandang hal tersebut sebagai linear yang mengestimasi (letak angka 1000 yang berjarak 10 kali lebih jauh) pada beberapa kasus, namun logaritma dipakai pada saat memplot bilangan-bilangan yang sulit untuk diplotkan secara linear.[72][73]
Penerapannya dalam teori peluang dan statistika
[sunting | sunting sumber]Dalam teori probabilitas, hukum bilangan besar mengatakan bahwa, untuk sebuah mata uang seimbang, ketika jumlah pelemparan koin naik menuju takhingga, maka kesebandingan dari gambar kepala (atau ekor) yang diamati mendekati satu setengah. Fluktuasi dari nilai kesebandingan yang bernilai satu setengah dijelaskan melalui hukum yang menggunakan logaritma, yaitu hukum logaritma teriterasi.[74]
Logaritma muncul pula dalam sebaran log-normal. Ketika logaritma dari variabel acak mempunyai sebaran normal, maka variabel dikatakan mempunyai sebaran log-normal.[75] Sebaran log-normal ditemukan dalam banyak bidang, dengan suatu variabel dibentuk sebagai hasil kali dari banyaknya variabel acak indenpenden bernilai positif. Contohnya seperti dalam mempelajari turbulensi.[76]
Logaritma dipakai untuk menghitung estimasi kemungkinan maksimum dari model statistika parametrik. Fungsi kemungkinan pada model tersebut bergantung setidaknya satu parameter yang harus diestimasi. Nilai maksimum dari fungsi kemungkinan muncul di nilai parameter yang sama sebagai nilai maksimum logaritma kemungkinan (atau disebut log likelihood), karena logaritma merupakan fungsi menaik. Log-likelihood adalah teknik yang memaksimumkan fungsi dengan mudah, khususnya untuk kemungkinan yang dikali mengenai variabel acak independen.[77]
Hukum Benford menjelaskan kemungkinan digit dalam himpunan data yang banyak, contohnya seperti tinggi bangunan. Menurut hukum Benford, kemungkinan bahwa digit desimal pertama suatu item dalam sampel data adalah d (yang berkisar dari 1 hingga 9) sama dengan 10log (d + 1) − 10log (d), tanpa memperhatikan satuan pengukuran.[78] Jadi, sekitar 30% data dapat diduga mempunyai 1 sebagai digit pertama, 18% dimulai dengan 2, dst. Penyimpangan dari hukum Benford dihitung oleh para akuntan untuk membantu mendeteksi penipuan data akuntansi.[79]
Penerapannya dalam kompleksitas perhitungan
[sunting | sunting sumber]Cabang dalam ilmu komputer yang mempelajari performa dari suatu algoritma dalam menyelesaikan persoalan atau masalah tertentu disebut analisis algoritma.[80] Logaritma sangat penting dalam menjelaskan algoritma tersebut dengan membagi suatu masalah menjadi lebih kecil, serta menghubungkan penyelesaian dari submasalah.[81]
Sebagai contoh, cara algoritma pencarian biner (bahasa Inggris: binary searching algorithm) dalam mencari bilangan dalam daftar yang tersortir adalah dengan memeriksa entri tengah dan meneruskannya di sebagian sebelum atau sesudah entri tengah jika tidak ditemukan bilangannya. Umumnya, algoritma ini memerlukan perbandingan 2log (N), dengan N adalah panjang daftar.[82] Mirip dengan sebelumnya, algoritma urut gabungan menyortir daftar yang belum tersortir dengan membagi daftar menjadi setengah bagian dan mengurutkan daftar-daftar tersebut dahulu sebelum menggabungkan hasilnya. Algoritma urut gabungan biasanya memerlukan waktu yang kira-kira sebanding dengan N · log(N).[83] Bilangan pokok logaritma tidak dijelaskan secara spesifik, karena hasilnya hanya berubah oleh faktor konstanta saat ada bilangan pokok lain yang sedang dipakai. Faktor konstanta biasanya diabaikan dalam analisis algoritma dalam model biaya seragam (bahasa Inggris: uniform cost model) yang standar.[84]
Suatu fungsi f(x) dikatakan bertumbuh secara logaritmik jika f(x) (setidaknya atau kira-kira) sebanding dengan logaritma dari x, namun istilah ini dipakai sebagai fungsi eksponensial dalam menjelaskan pertumbuhan organisme secara biologis.[85] Sebagai contoh, setiap bilangan asli N dapat direpresentasikan dalam bentuk bilangan biner yang tidak lebih dari 2log N + 1 bit. Dengan kata lain, jumlah memori diperlukan untuk menyimpan N pertumbuhan secara logaritmik dengan N.
Penerapannya dalam entropi dan ketidakteraturan
[sunting | sunting sumber]
Entropi secara umum adalah ukuran dari ketidakteraturan dari suatu sistem. Dalam termodinamika statistik, sebuah entropi, disimbolkan dengan S, dari sebuah sistem, didefinisikan dengan:
Hasilnya adalah seluruh kondisi i yang mungkin dari sistem yang dimaksud, contoh posisi dari partikel gas di dalam sebuah tangki. Lebih lanjut lagi, pi adalah kemungkinan bahwa kondisi i telah tercapai dan k adalah konstanta Boltzmann. Sama halnya dengan entropi dalam teori informasi yang mengukur kuantitas dari informasi. Jika penerima pesan mengharapkan sejumlah N pesan yang mungkin diterima dengan besar kemungkinan masing-masing yang setara, maka sejumlah informasi yang tersampaikan oleh pesan tersebut dapat dikuantifikasi dengan bit 2log N.[86]
Eksponen Lyapunov menggunakan logaritma untuk mengukur derajat ketidakteraturan dari sistem yang dinamis. Contoh partikel yang bergerak di meja biliar oval, di mana bahkan perubahan sekecil apapun dari kondisi awal dapat memberikan hasil, yaitu jalur yang dilalui, yang sangat berbeda. Sistem yang dimaksud disebut dengan kekacauan di dalam sistem deterministik karena galat yang kecil namun terukur dari kondisi awal dapat diprediksi akan memberikan hasil akhir yang sangat berbeda.[87] Setidaknya satu eksponen Lyapunov dari sistem kekacauan yang deterministik akan bernilai positif.
Penerapannya dalam bangunan fraktal
[sunting | sunting sumber]
Logaritma muncul dalam definiisi dimensi fraktal.[88] Fraktal merupakan benda-benda geometri yang menyerupai dirinya, dalam artian bahwa benda geometri tersebut mereproduksi dirinya lebih kecil, penjelasan kasarnya, di seluruh strukturnya. Contohnya seperti segitiga Sierpiński, dengan dimensi Hausdorffnya adalah ln(3)ln(2) ≈ 1,58, dapat diliputi dengan tiga salinan dirinya, masing-masing sisinya dibagi menjadi setengah dari panjang awalnya. Adapula gagasan dimensi fraktal berdasarkan logaritma lainnya diperoleh dengan menghitung jumlah kotak yang diperlukan untuk meliputi frakal dalam himpunan.
Penerapannya dalam musik
[sunting | sunting sumber]Logaritma berkaitan dengan bunyi nada dan interval dalam musik. Dalam temperamen sama, perbandingan frekuensi bergantung pada interval di antara dua nada saja, bukan pada frekuensi yang spesifik atau tinggi dari nada tunggal. Sebagai contoh, nada A mempunyai frekuensi 440 Hz dan B-flat mempunyai frekuensi 466 Hz. Interval antara nada A dengan B-flat ini digolongkan sebagai semi-nada, karena intervalnya berada di antara B-flat dan B (yang mempunyai frekuensi 493 Hz). Maka, perbandingan frekuensinya adalah:
Peran logaritma dalam musik dapat dipakai untuk menjelaskan interval berikut: suatu interval diukur dalam semi-nada dengan mengambil logaritma dengan bilangan pokok-21/12 dari perbandingan frekuensi, sedangkan logaritma dengan bilangan pokok-21/1200 dari perbandingan frekuensi menyatakan interval dalam sen, ratusan semi-nada. Logaritma yang terakhir dipakai untuk pengodean yang lebih halus, karena diperlukan untuk temperamen tak sama.[89]
| Interval (dua bunyi nada yang dimainkan dalam waktu yang sama) | Bunyi nada 1/12 ⓘ | Semi-nada ⓘ | Just major third ⓘ | Major third ⓘ | Tritone ⓘ | Oktaf ⓘ |
| Rasio frekuensi r | ||||||
| Jumlah semi-nada yang sama | ||||||
| Jumlah sen yang sama |
Penerapannya dalam teori bilangan
[sunting | sunting sumber]Logaritma alami sangat berkaitan dengan salah satu topik dalam teori bilangan, yaitu menghitung bilangan prima. Untuk setiap bilangan bulat x, jumlah bilangan prima kurang dari sama dengan x dinyatakan sebagai π(x). Teorema bilangan prima mengatakan bahwa π(x) kira-kira sama dengan
yang berarti bahwa fungsi pencacahan bilangan prima kira-kira sama dengan perbandingan dari π(x) dan pecahan yang mendekati 1 ketika x menuju ke takhingga.[90] Akibatnya, peluang dari bilangan yang dipilih secara acak di antara 1 dan x adalah bilangan prima berbanding terbalik dengan jumlah digit desimal x. Pendekatan π(x) yang lebih baik merupakan fungsi integral Euler Li(x), yang didefinisikan sebagai
Hipotesis Riemann, yang merupakan salah satu konjektur matemtika terbuka yang paling terlama, dapat dinyatakan dalam bentuk perbandingan π(x) dan Li(x).[91] Teorema Erdős–Kac mengatakan bahwa jumlah faktor bilangan prima yang berbeda juga melibatkan logaritma alami.
Logaritma dari n faktorial, n! = 1 · 2 · ... · n, dirumuskan sebagai
Rumus di atas dapat dipakai utnuk memperoleh sebuah hampiran dari n! untuk setiap bilangan n yang lebih besar, yaitu rumus Stirling.[92]
Perumuman
[sunting | sunting sumber]Logaritma kompleks
[sunting | sunting sumber]Semua bilangan kompleks a yang menyelesaikan persamaan
disebut logaritma kompleks dari z, ketika z (dianggap sebagai) bilangan kompleks. Bilangan kompleks biasanya dinyatakan sebagai z = x + iy, dengan x dan y adalah bilangan real dan i adalah satuan imajiner (satuan yang dikuadratkan memberikan nilai −1). Bilangan kompleks dapat divisualisasikan melalui sebuah titik dalam bidang kompleks, seperti yang diperlihatkan pada gambar berikut. Bentuk polar menulis bilangan kompleks tak-nol z melalui titik nilai mutlak, yang berarti jarak yang berupa bilangan bernilai real dan positif r sama dengan titik z ke titik asalnya. Bentuk polar juga menulis sebuah sudut antara bilangan real pada sumbu-Re (yakni sumbu-x) Re dan garis yang melalui titik asal dan titik z. Sudut tersebut disebut sebagai argumen dari z.

Nilai mutlak r dari z dinyatakan sebagai
Dengan menggunakan pandangan geometris pada fungsi sinus dan kosinus beserta periodisitasnya dalam 2π, setiap bilangan kompleks z dapat dinyatakan sebagai
untuk setiap bilangan bulat k. Nyatanya, argumen dari z tidak dijelaskan secara unik, yakni: bilangan φ dan φ' = φ + 2kπ adalah argumen valid dari z untuk semua bilangan bulat k, karena menambahkan 2kπ radian atau k⋅360°[nb 6] ke bilangan φ berpadanan dengan "lilitan" di sekitar titik asal yang berputar berlawanan arah jarum jam sebanyak k putaran. Hasil bilangan kompleks selalu z, seperti yang diilustrasikan pada gambar untuk k = 1. Setidaknya ada salah satu dari argumen z yang mungkin disebut sebagai argumen prinsip, yang dilambangkan Arg(z), dipilih dengan memerlukan putaran φ di selang (−π, π][93] atau [0, 2π).[94] Daerah-daerah tersebut, dengan argumen z ditentukan sekali disebut cabang dari fungsi argumen.
Rumus Euler mengaitkan fungsi trigonometri sinus dan kosinus dengan eksponensial kompleks:
Dengan menggunakan rumus di atas, dan periodisitasnya lagi, maka berlaku identitas berikut:[95]
dengan ln(r) adalah fungsi logaritma real tunggal, ak menyatakan logaritma kompleks dari z, dan k bilangan bulat sembarang. Karena itu, logaritma kompleks dari z, yang semua bilangan kompleks ak untuk e pangkat ak sama dengan z, mempunyai tak berhingga banyaknya nilai
- untuk bilangan bulat sembarang k.

Dengan mengambil k sehingga φ + 2kπ ada di dalam selang yang ditentukan untuk argumen prinsip, maka ak disebut nilai prinsip dari logaritma, dinotasikan sebagai Log(z). Argumen prinsip setiap bilangan real positif x bernilai 0, jadi Log(x) adalah sebuah bilangan real yang sama dengan logaritma (alami). Akan tetapi, rumus logaritma tentang darab dan perpangkatan bilangan di atas tidak memberikan perumuman terkait nilai prinsip dari logaritma kompleks.[96]
Ilustrasi tersebut menggambarkan Log(z), membatasi argumen z dengan interval (−π, π]. Cara memadankan cabang dari logaritma kompleks mempunyai ketakkontinuan di sepanjang sumbu-x real negatif, seperti yang dapat dilihat pada lompatan hue di gambar. Saat melintasi batas, ketakkontinuan tersebut dimulai dari lompatan hingga batas lain yang ada di cabang yang sama, dalam artian bahwa tiada perubahan dengan nilai-k dari cabang tetangga kontinu yang berpadanan. Lokus tersebut dinamakan potongan cabang. Dengan menghapus perbatasan argumen, maka relasi "argumen dari z" dan "logaritma dari z" menjadi fungsi bernilai banyak.
Kebalikan dari fungsi eksponensial lainnya
[sunting | sunting sumber]Eksponensiasi muncul dalam cabang matematika dan fungsi inversnya seringkali mengacu pada logaritma. Sebagai contoh, logaritma matriks merupakan fungsi invers (bernilai banyak) dari eksponensial matriks.[97] Contohnya lain seperti fungsi logaritma p-adic, fungsi invers dari fungsi eksponensial p-adic. Kedua fungsi tersebut didefinisikan melalui deret Taylor yang analog dengan kasus bilangan real.[98] Dalam konteks geometri diferensial, peta eksponensial memetakan ruang garis singgung di sebuah titik lipatan ke lingkungan titik tersebut. Kebalikannya juga disebut peta logaritma.[99]
Dalam konteks grup hingga, eksponensiasi dinyatakan dengan mengalikan satu anggota grup b dengan dirinya secara berulang. Logaritma diskret merupakan bilangan bulat n yang menyelesaikan persamaan
dengan x adalah anggota dari grup. Mengerjakan solusi eksponensiasi dapat dilakukan dengan efisien, namun logaritma diskret dipercayai bahwa sangat sulit untuk menghitungnya dalam beberapa grup. Asimetri dari grup tersebut mempunyai penerapan penting dalam kriptografi kunci publik, contohnya seperti pertukaran kunci Diffie–Hellman, sebuah pertukaran kunci sehari-hari yang memungkinkan pertukaran kunci kriptografi terhadap saluran informasi yang tidak diamankan.[100] Logaritma Zech berkaitan dengan logaritma diskret dalam grup perkalian anggota taknol dari medan hingga.[101]
Adapun fungsi invers berupa logaritma lainnya. Fungsi tersebut di antaranya: logaritma ganda ln(ln(x)) yang merupakan kebalikan dari fungsi eksponensial ganda, superlogaritma yang merupakan kebalikan dari tetrasi, fungsi Lambert W yang merupakan kebalikan dari fungsi f(w) = wew,[102] dan logit yang merupakan kebalikan dari fungsi logistik.[103]
Konsep yang berkaitan
[sunting | sunting sumber]Berdasarkan sudut pandang teori grup, identitas log(cd) = log(c) + log(d) menyatakan isomorfisme grup antara bilangan riil positif terhadap perkalian bilangan riil positif terhadap penambahan. Fungsi logaritmik hanya isomorfisme kontinu antara grup.[104] Berdasarkan pengertian isomorfisme tersebut, ukuran Haar (ukuran Lebesgue) dx pada riil berpadanan dengan ukuran Haar dxx pada bilangan real positif.[105] Bilangan riil taknegatif tidak hanya terhadap operasi perkalian, namun juga terhadap operasi penambahan, dan bilangan riil taknegatif membentuk semigelanggang, yang disebut sebagai semigelanggang probabilitas, bahkan membentuk semigelanggang. Maka logaritma yang mengambil perkalian dengan penambahan (perkalian logaritma), dan mengambil penambahan dengan penambahan logaritma, memberikan isomorfisme semigelanggang di antara semigelanggang probabilitas dan semigelanggang logaritma.
Konsep ini juga terdapat di dalam analisis kompleks dan geometri aljabar, yang logaritmik satu bentuk df/f adalah bentuk diferensial dengan pole logaritmik.[106]
Selain itu, terdapat polilogaritma, sebuah fungsi yang didefinisikan sebagai
Fungsi ini mempunyai kaitan dengan logaritma alami dengan Li1 (z) = −ln(1 − z). Terlebih lagi, ketika z = 1, nilai dari Lis (1) sama dengan fungsi zeta Riemann, yang dinyatakan sebagai ζ(s).[107]
Lihat pula
[sunting | sunting sumber]Catatan
[sunting | sunting sumber]- ^ Perbatasan x dan b dijelaskan pada bagian "Sifat analitik".
- ^ Beberapa para matematikawan menolak notasi ini. Dalam otobiografinya pada tahun 1985, Paul Halmos mengkritik bahwa "notasi ln bersifat kekanak-kanakan", karena menurutnya para matematikawan menggunakan notasi tersebut.[15] Notasi tersebut ditemukan oleh seorang matematikawan bernama Irving Stringham.[16][17]
- ^ Contohnya seperti C, Java, Haskell, and BASIC.
- ^ Deret yang sama berlaku untuk nilai utama dari logaritma kompleks untuk bilangan kompleks z yang memenuhi |z − 1| < 1.
- ^ Deret yang sama berlaku untuk nilai utama dari logaritma kompleks untuk bilangan kompleks z dengan bagian real positif.
- ^ Lihat radian untuk konversi antara 2π dengan 360 derajat.
Referensi
[sunting | sunting sumber]- ^ Hobson, Ernest William (1914), John Napier and the invention of logarithms, 1614; a lecture, University of California Libraries, Cambridge : University Press
- ^ Remmert, Reinhold. (1991), Theory of complex functions, New York: Springer-Verlag, ISBN 0387971955, OCLC 21118309
- ^ Kate, S.K.; Bhapkar, H.R. (2009), Basics Of Mathematics, Pune: Technical Publications, ISBN 978-81-8431-755-8[pranala nonaktif permanen], chapter 1
- ^ Semua pernyataan di bagian ini dapat ditemukan pada Shailesh Shirali 2002, bagian 4. Sebagai contoh, (Douglas Downing 2003, hlm. 275), atau Kate & Bhapkar 2009, hlm. 1-1.
- ^ Bernstein, Stephen; Bernstein, Ruth (1999), Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-005023-5, hlm. 21
- ^ Downing, Douglas (2003), Algebra the Easy Way, Barron's Educational Series, Hauppauge, NY: Barron's, ISBN 978-0-7641-1972-9, chapter 17, hlm. 275
- ^ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-0, hlm. 20
- ^ Van der Lubbe, Jan C. A. (1997), Information Theory, Cambridge University Press, hlm. 3, ISBN 978-0-521-46760-5
- ^ Allen, Elizabeth; Triantaphillidou, Sophie (2011), The Manual of Photography, Taylor & Francis, hlm. 228, ISBN 978-0-240-52037-7
- ^ Quantities and units–Part 2: Mathematics (ISO 80000-2:2019); EN ISO 80000-2
- ^ Goodrich, Michael T.; Tamassia, Roberto (2002), Algorithm Design: Foundations, Analysis, and Internet Examples, John Wiley & Sons, hlm. 23
Terjemahan:One of the interesting and sometimes even surprising aspects of the analysis of data structures and algorithms is the ubiquitous presence of logarithms ... As is the custom in the computing literature, we omit writing the base b of the logarithm when b = 2.
Salah satu hal yang menarik dan terkadang yang paling mengejutkan dalam aspek dari analisis struktur data beserta algoritma adalah bahwa keberadaan logaritma ada dimana-mana ... Menjadi kebiasaan dalam literatur komputer, kita menghilangkan penulisan bilangan pokok b dari logaritma ketika b = 2.
- ^ Parkhurst, David F. (2007), Introduction to Applied Mathematics for Environmental Science (edisi ke-illustrated), Springer Science & Business Media, hlm. 288, ISBN 978-0-387-34228-3
- ^ Gullberg, Jan (1997), Mathematics: from the birth of numbers.
 , New York: W. W. Norton & Co, ISBN 978-0-393-04002-9
, New York: W. W. Norton & Co, ISBN 978-0-393-04002-9
- ^ See footnote 1 in Perl, Yehoshua; Reingold, Edward M. (December 1977), "Understanding the complexity of interpolation search", Information Processing Letters, 6 (6): 219–22, doi:10.1016/0020-0190(77)90072-2
- ^ Paul Halmos (1985), I Want to Be a Mathematician: An Automathography, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96078-4
- ^ Irving Stringham (1893), Uniplanar algebra: being part I of a propædeutic to the higher mathematical analysis, The Berkeley Press, hlm. xiii
- ^ Roy S. Freedman (2006), Introduction to Financial Technology, Amsterdam: Academic Press, hlm. 59, ISBN 978-0-12-370478-8
- ^ Lihat Teorema 3.29 di Rudin, Walter (1984), Principles of mathematical analysis (edisi ke-3rd ed., International student), Auckland: McGraw-Hill International, ISBN 978-0-07-085613-4
- ^ Napier, John (1614), Mirifici Logarithmorum Canonis Descriptio [The Description of the Wonderful Rule of Logarithms] (dalam bahasa Latin), Edinburgh, Scotland: Andrew Hart
- ^ Hobson, Ernest William (1914), John Napier and the invention of logarithms, 1614, Cambridge: The University Press
- ^ Folkerts, Menso; Launert, Dieter; Thom, Andreas (2016), "Jost Bürgi's method for calculating sines", Historia Mathematica, 43 (2): 133–147, arXiv:1510.03180
 , doi:10.1016/j.hm.2016.03.001, MR 3489006
, doi:10.1016/j.hm.2016.03.001, MR 3489006
- ^ O'Connor, John J.; Robertson, Edmund F., "Jost Bürgi (1552–1632)", Arsip Sejarah Matematika MacTutor, Universitas St Andrews.
- ^ William Gardner (1742) Tables of Logarithms
- ^ Pierce, R. C. Jr. (January 1977), "A brief history of logarithms", The Two-Year College Mathematics Journal, 8 (1): 22–26, doi:10.2307/3026878, JSTOR 3026878
- ^ Enrique Gonzales-Velasco (2011) Journey through Mathematics–Creative Episodes in its History, §2.4 Hyperbolic logarithms, hlm. 117, Springer ISBN 978-0-387-92153-2
- ^ Florian Cajori (1913) "History of the exponential and logarithm concepts", American Mathematical Monthly 20: 5, 35, 75, 107, 148, 173, 205.
- ^ Stillwell, J. (2010), Mathematics and Its History (edisi ke-3), Springer
- ^ Bryant, Walter W. (1907), A History of Astronomy, London: Methuen & Co, hlm. 44
Teks asli:"...[a]n admirable artifice which, by reducing to a few days the labour of many months, doubles the life of the astronomer, and spares him the errors and disgust inseparable from long calculations."
- ^ Abramowitz, Milton; Stegun, Irene A., ed. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (edisi ke-10th), New York: Dover Publications, ISBN 978-0-486-61272-0, bagian 4.7., hlm. 89
- ^ Campbell-Kelly, Martin (2003), The history of mathematical tables: from Sumer to spreadsheets, Oxford scholarship online, Oxford University Press, ISBN 978-0-19-850841-0, bagian 2
- ^ Spiegel, Murray R.; Moyer, R.E. (2006), Schaum's outline of college algebra, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-145227-4, hlm. 264
- ^ Maor, Eli (2009), E: The Story of a Number, Princeton University Press, bagian 1, 13, ISBN 978-0-691-14134-3
- ^ Devlin, Keith (2004), Sets, functions, and logic: an introduction to abstract mathematics, Chapman & Hall/CRC mathematics (edisi ke-3rd), Boca Raton, Fla: Chapman & Hall/CRC, ISBN 978-1-58488-449-1, atau lihat referensinya di fungsi.
- ^ a b Lang, Serge (1997), Undergraduate analysis, Undergraduate Texts in Mathematics (edisi ke-2nd), Berlin, New York: Springer-Verlag, doi:10.1007/978-1-4757-2698-5, ISBN 978-0-387-94841-6, MR 1476913, bagian III.3
- ^ a b Lang 1997, bagian IV.2
- ^ Dieudonné, Jean (1969), Foundations of Modern Analysis, 1, Academic Press, hlm. 84 item (4.3.1)
- ^ "Calculation of d/dx(Log(b,x))", Wolfram Alpha, Wolfram Research, diakses tanggal 15 Maret 2011
- ^ Kline, Morris (1998), Calculus: an intuitive and physical approach, Dover books on mathematics, New York: Dover Publications, ISBN 978-0-486-40453-0, hlm. 386
- ^ "Calculation of Integrate(ln(x))", Wolfram Alpha, Wolfram Research, diakses tanggal 15 Maret 2011
- ^ Abramowitz & Stegun, eds. 1972, hlm. 69
- ^ Courant, Richard (1988), Differential and integral calculus. Vol. I, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-60842-4, MR 1009558, bagian III.6
- ^ Havil, Julian (2003), Gamma: Exploring Euler's Constant, Princeton University Press, ISBN 978-0-691-09983-5, bagian 11.5 dan 13.8
- ^ Nomizu, Katsumi (1996), Selected papers on number theory and algebraic geometry, 172, Providence, RI: AMS Bookstore, hlm. 21, ISBN 978-0-8218-0445-2
- ^ Baker, Alan (1975), Transcendental number theory, Cambridge University Press, ISBN 978-0-521-20461-3, hlm. 10
- ^ Muller, Jean-Michel (2006), Elementary functions (edisi ke-2nd), Boston, MA: Birkhäuser Boston, ISBN 978-0-8176-4372-0, bagian 4.2.2 (hlm. 72) dan 5.5.2 (hlm. 95)
- ^ Hart; Cheney; Lawson; et al. (1968), Computer Approximations, SIAM Series in Applied Mathematics, New York: John Wiley, bagian 6.3, hlm. 105–11
- ^ Zhang, M.; Delgado-Frias, J.G.; Vassiliadis, S. (1994), "Table driven Newton scheme for high precision logarithm generation", IEE Proceedings - Computers and Digital Techniques, 141 (5): 281–92, doi:10.1049/ip-cdt:19941268, ISSN 1350-2387, bagian 1 for an overview
- ^ Meggitt, J.E. (April 1962), "Pseudo Division and Pseudo Multiplication Processes", IBM Journal of Research and Development, 6 (2): 210–26, doi:10.1147/rd.62.0210
- ^ Kahan, W. (20 May 2001), Pseudo-Division Algorithms for Floating-Point Logarithms and Exponentials
- ^ a b Abramowitz & Stegun, eds. 1972, hlm. 68
- ^ Sasaki, T.; Kanada, Y. (1982), "Practically fast multiple-precision evaluation of log(x)", Journal of Information Processing, 5 (4): 247–50, diakses tanggal 30 Maret 2011
- ^ Ahrendt, Timm (1999), "Fast Computations of the Exponential Function", Stacs 99, Lecture notes in computer science, 1564, Berlin, New York: Springer, hlm. 302–12, doi:10.1007/3-540-49116-3_28, ISBN 978-3-540-65691-3
- ^ Hillis, Danny (15 January 1989), "Richard Feynman and The Connection Machine", Physics Today, 42 (2): 78, Bibcode:1989PhT....42b..78H, doi:10.1063/1.881196
- ^ Maor 2009, hlm. 135
- ^ Frey, Bruce (2006), Statistics hacks, Hacks Series, Sebastopol, CA: O'Reilly, ISBN 978-0-596-10164-0, bab 6, bagian 64
- ^ Ricciardi, Luigi M. (1990), Lectures in applied mathematics and informatics, Manchester: Manchester University Press, ISBN 978-0-7190-2671-3, hlm. 21, bagian 1.3.2
- ^ Bakshi, U.A. (2009), Telecommunication Engineering, Pune: Technical Publications, ISBN 978-81-8431-725-1[pranala nonaktif permanen], bagian 5.2
- ^ Maling, George C. (2007), "Noise", dalam Rossing, Thomas D., Springer handbook of acoustics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-30446-5, bagian 23.0.2
- ^ Tashev, Ivan Jelev (2009), Sound Capture and Processing: Practical Approaches, New York: John Wiley & Sons, hlm. 98, ISBN 978-0-470-31983-3
- ^ Chui, C.K. (1997), Wavelets: a mathematical tool for signal processing, SIAM monographs on mathematical modeling and computation, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-384-8
- ^ Crauder, Bruce; Evans, Benny; Noell, Alan (2008), Functions and Change: A Modeling Approach to College Algebra (edisi ke-4th), Boston: Cengage Learning, ISBN 978-0-547-15669-9, bagian 4.4.
- ^ Bradt, Hale (2004), Astronomy methods: a physical approach to astronomical observations, Cambridge Planetary Science, Cambridge University Press, ISBN 978-0-521-53551-9, bagian 8.3, hlm. 231
- ^ Nørby, Jens (2000). "The origin and the meaning of the little p in pH". Trends in Biochemical Sciences. 25 (1): 36–37. doi:10.1016/S0968-0004(99)01517-0. PMID 10637613.
- ^ IUPAC (1997), A. D. McNaught, A. Wilkinson, ed., Compendium of Chemical Terminology ("Gold Book") (edisi ke-2nd), Oxford: Blackwell Scientific Publications, doi:10.1351/goldbook
 , ISBN 978-0-9678550-9-7
, ISBN 978-0-9678550-9-7
- ^ Bird, J.O. (2001), Newnes engineering mathematics pocket book (edisi ke-3rd), Oxford: Newnes, ISBN 978-0-7506-4992-6, bagian 34
- ^ Goldstein, E. Bruce (2009), Encyclopedia of Perception, Encyclopedia of Perception, Thousand Oaks, CA: Sage, ISBN 978-1-4129-4081-8, hlm. 355–56
- ^ Matthews, Gerald (2000), Human Performance: Cognition, Stress, and Individual Differences, Hove: Psychology Press, ISBN 978-0-415-04406-6, hlm. 48
- ^ Welford, A.T. (1968), Fundamentals of skill, London: Methuen, ISBN 978-0-416-03000-6, OCLC 219156, hlm. 61
- ^ Paul M. Fitts (June 1954), "The information capacity of the human motor system in controlling the amplitude of movement", Journal of Experimental Psychology, 47 (6): 381–91, doi:10.1037/h0055392, PMID 13174710 , reprinted in Paul M. Fitts (1992), "The information capacity of the human motor system in controlling the amplitude of movement" (PDF), Journal of Experimental Psychology: General, 121 (3): 262–69, doi:10.1037/0096-3445.121.3.262, PMID 1402698, diakses tanggal 30 March 2011
- ^ Banerjee, J.C. (1994), Encyclopaedic dictionary of psychological terms, New Delhi: M.D. Publications, hlm. 304, ISBN 978-81-85880-28-0, OCLC 33860167
- ^ Nadel, Lynn (2005), Encyclopedia of cognitive science, New York: John Wiley & Sons, ISBN 978-0-470-01619-0, lemmas Psychophysics and Perception: Overview
- ^ Siegler, Robert S.; Opfer, John E. (2003), "The Development of Numerical Estimation. Evidence for Multiple Representations of Numerical Quantity" (PDF), Psychological Science, 14 (3): 237–43, CiteSeerX 10.1.1.727.3696
 , doi:10.1111/1467-9280.02438, PMID 12741747, diarsipkan dari versi asli (PDF) tanggal 17 May 2011, diakses tanggal 7 January 2011
, doi:10.1111/1467-9280.02438, PMID 12741747, diarsipkan dari versi asli (PDF) tanggal 17 May 2011, diakses tanggal 7 January 2011
- ^ Dehaene, Stanislas; Izard, Véronique; Spelke, Elizabeth; Pica, Pierre (2008), "Log or Linear? Distinct Intuitions of the Number Scale in Western and Amazonian Indigene Cultures", Science, 320 (5880): 1217–20, Bibcode:2008Sci...320.1217D, CiteSeerX 10.1.1.362.2390
 , doi:10.1126/science.1156540, PMC 2610411
, doi:10.1126/science.1156540, PMC 2610411  , PMID 18511690
, PMID 18511690
- ^ Breiman, Leo (1992), Probability, Classics in applied mathematics, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-296-4, bagian 12.9
- ^ Aitchison, J.; Brown, J.A.C. (1969), The lognormal distribution, Cambridge University Press, ISBN 978-0-521-04011-2, OCLC 301100935
- ^ Jean Mathieu and Julian Scott (2000), An introduction to turbulent flow, Cambridge University Press, hlm. 50, ISBN 978-0-521-77538-0
- ^ Rose, Colin; Smith, Murray D. (2002), Mathematical statistics with Mathematica, Springer texts in statistics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-95234-5, bagian 11.3
- ^ Tabachnikov, Serge (2005), Geometry and Billiards, Providence, RI: American Mathematical Society, hlm. 36–40, ISBN 978-0-8218-3919-5, bagian 2.1
- ^ Durtschi, Cindy; Hillison, William; Pacini, Carl (2004), "The Effective Use of Benford's Law in Detecting Fraud in Accounting Data" (PDF), Journal of Forensic Accounting, V: 17–34, diarsipkan dari versi asli (PDF) tanggal 29 Agustus 2017, diakses tanggal 28 Mei 2018
- ^ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-0, hlm. 1–2
- ^ Harel, David; Feldman, Yishai A. (2004), Algorithmics: the spirit of computing, New York: Addison-Wesley, ISBN 978-0-321-11784-7, hlm. 143
- ^ Knuth, Donald (1998), The Art of Computer Programming, Reading, MA: Addison-Wesley, ISBN 978-0-201-89685-5, bagian 6.2.1, hlm. 409–26
- ^ Donald Knuth 1998, bagian 5.2.4, hlm. 158–68
- ^ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, hlm. 20, ISBN 978-3-540-21045-0
- ^ Mohr, Hans; Schopfer, Peter (1995), Plant physiology
 , Berlin, New York: Springer-Verlag, ISBN 978-3-540-58016-4, bab 19, hlm. 298
, Berlin, New York: Springer-Verlag, ISBN 978-3-540-58016-4, bab 19, hlm. 298
- ^ Eco, Umberto (1989), The open work, Harvard University Press, ISBN 978-0-674-63976-8, bagian III.I
- ^ Sprott, Julien Clinton (2010), "Elegant Chaos: Algebraically Simple Chaotic Flows", Elegant Chaos: Algebraically Simple Chaotic Flows. Edited by Sprott Julien Clinton. Published by World Scientific Publishing Co. Pte. Ltd, New Jersey: World Scientific, Bibcode:2010ecas.book.....S, doi:10.1142/7183, ISBN 978-981-283-881-0, bagian 1.9
- ^ Helmberg, Gilbert (2007), Getting acquainted with fractals, De Gruyter Textbook, Berlin, New York: Walter de Gruyter, ISBN 978-3-11-019092-2
- ^ Wright, David (2009), Mathematics and music, Providence, RI: AMS Bookstore, ISBN 978-0-8218-4873-9, bab 5
- ^ Bateman, P.T.; Diamond, Harold G. (2004), Analytic number theory: an introductory course, New Jersey: World Scientific, ISBN 978-981-256-080-3, OCLC 492669517, teorema 4.1
- ^ P. T. Bateman & Diamond 2004, Teoerma 8.15
- ^ Slomson, Alan B. (1991), An introduction to combinatorics, London: CRC Press, ISBN 978-0-412-35370-3, bab 4
- ^ Ganguly, S. (2005), Elements of Complex Analysis, Kolkata: Academic Publishers, ISBN 978-81-87504-86-3, Definisi 1.6.3
- ^ Nevanlinna, Rolf Herman; Paatero, Veikko (2007), "Introduction to complex analysis", London: Hilger, Providence, RI: AMS Bookstore, Bibcode:1974aitc.book.....W, ISBN 978-0-8218-4399-4, bagian 5.9
- ^ Moore, Theral Orvis; Hadlock, Edwin H. (1991), Complex analysis, Singapore: World Scientific, ISBN 978-981-02-0246-0, bagian 1.2
- ^ Wilde, Ivan Francis (2006), Lecture notes on complex analysis, London: Imperial College Press, ISBN 978-1-86094-642-4, teorema 6.1.
- ^ Higham, Nicholas (2008), Functions of Matrices. Theory and Computation, Philadelphia, PA: SIAM, ISBN 978-0-89871-646-7, bab 11.
- ^ Neukirch, Jürgen (1999), Algebraische Zahlentheorie, Grundlehren der mathematischen Wissenschaften, 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, MR 1697859, Zbl 0956.11021, bagian II.5.
- ^ Hancock, Edwin R.; Martin, Ralph R.; Sabin, Malcolm A. (2009), Mathematics of Surfaces XIII: 13th IMA International Conference York, UK, September 7–9, 2009 Proceedings, Springer, hlm. 379, ISBN 978-3-642-03595-1
- ^ Stinson, Douglas Robert (2006), Cryptography: Theory and Practice (edisi ke-3rd), London: CRC Press, ISBN 978-1-58488-508-5
- ^ Lidl, Rudolf; Niederreiter, Harald (1997), Finite fields
 , Cambridge University Press, ISBN 978-0-521-39231-0
, Cambridge University Press, ISBN 978-0-521-39231-0
- ^ Corless, R.; Gonnet, G.; Hare, D.; Jeffrey, D.; Knuth, Donald (1996), "On the Lambert W function" (PDF), Advances in Computational Mathematics, 5: 329–59, doi:10.1007/BF02124750, ISSN 1019-7168, diarsipkan dari versi asli (PDF) tanggal 14 Desember 2010, diakses tanggal 13 Februari 2011
- ^ Cherkassky, Vladimir; Cherkassky, Vladimir S.; Mulier, Filip (2007), Learning from data: concepts, theory, and methods, Wiley series on adaptive and learning systems for signal processing, communications, and control, New York: John Wiley & Sons, ISBN 978-0-471-68182-3, hlm. 357
- ^ Bourbaki, Nicolas (1998), General topology. Chapters 5–10, Elements of Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64563-4, MR 1726872, bagian V.4.1
- ^ Ambartzumian, R.V. (1990), Factorization calculus and geometric probability
 , Cambridge University Press, ISBN 978-0-521-34535-4, bagian 1.4
, Cambridge University Press, ISBN 978-0-521-34535-4, bagian 1.4
- ^ Esnault, Hélène; Viehweg, Eckart (1992), Lectures on vanishing theorems, DMV Seminar, 20, Basel, Boston: Birkhäuser Verlag, CiteSeerX 10.1.1.178.3227
 , doi:10.1007/978-3-0348-8600-0, ISBN 978-3-7643-2822-1, MR 1193913, bagian 2
, doi:10.1007/978-3-0348-8600-0, ISBN 978-3-7643-2822-1, MR 1193913, bagian 2
- ^ Apostol, T.M. (2010), "Logaritma", dalam Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
Pranala luar
[sunting | sunting sumber] Media tentang Logarithm di Wikimedia Commons
Media tentang Logarithm di Wikimedia Commons Definisi kamus logaritma di Wikikamus
Definisi kamus logaritma di Wikikamus A lesson on logarithms can be found on Wikiversity
A lesson on logarithms can be found on Wikiversity- (Inggris) Weisstein, Eric W., "Logarithm", MathWorld
- Khan Academy: Logarithms, free online micro lectures
- Hazewinkel, Michiel, ed. (2001) [1994], "Logarithmic function", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
- Colin Byfleet, Educational video on logarithms, diakses tanggal 12 October 2010
- Edward Wright, Translation of Napier's work on logarithms, diarsipkan dari versi asli tanggal 3 December 2002, diakses tanggal 12 October 2010
 Glaisher, James Whitbread Lee (1911), "Logarithm", dalam Chisholm, Hugh, Encyclopædia Britannica, 16 (edisi ke-11), Cambridge University Press, hlm. 868–77
Glaisher, James Whitbread Lee (1911), "Logarithm", dalam Chisholm, Hugh, Encyclopædia Britannica, 16 (edisi ke-11), Cambridge University Press, hlm. 868–77











![{\displaystyle \scriptstyle {\sqrt[{\text{pangkat}}]{\scriptstyle {\text{radikan}}}}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b19418be0cf9ed355df169ae0dc3df1084139542)














![{\textstyle ^{b}\!\log {\sqrt[{p}]{x}}={\frac {^{b}\!\log x}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0c1e18a9c48fb08b3dbbf2387e0646fefcc3303)



















![{\displaystyle {\sqrt[{d}]{c}}=c^{\frac {1}{d}}=10^{{\frac {1}{d}}\,^{10}\!\log c}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e30502b2965ed055a829e5a3eddbcb4afb79ef8d)
































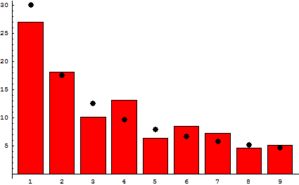

![{\displaystyle {\frac {466}{440}}\approx {\frac {493}{466}}\approx 1,059\approx {\sqrt[{12}]{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4a4571d8dc6ff40e6042496a3a6393c6d4a8b99)



![{\displaystyle {\begin{aligned}2^{\frac {4}{12}}&={\sqrt[{3}]{2}}\\&\approx 1.2599\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76610ca7878ea438fa73bd50ac4df1fecce09b9f)


![{\displaystyle ^{\sqrt[{12}]{2}}\!\log r=12\,^{2}\!\log r}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbbff697ad50b2a11b9dd950a993569e9fbd687e)






![{\displaystyle ^{\sqrt[{1200}]{2}}\!\log r=1200\,^{2}\!\log r}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82119fb5a559f76705c1639cb63b2fb210e081a4)
















