Pengguna:Klasüo/bak pasir/Arsip 31

"Eksponen" beralih ke halaman ini. Untuk kegunaan lain, lihat Eksponen (disambiguasi).

Grafik y = b^x untuk sebagai basis b:   basis 10,   basis e,   basis 2,   basis 12. Setiap kurva melewati titik (0, 1) karena setiap bilangan bukan nol kuasa 0 adalah 1. Pada x = 1, nilai y sama dengan basis karena setiap bilangan yang dipangkatkan 1 adalah bilangan itu sendiri.

Templat:Hasil perhitungan

Eksponensial adalah matematika operasi, ditulis sebagai bⁿ, melibatkan dua angka, basis b dan eksponen atau kuasa n, dan diucapkan sebagai "b sebagai kuasa n". Ketika n adalah bilangan bulat positif, eksponensial sesuai dengan perkalian berulang dari basis: yaitu, bⁿ adalah darab dari perkalian n basis:

$b^{n}=\underbrace {b\times \dots \times b} _{n{\text{ kali}}}.$

Eksponen biasanya ditampilkan sebagai superskrip sebelah kanan basis. Dalam hal ini, bⁿ disebut "b kuasa ke n", "b kuasa n", "kuasa n dari b", "b ke kuasa n", atau disingkat sebagai "b ke n".

Satu memiliki b¹ = b, dan, untuk sembarang bilangan bulat positif m dan n, apabila memiliki bⁿ ⋅ b^m = b^n+m. Untuk memperluas properti ini ke eksponen bilangan bulat non-positif, b⁰ didefinisikan sebagai 1, dan b⁻ⁿ (dengan n bilangan bulat positif dan b bukan nol) didefinisikan sebagai 1bⁿ. Khususnya, b⁻¹ sama dengan 1b, timbal balik dari b.

Definisi eksponensial diperluas untuk memungkinkan eksponen real atau kompleks. Eksponen dengan eksponen bilangan bulat juga dapat didefinisikan untuk berbagai macam struktur aljabar, termasuk matriks.

Eksponen digunakan secara luas di banyak bidang, termasuk ekonomi, biologi, kimia, fisika, dan ilmu komputer, dengan aplikasi seperti bunga majemuk, pertumbuhan populasi, kinetika reaksi kimia, perilaku gelombang, dan kriptografi kunci publik.

Sejarah notasi

Istilah kuasa (bahasa Latin: potentia, potestas, dignitas) adalah terjemahan yang salah dari Yunani kuno (dúnamis, "amplifikasi") yang digunakan oleh matematikawan Yunani Euklides untuk garis kuadrat, mengikuti Hippocrates dari Chios. Dalam The Sand Reckoner, Archimedes menemukan dan membuktikan hukum eksponen, 10^a ⋅ 10^b = 10^a+b, diperlukan untuk memanipulasi kuasa 10. Pada abad ke-9, matematikawan Persia Muhammad ibn Mūsā al-Khwārizmī menggunakan istilah ال (māl, "harta", "properti") untuk persegi— kaum muslimin, "seperti kebanyakan matematikawan pada masa itu dan sebelumnya, menganggap bilangan kuadrat sebagai penggambaran suatu area, terutama tanah, bahkan properti"—dan كَعْبَة (kaʿbah, "kubus") untuk kubus, yang kemudian matematikawan Islam diwakili dalam notasi matematika sebagai huruf mīm (m) dan kāf (k), masing-masing, pada abad ke-15, seperti yang terlihat dalam karya Abū al-Hasan ibn Alī al-Qalasādī.

Pada akhir abad ke-16, Jost Bürgi menggunakan bilangan Romawi untuk eksponen.

Nicolas Chuquet menggunakan bentuk notasi eksponensial pada abad ke-15, yang kemudian digunakan oleh Henricus Grammateus dan Michael Stifel pada abad ke-16. Kata "eksponen" diciptakan pada tahun 1544 oleh Michael Stifel. Samuel Jeake memperkenalkan istilah indeks pada tahun 1696. Pada abad ke-16, Robert Recorde menggunakan istilah persegi, kubus, zenzizenzic (kuasa keempat), padatan (kelima), kubuszenzi (keenam), padatan kedua (ketujuh), dan zenzizenzizenzik (kedelapan). Biquadrate telah digunakan untuk merujuk pada kuasa keempat juga.

Pada awal abad ke-17, bentuk pertama dari notasi eksponensial modern diperkenalkan oleh René Descartes dalam teksnya yang berjudul La Géométrie; terdapat, notasi diperkenalkan di Buku I.

Beberapa matematikawan (seperti Isaac Newton) menggunakan eksponen hanya untuk pangkat yang lebih besar dari dua, lebih memilih untuk merepresentasikan kuadrat sebagai perkalian berulang. Jadi ketika akan menulis polinomial, misalnya, sebagai ax + bxx + cx³ + d.

Sinonim sejarah lainnya dalam penggunaan involusi, dan jangan bingung dengan artinya yang lebih umum.

Pada tahun 1748, Leonhard Euler memperkenalkan eksponen variabel, dan, secara implisit, eksponen non-bilangan bulat dengan menulis:

"pertimbangkan eksponensial atau kuasa dimana eksponen itu sendiri adalah variabel. Jelaskan besaran-besaran seperti ini bukanlah fungsi aljabar, karena eksponennya harus konstan."

Terminologi

Ekspresi b² = b b disebut "persegi dari b" atau "b kuadrat", karena luas persegi dengan panjang sisi b adalah b².

Demikian pula, ekspresi b³ = b b b disebut "kubus dari b" atau "b pangkat tiga", karena volume kubus dengan panjang rusuk b adalah b³.

Ketika itu adalah bilangan bulat positif, eksponen menunjukkan berapa banyak salinan dari basis yang dikalikan bersama. Misalnya, 3⁵ = 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 243. Basis 3 muncul 5 kali dalam perkalian, karena eksponennya adalah 5. Maka, 243 adalah kuasa ke-5 dari 3, atau 3 terkuasa ke-5.

Kata "terkuasa" biasanya dihilangkan, dan terkadang "kuasa" juga, jadi 3⁵ dapat dibaca "3 ke 5", atau "3 ke 5 ". Oleh karena itu, eksponensial bⁿ dinyatakan sebagai "b untuk kuasa n", "b untuk kuasa ke-n", "b untuk ke-n", atau disingkat juga sebagai "b untuk n ".

Rumus dengan eksponensial bertingkat, seperti 3⁵⁷ (yang berarti 3⁽⁵⁷⁾ dan bukan (3⁵)^{7</ sup>}), disebut juga sebagai menara kuasa', atau hanya menara.

Eksponen bilangan bulat

Operasi eksponensial dengan eksponen bilangan bulat didefinisikan langsung dari operasi aritmetika dasar.

Eksponen positif

Definisi eksponensial sebagai perkalian teriterasi dibuktikan secara formalisasi dengan menggunakan induksi, dan definisi ini digunakan segera apabila memiliki perkalian asosiasi:

Kasus dasarnya adalah

$b^{1}=b$

dan pengulangan adalah

$b^{n+1}=b^{n}\cdot b.$

Asosiasi perkalian menyatakan bahwa untuk sembarang bilangan bulat positif m dan n, adalah

$b^{m+n}=b^{m}\cdot b^{n},$

dan

$(b^{m})^{n}=b^{mn}.$

Eksponen nol

Menurut definisi, setiap bilangan bukan nol yang terkuasa ke kuasa 0 adalah 1:

$b^{0}=1.$

Definisi ini adalah satu-satunya kemungkinan yang memungkinkan perluasan rumus

$b^{m+n}=b^{m}\cdot b^{n}$

ke nol eksponen. Ini digunakan pada setiap struktur aljabar dengan perkalian yang memiliki identitas.

Secara intuitif, $b^{0}$ diartikan sebagai darab kosong dari salinan b. Jadi, persamaan $b^{0}=1$ adalah kasus khusus dari konvensi umum untuk darab kosong.

Kasus 0⁰ adalah lebih rumit. Dalam konteks dimana kuasa bilangan bulat yang dipertimbangkan, nilai 0 umumnya ditetapkan ke $0^{0},$ namun, jika tidak, pilihan apakah akan menetapkan nilai dan nilai apa yang akan ditetapkan mungkin bergantung pada konteks.

Untuk detail selengkapnya, lihat Nol ke kuasa nol.

Eksponen negatif

Eksponen dengan eksponen negatif didefinisikan oleh identitas berikut, yang berlaku untuk sembarang bilangan bulat n dan bukan nol b:

$b^{-n}={\frac {1}{b^{n}}}.$

Menaikkan 0 ke eksponen negatif tidak ditentukan, tetapi dalam beberapa keadaan, apabila ditafsirkan sebagai tak hingga ($\infty$).

Definisi eksponen dengan eksponen negatif ini adalah satu-satunya yang memungkinkan perluasan identitas $b^{m+n}=b^{m}\cdot b^{n}$ ke eksponen negatif (pertimbangkan kasus $m=-n$).

Definisi yang sama berlaku untuk elemen terbalikkan dalam monoid perkalian, yaitu, struktur aljabar dengan perkalian asosiatif dan identitas perkalian yang dilambangkan 1 (misalnya, matriks persegi dari dimensi tertentu). Secara khusus, dalam struktur ini, invers dari elemen terbalikkan x secara standar dilambangkan sebagai $x^{-1}.$

Identitas dan sifat

"Hukum Indeks" beralih ke halaman ini. Untuk kuda, lihat Hukum Indeks (kuda).

Identitas berikut ini, sering disebut sebagai kaidah eksponen, untuk semua eksponen bilangan bulat, asalkan basisnya bukan nol:

${\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\\left(b^{m}\right)^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}$

Tidak seperti penjumlahan dan perkalian, eksponensial bukanlah komutatif. Misalnya, 2³ = 8 ≠ 3² = 9. Juga tidak seperti penjumlahan dan perkalian, eksponensial tidak asosiatif. Misalnya, (2³)² = 8² = 64, dimana 2⁽³²⁾ = 2⁹ = 512. Tanpa tanda kurung, urutan operasi konvensional untuk deret eksponensial dalam notasi superskrip adalah top-down (atau asosiatif-kanan), bukan bottom-up (atau asosiatif-kiri). Maka,

$b^{p^{q}}=b^{\left(p^{q}\right)},$

yang secara umum berbeda dengan

$\left(b^{p}\right)^{q}=b^{pq}.$

Kuasa jumlah

Kuasa jumlah biasanya dihitung dari kuasa penjumlahan dengan rumus binomial

$(a+b)^{n}=\sum _{i=0}^{n}{\binom {n}{i}}a^{i}b^{n-i}=\sum _{i=0}^{n}{\frac {n!}{i!(n-i)!}}a^{i}b^{n-i}.$

Namun, rumus ini hanya berlaku jika jumlah komuter (yaitu ab = ba), yang menyatakan apabila ia termasuk dalam struktur yaitu komutatif. Jika tidak, a dan b adalah matriks persegi dengan ukuran yang sama, rumus ini tidak dapat digunakan. Oleh karena itu dalam aljabar komputer, banyak algoritma yang melibatkan eksponen bilangan bulat diubah ketika basis eksponensial tidak komuter. Beberapa tujuan umum sistem aljabar komputer menggunakan notasi yang berbeda (terkadang, ^^ sebagai gantinya adalah ^) untuk eksponensial dengan basis non-komuter, yang kemudian disebut eksponensial non-komutatif.

Interpretasi kombinatorial

Lihat pula: Eksponen atas himpunan

Untuk bilangan bulat tak negatif n dan m, nilai dari n^m adalah jumlah fungsi dari himpunan elemen m ke himpunan elemen n (lihat eksponensial kardinal). Fungsi tersebut direpresentasikan sebagai rangkap-m dari elemen himpunan-n (atau sebagai kata huruf m dari alfabet huruf n). Beberapa contoh untuk nilai m dan n tertentu diberikan dalam tabel berikut:

nm	nm kemungkinan rangkap-m elemen dari himpunan (1, ..., n}
05 = 0	tidak ada
14 = 1	(1, 1, 1, 1)
23 = 8	(1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2)
32 = 9	(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)
41 = 4	(1), (2), (3), (4)
50 = 1	()

Basis tertentu

Kuasa sepuluh

Lihat pula: Notasi ilmiah

Artikel utama: Kuasa 10

Dalam sistem bilangan basis sepuluh (desimal), kuasa bilangan bulat 10 ditulis sebagai digit 1 diikuti atau didahului oleh sejumlah nol yang ditentukan oleh tanda dan besaran eksponen. Misalnya, 10³ = 1000 dan 10⁻⁴ = 00.001.

Eksponen dengan basis 10 digunakan dalam notasi ilmiah untuk menyatakan bilangan besar atau kecil. Misalnya, 299.792.458 m/s (kecepatan cahaya dalam ruang hampa), dalam meter per detik) dapat ditulis sebagai 299.792.458×10⁸ m/s dan kemudian perkiraan sebagai 2998×10⁸ m/s.

Awalan SI berdasarkan kuasa 10 yang juga digunakan untuk menggambarkan jumlah kecil atau besar. Misalnya, awalan kilo berarti 10³ = 1000, jadi satu kilometer adalah 1000 m.

Kuasa dua

Artikel utama: Kuasa dua

Pangkat negatif pertama 2 biasanya digunakan, dan memiliki nama khusus, misalnya: setengah dan kuarterner.

Kuasa 2 muncul di teori himpunan, karena himpunan dengan anggota n memiliki himpunan kuasa, himpunan semua himpunan bagian-nya, yang memiliki anggota 2ⁿ.

Kuasa bilangan bulat 2 penting dalam ilmu komputer. Bilangan bulat positif kuasa 2ⁿ memberikan jumlah bilangan yang mungkin untuk bitn bilangan bulat bilangan biner; misalnya, bita dapat mengambil 2⁸ = 256 nilai yang berbeda. Sistem bilangan biner menyatakan bilangan sebagai jumlah dari kuasa 2, dan menyatakannya sebagai urutan 0 dan 1, dipisahkan oleh titik biner, dimana 1 menunjukkan kuasa 2 yang muncul dalam penjumlahan; eksponen ditentukan oleh tempat 1 ini: eksponen nonnegatif adalah kuasa 1 sebelah kiri titik (mulai dari 0), dan eksponen negatif ditentukan oleh peringkat sebelah kanan titik.

Kuasa satu

Kuasa satu adalah semua satu: 1ⁿ = 1.

Kuasa nol

Jika eksponen n positif (n > 0), kuasa ke-n dari nol adalah nol: 0ⁿ = 0.

Jika eksponen n negatif (n < 0), kuasa ke-n dari nol 0 ⁿ tidak ditentukan, karena itu harus sama dengan $1/0^{-n}$ dengan −n > 0, dan ini sebagai menjadi $1/0$.

Ekspresi 0⁰ didefinisikan sebagai 1, atau maka tidak terdefinisi (lihat Nol untuk kuasa nol).

Kuasa negatif satu

Jika n adalah bilangan bulat genap, maka (−1)ⁿ = 1.

Jika n adalah bilangan bulat ganjil, maka (−1)ⁿ = −1.

Oleh karena itu, kuasa −1 berguna untuk menyatakan sebagai urutan bergantian. Untuk diskusi serupa tentang kuasa bilangan kompleks i, lihat § Kuasa bilangan kompleks.

Eksponen besar

Limit barisan kuasa dari bilangan besar dari satu divergen; dengan kata lain, barisan tersebut terikat tanpa batas:

bⁿ → ∞ sebagai n → ∞ jika b > 1

Apabila dibaca sebagai "b kuasa n cenderung +∞ sebagai n cenderung tak hingga ketika b memiliki nilai besar daripada satu".

Kuasa suatu bilangan dengan nilai absolut kurang dari satu cenderung nol:

bⁿ → 0 sebagai n → ∞ jika |b| < 1

Setiap kuasa satu tetap satu:

bⁿ = 1 untuk semua n jika b = 1

Kuasa –1 berganti antara 1 dan –1 sebagai n berganti antara genap dan ganjil, dan dengan demikian tidak cenderung ke limit apabila sebagai pertumbuhan n.

Jika b < –1, bⁿ, berganti sebagai bilangan positif dan negatif besar dan n berganti sebagai genap dan ganjil, dan dengan demikian tidak cenderung ke limit apabila sebagai pertumbuhan n.

Jika bilangan eksponen berubah cenderung ke 1 karena eksponen cenderung tak hingga, maka limitnya belum tentu salah satu atas. Kasus yang sangat penting adalah

(1 + 1/n)ⁿ → e sebagai n → ∞

Lihat § Fungsi eksponensial dibawah ini.

Limit lain, khususnya ekspresi yang menggunakan bentuk antara, dijelaskan dalam § Kuasa limit dibawah.

Fungsi kuasa

Fungsi kuasa untuk $n=1,3,5$

Fungsi kuasa untuk $n=2,4,6$

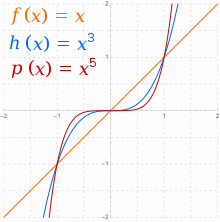
Fungsi real dari bentuk $f(x)=cx^{n}$, dimana $c\neq 0$, terkadang disebut sebagai fungsi pangkat. Ketika $n$ adalah bilangan bulat dan $n\geq 1$, maka terdapat dua keluarga keujudan, yaitu: untuk $n$ genap, dan untuk $n$ ganjil. Secara umum untuk $c>0$, bila $n$ genap $f(x)=cx^{n}$ cenderung ke arah positif ketakterhinggaan dengan penambahan $x$, dan juga menuju tak hingga positif dengan turunan $x$. Semua grafik dari keluarga fungsi pangkat genap memiliki bentuk umum $y=cx^{2}$, yang merata ditengah sebagai tingkatan $n$. Fungsi dengan simetri ($f(-x)=f(x)$) seperti ini disebut fungsi genap.

Ketika $n$ ganjil, perilaku asimptotik $f(x)$ berbalik dari $x$ positif ke $x$ negatif. Untuk $c>0$, $f(x)=cx^{n}$ juga cenderung ke arah positif ketakterhinggaan dengan tingkatan $x$, tetapi menuju ketakterhinggaan negatif dengan turunan $x$. Semua grafik dari keluarga fungsi kuasa ganjil memiliki bentuk umum $y=cx^{3}$, merata ditengah ketika tingkatan $n$ dan kehilangan semua kerataan di garis lurus untuk $n=1$. Fungsi dengan simetri seperti ini ($f(-x)=-f(x)$) disebut fungsi ganjil.

Untuk $c<0$, perilaku asimtotik berlawanan berlaku untuk setiap kasus.

Daftar kuasa bilangan bulat

n	n2	n3	n4	n5	n6	n7	n8	n9	n10
2	4	8	16	32	64	128	256	512	1024
3	9	27	81	243	729	2187	6561	19.683	59.049
4	16	64	256	1024	4096	16.384	65.536	262.144	1.048.576
5	25	125	625	3125	15.625	78.125	390.625	1.953.125	9.765.625
6	36	216	1296	7776	46.656	279.936	1.679.616	10.077.696	60.466.176
7	49	343	2401	16.807	117.649	823.543	5.764.801	40.353.607	282.475.249
8	64	512	4096	32.768	262.144	2.097.152	16.777.216	134.217.728	1.073.741.824
9	81	729	6561	59.049	531.441	4.782.969	43.046.721	387.420.489	3.486.784.401
10	100	1000	10.000	100.000	1.000.000	10.000.000	100.000.000	1.000.000.000	10.000.000.000

Eksponen rasional

Dari atas ke bawah: x^1/8, x^1/4, x^1/2, x¹, x², x⁴, x⁸.

Jika x adalah bilangan real nonnegatif, dan n adalah bilangan bulat positif, $x^{\frac {1}{n}}$ atau ${\sqrt[{n}]{x}}$ menunjukkan real positif unik akar ke-n dari x, yaitu, bilangan real positif unik y sehingga $y^{n}=x.$

Jika x adalah bilangan real positif, dan ${\frac {p}{q}}$ adalah bilangan rasional, dengan p dan q ≠ 0 bilangan bulat, maka ${\textstyle x^{\frac {p}{q}}}$ didefinisikan sebagai

$x^{\frac {p}{q}}=\left(x^{p}\right)^{\frac {1}{q}}=(x^{\frac {1}{q}})^{p}.$

Persamaan sebelah kanan diturunkan dengan menetapkan $y=x^{\frac {1}{q}},$ dan menulis $(x^{\frac {1}{q}})^{p}=y^{p}=\left((y^{p})^{q}\right)^{\frac {1}{q}}=\left((y^{q})^{p}\right)^{\frac {1}{q}}=(x^{p})^{\frac {1}{q}}.$

Jika r adalah bilangan rasional positif, $0^{r}=0,$ menurut definisi.

Semua definisi ini diperlukan untuk memperluas identitas $(x^{r})^{s}$ ke eksponen rasional.

Di sisi lain, ada masalah dengan perluasan definisi ini ke basis yang bukan bilangan real positif. Misalnya, bilangan real negatif memiliki akar ke-n real, yang negatif jika n adalah ganjil, dan tidak memiliki akar real jika n genap. Dalam kasus terakhir, kompleks mana pun akar ke-n memilih satu untuk $x^{\frac {1}{n}},$ identitas $(x^{a})^{b}=x^{ab}$. Misalnya,

$\left((-1)^{2}\right)^{\frac {1}{2}}=1^{\frac {1}{2}}=1\neq (-1)^{2\cdot {\frac {1}{2}}}=(-1)^{1}=-1.$

Lihat § Eksponen real dengan basis negatif dan § Kuasa bilangan kompleks untuk detail tentang cara menangani masalah ini.

Eksponen real

Untuk bilangan real positif, eksponensial untuk kuasa real dapat didefinisikan dalam dua cara yang setara, baik dengan memperluas kuasa rasional ke real dengan kontinuitas (§ Limit eksponen rasional, dibawah), atau dalam hal logaritma dari basis dan fungsi eksponensial (§ Kuasa melalui logaritma, dibawah). Hasilnya bilangan real positif, dan identitas dan sifat yang ditunjukkan atas untuk eksponen bilangan bulat tetap benar dengan definisi ini untuk eksponen real. Definisi kedua lebih umum digunakan, karena digeneralisasikan secara langsung ke kompleks eksponen.

Di sisi lain, eksponensial ke kuasa real dari bilangan real negatif jauh lebih sulit untuk didefinisikan secara konsisten, karena mungkin non-real dan memiliki beberapa nilai (lihat § Eksponen real dengan basis negatif). Apabila memilih salah satu dari nilai-nilai ini, yang disebut nilai utama, tetapi tidak ada pilihan nilai utama yang identitasnya

$\left(b^{r}\right)^{s}=b^{rs}$

adalah benar; lihat § Kegagalan kuasa dan identitas logaritma. Oleh karena itu, eksponensial dengan basis yang bukan bilangan real positif umumnya dipandang sebagai fungsi multinilai.

Limit eksponen rasional

Limit e^1/n adalah e⁰ = 1 ketika n cenderung ketakterhinggaan.

Karena bilangan irasional dapat dinyatakan sebagai limit barisan dari bilangan rasional, eksponen bilangan real positif b dengan eksponen real arbitrer x didefinisikan oleh kontinuitas dengan kaidah

$b^{x}=\lim _{r(\in \mathbb {Q} )\to x}b^{r}\quad (b\in \mathbb {R} ^{+},\,x\in \mathbb {R} ),$

dimana limitnya diambil alih nilai rasional r saja. Limit ini ada untuk setiap b positif dan setiap x real.

Misalnya, jika x = π, diwakilankan desimal tanpa π = 3.14159... dan monotonisitas dari kuasa rasional digunakan untuk mendapatkan interval dibatasi oleh kuasa rasional sekecil yang diinginkan, dan dilambangkan sebagai $b^{\pi }:$

$\left[b^{3},b^{4}\right],\left[b^{3.1},b^{3.2}\right],\left[b^{3.14},b^{3.15}\right],\left[b^{3.141},b^{3.142}\right],\left[b^{3.1415},b^{3.1416}\right],\left[b^{3.14159},b^{3.14160}\right],\ldots$

Jadi, batas atas dan batas bawah interval membentuk dua barisan yang memiliki limit yang sama, dilambangkan dengan sebagai $b^{\pi }.$

Apabila mendefinisikan $b^{x}$ untuk setiap b positif dan x positif sebagai fungsi kontinu dari b dan x.

Fungsi eksponensial

Artikel utama: Fungsi eksponensial

Fungsi eksponensial didefinisikan sebagai $x\mapsto e^{x},$ dimana $e\approx 2,718$ adalah bilangan Euler. Untuk menghindari penalaran lingkar, definisi ini tidak dapat digunakan di sini. Jadi, diberikan definisi fungsi eksponensial, dinotasikan $\exp(x),$ dan dari bilangan Euler bebas dari eksponensial. Kemudian sebuah bukti dibuat sketsa, bahwa apabila jika menggunakan definisi eksponensial yang diberikan pada bagian sebelumnya, maka memiliki:

$\exp(x)=e^{x}.$

Terdapat banyak cara ekuivalen untuk mendefinisikan fungsi eksponensial, salah satunya adalah mendefinisikannya sebagai fungsi invers dari logaritma alami. Tepatnya, logaritma natural adalah antiturunan dari $1/x$ yang mengambil nilai 0 untuk x = 1 :

$\ln x=\int _{1}^{x}{\frac {dt}{t}}.$

Apabila mendefinisikan logaritma sebagai fungsi meningkat dari real positif ke bilangan real. Fungsi invers dan fungsi eksponensial dengan demikian merupakan fungsi naik dari bilangan real ke real positif, yang biasa dilambangkan exp. Satu satunya, memiliki

$\exp(0)=1,$

dan identitas eksponensial

$\exp(x+y)=\exp(x)\exp(y)$

untuk setiap x dan y.

Bilangan Euler didefinisikan sebagai $e=\exp(1)$. Maka, ini mengikuti dari persamaan sebelumnya bahwa $\exp(x)=e^{x}$ dengan x adalah bilangan bulat (ini hasil dari definisi perkalian berulang dari eksponensial). Jika x adalah real, $\exp(x)=e^{x}$ dihasilkan dari definisi yang diberikan pada bagian sebelumnya, dengan menggunakan identitas eksponensial jika x adalah rasional, dan kontinuitas fungsi eksponensial sebaliknya.

Fungsi eksponensial memenuhi persamaan

$\exp(x)=\sum _{n=0}^{\infty }{\frac {x^{n}}{n}}.$

Karena deret konvergen untuk setiap kompleks nilai x dengan persamaan yang memungkinkan pendefinisian fungsi eksponensial, dan demikian pula $e^{z},$ untuk argumen kompleks z. Fungsi eksponensial diperluas masih memenuhi identitas eksponensial, dan biasanya digunakan untuk mendefinisikan eksponensial untuk basis kompleks dan eksponen.

Kuasa melalui logaritma

Definisi e^x sebagai fungsi eksponensial didefinisikan b^x untuk setiap bilangan real positif b, dalam hal fungsi eksponensial dan logaritmik. Secara khusus, bahwa logaritma natural ln(x) adalah invers dari fungsi eksponensial e ^x maka ia memiliki

$b=\exp(\ln b)=e^{\ln b}$

untuk setiap b > 0. Untuk mempertahankan identitas $(e^{x})^{y}=e^{xy},$ maka ia memiliki

$b^{x}=\left(e^{\ln b}\right)^{x}=e^{x\ln b}$

Jadi, $e^{x\ln b}$ digunakan sebagai definisi alternatif dari b^x untuk setiap real positif b. Ini sesuai dengan definisi yang diberikan di atas menggunakan eksponen rasional dan kontinuitas, dengan memperluas secara langsung ke eksponen kompleks mana pun.

Eksponen kompleks dengan basis real positif

Jika b adalah bilangan real positif, eksponen dengan basis b dan kompleks eksponen didefinisikan melalui fungsi eksponensial dengan argumen kompleks (lihat dibagian akhir § Fungsi eksponensial, diatas) sebagai

$b^{z}=e^{(z\ln b)},$

dimana $\ln b$ menunjukkan logaritma natural dari b.

Maka, ini memenuhi identitas

$b^{z+t}=b^{z}b^{t},$

Secara umum, ${\textstyle \left(b^{z}\right)^{t}}$ tidak didefinisikan, karena b^z bukan bilangan real. Jika suatu arti diberikan pada eksponen bilangan kompleks (lihat § Kuasa bilangan kompleks, dibawah), secara umum,

$\left(b^{z}\right)^{t}\neq b^{zt},$

kecuali z adalah real atau w adalah bilangan bulat.

Rumus Euler $e^{iy}=\cos y+i\sin y,$ mengekspresikan bentuk polar dari $b^{z}$ dalam hal bagian real dan imajiner dari z, yaitu

$b^{x+iy}=b^{x}(\cos(y\ln b)+i\sin(y\ln b)),$

dimana nilai absolut dari faktor trigonometri adalah satu. Maka, hasilnya adalah

$b^{x+iy}=b^{x}b^{iy}=b^{x}e^{iy\ln b}=b^{x}(\cos(y\ln b)+i\sin(y\ln b)).$

Kuasa bilangan kompleks non-bilangan bulat

Pada bagian sebelumnya, eksponen dengan eksponen non-bilangan bulat telah didefinisikan hanya untuk basis real positif. Untuk basis lain, kesulitan muncul dengan kasus sederhana dari akar ke-n, yaitu, dari eksponen $1/n,$ dimana n adalah bilangan bulat positif. Meskipun teori umum eksponensial dengan eksponen bukan bilangan bulat yang berlaku untuk akar ke-n, kasus ini layak untuk dipertimbangkan terlebih dahulu, karena tidak perlu menggunakan logaritma kompleks, dan karena itu lebih mudah dipahami.

Akar ke-n pada bilangan kompleks

Setiap bilangan kompleks bukan nol z dapat ditulis dalam bentuk polar sebagai

$z=\rho e^{i\theta }=r(cos\theta +i\sin \theta ),$

dimana $\rho$ adalah nilai absolut dari z, dan $\theta$ adalah argumen. Argumen didefinisikan hingga bilangan bulat kelipatan 2π; ini berarti, jika $\theta$ adalah argumen dari bilangan kompleks, maka $\theta +2k\pi$ juga merupakan argumen dari bilangan kompleks yang sama.

Bentuk polar dari darab dua bilangan kompleks diperoleh dengan mengalikan nilai absolut dan menambahkan argumen. Oleh karena itu, bentuk kutub dari akar ke-n dari bilangan kompleks diperoleh dengan mengambil akar ke-n dari nilai absolut dan membagi argumennya dengan n:

$\left(\rho e^{i\theta }\right)^{\frac {1}{n}}={\sqrt[{n}]{\rho }}\,e^{\frac {i\theta }{n}}.$

Jika $2i\pi$ ditambahkan ke $\theta ,$ maka bilangan kompleks tersebut tidak berubah, tetapi ini menambahkan $2i\pi /n$ ke argumen akar ke-n, dan diberikan akar ke-n yang baru. Ini dilakukan kali n, dan diberikan kepada akar ke-n n dari bilangan kompleks.

Biasanya memilih salah satu dari akar ke-n n sebagai akar utama. Pilihan umum adalah memilih akar ke-n sebagai $-\pi <\theta \leq \pi ,$ yaitu, akar ke-n yang memiliki bagian real terbesar, dan jika keduanya adalah dua dari bagian imajiner positif tersebut. Ini membuat akar ke-n utama sebuah fungsi kontinu dalam seluruh bidang kompleks, kecuali untuk nilai real negatif dari radikan. Fungsi ini sama dengan akar ke-n biasa untuk radikan real positif. Untuk radikan real negatif, dan eksponen ganjil, akar ke-n utama bukanlah real, meskipun akar ke-n yang biasa adalah real. Kelanjutan analitik menunjukkan bahwa prinsip akar ke-n utama adalah fungsi unik diferensial kompleks yang memperluas fungsi akar ke-n medan kompleks tanpa bilangan real yang bukan positif.

Jika bilangan kompleks dipindahkan sekitar nol dengan meningkatkan argumennya, setelah kenaikan $2\pi ,$ bilangan kompleks kembali ke posisi awal, dan akar ke-n-nya adalah permutasi lingkar (yang dikalikan dengan $e^{2i\pi /n}$). Ini menunjukkan bahwa tidak mungkin untuk mendefinisikan fungsi akar ke-n yang tidak kontinu pada seluruh medan kompleks.

Akar satuan

Artikel utama: Akar satuan

Tiga akar ke-3 dari 1

Bilangan kompleks w sedemikian rupa sehingga wⁿ = 1 untuk bilangan bulat positif n adalah akar satuan ke-n. Secara geometris, akar satuan ke-n terletak pada lingkaran satuan dari medan kompleks pada simpul-simpul dari gon-n beraturan dengan satu simpul pada bilangan real 1.

Jika wⁿ = 1 akan tetapi w^k 1 untuk semua bilangan asli k sehingga 0 < k < n, maka w disebut akar satuan ke-n primitif. Satuan negatif −1 adalah satu-satunya akar kuadrat primitif dari satuan. satuan imajiner i adalah salah satu dari dua akar ke-4 primitif dari satuan; yang lainnya adalah −i.

Bilangan e^2πin adalah akar satuan n primitif dengan argumen positif terkecil. Hal ini terkadang disebut akar kesatuan ke-n utama, meskipun terminologi ini tidaklah universal dan tidak boleh disamakan dengan nilai utama dari ⁿ√1, yaitu 1.) Akar satuan ke-n yang lain dinyatakan sebagai bentuk akar ke-n utama, yaitu $$\left(e^{\frac {2\pi i}{n}}\right)^{k}=e^{{\frac {2\pi i}{n}}k}$$ untuk 2 ≤ k ≤ n.

Eksponensial kompleks

Mendefinisikan eksponensial dengan basis kompleks menyebabkan kesulitan serupa dengan yang dijelaskan pada bagian sebelumnya, kecuali, bahwa, secara umum, ada banyak kemungkinan nilai untuk $z^{w}$. Jadi, salah satu nilai utama didefinisikan yang bukan kontinu untuk nilai z real dan nonpositif, atau $z^{w}$ didefinisikan sebagai fungsi multinilai.

Dalam semua kasus, logaritma kompleks digunakan untuk mendefinisikan eksponensial kompleks, sebagai

$z^{w}=e^{w\log z},$

dimana $\log z$ adalah varian dari logaritma kompleks yang digunakan, yaitu, fungsi atau fungsi multinilai sedemikian rupa sehingga

$e^{\log z}=z$

untuk setiap z dalam ranah definisi.

Nilai utama

Nilai utama dari logaritma kompleks adalah fungsi unik, biasanya dilambangkan $\log ,$ sehingga, untuk setiap bilangan kompleks bukan nol z,

$e^{\log z}=z,$

dan bagian imajiner dari z memenuhi

$-\pi <\mathrm {Im} \leq \pi .$

Nilai utama dari logaritma kompleks tidak didefinisikan untuk $z=0,$ hal itu disebut juga sebagai tidak kontinu pada nilai real negatif z, dan holomorfik (yaitu, terdiferensial kompleks) pada bagian lain. Jika z adalah real dan positif, nilai utama dari logaritma kompleks adalah logaritma alami: $\log z=\ln z.$

Nilai utama $z^{w}$ didefinisikan sebagai $z^{w}=e^{w\log z},$ dimana $\log z$ adalah nilai utama dari logaritma.

Fungsi $(z,w)\to z^{w}$ adalah holomorfik kecuali diantara titik-titik dimana z adalah real dan non-positif.

Jika z adalah real dan positif, nilai utama $z^{w}$ sama dengan nilai biasa yang didefinisikan di atas. Jika $w=1/n,$ dimana n adalah bilangan bulat, nilai utama ini sama dengan yang didefinisikan di atas.

Fungsi multinilai

Dalam beberapa konteks, terdapat masalah dengan diskontinuitas pada nilai-nilai utama $\log z$ dan $z^{w}$ pada nilai real negatif z. Dalam hal ini, akan berguna untuk mempertimbangkan fungsi-fungsi ini sebagai fungsi multinilai.

Jika $\log z$ menunjukkan salah satu nilai dari logaritma multinilai (biasanya nilai utamanya), nilai lainnya adalah $2ik\pi +\log z,$ dimana k adalah bilangan bulat. Demikian pula, jika $z^{w}$ adalah salah satu nilai eksponensial, maka nilai lainnya diberikan oleh

$e^{w(2ik\pi +\log z)}=z^{w}e^{2ik\pi w},$

dimana k adalah bilangan bulat.

Nilai k berbeda memberikan nilai $z^{w}$ yang berbeda kecuali w adalah bilangan rasional, yaitu, apabila bilangan bulat d sehingga dw adalah bilangan bulat. Maka hasil dari periodisitas ini dari fungsi eksponensial, bahwa $e^{a}=e^{b}$ jika dan hanya jika $a-b$ adalah kelipatan bilangan bulat dari $2\pi .$

Jika $w={\frac {m}{n}}$ adalah bilangan rasional dengan m dan n bilangan bulat koprima dengan $n>0,$ maka $z^{w}$ memiliki nilai persis n. Dalam kasus $m=1,$ nilai-nilai ini sama dengan yang dijelaskan dalam §akar ke-n bilangan kompleks. Jika w adalah bilangan bulat, maka hanya ada satu nilai yang sesuai dengan § Eksponen bilangan bulat.

Kuasa multinilai adalah holomorfik untuk $z\neq 0,$ dalam arti bahwa grafik-nya terdiri dari beberapa lembar yang mendefinisikan setiap fungsi holomorfik pada sekitar setiap titik. Jika variasi z terus menerus sepanjang lingkaran pada sekitar 0, maka, setelah titik balik, nilai $z^{w}$ berubah dari lapisan.

Komputasi

Bentuk kanonik $x+iy$ dari $z^{w}$ dihitung dari bentuk kanonik z dan w. Meskipun ini dapat dijelaskan dengan satu rumus, lebih jelas untuk membagi perhitungan dalam beberapa langkah.

• Bentuk polar dari z. Jika $z=a+ib$ adalah bentuk kanonik dari z (a dan b sebagai real), maka bentuk polar-nya adalah $$z=\rho e^{i\theta }=\rho (\cos \theta +i\sin \theta ),$$ dimana $\rho ={\sqrt {a^{2}+b^{2}}}$ dan $\theta =\operatorname {atan2} (a,b)$ (lihat atan2 untuk definisi fungsi ini).
• logaritma dari z. Nilai utama dari logaritma ini adalah $\log z=\ln \rho +i\theta ,$ dimana $\ln$ menunjukkan logaritma alami. Nilai logaritma lainnya diperoleh dengan menambahkan $2ik\pi$ untuk sembarang bilangan bulat k.
• Bentuk kanonik dari $w\log z.$ Jika $w=c+di$ dengan real c dan d, nilai $w\log z$ adalah $$w\log z=(c\ln \rho -d\theta -2dk\pi )+i(d\ln \rho +c\theta +2ck\pi ),$$ nilai utama yang sesuai dengan $k=0.$
• Hasil akhir. Menggunakan identitas $e^{x+y}e^{x}=e^{y}$ dan $e^{y\ln x}=x^{y},$ satu-satunya menggunakan $$z^{w}=\rho ^{c}e^{-d(\theta +2k\pi )}\left(\cos(d\ln \rho +c\theta +2ck\pi )+i\sin(d\ln \rho +c\theta +2ck\pi )\right),$$ dengan $k=0$ untuk nilai utama.

Contoh

• $i^{i}$
  Bentuk polar i adalah $i=e^{i\pi /2},$ dan dengan demikian nilai $\log i$ adalah $$\log i=i\left({\frac {\pi }{2}}+2k\pi \right).$$ Oleh karena itu $$i^{i}=e^{i\log i}=e^{-{\frac {\pi }{2}}}e^{-2k\pi }.$$ Jadi, semua nilai real $i^{i}$ utama adalah $$e^{-{\frac {\pi }{2}}}\approx 0.2079.$$

• $(-2)^{3+4i}$
  Similarly, bentuk polar dari −2 adalah $-2=2e^{i\pi }.$ Jadi, metode yang dijelaskan di atas diberikan nilai $${\begin{aligned}(-2)^{3+4i}&=2^{3}e^{-4(\pi +2k\pi )}(\cos(4\ln 2+3(\pi +2k\pi ))+i\sin(4\ln 2+3(\pi +2k\pi )))\\&=-2^{3}e^{-4(\pi +2k\pi )}(\cos(4\ln 2)+i\sin(4\ln 2)).\end{aligned}}$$Dalam hal ini, semua nilai memiliki argumen $4\ln 2,$ yang sama dan nilai absolut yang berbeda.

Dalam kedua contoh, semua nilai $z^{w}$ memiliki argumen yang sama. Secara umum, ini benar jika dan hanya jika bagian real dari w adalah bilangan bulat.

Kegagalan kuasa dan identitas logaritma

Beberapa identitas untuk kuasa dan logaritma untuk bilangan real positif akan gagal untuk bilangan kompleks, tidak peduli seberapa kuasa kompleks dan logaritma kompleks didefinisikan sebagai fungsi bernilai tunggal. Misalnya:

• Identitas log(b^x) = x ⋅ log b berlaku setiap b adalah bilangan real positif dan x adalah bilangan real. Tetapi untuk cabang utama dari logaritma kompleks yang dimiliki

  $i\pi =\log(-1)=\log \left[(-i)^{2}\right]\neq 2\log(-i)=2\left(-{\frac {i\pi }{2}}\right)=-i\pi$

  Terlepas dari cabang logaritma mana yang digunakan, kegagalan identitas yang serupa akan tetap ada. Yang terbaik yang bisa dikatakan (jika hanya menggunakan hasil ini) adalah bahwa:

  $\log(w^{z})\equiv z\cdot \log(w){\pmod {2\pi i}}$

  Identitas ini tidak berlaku bahkan ketika mempertimbangkan log sebagai fungsi multinilai. Nilai yang mungkin menggunakan log(w^z) berisi z log w sebagai himpunan bagian. Menggunakan Log(w) untuk nilai utama log(w) dan m, n sebagai bilangan bulat, nilai yang berasal dari kedua sisi adalah:

  ${\begin{aligned}\left\{\log(w^{z})\right\}&=\left\{z\cdot \operatorname {Log} (w)+z\cdot 2\pi in+2\pi im\right\}\\\left\{z\cdot \log(w)\right\}&=\left\{z\cdot \operatorname {Log} (w)+z\cdot 2\pi in\right\}\end{aligned}}$

• Identitas (bc)^x = b^xc^x dan (b/c)^x = b^x/c^x adalah absah jika b dan c adalah bilangan real positif dan x adalah bilangan real. Tetapi perhitungan menggunakan cabang utama menunjukkan bahwa
  $1=(-1\cdot -1)^{\frac {1}{2}}\not =(-1)^{\frac {1}{2}}(-1)^{\frac {1}{2}}=-1$

  dan

  $i=(-1)^{\frac {1}{2}}=\left({\frac {1}{-1}}\right)^{\frac {1}{2}}\not ={\frac {1^{\frac {1}{2}}}{(-1)^{\frac {1}{2}}}}={\frac {1}{i}}=-i$

  Di sisi lain, ketika x adalah bilangan bulat, identitas absah-nya untuk semua bilangan kompleks bukan nol.

  Jika eksponensial dianggap sebagai fungsi multinilai maka nilai yang mungkin dari (−1 ⋅ 1)^1/2 adalah {1, −1}. Identitasnya berlaku, tetapi mengatakan {1} = {(−1 ⋅ 1)^1/2} adalah salah.
• Identitas (e^x)^y = e^xy berlaku untuk bilangan real x dan y, tetapi dengan asumsi kebenarannya untuk bilangan kompleks mengarah ke paradoks berikut, ditemukan pada tahun 1827 oleh Clausen: Untuk sembarang bilangan bulat n, memiliki:
  1. $e^{1+2\pi in}=e^{1}e^{2\pi in}=e\cdot 1=e$
  2. $\left(e^{1+2\pi in}\right)^{1+2\pi in}=e\qquad$ (mengambil ke-$(1+2\pi in)$ kuasa kedua sisi)
  3. $e^{1+4\pi in-4\pi ^{2}n^{2}}=e\qquad$ (menggunakan $\left(e^{x}\right)^{y}=e^{xy}$ dan memperluas eksponen)
  4. $e^{1}e^{4\pi in}e^{-4\pi ^{2}n^{2}}=e\qquad$ (menggunakan $e^{x+y}=e^{x}e^{y}$)
  5. $e^{-4\pi ^{2}n^{2}}=1\qquad$ (membagi dengan e)
  tetapi ini salah jika bilangan bulat n adalah bukan nol. Kesalahannya adalah sebagai berikut: menurut definisi, $e^{y}$ adalah notasi untuk $\exp(y),$ fungsi yang sebenarnya, dan $x^{y}$ adalah notasi untuk $\exp(y\log x),$ yang merupakan fungsi multinilai. Jadi notasi ambigunya ketika x = e. Maka, sebelum memperluas eksponen, baris kedua seharusnya

  $\exp \left((1+2\pi in)\log \exp(1+2\pi in)\right)=\exp(1+2\pi in).$

  Oleh karena itu, ketika memperluas eksponen, apabila implisit menduga bahwa $\log \exp z=z$ untuk nilai kompleks z adalah nilai salah, karena logaritma kompleksnya adalah multinilai. Dengan kata lain, identitas salah (e^x)^y = e^xy harus diganti dengan identitas

  $\left(e^{x}\right)^{y}=e^{y\log e^{x}},$

  yang merupakan identitas hakiki antara fungsi multinilai.

Nol pangkat nol

Analisis

Grafik fungsi $z=x^{y}$ untuk $x\in [0,1]$ dan $y\in [-1,+1]$ dengan perhatian khusus pada lingkungan $(0;0;z)$, dimana (vertikal) garis lurus permukaan berakhir. Kurva berwarna menunjukkan perkiraan yang berbeda (0; 0) dengan nilai batas yang berbeda untuk $0^{0}$.

Pertanyaan apakah dan dengan cara apa nilai unik dapat diberikan ke ekspresi $0^{0}$ yang telah dikuasai matematikawan setidaknya sejak paruh pertama abad ke-19.

Gambar yang berdekatan menunjukkan dalam representasi 3D dari graf dari fungsi $z=x^{y}$, bahwa setiap nilai $z\in \mathbb {R} _{\geq 0}$ dengan pilihan titik aproksimasi yang sesuai $(x;y)$ ke asal $(0;0)$ dapat dicapai. Begitu juga

1. $\lim _{y\to 0+}0^{y}=0$,
2. $\lim _{y\to 0+}{\Bigl (}e^{-y^{-2}}{\Bigr )}^{y}=0$,
3. $\lim _{t\to +\infty }x^{y}=c$
   dengan $0<c<1$, $x=c^{t}$ dan $y={\tfrac {1}{t}}$,
4. $\lim _{x\to 0+}x^{0}=1$ dan
5. $\lim _{y\to 0-}{\Bigl (}e^{-y^{-2}}{\Bigr )}^{y}=+\infty$.

Contoh menunjukkan bahwa fungsi $z=x^{y}$ pembagi pada titik $(0;0)$, karena sebuah nilai batas dari tipe $\textstyle \lim _{(x;y)\to (0;0)}\;x^{y}$ tentu saja tidak ada.

Ekspresi bagian bawah ialah tanda nilai batas dan yang tidak dapat dihitung berdasarkan himpunan nilai batas dan sifat kontinuitas yang disebut juga ekspresi tak wajar. Contohnya adalah ${\tfrac {0}{0}},\,{\tfrac {\infty }{\infty }}$ sebagai $0^{0}$. Ekspresi terakhir muncul saat menghitung pangkat basis dan eksponennya mendekati $0$, dan tidak dapat ditentukan jika tidak ada hubungan antara keduanya.

Nilai yang sesuai dalam keadaan yang jelas dapat menjadi urutan $1$ (pada bagian garis lurus $(x;0;1)$, karena $x^{0}=1$ yang berlaku untuk sembarang $x\in \mathbb {R} ^{\times }$) atau urutan $0$ (khusus pada bagian $(0;+y;0)$, karena $0^{y}=0$ berlaku untuk $y\in \mathbb {R} ^{+}$). Es gibt aber auch moderne Analysislehrbücher, die die Potenz $0^{0}$ (in dieser Form) ausdrücklich undefiniert lassen.

Bis Anfang des 19. Jahrhunderts haben Mathematiker anscheinend $0^{0}=1$ gesetzt, ohne diese Festlegung genauer zu hinterfragen. Augustin-Louis Cauchy listete allerdings $0^{0}$ gemeinsam mit anderen Ausdrücken wie $0/0$ in einer Tabelle von unbestimmten Ausdrücken. 1833 veröffentlichte Guillaume Libri eine Arbeit, in der er wenig überzeugende Argumente für $0^{0}=1$ präsentierte, die in der Folge kontrovers diskutiert wurden. Zur Verteidigung von Libri veröffentlichte August Ferdinand Möbius einen Beweis seines Lehrers Johann Friedrich Pfaff, der im Wesentlichen zeigte, dass  $\textstyle \lim _{x\to 0+}x^{x}=1$ gilt, und einen angeblichen Beweis für  $\textstyle \lim _{t\to 0+}x(t)^{y(t)}=1$, falls  $\textstyle \lim _{t\to 0+}x(t)=\lim _{t\to 0+}y(t)=0$ gelten, lieferte. Die Korrektheit dieses Beweises wurde durch das Gegenbeispiel $x(t)=e^{-1/t}$ und $y(t)=t$ rasch widerlegt.

Donald E. Knuth erwähnte 1992 im American Mathematical Monthly die Geschichte der Kontroverse und lehnte die Schlussfolgerung entschieden ab, dass $0^{0}$ undefiniert gelassen wird. Wenn man den Wert 1 für die Potenz $0^{0}$ nicht voraussetzt, verlangen viele mathematische Aussagen wie zum Beispiel der binomische Satz

$(a+b)^{n}=\sum _{k=0}^{n}{n \choose k}a^{k}b^{n-k}$

eine Sonderbehandlung für die Fälle $a=0$ (am Index $k=0$) oder $b=0$ (am Index $k=n$) oder $a+b=0$ (bei $n=0$).

Ebenso kommt die Potenz $0^{0}$ in Potenzreihen wie beispielsweise für die Exponentialfunktion

$e^{t}=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}$

für $t=0$ am Index $n=0$ oder in der Summenformel für die geometrische Reihe

$\sum _{k=0}^{n}q^{k}={\frac {1-q^{n+1}}{1-q}}$

für $q=0$ am Index $k=0$ vor. Auch hier hilft die Konvention $0^{0}=1$.

Die angeführten Anwendungsfälle der Potenz $0^{0}$ sind (wie außerordentlich viele ähnliche andere) Aussagen über Polynome, Multinome oder Potenzreihen, bei denen der Exponent $y$ des Terms $x^{y}$ konstant 0 ist und die Basis $x$ – eher ausnahmsweise – den Wert 0 annehmen kann. In allen diesen Fällen sind die vorkommenden Terme stetige Summanden oder Faktoren, die für invertierbares $x$ den Wert 1 haben, deren Wert dann auch für die Lücke $x\to 0$ mühelos (und ganz im Sinn von $0^{0}=1$) als 1 stetig ergänzt werden kann.

Knuth differenziert jedoch und schreibt: “Cauchy had good reason to consider $0^{0}$ as an undefined limiting form” (deutsch etwa: Cauchy hatte guten Grund, $0^{0}$ als unbestimmten Limes-Ausdruck zu betrachten), wobei er unter der limiting form $0^{0}$ Grenzprozesse der Form $\lim x(t)^{y(t)}$ versteht, bei denen sich sowohl die Basis $x(t)$ wie der Exponent $y(t)$ für ein gewisses $t$ der 0 beliebig nähern.

Mit dieser Maßgabe von D. E. Knuth sind die einfachen Fälle der Absolutglieder in Polynomen und Potenzreihen unmittelbar und pauschal gelöst, ohne dass es zu einem Konflikt mit einer detaillierten Betrachtung komplizierterer Grenzprozesse käme.

Mengenlehre

In der Mengenlehre wird eine Potenz $B^{A}$ zweier Mengen als Menge aller Funktionen von $A$ nach $B$ definiert, das heißt als Menge von Mengen $f$ geordneter Paare $(a,b)$, sodass es zu jedem $a\in A$ genau ein $b\in B$ gibt mit $(a,b)\in f$. Bezeichnet man mit $|A|$ die Mächtigkeit von $A$, so gilt $|B^{A}|=|B|^{|A|}$ (für endliche Mengen, aber auch darüber hinaus), was die Potenzschreibweise für Mengen rechtfertigt. Nun gibt es genau eine auf der leeren Menge $\emptyset$ definierte Funktion, das heißt Menge von Paaren mit obiger Eigenschaft, nämlich $\emptyset$. Daher gilt $B^{\emptyset }=\{\emptyset \}$, was auch für $B=\emptyset$ richtig bleibt.

Die natürlichen Zahlen werden in der Mengenlehre rekursiv wie folgt definiert (siehe von Neumanns Modell der natürlichen Zahlen):

$0:=\emptyset ,\,1:=\{0\}=\{\emptyset \},\,2:=\{0,1\}=\{\emptyset ,\{\emptyset \}\},\,3:=\{0,1,2\}=\dotsb$

Demnach gilt in der Mengenlehre:

$0^{0}=\emptyset ^{\emptyset }=\{\emptyset \}=1$

Eksponen irasional

Artikel utama: Teorema Gelfond–Schneider

Jika b adalah real positif bilangan aljabar, dan x adalah bilangan rasional, telah ditunjukkan di atas bahwa b^x adalah bilangan aljabar. Ini sisa hakiki bahkan apabila jika menerima bilangan aljabar untuk b, dengan satu-satunya perbedaan bahwa b^x mengambil beberapa nilai (bilangan terbatas, lihat di bawah), yang merupakan aljabar. Teorema Gelfond–Schneider diberikan beberapa informasi tentang sifat b^x ketika x adalah irasional (yaitu, bukan rasional). Maka, ini menyatakan:

Jika b adalah bilangan aljabar yang berbeda dari 0 dan 1, dan x adalah bilangan aljabar irasional, maka semua nilai b^x (banyaknya, tak hingga) adalah transendental (bukan aljabar).

Kuasa bilangan bulat dalam aljabar

Definisi eksponen dengan eksponen bilangan bulat positif sebagai perkalian berulang yang berlaku untuk operasi asosiatif apa pun yang dilambangkan sebagai perkalian. Definisi $x^{0}$ memerlukan keberadaan identitas perkalian lebih lanjut.

Sebuah struktur aljabar yang terdiri dari himpunan bersama dengan operasi asosiatif yang dilambangkan dengan perkalian, dan identitas perkalian yang dilambangkan dengan 1 adalah monoid. Dalam monoid, eksponensial elemen x didefinisikan secara induktif oleh

• $x^{0}=1,$
• $x^{n+1}=xx^{n}$ untuk setiap bilangan bulat nonnegatif n.

Jika n adalah bilangan bulat negatif, $x^{n}$ didefinisikan hanya jika x memiliki invers perkalian. Dalam hal ini, invers dari x dinotasikan $x^{-1},$ dan $x^{n}$ didefinisikan sebagai $\left(x^{-1}\right)^{-n}.$

Eksponen dengan eksponen bilangan bulat mematuhi hukum berikut, untuk x dan y dalam struktur aljabar, dan m dan n bilangan bulat:

${\begin{aligned}x^{0}&=1\\x^{m+n}&=x^{m}x^{n}\\(x^{m})^{n}&=x^{mn}\\(xy)^{n}&=x^{n}y^{n}\quad {\text{jika }}xy=yx,{\text{dan, khususnya, jika perkaliannya adalah komutatif.}}\end{aligned}}$

Definisi ini banyak digunakan di banyak bidang matematika, terutama untuk geup, gelanggang, medan, matriks persegi (yang membentuk gelanggang). Mereka berlaku juga untuk fungsi dari himpunan ke diri-sendiri, yang membentuk monoid bawah komposisi fungsi. Ini termasuk, sebagai contoh spesifik, transformasi geometris, dan endomorfisme dari struktur matematika.

Ketika ada beberapa operasi ulangan, adalah umum untuk menunjukkan operasi berulang/ulangan dengan menempatkan simbolnya di superskrip, sebelum eksponen. Misalnya, jika f adalah fungsi real yang nilainya dapat dikalikan, $f^{n}$ menunjukkan eksponensial terhadap perkalian, dan $f^{\circ n}$ ditunjukkan eksponensial sehubungan dengan komposisi fungsi. Yaitu,

$(f^{n})(x)=(f(x))^{n}=f(x)\,f(x)\cdots f(x),$

dan

$(f^{\circ n})(x)=f(f(\cdots f(f(x))\cdots )).$

Biasanya, $(f^{n})(x)$ dinotasikan $f(x)^{n},$ sedangkan $(f^{\circ n})(x)$ dilambangkan $f^{n}(x).$

Dalam sebuah grup

Sebuah grup perkalian adalah himpunan dengan operasi asosiatif dilambangkan sebagai perkalian, yang memiliki elemen identitas, dan setiap elemen memiliki invers.

Jadi, jika G adalah grup, $x^{n}$ didefinisikan untuk setiap $x\in G$ dan setiap bilangan bulat n.

Himpunan dari semua kuasa suatu elemen dari grup membentuk subgrup. Sebuah gruprup (atau subgrup) yang terdiri dari semua kuasa dari elemen tertentu x adalah grup siklik yang dihasilkan oleh x. Jika semua kuasa x berbeda, grupnya adalah isomorfik pada grup aditif $\mathbb {Z}$ dari bilangan bulat. Jika tidak, grup siklik adalah hingga (memiliki jumlah elemen hingga), dan jumlah elemennya adalah urutan dari x. Jika urutan x adalah n, maka $x^{n}=x^{0}=1,$ dan grup siklik yang dihasilkan oleh x terdiri dari n kuasa pertama x (mulai dengan acuh tak acuh dari eksponen 0 atau 1).

Urutan elemen memainkan peran mendasar dalam teori grup. Misalnya, urutan suatu elemen dalam grup hingga selalu merupakan pembagi dari jumlah elemen grup tersebut ("urutan" grup). Kemungkinan urutan elemen grup penting dalam studi struktur grup (lihat teorema Sylow), dan dalam klasifikasi grup sederhana hingga.

Notasi superskrip juga digunakan untuk konjugasi; yaitu, g^h = h⁻¹gh, dimana g dan h adalah elemen dari grup. Notasi ini tidak diubah dengan eksponensial, karena superskrip bukan bilangan bulat. Motivasi dari notasi ini adalah bahwa konjugasi memenuhi beberapa hukum eksponensial, yaitu $(g^{h})^{k}=g^{hk}$ dan $(gh)^{k}=g^{k}h^{k}.$

Dalam sebuah gelanggang

Dalam sebuah gelanggang, bahwa beberapa elemen bukan nol memenuhi $x^{n}=0$ untuk beberapa bilangan bulat n. Unsur tersebut disebut juga nilpoten. Dalam gelanggang komutatif, unsur-unsur nilpoten membentuk ideal, disebut juga nilradikal dari gelanggang.

Jika nilradikal direduksi menjadi ideal nol (yaitu, jika $x\neq 0$ menyatakan $x^{n}\neq 0$ untuk setiap bilangan bulat positif n), ring komutatif dikatakan tereduksi. Gelanggang tereduksi penting dalam geometri aljabar, karena gelanggang koordinat dari himpunan aljabar Affin merupakan gelanggang tereduksi.

Lebih umum, diberikan ideal I dalam gelanggang komutatif R, himpunan elemen R yang memiliki kuasa I adalah ideal, yang disebut radikal dari I. Nilradikal adalah radikal dari zero ideal. Sebuah ideal radikal adalah ideal yang sama dengan radikal-diri. Dalam gelanggang polinomial $k[x_{1},\ldots ,x_{n}]$ atas medan k, sebuah ideal adalah radikal jika dan hanya jika itu adalah himpunan semua polinomial yang nol pada himpunan aljabar affin (ini adalah konsekuensi dari Hilbertscher Nullstellensatz).

Matriks dan operator linear

Jika A adalah matriks bujur sangkar, maka hasil kali A dengan n itu sendiri disebut kuasa matriks. Juga $A^{0}$ didefinisikan sebagai matriks identitas, dan jika A adalah invers, maka $A^{-n}=\left(A^{-1}\right)^{n}$.

Kuasa matriks sering muncul dalam konteks sistem dinamik diskret, dimana matriks A menyatakan transisi dari vektor keadaan x dari beberapa sistem ke keadaan berikutnya Ax dari sistem. Ini adalah interpretasi standar dari rantai Markov, misalnya, apabila $A^{2}x$ adalah status sistem setelah dua langkah waktu, dan seterusnya: maka, $A^{n}x$ adalah status sistem setelah langkah kali n. Matriks kuasa $A^{n}$ adalah matriks transisi antara keadaan sekarang dan keadaan pada langkah kali n ke depan. Jadi menghitung kuasa matriks setara dengan memecahkan evolusi sistem dinamis. Dalam banyak kasus, kuasa matriks dihitung dengan menggunakan nilai eigen dan vektor eigen.

Selain matriks, operator linear yang umum juga merupakan eksponen. Contohnya adalah turunan operator kalkulus, $d/dx$ salah satu operator linear yang melakukan fungsi $f(x)$ untuk menghasilkan fungsi baru, yaitu $(d/dx)f(x)=f'(x)$. Kuasa ke-n dari operator diferensiasi adalah turunan ke-n:

$\left({\frac {d}{dx}}\right)^{n}f(x)={\frac {d^{n}}{dx^{n}}}f(x)=f^{(n)}(x).$

Contoh-contoh ini adalah untuk eksponen diskret dari operator linear, tetapi dalam keadaan juga diinginkan untuk mendefinisikan kuasa dari operator tersebut dengan eksponen kontinu. Ini adalah titik awal dari teori matematika semigrup. Sama seperti kuasa matriks komputasi dengan eksponen diskret memecahkan sistem dinamis diskret, begitu pula kuasa matriks komputasi dengan eksponen kontinu memecahkan sistem dengan dinamika kontinu. Contohnya termasuk pendekatan untuk menyelesaikan persamaan panas, persamaan Schrödinger, persamaan gelombang, dan persamaan diferensial parsial lainnya yang termasuk evolusi waktu. Kasus khusus eksponensial operator turunan ke kuasa non-bilangan bulat disebut turunan pecahan, yang bersama dengan integral pecahan, merupakan operasi dasar dari kalkulus pecahan.

Medan hingga

Artikel utama: Medan hingga

Sebuah medan adalah struktur aljabar dimana perkalian, penambahan, pengurangan, dan pembagian didefinisikan dan memenuhi sifat-sifatnya yang sudah dikenal; khususnya, perkaliannya adalah asosiatif, dan setiap elemen bukan nol memiliki perkalian invers. Ini menyatakan bahwa eksponen dengan eksponen bilangan bulat didefinisikan dengan baik, kecuali untuk kuasa nonpositif 0. Contoh umum adalah bilangan kompleks dan submedan, bilangan rasional dan bilangan real yang telah dibahas sebelumnya dalam artikel ini, dan semua tak hingga.

Sebuah medan hingga adalah medan dengan elemen bilangan hingga. Jumlah elemen ini adalah bilangan prima atau kuasa prima; yaitu, memiliki bentuk $q=p^{k},$ dimana p adalah bilangan prima, dan k adalah bilangan bulat positif. Untuk setiap q tersebut, ada medan dengan elemen q. Medan dengan elemen q semuanya adalah isomorfik, yang memungkinkan, bekerja seolah-olah hanya ada satu medan dengan elemen q, dilambangkan $\mathbb {F} _{q}.$

Satu-satunya adalah

$x^{q}=x$

untuk setiap $x\in \mathbb {F} _{q}.$

Sebuah elemen primitif di $\mathbb {F} _{q}$ adalah elemen g seperti pada himpunan q − 1 kuasa pertama g (yaitu, $\{g^{1}=g,g^{2},\ldots ,g^{p-1}=g^{0}=1\}$) sama dengan himpunan elemen bukan nol dari $\mathbb {F} _{q}.$ Ada $\varphi (p-1)$ elemen primitif dalam $\mathbb {F} _{q},$ dimana $\varphi$ adalah fungsi totient Euler.

Dalam $\mathbb {F} _{q},$ identitas impian Fresman

$(x+y)^{p}=x^{p}+y^{p}$

adalah hakiki untuk eksponen p. Seperti $x^{p}=x$ di peta $\mathbb {F} _{q},$ maka

${\begin{aligned}F\colon {}&\mathbb {F} _{q}\to \mathbb {F} _{q}\\&x\mapsto x^{p}\end{aligned}}$

adalah linear atas $\mathbb {F} _{q},$ dan merupakan automorfisme medan, disebut automorfisme Frobenius. Jika $q=p^{k},$ medan $\mathbb {F} _{q}$ memiliki k automorfisme, yang merupakan kuasa pertama k (antara komposisi) dari F. Dengan kata lain, grup Galois dari $\mathbb {F} _{q}$ adalah siklik urutan k, yang dihasilkan oleh automorfisme Frobenius.

Pertukaran kunci Diffie–Hellman adalah aplikasi eksponensial dalam Medan hingga yang banyak digunakan untuk komunikasi aman. Ini menggunakan fakta bahwa eksponensial secara komputasi tidak mahal, sedangkan operasi kebalikannya, logaritma diskret, secara komputasi mahal. Lebih tepatnya, jika g adalah elemen primitif dalam $\mathbb {F} _{q},$ maka $g^{e}$ dihitung secara efisien dengan eksponensial dari kuadrat untuk e, bahkan jika q besar, sementara tidak ada algoritma yang diketahui memungkinkan pengambilan e dari $g^{e}$ jika nilai q adalah besar.

Atas himpunan

Artikel utama: Darab Kartesius

Jika n adalah bilangan asli, dan A adalah himpunan sembarang, maka ekspresi Aⁿ sering digunakan untuk menyatakan himpunan dari rangkap-n elemen A. Apabila ditulis Aⁿ menyatakan himpunan fungsi dari himpunan {0, 1, 2, ..., n − 1} ke himpunan A; rangkap-n (a₀, a₁, a₂ , ..., a_n−1) mewakili fungsi i ke a_i.

Untuk bilangan kardinal tak hingga dan himpunan A, notasi A^κ juga digunakan untuk menyatakan himpunan semua fungsi dari himpunan ukuran hingga A. Ini terkadang ditulis ^κA untuk membedakannya dari eksponensial utama, yang didefinisikan di bawah ini.

Eksponensial umum ini juga didefinisikan untuk operasi pada himpunan atau untuk himpunan dengan struktur tambahan. Misalnya, dalam aljabar linear, untuk indeks jumlah langsung dari ruang vektor melalui himpunan indeks arbitrer. Artinya, apabila berbicara tentang

$\bigoplus _{i\in \mathbb {N} }V_{i},$

dimana setiap V_i adalah ruang vektor.

Kemudian jika V_i = V untuk setiap i, jumlah langsung yang dihasilkan ditulis dalam notasi eksponensial sebagai V^⊕N, atau cukup V^N dengan pengertian bahwa jumlah langsung adalah bawaan. Maka, ini bisa diganti kembali himpunan N dengan bilangan kardinal n untuk mendapatkan Vⁿ, meskipun tanpa memilih himpunan standar tertentu dengan kardinalitas n, yang didefinisikan isomorfisme hingga saja. Diberikan V sebagai medan-R dari bilangan real (yang sebagai ruang vektor atas) dan n menjadi beberapa bilangan asli, maka, ini mendapatkan ruang vektor umum yang dipelajari dalam aljabar linear, dan ruang vektor real-Rⁿ.

Jika basis operasi eksponensial adalah himpunan, operasi eksponensial adalah darab Kartesius kecuali dinyatakan yang lain. Karena beberapa darab Cartesian menghasilkan rangkap-n, yang diwakili oleh suatu fungsi pada himpunan kardinalitas yang sesuai, S^N sebagai himpunan semua fungsi dari N hingga S dalam kasus ini:

$S^{N}\equiv \{f\colon N\to S\}.$

Ini cocok dengan eksponen bilangan kardinal, dalam arti bahwa |S^N| = |S|^|N|, dimana |X| adalah kardinalitas X. Ketika "2" didefinisikan sebagai {0, 1}, maka memiliki |2^X| = 2^|X|, dimana 2^X, biasanya dilambangkan dengan P(X), adalah himpunan kuasa dari X; masing-masing himpunan bagian Y dari X berkorespondensi secara unik dengan fungsi pada X yang mengambil nilai 1 untuk x ∈ Y dan 0 untuk x ∉ Y.

Dalam teori kategori

Artikel utama: Kategori tertutup Kartesius

Dalam kategori tertutup Kartesius, operasi eksponensial digunakan untuk kenaikkan objek arbitrer ke kuasa objek lain. Ini menggeneralisasi darab Kartesius dalam kategori himpunan. Jika 0 adalah objek awal dalam kategori tertutup Kartesius, maka objek eksponensial 0⁰ adalah isomorfik ke objek terminal 1.

Dari bilangan kardinal dan ordinal

Artikel utama: Aritmetika kardinal dan Aritmatika ordinal

Dalam teori himpunan, ada operasi eksponensial untuk kardinal dan bilangan ordinal.

Jika κ dan λ adalah bilangan kardinal, ekspresi κ^λ mewakili kardinalitas himpunan fungsi dari sembarang himpunan kardinalitas λ ke himpunan kardinalitas κ. Jika κ dan λ adalah hingga, maka ini sesuai dengan operasi eksponensial aritmetika biasa. Misalnya, himpunan rangkap-3 elemen dari himpunan elemen-2 memiliki kardinalitas 8 = 2³. Dalam aritmetika kardinal, κ⁰ adalah 1 (bahkan jika κ adalah kardinal tak hingga atau nol).

Eksponen bilangan kardinal berbeda dari eksponensial bilangan kardinal, yang didefinisikan oleh proses batas yang melibatkan induksi transfinit.

Eksponensial berulang

Artikel utama: Tetrasi dan Hiperoperasi

Sama seperti eksponensial bilangan asli dimotivasi oleh perkalian berulang, adalah mendefinisikan operasi berdasarkan eksponensial berulang; operasi ini terkadang disebut hiper-4 atau tetrasi. Tetrasi-iterasi mengarah ke operasi lain, dan seterusnya, sebuah konsep bernama hiperoperasi. Urutan operasi ini dinyatakan oleh fungsi Ackermann dan notasi panah atas Knuth. Sama seperti eksponensial pertumbuhan cepat daripada perkalian, pertumbuhan cepat dari penambahan, tetrasi adalah pertumbuhan cepat dari eksponensial. Dinilai pada (3, 3), fungsi penjumlahan, perkalian, eksponensial, dan tetrasi menghasilkan 6, 9, 27, dan 7.625.597.484.987 masing-masing pada (= 3²⁷ = 3³³ = ³3).

Limit kuasa

Nol untuk kuasa nol memberikan sejumlah contoh limit yang berbentuk bentuk tak tentu 0⁰. Limit dalam contoh ini ada, tetapi memiliki nilai yang berbeda, menunjukkan bahwa fungsi dua variabel x^y tidak memiliki limit pada titik (0, 0). Apabila mempertimbangkan pada titik mana fungsi ini memiliki limit.

Lebih tepatnya, perhatikan fungsi f(x, y) = x^y didefinisikan pada D = {(x, y) ∈ R² : x > 0}. Kemudian D dilihat sebagai himpunan bagian dari R² (yaitu, himpunan semua pasangan (x, y) dengan x, y memiliki garis bilangan real diperluas R = [−∞, +∞], dengan darab topologi), yang berisi titik-titik dimana fungsi f memiliki limit.

Faktanya, f memiliki limit di semua titik akumulasi dari D, kecuali (0, 0), (+∞, 0), (1, +∞) dan (1, −∞). Dengan demikian, apabila ini untuk mendefinisikan kuasa x^y dengan kontinuitas 0 ≤ x ≤ +∞, −∞ ≤ y ≤ +∞, kecuali untuk 0⁰, (+∞)⁰, 1^+∞ dan 1^−∞, yang tetap bentuk tak tentu.

Dibawah definisi ini dengan kontinuitas, maka memperoleh:

• x^+∞ = +∞ dan x^−∞ = 0, bila 1 < x ≤ +∞.
• x^+∞ = 0 dan x^−∞ = +∞, bila 0 ≤ x < 1.
• 0^y = 0 dan (+∞)^y = +∞, bila 0 < y ≤ +∞.
• 0^y = +∞ dan (+∞)^y = 0, bila −∞ ≤ y < 0.

Kuasa ini diperoleh dengan mengambil limit x^y untuk nilai positif dari x. Metode ini tidak mengizinkan definisi x^y ketika x < 0, karena pasangan (x, y) dengan x < 0 bukan merupakan titik akumulasi dari D.

Disisi lain, ketika n adalah bilangan bulat, maka kuasa xⁿ bermakna untuk semua nilai x, termasuk yang negatif. Maka, ini membuat definisi 0ⁿ = +∞ yang diperoleh diatas untuk n negatif menjadi bermasalah ketika nilainya adalah n, karena dalam kasus ini xⁿ → +∞ karena x cenderung 0 melalui nilai positif, tetapi bukan nilai negatif.

Komputasi yang efisien dengan eksponen bilangan bulat

Komputasi bⁿ menggunakan perkalian berulang membutuhkan n − 1 operasi perkalian, tetapi itu dapat dihitung lebih efisien dari itu, seperti yang diilustrasikan oleh contoh berikut. Untuk menghitung 2¹⁰⁰, terapkan kaidah Horner ke eksponen 100 yang ditulis dalam biner:

$100=2^{2}+2^{5}+2^{6}=2^{2}(1+2^{3}(1+2))$.

Kemudian hitung suku-suku berikut secara berurutan, baca kaidah Horner dari kanan ke kiri.

22 = 4

2 (22) = 23 = 8

(23)2 = 26 = 64

(26)2 = 212 = 4096

(212)2 = 224 = 16.777.216

2 (224) = 225 = 33.554.432

(225) 2 2 = 250 = 1.125.899.906.842.624

(225)2 = 2100 = 1.267.650.600.228.229.401.496.703.205.376

Rangkaian langkah ini hanya membutuhkan 8 perkalian, bukan 99.

Secara umum, jumlah operasi perkalian yang diperlukan untuk menghitung bⁿ dikurangi menjadi $\sharp n+\lfloor \log _{2}n\rfloor -1,$ dengan menggunakan kuasa dengan kuadrat, dimana $\sharp n$ menunjukkan jumlah 1 dalam wakilan biner dari n. Untuk beberapa eksponen (100 tidak termasuk di antaranya), jumlah perkalian dikurangi lebih lanjut dengan menghitung dan menggunakan kuasa kaidah-tambahan minimal. Menemukan barisan perkalian minimal (kaidah penambahan panjang minimal untuk eksponen) untuk bⁿ adalah soal yang sulit, yang saat ini tidak ada algoritma efisien yang diketahui (lihat Masalah jumlah himpunan bagian), tetapi banyak algoritma heuristik yang cukup efisien tersedia. Namun, dalam perhitungan praktis, eksponensial dengan mengkuadratkan cukup efisien, dan jauh lebih mudah diimplementasikan.

Fungsi teriterasi

Komposisi fungsi adalah operasi biner yang didefinisikan pada fungsi sehingga kodomain dari fungsi yang ditulis sebelah kanan termasuk dalam domain dari fungsi yang ditulis sebelah kiri. Ini dilambangkan $g\circ f,$ dan didefinisikan sebagai

$(g\circ f)(x)=g(f(x))$

untuk setiap x dalam domain f.

Jika domain suatu fungsi f sama dengan kodomainnya, maka ia menyusun fungsi dengan sendiri dalam jumlah waktu yang berubah-ubah, dan ini mendefinisikan kuasa ke-n dari fungsi di bawah komposisi, biasanya disebut iterasi ke-n dari fungsi tersebut. Jadi $f^{n}$ secara umum menunjukkan iterasi ke-n dari f; misalnya, $f^{3}(x)$ berarti $f(f(f(x))).$

Ketika perkalian didefinisikan pada kodomain fungsi, ini mendefinisikan perkalian pada fungsi, perkalian sesetitik, yang menginduksi eksponensial lain. Saat menggunakan notasi fungsional, dua jenis eksponensial umumnya dibedakan dengan menempatkan eksponen dari iterasi fungsional sebelum tanda kurung yang melampirkan argumen fungsi, dan menempatkan eksponen perkalian sesetitik setelah tanda kurung. Jadi $f^{2}(x)=f(f(x)),$ dan $f(x)^{2}=f(x)\cdot f(x).$ Ketika notasi fungsional tidak digunakan, disambiguasi yang dilakukan dengan menempatkan simbol komposisi sebelum eksponen; misalnya $f^{\circ 3}=f\circ f\circ f,$ dan $f^{3}=f\cdot f\cdot f.$ Untuk alasan historis, eksponen dari perkalian berulang ditempatkan sebelum argumen untuk beberapa fungsi tertentu, biasanya fungsi trigonometri. Jadi, $\sin ^{2}x$ dan $\sin ^{2}(x)$ berarti keduanya $\sin(x)\cdot \sin(x)$ dan bukan $\sin(\sin(x)),$ yang jarang dipertimbangkan. Secara historis, beberapa varian notasi ini digunakan oleh penulis yang berbeda.

Dalam konteks ini, eksponen $-1$ selalu menunjukkan fungsi invers, jika ada. Jadi $\sin ^{-1}x=\sin ^{-1}(x)=\arcsin x.$ Untuk pecahan perkalian invers umumnya digunakan seperti pada $1/\sin(x)={\frac {1}{\sin x}}.$

Dalam bahasa pemrograman

Bahasa pemrograman umumnya menyatakan eksponensial baik sebagai operator infiks atau sebagai fungsi (awalan), karena mereka adalah notasi linear yang tidak mendukung superskrip:

• x ↑ y: Algol, Komodor BASIC, TRS-80 Level II/III BASIC.
• x ^ y: AWK, BASIC, J, MATLAB, Wolfram Language (Mathematica), R, Microsoft Excel, Analytica, TeX (dan turunannya), TI-BASIC, bc (untuk eksponen bilangan bulat), Haskell (untuk eksponen bilangan bulat nonnegatif), Lua dan sebagian besar sistem aljabar komputer. Penggunaan simbol ^ yang bertentangan meliputi: XOR (dalam ekspansi aritmetika POSIX Shell, AWK, C, C++, C#, D, Go, Java, JavaScript, Perl, PHP, Python, Ruby dan Tcl), Indirection (Pascal), dan rangkaian string (OCaml dan Standard ML).
• x ^^ y: Haskell (untuk basis pecahan, eksponen bilangan bulat), D.
• x ** y: Ada, Z shell, KornShell, Bash, COBOL, CoffeeScript, Fortran, FoxPro, Gnuplot, Groovy, JavaScript, OCaml, F#, Perl, PHP, PL/I, Python, Rexx, Ruby, SAS, Seed7, Tcl, ABAP, Mercury, Haskell (untuk eksponen floating-point), Turing, VHDL.
• pown x y: F# (for integer base, integer exponent).
• x⋆y: APL.

Many other programming languages lack syntactic support for exponentiation, but provide library functions:

• pow(x, y): C, C++.
• Math.Pow(x, y): C#.
• math:pow(X, Y): Erlang.
• Math.pow(x, y): Java.
• [Math]::Pow(x, y): PowerShell.
• (expt x y): Common Lisp.

Untuk eksponen tertentu ada cara khusus untuk menghitung x^y jauh lebih cepat daripada melalui eksponen umum. Kasus ini mencakup bilangan bulat positif dan negatif kecil (memilih x · x daripada x²; memilih 1/x daripada x⁻¹) dan root (memilih sqrt(x) daripada x^0.5, memilih cbrt(x) daripada x^{1/3</ sup>).}

Tidak semua bahasa pemrograman menggunakan konvensi asosiasi yang sama untuk eksponensial: sedangkan Wolfram Language, Google Penelusuran dan lainnya menggunakan pengaitan kanan (yaitu a^b^c dievaluasi sebagai a^(b^c)), banyak program komputer seperti Microsoft Office Excel dan Matlab mengasosiasikan ke kiri (yaitu a^b^c dievaluasi sebagai (a^b)^c).

Lihat pula

• Fungsi eksponensial ganda
• Peluruhan eksponensial
• Medan eksponensial
• Pertumbuhan eksponensial
• Daftar topik eksponensial
• Eksponensial modular
• Notasi ilmiah
• Subskrip dan superskrip Unicode
• x^y = y^x
• Nol untuk kuasa nol